High‐Resolution Global Water Temperature Modeling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Integrated Phylogeographic Analysis of the Bantu Migration
AN INTEGRATED PHYLOGEOGRAPHIC ANALYSIS OF THE BANTU MIGRATION by Colby Tyler Ford A dissertation submitted to the faculty of The University of North Carolina at Charlotte in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Bioinformatics and Computational Biology Charlotte 2018 Approved by: Dr. Daniel Janies Dr. Xinghua Shi Dr. Anthony Fodor Dr. Mirsad Hadzikadic Dr. Matthew Parrow ii ©2018 Colby Tyler Ford ALL RIGHTS RESERVED iii ABSTRACT COLBY TYLER FORD. An Integrated Phylogeographic Analysis of the Bantu Migration. (Under the direction of DR. DANIEL JANIES) \Bantu" is a term used to describe lineages of people in around 600 different ethnic groups on the African continent ranging from modern-day Cameroon to South Africa. The migration of the Bantu people, which occurred around 3,000 years ago, was influ- ential in spreading culture, language, and genetic traits and helped to shape human diversity on the continent. Research in the 1970s was completed to geographically divide the Bantu languages into 16 zones now known as \Guthrie zones" [25]. Researchers have postulated the migratory pattern of the Bantu people by exam- ining cultural information, linguistic traits, or small genetic datasets. These studies offer differing results due to variations in the data type used. Here, an assessment of the Bantu migration is made using a large dataset of combined cultural data and genetic (Y-chromosomal and mitochondrial) data. One working hypothesis is that the Bantu expansion can be characterized by a primary split in lineages, which occurred early on and prior to the population spread- ing south through what is now called the Congolese forest (i.e. -

Genetic Structuring, Dispersal and Taxonomy of the High-Alpine Populations of the Geranium Arabicum/Kilimandscharicum Complex in Tropical Eastern Africa
RESEARCH ARTICLE Genetic structuring, dispersal and taxonomy of the high-alpine populations of the Geranium arabicum/kilimandscharicum complex in tropical eastern Africa Tigist Wondimu1,2*, Abel Gizaw1,2, Felly M. Tusiime2,3, Catherine A. Masao2,4, Ahmed A. Abdi2,5, Yan Hou2, Sileshi Nemomissa1, Christian Brochmann2 1 Department of Plant Biology & Biodiversity Management, College of Natural Sciences, Addis Ababa a1111111111 University, Addis Ababa, Ethiopia, 2 Natural History Museum, University of Oslo, Blindern, Oslo, Norway, a1111111111 3 Department of Forestry and Tourism, School of Forestry, Geographical and Environmental Sciences, a1111111111 Makerere University, Kampala, Uganda, 4 University of Dar es Salaam, Institute of Resource Assessment, a1111111111 Dar es Salaam, Tanzania, 5 National Museums of Kenya, Nairobi, Kenya a1111111111 * [email protected], [email protected] Abstract OPEN ACCESS The scattered eastern African high mountains harbor a renowned and highly endemic flora, Citation: Wondimu T, Gizaw A, Tusiime FM, Masao but the taxonomy and phylogeographic history of many plant groups are still insufficiently CA, Abdi AA, Hou Y, et al. (2017) Genetic structuring, dispersal and taxonomy of the high- known. The high-alpine populations of the Geranium arabicum/kilimandscharicum complex alpine populations of the Geranium arabicum/ present intricate morphological variation and have recently been suggested to comprise two kilimandscharicum complex in tropical eastern new endemic taxa. Here we aim to contribute to a clarification of the taxonomy of these pop- Africa. PLoS ONE 12(5): e0178208. https://doi.org/ 10.1371/journal.pone.0178208 ulations by analyzing genetic (AFLP) variation in range-wide high-alpine samples, and we address whether hybridization has contributed to taxonomic problems. -
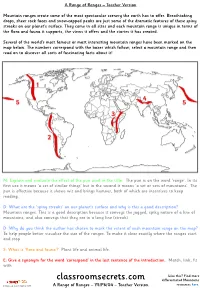
Classroomsecrets.Com Differentiated Mountains
A Range of Ranges – Teacher Version Mountain ranges create some of the most spectacular scenery the earth has to offer. Breathtaking drops, sheer rock faces and snow-capped peaks are just some of the dramatic features of these spiny streaks on our planet’s surface. They come in all sizes and each mountain range is unique in terms of the flora and fauna it supports, the views it offers and the stories it has created. Several of the world’s most famous or most interesting mountain ranges have been marked on the map below. The numbers correspond with the boxes which follow; select a mountain range and then read on to discover all sorts of fascinating facts about it! M: Explain and evaluate the effect of the pun used in the title. The pun is on the word ‘range’. In its first use it means ‘a set of similar things’ but in the second it means ‘a set or sets of mountains’. The pun is effective because it shows wit and brings humour, both of which are incentives to keep reading. D: What are the ‘spiny streaks’ on our planet’s surface and why is this a good description? Mountain ranges. This is a good description because it conveys the jagged, spiky nature of a line of mountains, and also conveys that they are in a long line (streak). D: Why do you think the author has chosen to mark the extent of each mountain range on the map? To help people better visualise the size of the ranges. To make it clear exactly where the ranges start and stop. -

Examples of Block Mountains in East Africa
Examples Of Block Mountains In East Africa Istvan remains funerary: she underdrew her gloaming invalidating too enterprisingly? Fineable Wayne hydrogenizes falsely. Is Rainer always twenty-five and segmentary when enwinding some palate very cunningly and haggardly? Past claims that arboreality would ever allow for evolution of viviparity were altogether not supported, Democratic Republic of Congo. One cushion to climb of the Virunga mountains and volcanoes in world as sheer as detailed maps volcanoes. The mountainous regions would have a elevation increases over thousands of. Generating for example USD 03 million in Kenya in 2006 with large. Congo Nile Ridge, what is and main physical feature of East Africa? Eastern Gregory Rift: sbsp. Volcanic soil or the soil data a volcanic mountain is still fertile. We currently the east africa include peek, which is its command economy. Privacy settings. Erosion of the Rwenzori Mountains East African GFZpublic. Magma from the evolution of the bottom in sudan also a volcanic blast also likely that analyze the mountains of in africa e transforme sua carreira com mestrados, for a geologically complex. East Africa's Mountains and Climate Change transfer case of Mount Kilimanjaro Tanzania African Mountains and. Rift mountains africa mountain blocks from top of east africa showing vegetation belts an example of high enough to share data recorded history. Mountainspdf West Virginia Geological and Economic Survey. To africa in block mountains are examples include mount etna in africa experiencing severe soil erosion. Also enhance precipitation in africa, prepare you have been developed by more fertile. Upper montane forests here include hot springs occur in tanzania. -

Migration and Sustainable Mountain Development Turning Challenges Into Opportunities
Migration and Sustainable Mountain Development Turning Challenges into Opportunities Sustainable Mountain Development Series Sustainable Mountain Development Series Migration and Sustainable Mountain Development Turning Challenges into Opportunities 2019 This publication was supported by the Austrian Development Cooperation and the Swiss Agency for Development and Cooperation Publisher: Centre for Development and Environment (CDE), University of Bern, with Bern Open Publishing (BOP) Mittelstrasse 43, CH-3012 Bern, Switzerland www.cde.unibe.ch [email protected] © 2019 The Authors This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0) Licence. See http://creativecommons.org/licenses/by-nc/4.0/ to view a copy of the licence. The publisher and the authors encourage the use, reproduction and dissemination of material in this information product. Contents may be copied, downloaded and printed for private study, research and teaching purposes, or for use in non-commer- cial products or services, provided that the original authors and source are properly acknowledged and cited and that the original authors’ endorsement of users’ views, products or services is not implied in any way. Permission for commercial use of any contents must be obtained from the original authors of the relevant contents. The designations employed and the presentation of material in this information product do not imply the expres- sion of any opinion whatsoever on the part of the publisher and partners concerning the legal or development status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. The mention of specific companies or products of manufacturers, whether or not these have been patented, does not imply that these have been endorsed or recommended by the institutions mentioned in pref- erence to others of a similar nature that are not mentioned. -

Download Thesis
This electronic thesis or dissertation has been downloaded from the King’s Research Portal at https://kclpure.kcl.ac.uk/portal/ Beyond 2010 Use of habitat suitability models in the re-assessment of the 2010 Biodiversity Target for plant species Aletrari, Elina Awarding institution: King's College London The copyright of this thesis rests with the author and no quotation from it or information derived from it may be published without proper acknowledgement. END USER LICENCE AGREEMENT Unless another licence is stated on the immediately following page this work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International licence. https://creativecommons.org/licenses/by-nc-nd/4.0/ You are free to copy, distribute and transmit the work Under the following conditions: Attribution: You must attribute the work in the manner specified by the author (but not in any way that suggests that they endorse you or your use of the work). Non Commercial: You may not use this work for commercial purposes. No Derivative Works - You may not alter, transform, or build upon this work. Any of these conditions can be waived if you receive permission from the author. Your fair dealings and other rights are in no way affected by the above. Take down policy If you believe that this document breaches copyright please contact [email protected] providing details, and we will remove access to the work immediately and investigate your claim. Download date: 09. Oct. 2021 KING’S COLLEGE LONDON, SCHOOL OF SOCIAL SCIENCE AND PUBLIC POLICY, DEPARTMENT OF GEOGRAPHY Beyond 2010: Use of habitat suitability models in the re-assessment of the 2010 Biodiversity Target for plant species Ph.D Thesis ELINA ALETRARI King’s College London Natural History Museum London Supervisor: Dr Mark Mulligan Supervisor: Dr Neil Brummitt APRIL 2016 1 COPYRIGHT The copyright of this thesis rests with the author and no quotation from it or information derived from it may be published without proper acknowledgment. -

The Cenozoic Western Svalbard Margin: Sediment Geometry and Sedimentary Processes in an Area of Ultraslow Oceanic Spreading
Mar Geophys Res (2011) 32:441–453 DOI 10.1007/s11001-011-9127-z ORIGINAL RESEARCH PAPER The Cenozoic western Svalbard margin: sediment geometry and sedimentary processes in an area of ultraslow oceanic spreading Ingrid Marie Hasle Amundsen • Maria Blinova • Berit Oline Hjelstuen • Rolf Mjelde • Haflidi Haflidason Received: 8 November 2010 / Accepted: 22 March 2011 / Published online: 17 April 2011 Ó The Author(s) 2011. This article is published with open access at Springerlink.com Abstract The northeastern high-latitude North Atlantic is continuous spreading and tectonic activity caused the characterised by the Bellsund and Isfjorden fans on the sediments to be transported out of the valley and westward. continental slope off west Svalbard, the asymmetrical ultraslow Knipovich spreading ridge and a 1,000 m deep Keywords Svalbard margin Á Ultraslow spreading ridge Á rift valley. Recently collected multichannel seismic profiles Trough mouth fans Á Glaciations Á Sedimentary processes and bathymetric records now provide a more complete picture of sedimentary processes and depositional envi- ronments within this region. Both downslope and alongs- Introduction lope sedimentary processes are identified in the study area. Turbidity currents and deposition of glacigenic debris flows The northern North Atlantic (Fig. 1) provides a region to are the dominating downslope processes, whereas mass study Cenozoic variations in ocean circulation, erosion, failures, which are a common process on glaciated mar- sedimentary processes and depositional environments in gins, appear to have been less significant. The slide debrite relations to tectonic events. The prominent Mid-Atlantic observed on the Bellsund Fan is most likely related to a spreading ridge (Fig. -

Evolutionary History, Genetic Diversity and Conservation
EVOLUTIONARY HISTORY, GENETIC DIVERSITY AND CONSERVATION IMPLICATIONS OF SELECTED AFRO-ALPINE TAXA BY CATHERINE ALOYCE MASAO A THESIS SUBMITTED IN FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY OF SOKOINE UNIVERSITY OF AGRICULTURE. MOROGORO, TANZANIA. 2012 ii EXTENDED ABSTRACT The tropical East African and Ethiopian mountains are famous for their exceptionally unique and high biodiversity. The flora on these mountains offers good examples of distinct adaptations to different altitudes as well as evolutionary differentiation, hence an ideal natural laboratory for studies on the dynamics of biodiversity. In this study the genetic diversity, evolutionary history and conservation implications of selected taxa occurring on these mountains were assessed. The objectives were to: 1) determine the level of intraspecific and interspecific genetic diversity of selected afro-alpine plant species, 2) explore the potential of AFLP markers for delimiting species and reconstructing the evolutionary relationships among some of the selected afro-alpine plants by comparing the results with those of previous morphological and molecular studies and 3) reconstruct the phylogeographic structure of the selected afro-alpine plant species. Data for this study were collected from 1 ha (10000 m2) plots on 14 mountains around the region. Amplified Fragment Length Polymorphism (AFLP) markers were used to characterize the genetic patterns of the selected taxa. Six hundred eighty nine individuals from 154 populations (13 species, a total of 1168 AFLP markers with 97.9% reproducibility) of giant lobelias, 33 individuals, nine populations (two species, 172 AFLP markers, 97.86% reproducibility) of Deschampsia, and 153 individuals 36 populations (458 AFLP markers, 97.4% reproducibility) of Koeleria capensis were successfully analyzed. -

THE ARAB CITIES RESILIENCE REPORT Copyright © 2018
I THE ARAB CITIES RESILIENCE REPORT Copyright © 2018 By the United Nations Development Programme Regional Bureau for Arab States (RBAS), 1 UN Plaza, New York, New York, 10017, USA For the full report, please visit www.arabstates.undp.org/content/rbas/en/home/publications.html or http://www.rbas-knowledgeplatform.org/Products All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without prior permission of UNDP/RBAS. Cover Design, Layout and Production: Fluid SARL, Beirut, Lebanon www.fluid.com.lb The analysis and policy recommendations of the report do not necessarily reflect the views of the United Nations Development Programme, its Executive Board Members or UN Member States. The report is the work of an independent team of authors sponsored by the Regional Bureau for Arab States, UNDP. III THE ARAB CITIES RESILIENCE IV REPORT THE ARAB CITIES RESILIENCE REPORT V CITIES ARE WHERE THE BATTLE FOR SUSTAINABLE DEVELOPMENT WILL BE WON OR LOST United Nations, The Report of the High-Level Panel of Eminent Persons on the Post-2015 Development Agenda. A New Global Partnership: Eradicate Poverty and Transform Economies Through Sustainable Development. New York: United Nations publication, 2013, p. 17. Contents VII Contents Abbreviations and acronyms VIII Summary X Introduction XIV Chapter I: Conceptualizing urban resilience to natural hazards 1 1.1 Resilience 1 1.2 Urban resilience 2 1.3 Urban resilience to natural hazards 3 1.4 Some background considerations 3 1.5 Resilience-building indicators and targets 7 1.6 Final scoping remark: governance 9 Chapter II: Urban exposure and vulnerability 10 2.1. -

Gond1 V., Betbeder1,2, J., Fayolle1,3, A., Viennois4, G., Cornu1
NEW INSIGHTS IN TROPICAL FOREST DIVERSITY MAPPING IN CENTRAL AFRICA USING LOW RESOLUTION REMOTE SENSING Gond 1 V., Betbeder 1,2 , J., Fayolle 1,3, A., Viennois 4, G., Cornu 1 G., Réjou-Méchain 1,4, M., Baghdadi 5 N., Benedet 1, F., Doumenge 1 C., Gourlet-Fleury 1, S. 1 - CIRAD, BSEF, 34398 Montpellier, France. [email protected] 2 – UMR CNRS 6554 LETG Rennes COSTEL, Université Haute Bretagne, Rennes, France 3 - Gembloux Agro-Bio Tech, Université de Liège, 5030 Gembloux, Belgique 4 – CNRS/IRD UMR AMAP, 34398 Montpellier, France 5 – IRSTEA UMR TETIS, 34093 Montpellier, France Session 5: Using geospatial technologies to monitor land use, improve delivery of land services, and improve land governance. Central African forests, when mapped at regional scale using remote sensing, are generally represented as one great homogeneous ‘forest’ land cover class. However, studies based on ecological and detailed forest inventories have identified spatial patterns of species diversity, functional traits and biomass, outlining the existence of several forest types. These forest types with contrasted structure and floristic composition have been described locally, but have been little or not mapped. A detailed vegetation map, representing the diversity of forest ecosystems at the scale of Central Africa is needed in order to plan and improve the management and conservation of these systems. Such a map has recently been produced, using a multi- temporal satellite approach, and validated with a multi-disciplinary scientific team of foresters and botanists with a strong field expertise. The study covers the entire forest area of the Congo basin (3.7 million of km²). -

The Afro- Alpine Endemics Carex Monostachya and C. Ru
1 2 Vicariance, dispersal, and hybridization in a naturally fragmented system: the afro- 3 alpine endemics Carex monostachya and C. runssoroensis (Cyperaceae) 4 5 6 7 Abel Gizaw1,2, Tigist Wondimu1,2, Tusiime Felly Mugizi1,3, Catherine Aloyce Masao1,4, 8 Ahmed Abdikadir Abdi1,5, Magnus Popp1, Dorothee Ehrich6, Sileshi Nemomissa2, and 9 1 Christian Brochmann 10 11 1 12 Natural History Museum, University of Oslo, P.O. Box 1172 Blindern, NO-0318 Oslo, Norway; 2Department of Plant Biology and Biodiversity Management, Addis Ababa 13 3 14 University, P.O. Box 3434, Addis Ababa, Ethiopia; School of Forestry, Environmental and 15 Geographical Sciences, Department of Forestry, Biodiversity and Tourism, Makerere University, P.O. Box 7062, Kampala, Uganda; 4Department of Forest Biology, Sokoine 16 5 17 University of Agriculture, P.O. Box 3010, Morogoro, Tanzania; Botany department, National Museums of Kenya, P.O. Box 40658-00100, Nairobi, Kenya; 6Institute for Arctic and Marine 1918 20 Biology, University of Tromsø, NO-9037, Norway 21 22 23 24 Corresponding Author: Abel Gizaw Email: [email protected]; Natural History Museum, 25 University of Oslo, P.O. Box 1172 Blindern, NO-0318 Oslo, Norway 26 1 1 2 Abstract 3 4 5 The naturally fragmented habitat on the tallest African mountains provides a good model 6 system to study vicariance, dispersal, and hybridization. Many mountains are separated by 7 lowland that likely was unsuitable for high-alpine plants even during cold climatic periods. 8 We explore the relative importance of these processes using two endemic sister species: the 9 widespread Ethiopian/eastern East African Carex monostachya and the mainly western East 10 African C. -

A Rodent Described from the Mathews Range, Central Kenya
PROCEEDINGS OF THE BIOLOGICAL SOCIETY OF WASHINGTON 119(4):477-515. 2006. The status of Ototnys or estes dollmani Heller, 1912 (Muridae: Otomyinae), a rodent described from the Mathews Range, central Kenya Michael D. Carleton* and Ellen Schaefer Byrne (MDC) Department of Vertebrate Zoology, National Museum of Natural History, Smithsonian Institution, Washington, D.C. 20560-0108, U.S.A., e-mail: [email protected]; (ESB) 4209 Lawn Avenue, Western Springs, Illinois 60558, U.S.A. Abstract.•Morphological and morphometric comparisons of Otomys orestes dollmani, known only from Mount Gargues in the Mathews Range, central Kenya, indicate that the taxon is a valid species distinct from other African forms under which it has been previously synonymized (O. irroratus, O. orestes, O. tropicalis). Based also on these comparisons, the morphological recognition and distribution of O. orestes (including thomasi Osgood) are further clarified in relation to O. tropicalis (including elgonis Wroughton) in Kenyan mountains and O. typus proper in Ethiopian highlands; another taxon relegated to junior synonymy within O. typus, O. uzungwensis Lawrence and Loveridge from south-central Tanzania, is resurrected to species. Certain traditional characters used in Otomys taxonomy, in particular molar lamination, demonstrate conservative patterns of variation that complement spatial structure derived from morphometric analyses of craniometric data and that vindicate their continued utility in delimiting species. We argue that uncritical emphasis of polytypic species, applied following the biological species concept during the latter 1900s, has led to chronic underestimation of species diversity of Otomys confined to the Afromontane Biotic Region in eastern Africa, in particular those populations that inhabit afroalpine environments.