The Impact of Delays on Airline Frequencies Under Different Route Structures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![Contents [Edit] Africa](https://docslib.b-cdn.net/cover/9562/contents-edit-africa-79562.webp)
Contents [Edit] Africa
Low cost carriers The following is a list of low cost carriers organized by home country. A low-cost carrier or low-cost airline (also known as a no-frills, discount or budget carrier or airline) is an airline that offers generally low fares in exchange for eliminating many traditional passenger services. See the low cost carrier article for more information. Regional airlines, which may compete with low-cost airlines on some routes are listed at the article 'List of regional airlines.' Contents [hide] y 1 Africa y 2 Americas y 3 Asia y 4 Europe y 5 Middle East y 6 Oceania y 7 Defunct low-cost carriers y 8 See also y 9 References [edit] Africa Egypt South Africa y Air Arabia Egypt y Kulula.com y 1Time Kenya y Mango y Velvet Sky y Fly540 Tunisia Nigeria y Karthago Airlines y Aero Contractors Morocco y Jet4you y Air Arabia Maroc [edit] Americas Mexico y Aviacsa y Interjet y VivaAerobus y Volaris Barbados Peru y REDjet (planned) y Peruvian Airlines Brazil United States y Azul Brazilian Airlines y AirTran Airways Domestic y Gol Airlines Routes, Caribbean Routes and y WebJet Linhas Aéreas Mexico Routes (in process of being acquired by Southwest) Canada y Allegiant Air Domestic Routes and International Charter y CanJet (chartered flights y Frontier Airlines Domestic, only) Mexico, and Central America y WestJet Domestic, United Routes [1] States and Caribbean y JetBlue Airways Domestic, Routes Caribbean, and South America Routes Colombia y Southwest Airlines Domestic Routes y Aires y Spirit Airlines Domestic, y EasyFly Caribbean, Central and -
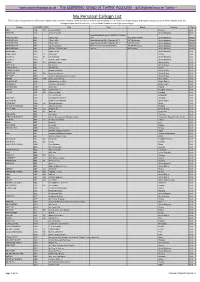
My Personal Callsign List This List Was Not Designed for Publication However Due to Several Requests I Have Decided to Make It Downloadable
- www.egxwinfogroup.co.uk - The EGXWinfo Group of Twitter Accounts - @EGXWinfoGroup on Twitter - My Personal Callsign List This list was not designed for publication however due to several requests I have decided to make it downloadable. It is a mixture of listed callsigns and logged callsigns so some have numbers after the callsign as they were heard. Use CTL+F in Adobe Reader to search for your callsign Callsign ICAO/PRI IATA Unit Type Based Country Type ABG AAB W9 Abelag Aviation Belgium Civil ARMYAIR AAC Army Air Corps United Kingdom Civil AgustaWestland Lynx AH.9A/AW159 Wildcat ARMYAIR 200# AAC 2Regt | AAC AH.1 AAC Middle Wallop United Kingdom Military ARMYAIR 300# AAC 3Regt | AAC AgustaWestland AH-64 Apache AH.1 RAF Wattisham United Kingdom Military ARMYAIR 400# AAC 4Regt | AAC AgustaWestland AH-64 Apache AH.1 RAF Wattisham United Kingdom Military ARMYAIR 500# AAC 5Regt AAC/RAF Britten-Norman Islander/Defender JHCFS Aldergrove United Kingdom Military ARMYAIR 600# AAC 657Sqn | JSFAW | AAC Various RAF Odiham United Kingdom Military Ambassador AAD Mann Air Ltd United Kingdom Civil AIGLE AZUR AAF ZI Aigle Azur France Civil ATLANTIC AAG KI Air Atlantique United Kingdom Civil ATLANTIC AAG Atlantic Flight Training United Kingdom Civil ALOHA AAH KH Aloha Air Cargo United States Civil BOREALIS AAI Air Aurora United States Civil ALFA SUDAN AAJ Alfa Airlines Sudan Civil ALASKA ISLAND AAK Alaska Island Air United States Civil AMERICAN AAL AA American Airlines United States Civil AM CORP AAM Aviation Management Corporation United States Civil -

Media Advisory
MEDIA ADVISORY Contact: Victoria B. Moreland Director/Public Relations (239) 590-4504 [email protected] FOR IMMEDIATE RELEASE MN 08-18 USA3000 TO RESUME MILWAUKEE-FORT MYERS SERVICE The Lee County Port Authority is pleased to announce that USA3000 Airlines (U5) will resume service between Milwaukee’s General Mitchell International Airport (MKE) and Southwest Florida International Airport (RSW) on Dec. 18, 2008. USA3000 will operate nonstop service between RSW-MKE six days a week (everyday except Saturdays). USA3000 currently offers nonstop service to/from RSW to Chicago-O’Hare (ORD), Cincinnati (CVG), Cleveland (CLE), Detroit-Metro (DTW), Pittsburgh (PIT), Philadelphia (PHL) and St. Louis (STL). For more information, please see the below news release from USA3000 or visit www.usa3000.com. NOV. 18, 2008 NEWS RELEASE Airline Media Contact: Chesley Turner (610) 325-1857 [email protected] USA3000 Airlines Resumes Service to Milwaukee Philadelphia – November 11th 2008 – USA3000 Airlines has announced that the company will be resuming service from Milwaukee’s General Mitchell International Airport to Ft. Myers’ Southwest Florida International Airport. Service resumes on December 18th, 2008 and direct flights will operate six days a week. USA3000 has not flown from Milwaukee since late 2005. Loyal customers as well as recent decreases in oil prices and reductions in airline capacities are listed as integral factors in the company’s decision to resume service. USA3000 Airlines will also resume select flights from Milwaukee to Cancun (Mexico), Punta Cana (Dominican Republic), Puerto Vallarta (Mexico), and Montego Bay (Jamaica). To celebrate its resumed service, the air carrier is offering low introductory fares to Ft. -

Flight and Duty Time Limitations and Rest Requirements Aviation Rulemaking Committee
U.S. DEPARTMENT OF TRANSPORTATION FEDERAL AVIATION ADMINISTRATION Effective Date: June 24, 2009 SUBJ: Flight and Duty Time Limitations and Rest Requirements Aviation Rulemaking Committee 1. PURPOSE. This document establishes the Flight and Duty Time Limitations and Rest Requirements Aviation Rulemaking Committee (ARC) according to the Administrator's authority under Title 49 of the United States Code (49 U.S.C.), section 106(p)(5). 2. DISTRIBUTION. This document is distributed to the director level in the Offices of Rulemaking; International Aviation; Chief Counsel; Flight Standards; Aerospace Medicine; Budget. BACKGROUND. a. On June 10, 2009, FAA Administrator J. Randolph Babbitt testified before the Senate on the "FAA's Role in the Oversight of Air Carriers." He addressed issues regarding pilot training and qualifications, fljght crew fatigue, and consistency of safety standards and compliance between air transportation operators, and committed to " ...assessing the safety of our system and taking the appropriate steps to improve [it].." b. The FAA recognizes that the effects of fatigue are universal, and the profiles of operations occurring under parts 121 and 135 are similar enough that the same fatigue mitigations should be applied across operations for flightcrew members. To carry out the Administrator's goal, the FAA is chartering an ARC that will develop recommendations regarding rulemaking on flight time limitations, duty period limits and rest requirements for pilots in operations under parts 121 and 135. 3. OBJECTIVES AND SCOPE OF THE COMMITTEE. The Flight and Duty Time Limitations and Rest Requirements ARC will provide a forum for the U.S. aviation community to discuss current approaches to mitigate fatigue found in international standards (e.g. -

Die Folgende Liste Zeigt Alle Fluggesellschaften, Die Über Den Flugvergleich Von Verivox Buchbar Sein Können
Die folgende Liste zeigt alle Fluggesellschaften, die über den Flugvergleich von Verivox buchbar sein können. Aufgrund von laufenden Updates einzelner Tarife, technischen Problemen oder eingeschränkten Verfügbarkeiten kann es vorkommen, dass einzelne Airlines oder Tarife nicht berechnet oder angezeigt werden können. 1 Adria Airways 2 Aegean Airlines 3 Aer Arann 4 Aer Lingus 5 Aeroflot 6 Aerolan 7 Aerolíneas Argentinas 8 Aeroméxico 9 Air Algérie 10 Air Astana 11 Air Austral 12 Air Baltic 13 Air Berlin 14 Air Botswana 15 Air Canada 16 Air Caraibes 17 Air China 18 Air Corsica 19 Air Dolomiti 20 Air Europa 21 Air France 22 Air Guinee Express 23 Air India 24 Air Jamaica 25 Air Madagascar 26 Air Malta 27 Air Mauritius 28 Air Moldova 29 Air Namibia 30 Air New Zealand 31 Air One 32 Air Serbia 33 Air Transat 34 Air Asia 35 Alaska Airlines 36 Alitalia 37 All Nippon Airways 38 American Airlines 39 Arkefly 40 Arkia Israel Airlines 41 Asiana Airlines 42 Atlasglobal 43 Austrian Airlines 44 Avianca 45 B&H Airlines 46 Bahamasair 47 Bangkok Airways 48 Belair Airlines 49 Belavia Belarusian Airlines 50 Binter Canarias 51 Blue1 52 British Airways 53 British Midland International 54 Brussels Airlines 55 Bulgaria Air 56 Caribbean Airlines 57 Carpatair 58 Cathay Pacific 59 China Airlines 60 China Eastern 61 China Southern Airlines 62 Cimber Sterling 63 Condor 64 Continental Airlines 65 Corsair International 66 Croatia Airlines 67 Cubana de Aviacion 68 Cyprus Airways 69 Czech Airlines 70 Darwin Airline 71 Delta Airlines 72 Dragonair 73 EasyJet 74 EgyptAir 75 -

December 2009 Passenger Airline Employment Down 3.3 Percent from December 2008
U.S Department of Transportation Office of Public Affairs 1200 New Jersey Ave., S.E. Washington, DC 20590 www.dot.gov/affairs/briefing.htm BTS Data BTS 09-10 Monday, February 22, 2010 Contact: Dave Smallen Tel: 202-366-5568 December 2009 Passenger Airline Employment Down 3.3 Percent from December 2008 U.S. scheduled passenger airlines employed 3.3 percent fewer workers in December 2009 than in December 2008, the 18th consecutive decrease in full-time equivalent employee (FTE) levels for the scheduled passenger carriers from the same month of the previous year, the U.S. Department of Transportation’s Bureau of Transportation Statistics (BTS) reported today (Tables 1, 2). FTE calculations count two part-time employees as one full-time employee. BTS, a part of the Research and Innovative Technology Administration, reported that the December FTE total of 379,100 for the scheduled passenger carriers was 12,900 below December 2008 and the lowest total for any month since 1993 (Table 3). Historic employment data can be found on the BTS web site. Six of the seven network airlines decreased employment from December 2008 to December 2009. Delta Air Lines, which is completing its merger with Northwest Airlines, was the lone network carrier to increase employment (Table 9). Network airlines operate a significant portion of their flights using at least one hub where connections are made for flights to down-line destinations or spoke cities. Low-cost carriers Southwest Airlines, Spirit Airlines and Frontier Airlines also reported decreases from December 2008 (Table 12). Regional carriers American Eagle Airlines, SkyWest Airlines, Comair, Atlantic Southeast Airlines, Pinnacle Airlines, Horizon Air, Mesa Airlines, Air Wisconsin Airlines, Mesaba Airlines, PSA Airlines and Colgan Airlines also reported reduced employment levels compared to last year (Table 15). -

Leading Travel Companies Report Success with Travelzoo's Newsflash
Travelzoo Inc. 590 Madison Avenue, 21st Floor New York, NY 10022 Phone (212) 521-4200 Fax (212) 521-4230 Contact: Christie Ly (212) 521-4218 [email protected] FOR IMMEDIATE RELEASE Leading Travel Companies Report Success with Travelzoo’s Newsflash™ Innovative Media Service Gives Travel Providers a Quick Way To Inform Millions of Consumers About Time-sensitive Travel Specials NEW YORK, June 29, 2004 – Travelzoo (NASDAQ: TZOO), the Internet’s largest publisher of sales and specials available directly from hundreds of travel companies, today announced that its recently launched Newsflash™ e-mail alert service has proven to be a resounding success with participating travel providers. Newsflash is the first Internet alert service that informs millions of consumers about time-sensitive travel offers that are test-booked and independently reviewed in less than two hours. Through Newsflash, travel companies can quickly announce newsworthy deals to as many as 3.7 million registered travel shoppers in 18 geographic markets. Travelzoo's producers evaluate and test book each offer to ensure its relevance for a particular market. Once approved for publication, the offer is e-mailed only to subscribers in the corresponding geographic area. Travel companies citing success with Travelzoo's Newsflash alert service include: USA3000 Airlines "As a growing airline, we were looking for a cost-effective and targeted media vehicle to quickly grow awareness and bookings of our routes. Travelzoo's Newsflash offered a solid value proposition in online marketing. Our Detroit promotion resulted in significant bookings, which we can attribute directly to Newsflash. Since then, we have run six additional Newsflash promotions and are very happy with the results,” said Angus Kinnear, COO. -

Growing Number of Low-Fare Airlines Offering Frequent Flyer Programs
Airline Industry Analysis - Press Release Contact: Jay Sorensen For inquiries: 414-961-1939 Growing Number of Low-Fare Airlines Offering Frequent Flyer Programs Comparison of twelve U.S based low-cost carriers indicates the largest five provide frequent flyer programs to their passengers. March 15, 2004, Shorewood, WI. The IdeaWorks Company has compared the leading low-fare airlines in the United States on the basis of frequent flyer program benefits. Twelve airlines were included in the survey: AirTran Airways, Allegiant Air, ATA Airlines, Frontier Airlines, jetBlue Airways, Pan Am, Southeast Airlines, Southwest Airlines, Spirit Airlines, Sun Country Airlines, TransMeridian Airlines and USA3000 Airlines. These airlines are among those recognized by the USDOT as low-fare carriers due to operating cost advantages enjoyed over network carriers such as American Airlines and Northwest Airlines. Recently launched low-fare brands operated by network carriers, such as Song by Delta Air Lines and Ted by United Airlines, were not included in the survey completed by IdeaWorks. Five low-cost carriers, representing the largest airlines of the group in terms of available passenger seats, were found to offer traditional frequent flyer programs: AirTran Airways, ATA Airlines, Frontier Airlines, jetBlue and Southwest Airlines. These programs allow passengers to accrue benefits from flight activity in the form of miles, points or credits; which may be redeemed for free airline travel. Southwest has the longest tenure among the group with the launch of a frequent flyer program in 1987. The number of low-fare carriers offering frequent flyer programs grew to five airlines by 2002. All of these programs offered the feature of automated flight tracking by November, 2003. -

Pilot Fatigue
S. HRG. 111–515 AVIATION SAFETY: PILOT FATIGUE HEARING BEFORE THE SUBCOMMITTEE ON AVIATION OPERATIONS, SAFETY, AND SECURITY OF THE COMMITTEE ON COMMERCE, SCIENCE, AND TRANSPORTATION UNITED STATES SENATE ONE HUNDRED ELEVENTH CONGRESS FIRST SESSION DECEMBER 1, 2009 Printed for the use of the Committee on Commerce, Science, and Transportation ( U.S. GOVERNMENT PRINTING OFFICE 54–497 PDF WASHINGTON : 2010 For sale by the Superintendent of Documents, U.S. Government Printing Office Internet: bookstore.gpo.gov Phone: toll free (866) 512–1800; DC area (202) 512–1800 Fax: (202) 512–2104 Mail: Stop IDCC, Washington, DC 20402–0001 VerDate Nov 24 2008 07:59 Jul 08, 2010 Jkt 054497 PO 00000 Frm 00001 Fmt 5011 Sfmt 5011 S:\WPSHR\GPO\DOCS\54497.TXT SCOM1 PsN: JACKIE SENATE COMMITTEE ON COMMERCE, SCIENCE, AND TRANSPORTATION ONE HUNDRED ELEVENTH CONGRESS FIRST SESSION JOHN D. ROCKEFELLER IV, West Virginia, Chairman DANIEL K. INOUYE, Hawaii KAY BAILEY HUTCHISON, Texas, Ranking JOHN F. KERRY, Massachusetts OLYMPIA J. SNOWE, Maine BYRON L. DORGAN, North Dakota JOHN ENSIGN, Nevada BARBARA BOXER, California JIM DEMINT, South Carolina BILL NELSON, Florida JOHN THUNE, South Dakota MARIA CANTWELL, Washington ROGER F. WICKER, Mississippi FRANK R. LAUTENBERG, New Jersey GEORGE S. LEMIEUX, Florida MARK PRYOR, Arkansas JOHNNY ISAKSON, Georgia CLAIRE MCCASKILL, Missouri DAVID VITTER, Louisiana AMY KLOBUCHAR, Minnesota SAM BROWNBACK, Kansas TOM UDALL, New Mexico MIKE JOHANNS, Nebraska MARK WARNER, Virginia MARK BEGICH, Alaska ELLEN L. DONESKI, Staff Director JAMES REID, Deputy Staff Director BRUCE H. ANDREWS, General Counsel ANN BEGEMAN, Acting Republican Staff Director BRIAN M. HENDRICKS, Republican Chief Counsel SUBCOMMITTEE ON AVIATION OPERATIONS, SAFETY, AND SECURITY BYRON L. -

Existing Facilities
Existing Facilities St. Petersburg-Clearwater International Airport is served by a number of airside and landside facilities. Four runways serve the airport. These runways are Runway 04/22 (5,903 feet long by 150 feet wide), Runway 09/27 (5,165 feet long by 150 feet wide), Runway 17L/35R (9,730 feet long by 150 feet wide), and Runway 17R/35L (4,000 feet long by 75 feet wide). These runways are all asphalt and are generally in good to excellent condition. The runways are served by parallel taxiways, except Runway 17R/35L. The airport has a 143,980-square foot passenger terminal building, served by 11 aircraft gates. The airport also has two Fixed Base Operators to serve general aviation pilots and passengers. Currently, there are 76 tie-downs for general aviation aircraft, and between the airport’s T-Hangars and conventional hangars, 233 covered parking spaces for aircraft. The most recent update to the St. Petersburg-Clearwater International Airport’s Master Plan was completed in January 2004. The following projects are either currently underway or planned for the near future: 1. Terminal Building Renovations 2. Security Enhancements 3. Runway 4/22 Resurfacing 4. Parking Lot Improvements 5. Storm Water Drainage In an effort to support continued growth, the airport has identified the following long term improvement projects: 1. Terminal Building Renovation – Phase II 2. Runway 9/27 Conversion to a Taxiway 3. Airport Golf Course Redevelopment – Aviation & Business Park Use 4. Rehabilitation of Runway 17L/35R Current and Forecast Demand COMMERCIAL AND GENERAL AVIATION St. Petersburg-Clearwater International Airport serves the needs of commercial airlines, military, air cargo, as well as all facets of general aviation. -

2030 Twin Cities Aviation System Technical Report
Twin Cities Aviation System Technical Report December 2009 Prepared for: Metropolitan Council Prepared by: With: KRAMER aerotek and Biko Associates “The preparation of this document was financed in part through a planning grant from the Federal Aviation Administration (FAA) as approved under the Airport and Airway Improvement Act of 1982. The contents of this report reflect the views of the Consultant, which is responsible for the fact and the accuracy of the data depicted herein, and do not necessarily reflect the official views or policy of the FAA. Acceptance of the report by the FAA does not in any way constitute a commitment on the part of the United States to participate in any development depicted therein, nor does it indicate that the proposed development is environmentally acceptable in accordance with applicable public laws.” Table of Contents Table of Contents Executive Summary Inventory.................................................................................................................................................. ES‐1 Aviation Industry Trends..........................................................................................................................ES‐3 Forecasts .................................................................................................................................................. ES‐4 Peer System Comparisons ....................................................................................................................... ES‐5 Airport Classification............................................................................................................................... -

December 2011 Passenger Airline Employment Rose 2.7 Percent from December 2010
U.S. Department of Transportation Office of Public Affairs 1200 New Jersey Avenue, SE Washington, DC 20590 www.dot.gov/briefing-room.html BTS Data BTS 10-12 Wednesday, February 29, 2012 Contact: Dave Smallen Tel: 202-366-5568 December 2011 Passenger Airline Employment Rose 2.7 Percent from December 2010 Scheduled Passenger Airline Full-Time Equivalent Employees, January 2010-December 2011 U.S. scheduled passenger airlines employed 2.7 percent more workers in December 2011 than they did in December 2010, the U.S. Department of Transportation’s Bureau of Transportation Statistics (BTS) reported today. This is the 13th consecutive month that full-time equivalent employee (FTE) levels for the scheduled passenger carriers have been higher than the same month of the previous year (Tables 1, 2). FTE calculations count two part-time employees as one full-time employee. BTS, a part of the Research and Innovative Technology Administration, reported that the December FTE total of 389,728 for the scheduled passenger carriers was 10,077 more than that of December 2010 (Table 3). These monthly increases reflect gradual improvement in the industry’s employment following declines that began in July 2008 (Table 2). Historic employment data can be found on the BTS web site. - more - AIRLINE EMPLOYMENT PRESS RELEASE ADD ONE Of the network airlines, only Delta Air Lines, which has been eliminating duplicate positions following its merger with Northwest Airlines, decreased employment from December 2010 to December 2011. Continental Airlines reported 14.5 percent more FTEs in December 2011 than in December 2010, the largest increase among the network carriers.