Energy Dispersive X-Ray Microanalysis an Introduction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Electron Microprobe Analysis Course 12.141 Notes MIT Electron
Electron Microprobe Analysis Course 12.141 Notes Dr. Nilanjan Chatterjee The electron microprobe provides a complete micron-scale quantitative chemical analysis of inorganic solids. The method is nondestructive and utilizes characteristic x-rays excited by an electron beam incident on a flat surface of the sample. This course provides an introduction to the theory of x-ray microanalysis by wavelength and energy dispersive spectrometry (WDS and EDS), ZAF matrix correction procedures, and scanning electron imaging techniques using backscattered electron (BE), secondary electron (SE), x-ray (elemental mapping), and cathodoluminescence (CL) signals. Lab sessions involve hands- on use of the JEOL JXA-8200 Superprobe. MIT Electron Microprobe Facility Massachusetts Institute of Technology Department of Earth, Atmospheric & Planetary Sciences Room: 54-1221, Cambridge, MA 02139 Phone: (617) 253-1995; Fax: (617) 253-7102 e-mail: [email protected] web: http://web.mit.edu/e-probe/www/ Nilanjan ChatterjeeMIT, Cambridge, MA, USA October 2017 2 TABLE OF CONTENTS Page number 1. INTRODUCTION 3 2. ELECTRON SPECIMEN INTERACTIONS 5 2.1. ELASTIC SCATTERING 5 2.1.1. Electron backscattering 5 2.1.2. Electron interaction volume 6 2.2. INELASTIC SCATTERING 7 2.2.1. Secondary electron generation 7 2.2.2. Characteristic x-ray generation: inner-shell ionization 7 2.2.3. X-ray production volume 10 2.2.4. Bremsstrahlung or continuum x-ray generation 11 2.2.5. Cathodoluminescence 12 3. QUANTITATIVE X-RAY SPECTROMETRY 13 3.1. MATRIX CORRECTIONS 14 3.1.1. Atomic number correction (Z) 14 3.1.2. Absorption correction (A) 16 3.1.3. -

Electron Probe Microanalysis (EPMA) in the Earth Sciences
This is a repository copy of Electron probe microanalysis (EPMA) in the Earth Sciences. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/135874/ Version: Accepted Version Proceedings Paper: Walshaw, R orcid.org/0000-0002-8319-9312 (Accepted: 2018) Electron probe microanalysis (EPMA) in the Earth Sciences. In: Book of Tutorials and Abstracts. Microbeam Analysis in the Earth Sciences, 13th EMAS Regional Workshop, 04-07 Sep 2018, University of Bristol. (In Press) Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ ELECTRON PROBE MICROANALYSIS (EPMA) IN THE EARTH SCIENCES R.D. Walshaw University of Leeds, School of Earth & Environment, Leeds Electron Microscopy & Spectroscopy Centre Woodhouse Lane, Leeds LS2 9JT, Great Britain e-mail: [email protected] 75 1. INTRODUCTION Electron probe microanalysis (EPMA) is a non-destructive, standards-based microanalytical technique, yielding fully quantitative chemical analyses of solid materials at the micron scale. -

Quick Reference Guide Scientific Instruments and Software
Scientific Instruments and Software Quick Reference Guide Elemental Analysis Gas Chromatography Inorganic Mass Spectrometry Life Sciences Mass Spectrometry LIMS and Laboratory Software Liquid Chromatography Molecular Spectroscopy and Microanalysis Scientific Instrumentation Services Surface Analysis Scientific Instruments and Software Quick Reference Guide Thermo Scientific products help to solve your most demanding analytical challenges with our world-class portfolio of products and technologies. Whether for your laboratory, field or industrial settings we offer a complete spectrum of solutions including automation, accessories, consumables, software & reference databases, service and support. Elemental Analysis Gas Chromatography Inorganic Mass Spectrometry Life Sciences Mass Spectrometry LIMS and Laboratory Software Liquid Chromatography Molecular Spectroscopy and Microanalysis Scientific Instrumentation Services Surface Analysis ELEMENTAL ANALYSIS www.thermoscientific.com/elemental Cement • Clinical Toxicology • Environmental Food, Beverage and Agriculture • Metals and Materials Petrochemical • Semiconductor Organic and inorganic analysis in environmental, health and industrial applications require instruments that can handle a variety of sample types, volumes and demanding detection limits. Results need to be reliable, fast and easy to obtain. Our range elemental analysis solutions enable laboratories to analyze more samples with greater accuracy, simplicity and cost-effectiveness. iCE 3000 Series FLASH 2000 iCAP 6000 Series XSERIES 2 ELEMENT -

Microchemistry-The Present and the Future
MICROCHEMISTRY-THE PRESENT AND THE FUTURE P. J. ELVING Department of Chemistry, University of Michigan, Ann Arbor, Michigan, U.S.A. INTRODUCTION The goals sought in the practice of analytical chemistry can be conven iently summarized as the three S's of selectivity, sensitivity and speed. Selectivity or specijicity means the ability to detect and determine one sub stance in the presence of other substances with special reference to those other substances which are commonly associated with the desired constit uent and which might be expected to interfere with its identification and determina tion. Sensitivity means one or both of the senses in which this word is customarily used: absolute sensitiviry, i.e., the smallest amount of material which will give a satisfactory signal with the particular approach being used, and concen trational sensitivity, i.e., the lowest concentration of material which will give a sa tisfactory signal. There is obviously no need to define speed, since the latter is an ever-present and necessary goal in the hurly-burly of contemporary life. The only comment that needs tobe madeisthat the need for speed may vary in differ ent situations. In the dissolution of a mineral preliminary to analysis, the time required for the initial evaporation with acid is usually not a critical factor. On the other hand, in the determination of some elements by acti vation analysis, the time allowable between removal from the activating reactor and the counting of the induced activity may be only a few precious minutes. Since the latter part of the nineteenth century when microchemistry was first recognized by chemists as a specific subject, microchemistry has con tributed greatly to the attainment of the goals of selectivity, sensitivity and speed. -

UV-Vis Spectroscopy
DE GRUYTER Physical Sciences Reviews. 2018; 20180008 Marcello Picollo1 / Maurizio Aceto2 / Tatiana Vitorino1,3 UV-Vis spectroscopy 1 Istituto di Fisica Applicata “Nello Carrara” del Consiglio Nazionale delle Ricerche, Via Madonna del piano 10, 50019 Sesto Fiorentino, Firenze, Italy, E-mail: [email protected], [email protected] 2 Dipartimento di Scienze e Innovazione Tecnologica (DISIT), Università degli Studi del Piemonte Orientale, viale Teresa Michel, 11, 15121 Alessandria, Italy, E-mail: [email protected] 3 Department of Conservation and Restoration and LAQV-REQUIMTE, Faculty of Sciences and Technology, NOVA University of Lisbon, 2829-516 Caparica, Portugal, E-mail: [email protected] Abstract: UV-Vis reflectance spectroscopy has been widely used as a non-invasive method for the study of cultural her- itage materials for several decades. In particular, FORS, introduced in the 1980s, allows to acquire hundreds of reflectance spectra in situ in a short time, contributing to the identification of artist’s materials. More recently, microspectrofluorimetry has also been proposed as a powerful non-invasive method for the identification of dyes and lake pigments that provides high sensitivity and selectivity. In this chapter, the concepts behind these spectroscopic methodologies will be discussed, as well as the instrumentation and measurement modes used. Case studies related with different cultural heritage materials (paintings and manuscripts, textiles, carpets and tapestries, glass, metals, and minerals), -

Reference Materials for Microanalytical Nuclear Techniques
IAEA-TECDOC-1295 Reference materials for microanalytical nuclear techniques Final report of a co-ordinated research project 1994–1999 June 2002 The originators of this publication in the IAEA were: Industrial Applications and Chemistry Section and IAEA Laboratories, Seibersdorf International Atomic Energy Agency Wagramer Strasse 5 P.O. Box 100 A-1400 Vienna, Austria REFERENCE MATERIALS FOR MICROANALYTICAL NUCLEAR TECHNIQUES IAEA, VIENNA, 2002 IAEA-TECDOC-1295 ISSN 1011–4289 © IAEA, 2002 Printed by the IAEA in Austria June 2002 FOREWORD In 1994 the IAEA established a Co-ordinated Research Project (CRP) on Reference Materials for Microanalytical Nuclear Techniques as part of its efforts to promote and strengthen the use of nuclear analytical technologies in Member States with the specific aim of improving the quality of analysis in nuclear, environmental and biological materials. The objectives of this initiative were to: identify suitable biological reference materials which could serve the needs for quality control in micro-analytical techniques, evaluate existing CRMs for use in micro-analytical investigations, evaluate appropriate sample pre-treatment procedures for materials being used for analysis with micro-analytical techniques, identify analytical techniques which can be used for characterisation of homogeneity determination, and apply such techniques to the characterization of candidate reference materials for use with micro-analytical techniques. The CRP lasted for four years and seven laboratories and the IAEA’s Laboratories in Seibersdorf participated. A number of materials including the candidate reference materials IAEA 338 (lichen) and IAEA 413 (single cell algae, elevated level) were evaluated for the distribution of elements such as Cl, K, Ca, Cr, Mn, Fe, Zn, As, Br, Rb, Cd, Hg and Pb. -

The Chemical Activators of Cathodoluminescence in Jadeite
The Chemical Activators of Cathodoluminescence in Jadeite Erin C. Dopfel A thesis presented to the faculty of Mount Holyoke College in partial fulfillment of the requirements for the degree of Bachelor of Arts with Honor Department of Earth and Environment Mount Holyoke College South Hadley, Massachusetts May 2006 Thesis Advisor: Dr. M. Darby Dyar Department Chair: Dr. Mark McMenamin ACKNOWLEDGMENTS I would like to thank my advisor, Darby Dyar, for her patience and guidance, and all the support she has shown toward this project over the past year. I am also grateful to Dean Connie Allen and Mark McMenamin, members of my thesis committee, for reading this document and providing me with extraordinarily helpful suggestions. And to the faculty of Mount Holyoke’s Department of Earth and Environment, especially Michelle Markley, Al Werner, and Steve Dunn, who have acted not only as mentors, but as true friends. Endless thanks to the donors of the Mount Holyoke Summer Research Fellowship, the Martha Godchaux Field Scholarship, and the Department of Earth and Environment funds, as well as Darby Dyar and the Sorena Sorensen, for supporting my travels and research expenses. Thanks to Mike Jercinovic at the University of Massachusetts – Amherst Microprobe Lab, who somehow managed to run all of my EPMA analyses on the shortest-notice-known-to-man. I am especially grateful to William F. McDonough and Richard Ash at the University of Maryland’s Isotope Geochemistry Lab, for allowing me to utilize their facilities to collect my LA ICP-MS data. Also, thanks to Gerard Marchand, Yarrow Rothstein, and Eli Sklute of Mount Holyoke College for helping to prepare and change ii samples, and fit messy Mössbauer curves. -

Power and Limitations of Electrophoretic Separations in Proteomics Strategies
Power and limitations of electrophoretic separations in proteomics strategies Thierry. Rabilloud 1,2, Ali R.Vaezzadeh 3 , Noelle Potier 4, Cécile Lelong1,5, Emmanuelle Leize-Wagner 4, Mireille Chevallet 1,2 1: CEA, IRTSV, LBBSI, 38054 GRENOBLE, France. 2: CNRS, UMR 5092, Biochimie et Biophysique des Systèmes Intégrés, Grenoble France 3: Biomedical Proteomics Research Group, Central Clinical Chemistry Laboratory, Geneva University Hospitals, Geneva, Switzerland 4: CNRS, UMR 7177. Institut de Chime de Strasbourg, Strasbourg, France 5: Université Joseph Fourier, Grenoble France Correspondence : Thierry Rabilloud, iRTSV/LBBSI, UMR CNRS 5092, CEA-Grenoble, 17 rue des martyrs, F-38054 GRENOBLE CEDEX 9 Tel (33)-4-38-78-32-12 Fax (33)-4-38-78-44-99 e-mail: Thierry.Rabilloud@ cea.fr Abstract: Proteomics can be defined as the large-scale analysis of proteins. Due to the complexity of biological systems, it is required to concatenate various separation techniques prior to mass spectrometry. These techniques, dealing with proteins or peptides, can rely on chromatography or electrophoresis. In this review, the electrophoretic techniques are under scrutiny. Their principles are recalled, and their applications for peptide and protein separations are presented and critically discussed. In addition, the features that are specific to gel electrophoresis and that interplay with mass spectrometry( i.e., protein detection after electrophoresis, and the process leading from a gel piece to a solution of peptides) are also discussed. Keywords: electrophoresis, two-dimensional electrophoresis, isoelectric focusing, immobilized pH gradients, peptides, proteins, proteomics. Table of contents I. Introduction II. The principles at play III. How to use electrophoresis in a proteomics strategy III.A. -
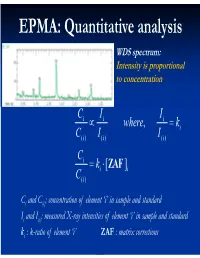
Electron Microprobe Analysis Slide 4
EPMA: Quantitative analysis WDS spectrum: Intensity is proportional to concentration C i I i Ii where, ki C( i )I i ( ) I() i C i ki [ ZAF i ] C( i ) Ci and C(i): concentration of element ‘i’ in sample and standard Ii and I(i): measured X-ray intensities of element ‘i’ in sample and standard ki : k-ratio of element ‘i’ ZAF : matrix corrections Matrix (ZAF) corrections Z : atomic number correction A : absorption correction F : fluorescence correction Atomic number (Z) correction R = CjRj Ri [ R = #X-ray photons S i generated / #photons if Z i * there were no back-scatter] Ri * S = C S S i j j [ S = -(1/)(dE/ds), * sample stopping power] Z, a function of E0 and composition Duncumb-Reed-Yakowitz method: Ri = j CjRij Rij = R' 1 - R'2 ln(R'3 Zj+25) -3 3 2 R'1 = 8.73x10 U - 0.1669 U + 0.9662 U + 0.4523 -3 3 -2 2 R'2 = 2.703x10 U - 5.182x10 U + 0.302 U - 0.1836 3 2 3 R'3 = (0.887 U - 3.44 U + 9.33 U - 6.43)/U Si = j CjSij Sij = (const) [(2Zj/Aj )/(E0+Ec)]ln[583(E0+Ec)/Jj ] where, J (keV) = (9.76Z + 58.82Z-0.19)x10-3 Z, a function of E0 and composition Al-Cu alloy 1.2 1.2 Pure metal standards Pure metal standards 1.15 1.15 1.1 1.1 1.05 1.05 1 1 AlK C CuK C 0.95 Cu 0.95 Cu Z 0.1 0.1 Z 0.9 0.3 0.9 0.3 0.5 0.5 0.85 0.7 0.85 0.7 0.9 0.9 0.8 0.8 10 15 20 10 15 20 E0 (keV) E0 (keV) 1.2 1.2 CuAl standard CuAl standard 1.15 2 1.15 2 1.1 1.1 1.05 1.05 1 1 AlK C CuK C 0.95 Cu 0.95 Cu Z 0.1 0.1 Z 0.9 0.3 0.9 0.3 0.5 0.5 0.85 0.7 0.85 0.7 0.9 0.9 0.8 0.8 10 15 20 10 15 20 E0 (keV) E0 (keV) X-ray absorption -(/)(x) -(/)( z cosec) I = I0 exp = I0 -

ANL-7917 Chemical Separations Processes for Plutonium and Uranium
ANL-7917 Chemical Separations Processes for Plutonium and Uranium ARGONNE NATIONAL LABORATORY 9700 South Cass Avenue Argonne, Illinois 60439 DEVELOPMENT STUDIES ON A FLUIDIZED-BED PROCESS FOR CONVERSION OF U/Pu NITRATES TO OXIDES Part 1. Laboratory-scale Denitration Studies by S. Vogler, D. E. Grosvenor, N. M. Levitz, and F. G. Teats Chemical Engineering Division April 1972 NOTICE- This report was prepared as an account of work sponsored by the United States Government. Neither the United States nor the United States Atomic Energy Commission, nor any of their employees, nor any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, com• pleteness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. BOTBimON DF THIS DOCUMENT IS ONLI DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency Thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. -

Electron Probe Microanalysis
Electron probe microanalysis Essential Knowledge Briefings First Edition, 2015 2 ELECTRON PROBE MICROANALYSIS Front cover image: high-resolution X-ray maps of copper (Cu), zinc (Zn) and silver (Ag) illustrating the interdiffusion zone between the main material (Cu) and the brazing material (Ag-Zn). Data acquired with the SXFiveFE at 10keV, 30nA © 2015 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, UK Microscopy EKB Series Editor: Dr Julian Heath Spectroscopy and Separations EKB Series Editor: Nick Taylor ELECTRON PROBE MICROANALYSIS 3 CONTENTS 4 INTRODUCTION 6 HISTORY AND BACKGROUND 13 IN PRACTICE 22 PROBLEMS AND SOLUTIONS 28 WHAT’S NEXT? About Essential Knowledge Briefings Essential Knowledge Briefings, published by John Wiley & Sons, comprise a series of short guides to the latest techniques, appli - cations and equipment used in analytical science. Revised and updated annually, EKBs are an essential resource for scientists working in both academia and industry looking to update their understanding of key developments within each specialty. Free to download in a range of electronic formats, the EKB range is available at www.essentialknowledgebriefings.com 4 ELECTRON PROBE MICROANALYSIS INTRODUCTION Electron probe microanalysis (EPMA) is an analytical technique that has stood the test of time. Not only is EPMA able to trace its origins back to the discovery of X-rays at the end of the nineteenth century, but the first commercial instrument appeared over 50 years ago. Nevertheless, EPMA remains a widely used technique for determining the elemental composition of solid specimens, able to produce maps showing the distribution of elements over the surface of a specimen while also accurately measuring their concentrations. -

The Electron Microprobe Laboratory at Arizona State University
47th Lunar and Planetary Science Conference (2016) 3018.pdf THE ELECTRON MICROPROBE LABORATORY AT ARIZONA STATE UNIVERSITY. A. Wittmann1, D. Convey1, T. Sharp1, M. Wadhwa2, P. Buseck3, and K. Hodges4 1LeRoy Eyring Center for Solid State Science, Arizona State University, Box 871704, Tempe, AZ 85287-1704, [email protected]; 2Center for Meteorite Studies-School of Earth and Space Exploration, Arizona State University, Box 871404, Tempe, AZ 85287; 3School of Molecular Sciences, Arizona State University, Box 871604, Tempe, AZ 85287-1604; 4School of Earth and Space Exploration, Arizona State University, Box 876004, Tempe, AZ 85287-6004. Introduction: In 2011, Arizona State University For instrument control, we can utilize the custom- replaced their 25 year old electron microprobe with a ized JEOL system software and the PC-based Probe state-of-the-art JEOL JXA-8530F field emission in- for Windows software. strument. Our facility was partially funded by NASA Summary Analytical Capabilities: The electron and serves as an investigator facility instrument for microprobe laboratory at Arizona State University NASA’s Planetary Science Research Program. allows to determine the chemical composition of solid Technical Capacities: The JEOL JXA-8530F materials up to 10 cm in size that are stable under high HyperProbe is an electron microscope that has a nomi- vacuum. The non-destructive analytical technique does nal imaging resolution of 3 nm with a X-ray spectrom- not require special sample preparation and produces eter for non-destructive X-ray