Electron Microprobe Analysis Course 12.141 Notes MIT Electron
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Laser Raman Microprobing Techniques P
LASER RAMAN MICROPROBING TECHNIQUES P. Dhamelincourt, J. Barbillat, M. Delhaye To cite this version: P. Dhamelincourt, J. Barbillat, M. Delhaye. LASER RAMAN MICROPROBING TECHNIQUES. Journal de Physique Colloques, 1984, 45 (C2), pp.C2-249-C2-253. 10.1051/jphyscol:1984255. jpa- 00223968 HAL Id: jpa-00223968 https://hal.archives-ouvertes.fr/jpa-00223968 Submitted on 1 Jan 1984 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. JOURNAL DE PHYSIQUE Colloque C2, suppldment au n02, Tome 45, fdvrier 1984 page C2-249 LASER RAMAN MICROPROBING TECHNIQUES P. Dhamelincourt, J. Barbillat and M. Delhaye Laboratoire de Spectrochimie Infrarouge et Raman, C. N. R. S., lhziversitB des Sciences et Techniques de LiZZe, B&. C. 5, 59655 ViZZeneuve d 'Ascq Cedex, France @sun6 - L1int6r&t de la microspectrcm6trie Raman pour l'analyse mol6culaire non destructive ainsi que 1'6volution des techniques sont pr6sentBs. Quelques exem- ples d'application illustrent l'exps6. Abstract - The analytical potential of micr0Fm-w spectroscopy for non des- tructive mlecular analysis is presented. -

Electron Probe Microanalysis (EPMA) in the Earth Sciences
This is a repository copy of Electron probe microanalysis (EPMA) in the Earth Sciences. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/135874/ Version: Accepted Version Proceedings Paper: Walshaw, R orcid.org/0000-0002-8319-9312 (Accepted: 2018) Electron probe microanalysis (EPMA) in the Earth Sciences. In: Book of Tutorials and Abstracts. Microbeam Analysis in the Earth Sciences, 13th EMAS Regional Workshop, 04-07 Sep 2018, University of Bristol. (In Press) Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ ELECTRON PROBE MICROANALYSIS (EPMA) IN THE EARTH SCIENCES R.D. Walshaw University of Leeds, School of Earth & Environment, Leeds Electron Microscopy & Spectroscopy Centre Woodhouse Lane, Leeds LS2 9JT, Great Britain e-mail: [email protected] 75 1. INTRODUCTION Electron probe microanalysis (EPMA) is a non-destructive, standards-based microanalytical technique, yielding fully quantitative chemical analyses of solid materials at the micron scale. -

Microprobe Operating Procedure
TWS-ESS-DP-07, R3 MICROPROBE OPERATING PROCEDURE Effective Date $1fj3 O/il ga" A*4,- Roland Hagan Date Preparer / /A Dad-, David Vaniman Technical Reviewer =AQ vc) Henry Paul Nunas Date Quality Assurane Project Leader TechnicaMrojeci Officer .B912190174 891211 -N !PDR WASTE WM-11 PDC TWS-ESS-DP-07, R3 Page 1 of 11 MICROPROBE OPERATING PROCEDURE 1.0 PURPOSE The purpose of this procedure is to allow an investigator to bring the Electron Microprobe from a standby condition to an analysis condition, perform one or more analyses, and when finished, return the system to a standby condition. 2.0 SCOPE This procedure describes the start-up, calibration, quantitative analysis and shut-down routines for the Electron Microprobe. Requirements for Los Alamos Yucca Mountain Project (LA YMP) analytical work are listed throughout this procedure. 3.0 APPLICABLE DOCUMENTS Documents referenced in this procedure are: Cameca Technical Manual, Option A-21 Tracor Northern Operators Manual, 1988 SANDIA TASKS: A Subroutined Electron Microprobe Automation system, Sandia Report 2037, 1985 CONFIG8 A Configuration File Generator for SANDIA TASKS, Sandia Report TWS-ESS-DP-06, 2035,1985 Operating Instructions For the Ladd Vacuum Evaporator For Carbon Coating TWS-ESS-DP. 122, Preparation of Electron Microprobe Standard Mounts TWS-ESS-DP-101, Procedure for Identification and Control for Mineralogy-Petrology TWS-QAS-QP-02.1, Los Alamos YMP Personnel Certification Procedure TWS-ESS-DP-125, Certification of Standards for Microanalysis TWS-QAS-QP.3.1, LANL, Yucca Mo ain Project Computer Software Control 4.0 RESPONSIBILrITES 4.1 It is the responsibility of the Operator to ascertain that all Electron Microprobe systems are operational before an Investigator begins a microanalysis session. -

The Chemical Activators of Cathodoluminescence in Jadeite
The Chemical Activators of Cathodoluminescence in Jadeite Erin C. Dopfel A thesis presented to the faculty of Mount Holyoke College in partial fulfillment of the requirements for the degree of Bachelor of Arts with Honor Department of Earth and Environment Mount Holyoke College South Hadley, Massachusetts May 2006 Thesis Advisor: Dr. M. Darby Dyar Department Chair: Dr. Mark McMenamin ACKNOWLEDGMENTS I would like to thank my advisor, Darby Dyar, for her patience and guidance, and all the support she has shown toward this project over the past year. I am also grateful to Dean Connie Allen and Mark McMenamin, members of my thesis committee, for reading this document and providing me with extraordinarily helpful suggestions. And to the faculty of Mount Holyoke’s Department of Earth and Environment, especially Michelle Markley, Al Werner, and Steve Dunn, who have acted not only as mentors, but as true friends. Endless thanks to the donors of the Mount Holyoke Summer Research Fellowship, the Martha Godchaux Field Scholarship, and the Department of Earth and Environment funds, as well as Darby Dyar and the Sorena Sorensen, for supporting my travels and research expenses. Thanks to Mike Jercinovic at the University of Massachusetts – Amherst Microprobe Lab, who somehow managed to run all of my EPMA analyses on the shortest-notice-known-to-man. I am especially grateful to William F. McDonough and Richard Ash at the University of Maryland’s Isotope Geochemistry Lab, for allowing me to utilize their facilities to collect my LA ICP-MS data. Also, thanks to Gerard Marchand, Yarrow Rothstein, and Eli Sklute of Mount Holyoke College for helping to prepare and change ii samples, and fit messy Mössbauer curves. -
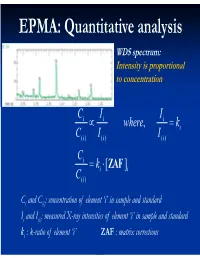
Electron Microprobe Analysis Slide 4
EPMA: Quantitative analysis WDS spectrum: Intensity is proportional to concentration C i I i Ii where, ki C( i )I i ( ) I() i C i ki [ ZAF i ] C( i ) Ci and C(i): concentration of element ‘i’ in sample and standard Ii and I(i): measured X-ray intensities of element ‘i’ in sample and standard ki : k-ratio of element ‘i’ ZAF : matrix corrections Matrix (ZAF) corrections Z : atomic number correction A : absorption correction F : fluorescence correction Atomic number (Z) correction R = CjRj Ri [ R = #X-ray photons S i generated / #photons if Z i * there were no back-scatter] Ri * S = C S S i j j [ S = -(1/)(dE/ds), * sample stopping power] Z, a function of E0 and composition Duncumb-Reed-Yakowitz method: Ri = j CjRij Rij = R' 1 - R'2 ln(R'3 Zj+25) -3 3 2 R'1 = 8.73x10 U - 0.1669 U + 0.9662 U + 0.4523 -3 3 -2 2 R'2 = 2.703x10 U - 5.182x10 U + 0.302 U - 0.1836 3 2 3 R'3 = (0.887 U - 3.44 U + 9.33 U - 6.43)/U Si = j CjSij Sij = (const) [(2Zj/Aj )/(E0+Ec)]ln[583(E0+Ec)/Jj ] where, J (keV) = (9.76Z + 58.82Z-0.19)x10-3 Z, a function of E0 and composition Al-Cu alloy 1.2 1.2 Pure metal standards Pure metal standards 1.15 1.15 1.1 1.1 1.05 1.05 1 1 AlK C CuK C 0.95 Cu 0.95 Cu Z 0.1 0.1 Z 0.9 0.3 0.9 0.3 0.5 0.5 0.85 0.7 0.85 0.7 0.9 0.9 0.8 0.8 10 15 20 10 15 20 E0 (keV) E0 (keV) 1.2 1.2 CuAl standard CuAl standard 1.15 2 1.15 2 1.1 1.1 1.05 1.05 1 1 AlK C CuK C 0.95 Cu 0.95 Cu Z 0.1 0.1 Z 0.9 0.3 0.9 0.3 0.5 0.5 0.85 0.7 0.85 0.7 0.9 0.9 0.8 0.8 10 15 20 10 15 20 E0 (keV) E0 (keV) X-ray absorption -(/)(x) -(/)( z cosec) I = I0 exp = I0 -

ANL-7917 Chemical Separations Processes for Plutonium and Uranium
ANL-7917 Chemical Separations Processes for Plutonium and Uranium ARGONNE NATIONAL LABORATORY 9700 South Cass Avenue Argonne, Illinois 60439 DEVELOPMENT STUDIES ON A FLUIDIZED-BED PROCESS FOR CONVERSION OF U/Pu NITRATES TO OXIDES Part 1. Laboratory-scale Denitration Studies by S. Vogler, D. E. Grosvenor, N. M. Levitz, and F. G. Teats Chemical Engineering Division April 1972 NOTICE- This report was prepared as an account of work sponsored by the United States Government. Neither the United States nor the United States Atomic Energy Commission, nor any of their employees, nor any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, com• pleteness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. BOTBimON DF THIS DOCUMENT IS ONLI DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency Thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. -

Electron Probe Microanalysis
Electron probe microanalysis Essential Knowledge Briefings First Edition, 2015 2 ELECTRON PROBE MICROANALYSIS Front cover image: high-resolution X-ray maps of copper (Cu), zinc (Zn) and silver (Ag) illustrating the interdiffusion zone between the main material (Cu) and the brazing material (Ag-Zn). Data acquired with the SXFiveFE at 10keV, 30nA © 2015 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, UK Microscopy EKB Series Editor: Dr Julian Heath Spectroscopy and Separations EKB Series Editor: Nick Taylor ELECTRON PROBE MICROANALYSIS 3 CONTENTS 4 INTRODUCTION 6 HISTORY AND BACKGROUND 13 IN PRACTICE 22 PROBLEMS AND SOLUTIONS 28 WHAT’S NEXT? About Essential Knowledge Briefings Essential Knowledge Briefings, published by John Wiley & Sons, comprise a series of short guides to the latest techniques, appli - cations and equipment used in analytical science. Revised and updated annually, EKBs are an essential resource for scientists working in both academia and industry looking to update their understanding of key developments within each specialty. Free to download in a range of electronic formats, the EKB range is available at www.essentialknowledgebriefings.com 4 ELECTRON PROBE MICROANALYSIS INTRODUCTION Electron probe microanalysis (EPMA) is an analytical technique that has stood the test of time. Not only is EPMA able to trace its origins back to the discovery of X-rays at the end of the nineteenth century, but the first commercial instrument appeared over 50 years ago. Nevertheless, EPMA remains a widely used technique for determining the elemental composition of solid specimens, able to produce maps showing the distribution of elements over the surface of a specimen while also accurately measuring their concentrations. -

Application of Laser-Induced Breakdown Spectroscopy to Forensic Science: Analysis of Paint Samples
The author(s) shown below used Federal funds provided by the U.S. Department of Justice and prepared the following final report: Document Title: Application of Laser-Induced Breakdown Spectroscopy to Forensic Science: Analysis of Paint Samples Author: Michael E. Sigman, Ph.D., Erin M. McIntee, M.S., Candice Bridge, Ph.D. Document No.: 237839 Date Received: February 2012 Award Number: 2006-DN-BX-K251 This report has not been published by the U.S. Department of Justice. To provide better customer service, NCJRS has made this Federally- funded grant final report available electronically in addition to traditional paper copies. Opinions or points of view expressed are those of the author(s) and do not necessarily reflect the official position or policies of the U.S. Department of Justice. This document is a research report submitted to the U.S. Department of Justice. This report has not been published by the Department. Opinions or points of view expressed are those of the author(s) and do not necessarily reflect the official position or policies of the U.S. Department of Justice. FINAL TECHNICAL REPORT Application of Laser-Induced Breakdown Spectroscopy to Forensic Science: Analysis of Paint Samples Michael E. Sigman, Ph.D. (Principal Investigator) Erin M. McIntee, M.S. Candice Bridge, Ph.D. 1National Center for Forensic Science and Department of Chemistry, University of Central Florida, PO Box 162367, Orlando, FL 32816-2367 Award number 2006-DN-BX-K251 Office of Justice Programs National Institute of Justice Department of Justice Points of view in this document are those of the authors and do not necessarily represent the official position of the U.S. -

The Electron Microprobe Laboratory at Arizona State University
47th Lunar and Planetary Science Conference (2016) 3018.pdf THE ELECTRON MICROPROBE LABORATORY AT ARIZONA STATE UNIVERSITY. A. Wittmann1, D. Convey1, T. Sharp1, M. Wadhwa2, P. Buseck3, and K. Hodges4 1LeRoy Eyring Center for Solid State Science, Arizona State University, Box 871704, Tempe, AZ 85287-1704, [email protected]; 2Center for Meteorite Studies-School of Earth and Space Exploration, Arizona State University, Box 871404, Tempe, AZ 85287; 3School of Molecular Sciences, Arizona State University, Box 871604, Tempe, AZ 85287-1604; 4School of Earth and Space Exploration, Arizona State University, Box 876004, Tempe, AZ 85287-6004. Introduction: In 2011, Arizona State University For instrument control, we can utilize the custom- replaced their 25 year old electron microprobe with a ized JEOL system software and the PC-based Probe state-of-the-art JEOL JXA-8530F field emission in- for Windows software. strument. Our facility was partially funded by NASA Summary Analytical Capabilities: The electron and serves as an investigator facility instrument for microprobe laboratory at Arizona State University NASA’s Planetary Science Research Program. allows to determine the chemical composition of solid Technical Capacities: The JEOL JXA-8530F materials up to 10 cm in size that are stable under high HyperProbe is an electron microscope that has a nomi- vacuum. The non-destructive analytical technique does nal imaging resolution of 3 nm with a X-ray spectrom- not require special sample preparation and produces eter for non-destructive X-ray -

Duncumb: Microprobe Design in the 1950S: Some Examples in Europe
Microsc. Microanal. 7, 100–107, 2001 DOI: 10.1007/s100050010068 Microscopy AND Microanalysis © MICROSCOPY SOCIETY OF AMERICA 2001 Microprobe Design in the 1950s: Some Examples in Europe Peter Duncumb* Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge CB2 3EQ, UK Abstract: The early days of the electron microprobe were characterized by the variety of designs emerging from different laboratories in Europe, the United States, and the USSR. Examples from Europe illustrate well the diverging trends in the evolutionary process at that time. Later, commercial pressures and a better understand- ing of user needs forced a rationalization on both sides of the Atlantic, to the point where only few variants have survived. These were memorable days, with scope for healthy rivalry and vigorous debate. Key words: electron microprobe, magnetic lens design, X-ray spectrometers, microprobe analysis, X-ray mi- croanalysis, instrument design INTRODUCTION Nearly all were represented at a memorable meeting in 1958 in Washington, DC, organized by LaVerne Birks of In this commemoration of 50 years of microprobe analysis, the Naval Research Laboratory, who was himself one of I shall look back to the first decade, before the technique the early pioneers in the US. became commercialized in the 1960s. Papers in this issue by 2. To show how the design of these instruments was influ- Jean Philibert, Kurt Heinrich, and others introduce the enced by the particular applications for which they were broad dimension, so I can concentrate on a relatively nar- intended, and by the interests and background of the row aspect of the history: the evolution of instrument de- designer. -

Raman Microprobe in the Study of Iron Technique; and Steel* a New
UDC 543.423.8 :535.374 Laser Raman Microprobe Technique; A New Analytical Tool in the Study of Iron and Steel* By Kimitaka SATO** Synopsis It may be said that such background has naturally In recentyears, the laser Raman microprobetechnique has attracted the led to the development of a new microbeam analysis attention of many researchers as a new analytical techniquefor local ap- method, called the laser Raman microprobe,s-11) to plication. This paper introducesthe principle, function andfeatures of the obtain the information about the chemical bonds or technique and discusses its applicability to the study of iron and steel, conformation of molecules in local areas. Attempts citing several examples of application. This technique is based on phe- were made to apply the laser Raman microprobe to nomenon,called the Roman scattering, which is caused when a sample is the analysis of defects in materials, inclusions in min- irradiated with a laser light focussed to the utmost. The advantage of erals, catalysts, samples for environmental control this techniqueover conventionalones is that it is capable of obtaining the information about chemical species and atomic groups of moleculesin local and biological samples. In 1978, the 6th Interna- areas (~ rcm) through point, line or image (Raman image of specific tional Conference on Raman Spectroscopy was held wavenumber) analysis. Although this technique has notyet been applied in Bangalore, India, a place noted in connection with widely in the study of iron and steel, the scope of its application will be Raman, in commemoration of the 50th anniversary greatly widenedas a powerful tool in the elucidation of local defects, such of the discovery of the Raman effect.12) At this con- as blisters,precibitates, inclusion'sand corrosionproducts. -

Scanning Electron Probe Microanalysis
1 Reference book not to be 1 1967 NBS TECHNICAL NOTE 278 Scanning Electron Probe Microanalysis KURT F. J. HEINRICH 7 > Si,? o U.S. DEPARTMENT OF COMMERCE 10 National Bureau of Standards Q \ ^ **CAU 0? — THE NATIONAL BUREAU OF STANDARDS The National Bureau of Standards 1 provides measurement and technical information services essential to the efficiency and effectiveness of the work of the Nation's scientists and engineers. The Bureau serves also as a focal point in the Federal Government for assuring maximum application of the physical and engineering sciences to the advancement of technology in industry and commerce. To accomplish this mission, the Bureau is organized into three institutes covering broad program areas of research and services: THE INSTITUTE FOR BASIC STANDARDS . provides the central basis within the United States for a complete and consistent system of physical measurements, coordinates that system with the measurement systems of other nations, and furnishes essential services leading to accurate and uniform physical measurements throughout the Nation's scientific community, industry, and commerce. This Institute comprises a series of divisions, each serving a classical subject matter area: —Applied Mathematics—Electricity—Metrology—Mechanics—Heat—Atomic Physics—Physical Chemistry—Radiation Physics—Laboratory Astrophysics 2—Radio Standards Laboratory, 2 which includes Radio Standards Physics and Radio Standards Engineering—Office of Standard Refer- ence Data. THE INSTITUTE FOR MATERIALS RESEARCH . conducts materials research and provides associated materials services including mainly reference materials and data on the properties of ma- terials. Beyond its direct interest to the Nation's scientists and engineers, this Institute yields services which are essential to the advancement of technology in industry and commerce.