DOCSLIB.ORG

From 3D to 2D: Orthographic and Perspective Projection—Part 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
From 3D to 2D: Orthographic and Perspective Projection—Part 1 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS From 3D to 2D: Orthographic and Perspective Projection—Part 1 Drawing as Projection • A painting based on a mythical tale as told by Pliny the Elder: a Corinthian maiden traces the shadow of her departing lover. • History • Geometrical Constructions • Types of Projection • Projection in Computer Graphics detail from The Invention of Drawing, 1830: Karl Friedrich Schinkle (Mitchell p.1) Andries van Dam September 17, 1998 3D Viewing I 1/31 Andries van Dam September 17, 1998 3D Viewing I 2/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Early Examples of Projection Early Perspective • Plan from Mesopotamia, 2150BC is earliest • Ways of invoking three dimensional space: known technical drawing in existence. rounded, volumetric forms suggested by shading, spatial depth of room suggested by • Greek vases from late 6th century BC show converging lines. perspective(!) • Not systematic—lines do not converge to a • Vitruvius, a Roman architect published single “vanishing” point. specifications of plan and elevation drawings, and perspective. Illustrations for these writings have been lost. Giotto, Confirmation of the rule of Saint Francis, c.1325 (Kemp p.8) Carlbom Fig. 1-1 Andries van Dam September 17, 1998 3D Viewing I 3/31 Andries van Dam September 17, 1998 3D Viewing I 4/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Setting for “Invention” of Brunelleschi Perspective Projection • Invented systematic method of determining perspective projections in early 1400’s. • The Renaissance: new emphasis on Evidence that he created demonstration importance of individual point of view and panels, with specific viewing constraints for interpretation of world, power of complete accuracy of reproduction. observation— particularly of nature (astronomy, anatomy, botany, etc.). – Massaccio – Donatello – Leonardo – Newton • Universe as clockworks: intellectual rebuilding of universe along mechanical lines. painting mirror Filippo Brunelleschi (1377-1446) Kemp pp.12,13 Andries van Dam September 17, 1998 3D Viewing I 5/31 Andries van Dam September 17, 1998 3D Viewing I 6/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Alberti The Visual Pyramid and Similar • Published first treatise on perspective, Della Triangles Pittura, in 1435. • “A painting is the intersection of a visual • Projected image is easy to calculate. Based on pyramid at a given distance, with a fixed – height of object (AB) – distance from eye to object (CB) center and a defined position of light, – distance from eye to picture plane (CD) represented by art with lines and colors on a – and using the relationship CB : CD as AB : ED given surface.” (Alberti, On Painting pp.32- 33) A’ A picture plane E object projected object eye C D B CB : CD as AB : ED • AB is the component of A’ in the plane of the Leono Battista Alberti (1404-1472) projection Andries van Dam September 17, 1998 3D Viewing I 7/31 Andries van Dam September 17, 1998 3D Viewing I 8/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Las Meninas (1656) by Diego Dürer Velàzquez • Concept of similar triangles described both • Point of view influences content and meaning geometrically and mechanically in widely of what is seen. read treatise by Albrecht Dürer (1471-1528). • Are royal couple in mirror about to enter room? Or is their image a reflection of the painting on the far left? • Analysis through computer reconstruction of the painted space. Albrecht Dürer, Artist Drawing a Lute, 1525 Andries van Dam September 17, 1998 3D Viewing I 9/31 Andries van Dam September 17, 1998 3D Viewing I 10/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Piero della Francesca Geometrical Construction of The Resurrection (1460) Projections • Perspective can be used in an unnatural way to control perception. • Use of two points of view concentrates viewer’s attention alternately on face of Christ and sarcophagus. from Vredeman de Vries’s Perspective, Kemp p.117 Andries van Dam September 17, 1998 3D Viewing I 11/31 Andries van Dam September 17, 1998 3D Viewing I 12/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Planar Geometric Projection Main Classes of Planar • Projectors are straight lines Geometric Projections • Projection surface is a plane( picture plane, a) Perspective: determined by Center of projection plane) Projection (COP) (in our diagrams the “eye”) b) Parallel: determined by Direction of Projection (DOP) (projectors are parallel—do not converge to an “eye” or COP) projectors A A Projectors A© Projectors A© B B B© B© eye, or Projection Projection plane Center of plane Center of Projection projection Center of projection (COP) projectors at infinity picture (a) (b) plane This drawing itself is a perspective projection. Andries van Dam September 17, 1998 3D Viewing I 13/31 Andries van Dam September 17, 1998 3D Viewing I 14/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Logical Relationship Between Types of Projection Types of Projections Planar geometric projections Parallel Perspective Orthographic Oblique One-point Top Cabinet Two-point (plan) Front Axonometric Cavalier Three-point elevation Side elevation Other Isometric Other Andries van Dam September 17, 1998 3D Viewing I 15/31 Andries van Dam September 17, 1998 3D Viewing I 16/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Multiview Orthographic Axonometric Projections • Used for: • Same method as multiview – engineering drawings of machines, machine parts orthographic projections, – working architectural drawings except projection plane • Pros: not parallel to any of the dimetric – accurate measurement possible coordinate planes. Parallel – all views are at same scale lines are equally • Cons: foreshortened. dimetric – does not provide “realistic” view or sense of 3D form • Isometric: Angles between • Usually need multiple views to get a three- all three principal axes are o dimensional feeling for object. equal (120 ). The same scale ratio applies along each isometric Projection axis. plane (top view) • Dimetric: Angles between Projectors for two of the principal axes are dimetric side view equal. Two scale ratios are Projectors for top view needed. • Trimetric: Angles different orthographic between the three principal Projection plane axes. Three scale ratios Projectors for (side view) required. front view Carlbom Fig.3-8 Projection • Note: different names for different views, but plane (front view) all part of a continuum of parallel projections of the cube. Andries van Dam September 17, 1998 3D Viewing I 17/31 Andries van Dam September 17, 1998 3D Viewing I 18/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Isometric Projection Oblique Projections • Used for: • Projectors are at an oblique angle to the – catalogue illustrations projection plane. View cameras have – patent office records accordion housing, used for skyscrapers. – furniture design – structural design • Pros: • Pros: – can present the exact shape of one face of an object (can take accurate measurements): better for elliptical – don’t need multiple views shapes than axonometric projections, better for – illustrates 3D nature of object “mechanical” viewing – measurements can be made to scale along principal – lack of perspective foreshortening makes comparison axes. of sizes easier • Cons: – displays some of bject’s three-dimensional appearance – lack of foreshortening creates distorted appearance. • Cons: – more useful for rectangular than curved shapes. – objects can look distorted if careful choice not made about position of projection plane (e.g., circles become Projection ellipses) plane – lack of foreshortening (not realistic looking) y o o 120 120 Projection y Projector plane Projection- plane x normal Projector x z z 120o Construction of an Example Carlbom Fig.2.2 isometric projection Projection-plane normal (Carlbom Fig. 2-6) Construction of an Example: plan oblique projection of a city oblique parallel projection Andries van Dam September 17, 1998 3D Viewing I 19/31 Andries van Dam September 17, 1998 3D Viewing I 20/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Example: Oblique View Main Types of Oblique • Rules for placing projection plane for oblique Projections views: Projection plane should be chosen according to one or several of the followings: • Cavalier: Angle between projectors and – it is parallel to the most irregular of the principal faces, projection plane is 45o. Perpendicular faces or to the one which contains circular or curved are projected at full scale. surfaces – it is parallel to the longest principal face of the object – it is parallel to the face of interest 1 1 1 1 1 1 o o 30 cavalier projection 45 of unit cube • Cabinet: Angle between projectors and Projection plane parallel to circular face projection plane is arctan(2) = 63.4o. Perpendicular faces are projected at 50% scale. 1 1 1/2 1/2 1 1 Projection plane not parallel to circular face o o 45 30 cabinet projection of unit cube Andries van Dam September 17, 1998 3D Viewing I 21/31 Andries van Dam September 17, 1998 3D Viewing I 22/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Examples of Orthographic and Summary of Parallel Projections Oblique Projections • Assume object face of interest lies in principal plane, i.e., parallel to xy, yz or zx planes. (DOP = Direction of Projection, VPN = View Plane
Load more

Recommended publications
  • CHAPTER 6 PICTORIAL SKETCHING 6-1Four Types of Projections
    CHAPTER 6 PICTORIAL SKETCHING 6-1Four Types of Projections Types of Projections 6-2 Axonometric Projection As shown in figure below, axonometric projections are classified as isometric projection (all axes equally foreshortened), dimetric projection (two axes equally shortened), and trimetric projection (all three axes foreshortened differently, requiring different scales for each axis). (cont) Figures below show the contrast between an isometric sketch (i.e., drawing) and an isometric projection. The isometric projection is about 25% larger than the isometric projection, but the pictorial value is obviously the same. When you create isometric sketches, you do not always have to make accurate measurements locating each point in the sketch exactly. Instead, keep your sketch in proportion. Isometric pictorials are great for showing piping layouts and structural designs. Step by Step 6.1. Isometric Sketching 6-4 Normal and Inclined Surfaces in Isometric View Making an isometric sketch of an object having normal surfaces is shown in figure below. Notice that all measurements are made parallel to the main edges of the enclosing box – that is, parallel to the isometric axes. (cont) Making an isometric sketch of an object that has inclined surfaces (and oblique edges) is shown below. Notice that inclined surfaces are located by offset, or coordinate measurements along the isometric lines. For example, distances E and F are used to locate the inclined surface M, and distances A and B are used to locate surface N. 6-5 Oblique Surfaces in Isometric View Oblique surfaces in isometric view may be drawn by finding the intersections of the oblique surfaces with isometric planes.
    [Show full text]
  • Technical Drawing School of Art, Design and Architecture Sarah Adeel | Nust – Spring 2011 the Ability to ’Document Imagination’
    technical drawing school of art, design and architecture sarah adeel | nust – spring 2011 the ability to ’document imagination’. a mean to design reasoning spring 2011 perspective drawings technical drawing - perspective What is perspective drawing? Perspective originally comes from Latin word per meaning “through” and specere which means “to look.” These are combined to mean “to look through” or “to look at.” Intro to technical drawing perspective technical drawing - perspective What is perspective drawing? The “art definition” of perspective specifically describes creating the appearance of distance into our art. With time, the most typical “art definition” of perspective has evolved into “the technique of representing a three-dimensional image on a two-dimensional Intro to technical drawing surface.” perspective technical drawing - perspective What is perspective drawing? Perspective is about establishing “an eye” in art through which the audience sees. By introducing a sense of depth, space and an extension of reality into art is created, enhancing audience’s participation with it. When things appear more real, they become real to the senses. Intro to technical drawing perspective technical drawing - perspective What are the ingredients of perspective drawing? Any form consists of only three basic things: • it has size or amount • it covers distance • it extends in different directions Intro to technical drawing perspective technical drawing - perspective Everyday examples of perspective drawing Photography is an example of perspectives. In photos scenes are captured having depth, height and distance. Intro to technical drawing perspective technical drawing - perspective What is linear perspective drawing? Linear Perspective: Based on the way the human eye sees the world.
    [Show full text]
  • Orthographic and Perspective Projection—Part 1 Drawing As
    I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S From 3D to 2D: Orthographic and Perspective Projection—Part 1 •History • Geometrical Constructions 3D Viewing I • Types of Projection • Projection in Computer Graphics Andries van Dam September 15, 2005 3D Viewing I Andries van Dam September 15, 2005 3D Viewing I 1/38 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Drawing as Projection Early Examples of Projection • Plan view (orthographic projection) from Mesopotamia, 2150 BC: earliest known technical • Painting based on mythical tale as told by Pliny the drawing in existence Elder: Corinthian man traces shadow of departing lover Carlbom Fig. 1-1 • Greek vases from late 6th century BC show perspective(!) detail from The Invention of Drawing, 1830: Karl Friedrich • Roman architect Vitruvius published specifications of plan / elevation drawings, perspective. Illustrations Schinkle (Mitchell p.1) for these writings have been lost Andries van Dam September 15, 2005 3D Viewing I 2/38 Andries van Dam September 15, 2005 3D Viewing I 3/38 1 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Most Striking Features of Linear Early Perspective Perspective • Ways of invoking three dimensional space: shading • || lines converge (in 1, 2, or 3 axes) to vanishing point suggests rounded, volumetric forms; converging lines suggest spatial depth
    [Show full text]
  • Cylindrical Anamorphic Images –A Digital Method of Generation
    ANDRZEJ ZDZIARSKI, MARCIN JONAK* CYLINDRICAL ANAMORPHIC IMAGES –A DIGITAL METHOD OF GENERATION CYFROWA METODA GENEROWANIA ANAMORFICZNYCH OBRAZÓW WALCOWYCH Abstract The aim of this paper is to present a practical construction for some cylindrical anamorphic images. The method is based on the analytic properties of reflective anamorphic image construction – topics which have been discussed in previous papers. This time, the authors deal with the analytical analysis of a transformation that is applied in order to obtain an anamorphic image, and provide an innovative digital notation of the reflective transformation discussed. The analytical model described here allows us to generate a cylindrical anamorphic image of any object that is represented in the form of a set of parametric equations. Some example anamorphic images together with their counter-images reflected in the surface of a cylindrical mirror will be presented here. The method of construction described enables the development of any design project of an anamorphic image in the urban planning environment and within the interiors of public spaces. Keywords: transformation, anamorphic image, visualization of an anamorphic image, reflective cylinder Streszczenie Niniejszy artykuł przedstawia praktyczną metodę konstruowania obrazów anamorficznych w oparciu o własności analityczne dla anamorf refleksyjnych. Praca jest kontynuacją zagadnień związanych z okre- śleniem geometrycznych zasad powstawania obrazów anamorficznych na bazie obrazu rzeczywistego, na- tomiast prezentuje ona analityczne przekształcenie oraz innowacyjny cyfrowy zapis takich obrazów. Tak więc opracowany model analityczny pozwala generować obrazy anamorficzne dowolnych projektowanych obiektów zapisanych w formie równań parametrycznych. Przykładowe anamorfy zaprezentowano wraz z ich obrazami restytuowanymi za pomocą prototypowego zwierciadła walcowego. Powyższe rozwiązania dają możliwość precyzyjnego projektowania obrazów anamorficznych w zurbanizowanej przestrzeni miej- skiej oraz architektonicznych wnętrzach przestrzeni publicznej.
    [Show full text]
  • The Baroque in Games: a Case Study of Remediation
    San Jose State University SJSU ScholarWorks Master's Theses Master's Theses and Graduate Research Spring 2020 The Baroque in Games: A Case Study of Remediation Stephanie Elaine Thornton San Jose State University Follow this and additional works at: https://scholarworks.sjsu.edu/etd_theses Recommended Citation Thornton, Stephanie Elaine, "The Baroque in Games: A Case Study of Remediation" (2020). Master's Theses. 5113. DOI: https://doi.org/10.31979/etd.n9dx-r265 https://scholarworks.sjsu.edu/etd_theses/5113 This Thesis is brought to you for free and open access by the Master's Theses and Graduate Research at SJSU ScholarWorks. It has been accepted for inclusion in Master's Theses by an authorized administrator of SJSU ScholarWorks. For more information, please contact [email protected]. THE BAROQUE IN GAMES: A CASE STUDY OF REMEDIATION A Thesis Presented to The Faculty of the Department of Art History and Visual Culture San José State University In Partial Fulfillment of the Requirements for the Degree Masters of Arts By Stephanie E. Thornton May 2020 © 2020 Stephanie E. Thornton ALL RIGHTS RESERVED The Designated Thesis Committee Approves the Thesis Titled THE BAROQUE IN GAMES: A CASE STUDY OF REMEDIATION by Stephanie E. Thornton APPROVED FOR THE DEPARTMENT OF ART HISTORY AND VISUAL CULTURE SAN JOSÉ STATE UNIVERSITY May 2020 Dore Bowen, Ph.D. Department of Art History and Visual Culture Anthony Raynsford, Ph.D. Department of Art History and Visual Culture Anne Simonson, Ph.D. Emerita Professor, Department of Art History and Visual Culture Christy Junkerman, Ph. D. Emerita Professor, Department of Art History and Visual Culture ABSTRACT THE BAROQUE IN GAMES: A CASE STUDY OF REMEDIATION by Stephanie E.
    [Show full text]
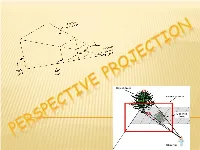
  • Perpective Presentation2.Pdf
    Projections transform points in n-space to m-space, where m<n. Projection is 'formed' on the view plane (planar geometric projection) rays (projectors) projected from the center of projection pass through each point of the models and intersect projection plane. In 3-D, we map points from 3-space to the projection plane (PP) (image plane) along projectors (viewing rays) emanating from the center of projection (COP): TYPES OF PROJECTION There are two basic types of projections: Perspective – center of projection is located at a finite point in three space Parallel – center of projection is located at infinity, all the projectors are parallel Plane geometric projection Parallel Perspective Orthographic Axonometric Oblique Cavalier Cabinet Trimetric Dimetric Single-point Two-point Three-point Isometric PARALLEL PROJECTION • center of projection infinitely far from view plane • projectors will be parallel to each other • need to define the direction of projection (vector) • 3 sub-types Orthographic - direction of projection is normal to view plane Axonometric – constructed by manipulating object using rotations and translations Oblique - direction of projection not normal to view plane • better for drafting / CAD applications ORTHOGRAPHIC PROJECTIONS Orthographic projections are drawings where the projectors, the observer or station point remain parallel to each other and perpendicular to the plane of projection. Orthographic projections are further subdivided into axonom etric projections and multi-view projections. Effective in technical representation of objects AXONOMETRIC The observer is at infinity & the projectors are parallel to each other and perpendicular to the plane of projection. A key feature of axonometric projections is that the object is inclined toward the plane of projection showing all three surfaces in one view.
    [Show full text]
  • Have You Ever Used Two Picture Planes to Draw a Single Perspective View?
    G e n e r a l a r t i c l e have you ever used Two Picture Planes to Draw a Single Perspective View? T o m á S G arc í A S A l gad o Apparently, the use of two picture planes to draw a single view has be a more versatile plane that in addition to representing not been attempted before. Most perspective methods, after Alberti, the appearance of 3D objects would also serve to measure take for granted the use of a single picture plane, disregarding its likely real dimensions? Such a plane, in Modular Perspective [3], use in dual positions. What if two picture planes are necessary to ABSTRACT draw a single view—for example, given a lack of spatial references at can be called the perspective plane (PPL). On the PPL one can ground level to estimate the distance between two objects? This article measure and draw directly the three modular coordinates of demonstrates that to draw the interior of a building from which another all points of interest of any given object in space. In other building can be seen about 190 m away, where the projection of such words, the PPL is a true three-dimensional plane, despite building on the first picture plane would be imprecise, it may be wise to actually being two-dimensional. use a second picture plane. This leads to consideration of how objects In addition, the PPL can be of any size, since all points are change shape as they move away from the viewer.
    [Show full text]
  • From 3D to 2D: Orthographic and Perspective Projection—Part 1
    I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S From 3D to 2D: Orthographic and Perspective Projection—Part 1 • History • Geometrical Constructions • Types of Projection • Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Drawing as Projection • A painting based on a mythical tale as told by Pliny the Elder: a Corinthian man traces the shadow of his departing lover detail from The Invention of Drawing, 1830: Karl Friedrich Schinkle (Mitchell p.1) Andries van Dam September 13, 2001 3D Viewing I 2/34 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Early Examples of Projection • Plan view (orthographic projection) from Mesopotamia, 2150 BC is earliest known technical drawing in existence Carlbom Fig. 1-1 • Greek vases from late 6th century BC show perspective(!) • Vitruvius, a Roman architect, published specifications of plan and elevation drawings, and perspective. Illustrations for these writings have been lost Andries van Dam September 13, 2001 3D Viewing I 3/34 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Most Striking Features of Linear Perspective • || lines converge (in 1, 2, or 3 axes) to a vanishing point • Objects farther away are more foreshortened (i.e., smaller) than closer ones • Example: perspective cube edges same size, with farther ones smaller parallel edges converging Andries van Dam September 13, 2001 3D Viewing I 4/34 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Early Perspective
    [Show full text]
  • Chapter 4 Drawing a Square and Inverse Problems
    Chapter 4 Drawing a square and inverse problems Math 4520, Fall 2017 4.1 Artistic definitions Let us return to our artist painting some object in the picture plane. There is more to the picture than incidence properties such as Desargues' Theorem. In fact, if the artist draws accurately what is seen, things such as Desargues' Theorem will take care of themselves. On the other hand, the picture is a very distorted representation of the object. How distorted can it be? What are some properties that we can measure in the picture that will give us information about the object and how it was painted? We make a few definitions that every artist uses whether he knows it or not. The artist's eye, or center of projection, is called the station point. All the points in the object plane are projected along a straight line through the station point into the picture plane. The line from the station point perpendicular to the picture plane is called the line of sight. The unique point on the line of light in the picture plane is called the center of vision. Note that the center of vision is the nearest point on the picture plane to the station point. Normally one tries to to keep the center of vision near the center of the actual physical painting. The distance between the station point and the center of vision is called the viewing distance. See Figure 4.1 It is usually desirable to keep the viewing distance within some reasonable range. For me 14 inches seems about right.
    [Show full text]
  • Cylindrical Anamorphic Images – a Digital Method of Generation
    ANDRZEJ ZDZIARSKI, MARCIN JONAK* CYLINDRICAL ANAMORPHIC IMAGES –A DIGITAL METHOD OF GENERATION CYFROWA METODA GENEROWANIA ANAMORFICZNYCH OBRAZÓW WALCOWYCH Abstract The aim of this paper is to present a practical construction for some cylindrical anamorphic images. The method is based on the analytic properties of reflective anamorphic image construction – topics which have been discussed in previous papers. This time, the authors deal with the analytical analysis of a transformation that is applied in order to obtain an anamorphic image, and provide an innovative digital notation of the reflective transformation discussed. The analytical model described here allows us to generate a cylindrical anamorphic image of any object that is represented in the form of a set of parametric equations. Some example anamorphic images together with their counter-images reflected in the surface of a cylindrical mirror will be presented here. The method of construction described enables the development of any design project of an anamorphic image in the urban planning environment and within the interiors of public spaces. Keywords: transformation, anamorphic image, visualization of an anamorphic image, reflective cylinder Streszczenie Niniejszy artykuł przedstawia praktyczną metodę konstruowania obrazów anamorficznych w oparciu o własności analityczne dla anamorf refleksyjnych. Praca jest kontynuacją zagadnień związanych z okre- śleniem geometrycznych zasad powstawania obrazów anamorficznych na bazie obrazu rzeczywistego, na- tomiast prezentuje ona analityczne przekształcenie oraz innowacyjny cyfrowy zapis takich obrazów. Tak więc opracowany model analityczny pozwala generować obrazy anamorficzne dowolnych projektowanych obiektów zapisanych w formie równań parametrycznych. Przykładowe anamorfy zaprezentowano wraz z ich obrazami restytuowanymi za pomocą prototypowego zwierciadła walcowego. Powyższe rozwiązania dają możliwość precyzyjnego projektowania obrazów anamorficznych w zurbanizowanej przestrzeni miej- skiej oraz architektonicznych wnętrzach przestrzeni publicznej.
    [Show full text]
  • Perspective Drawing
    Zarqa University Faculty of Engineering Technology Architectural Engineering Department Perspective Drawing Course Information 0901225 Architectural Drawing and Perspective 1 Arch. Dania Abdel-Aziz Perspective Drawing 2 Arch. Dania Abdel-Aziz Perspective Perspective is a geometric method of representing on paper the way that objects appear in real life i.e. they get smaller and closer together the further away they are from the eye of an observer. It is the most realistic of all pictorial drawings. It is is the way real three-dimensional objects are pictured in a photograph that has a two-dimensional plane. Perspective or central projection is used in creative art or technical sketching but seldom in technical drawing. 3 Arch. Dania Abdel-Aziz Projections Projectors or line of sights are not parallel to each other. 4 Arch. Dania Abdel-Aziz Pictorial drawings Perspective drawings differ from other types of pictorial drawings. In Isometric, Dimetric, and Trimetric drawings, the lines remain parallel and never converge at a single point. They are useful for conveying technical information but lack the quality of realism when compared to the perspective view. 5 Arch. Dania Abdel-Aziz Perspective System MAIN ELEMENTS 1. The observer’s eye. 2. The object. 3. The plane of projection. 4. Line of sight. 6 Arch. Dania Abdel-Aziz Perspective System Observer’s eye: is station point (SP). The visual rays: are the line of sights. Picture plane: is the plane of projection or the paper. Visual ray at eye level marks horizon on picture plane. 7 Arch. Dania Abdel-Aziz Vanishing Point The lines parallel to each other but not parallel to the picture plane converge towards a single point on the horizon - VANISHING POINT Notes Observer’s eye is station point SP Visual ray at eye level marks horizon on picture plane.
    [Show full text]
  • Projections & Views
    Projections & views A three-dimensional object can be represented in a single plane, such as on a sheet of paper, by the use of projecting lines and planes. All projection theory is based on two variables: line of sight (projecting lines) and plane of projection. A line of sight (LOS) is an imaginary ray of light between an observer’s eye and an object. A plane of projection (i.e., an image or picture plane) is an imaginary flat plane upon which the image created by the lines of sight is projected. The image is produced by connecting the points where the lines of sight pierce the projection plane. As a result, the 3-D object is transformed into a 2-D representation, also called a projection. If the distance from the observer to the object is infinite, then the projection lines are parallel and the drawing is classified as a parallel projection. Parallel projection is orthographic if the plane of projection is positioned between the observer and the object and is perpendicular to the parallel lines of sight. 1 Parallel projection technique can be used to create both pictorial and multiview drawings. In all these cases all lines of sight are parallel. In multiview projection (orthographic), the object surface & the projection plane are parallel, and only two dimensions can be seen. In oblique projection (non-orthographic) the object surface & the projection plane are also parallel, but the lines of sights are not perpendicular to the projection plane, and three dimensions can be seen. In isometric view (orthographic) the surface is no longer parallel to the projection plane, three dimensions being seen.
    [Show full text]