DOCSLIB.ORG

International System of Units (SI Units)  SI Units  Structure of SI and JIS Z 8203

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
International System of Units (SI Units)  SI Units  Structure of SI and JIS Z 8203 Contact Details Internet Before using the product, please check the http://www.daikinpmc.com/en/ guide pages at the front of this catalog. For latest information, PDF catalogs and operation manuals International System of Units (SI units) SI units Structure of SI and JIS Z 8203 The International System of Units, or SI, comprises seven ⎧ Base units (seven) ｜ base units, prefixes to represent integer powers of 10 in the ｜ 18 −18 ⎧ SI Supplementary units (two) range from 10 to −10 , supplementary units of radians Unit ⎨ ｜ ｜ ⎧Derived units with special names and steradians, and twenty-seven derived units defined ｜ ｜ ⎧ ｜ Derived units (eighteen) SI ⎨ ⎩ ⎨ according to the resolution by the International Committee ｜ ｜ ｜ ｜ Other derived units ｜ ⎩ of Weights and Measures. JIS Z 8203 ⎨ Prefixes (sixteen) and integer powers of 10 of SI units ｜ ⎩ It is often abbreviated as SI from its French expression ｜ "Systeme International d'Unites". ⎩ Important units outside SI - Usable in parallel with SI units Its use in ISO standards started in 1971. In Japan, the Conference on Standardization of the Japanese Industrial Standards Committee decided in 1972 to introduce the SI units to JIS in a stepwise manner. And in 1974, JIS Z 8203 International System of Units (SI) (established based Appendix table 4 Example of SI derived units on ISO1000) and the guide for its use were enacted and that are expressed with special names promulgated, and their dissemination is in progress. Quantity Name Symbol viscosity pascal second Pa·s Appendix table 1 SI base units moment of force newton meter N·m Quantity Name Symbol Quantity Name Symbol surface tension newton per meter N/m heat flux density, length meter m thermodynamic temperature kelvin K watt per square meter W/m2 irradiation mass kilogram kg luminous intensity candela cd heat capacity, entropy joule per kelvin J/K time second s amount of substance mole mol specific heat capacity, joule per kilogram kelvin J/(kg·K) current ampere A specific entropy * thermal conductivity watt per meter kelvin W/(m·K) Appendix table 2 SI supplementary units permittivity farad per meter F/m permeability henry per meter H/m Quantity Name Symbol Plane related angle radian rad * It is also referred to as mass entropy. solid angle steradian sr Table 5 SI prefixes Appendix table 3 SI derived units with special names Multiplication Prefix Symbol Multiplication Prefix Symbol 1018 exa E 10−1 deci d Quantity Name Symbol Definition 1015 peta P 10−2 centi c frequency hertz Hz s−1 1012 tera T 10−3 milli m force newton N m·kg·s−2 109 giga G 10−6 micro μ pressure, stress pascal Pa N/m2 106 mega M 10−9 nano n energy, work, heat joule J N·m 103 kilo k 10−12 pico p power, radiant flux watt W J/s 102 hecto h 10−15 femto f quantity of electricity, coulomb C A·s 1 −18 electric charge 10 deca da 10 atto a voltage, electrical potential volt V W/A Multiplications of 106 (M: mega) and larger are expressed with capital electrical capacitance farad F C/V letters. electrical resistance ohm Ω V/A Appendix table 6 Units used in parallel with SI units conductance siemens S A/V Name Symbol Value in SI units magnetic flux weber Wb V·s minute min 1 min = 60 s magnetic flux density tesla T Wb/m2 hour h 1 h = 60 min = 3,600 s inductance henry H Wb/A day d 1 d = 24 h = 86,400 s celsius' temperature scale degree Celsius * °C t°C = (t + 273.15) K degree ° 1° = (π/180) rad luminous flux lumen lm cd·sr minute ' 1' = (1/60)" = (π/10,800) rad illuminance lux lx 1 second " 1" = (1/60)' = (π/648,000) rad radioactivity becquerel Bq liter L 1 L = 1 dm3 = 10−3 m3 absorbed dose gray Gy ton t 1 t = 103 kg Appendix table 7.1 Conversion table from conventional gravitation units to SI units T Quantity Unit name Symbol Conversion factor SI unit name Symbol degree ° π/180 angle minute ' π/10800 radian rad second " π/648000 meter m 1 length micron μm 10−6 meter m angstrom Å 10−10 square meter m2 1 area square meter m2 are a 102 3 cubic meter m 1 3 volume −3 cubic meter m liter L 10 TECHNICAL SERVICE DATA T-17 Contact Details Internet Before using the product, please check the http://www.daikinpmc.com/en/ guide pages at the front of this catalog. For latest information, PDF catalogs and operation manuals International System of Units (SI units) Appendix table 7.2 Conversion table from conventional gravitation units to SI units Quantity Unit name Symbol Conversion factor SI unit name Symbol degree ° π/180 angle minute ' π/10800 radian rad second " π/648000 meter m 1 length micron μ 10−6 meter m angstrom Å 10−10 square meter m2 1 area square meter m2 are a 102 cubic meter m3 1 volume cubic meter m3 liter l, L 10−3 kilogram kg 1 mass ton t 103 kilogram kg atomic mass unit u 1.6606 × 10−27 second s 1 minute min 60 time second s hour h 3600 day d 86400 speed, velocity meter per second m/s 1 meter per second m/s frequency cycle s−1 1hertz Hz rotational speed times per minute min−1 1/60 revolutions per second s−1 angular velocity radian per second rad/s 1 radian per second rad/s meter per second squared m/s2 1 meter per acceleration m/s2 g G 9.8067 second squared weight kilogram kgf 9.8067 force weight ton tf 9806.7 newton N dyne dyn 10−5 moment of force weight kilogram meter kgf·m 9.8067 newton meter N·m weight kilogram per square meter kgf/m2 9.8067 stress weight kilogram per square centimeter kgf/cm2 9.8067 × 104 pascal Pa weight kilogram per square millimeter kgf/mm2 9.8067 × 106 weight kilogram per square meter kgf/m2 9.8067 meter of water mH O 9806.7 pressure 2 pascal Pa millimeter mercury column mmHg 101325/760 bar bar 105 erg erg 10−7 International Steam Table calorie calIT 4.1868 energy weight kilogram meter kgf·m 9.8067 joule J kilowatt hour kW·h 3.600 × 106 metric horse power hour PS·h 2.6478 × 106 watt W 1 work rate and power metric horse power PS 735.5 watt W kilocalorie per hour kcal/h 1.163 poise P 10−1 viscosity and viscosity centipoise cP 10−3 pascal second Pa·s coefficient weight kilogram second per square meter kgf·s/m2 9.8067 dynamic viscosity and stokes St 10−4 square meter dynamic viscosity m2/s centistokes mm2/S, cSt 10−6 per second coefficient temperature degree °C +273.15 kelvin K −8 magnetic flux maxwell MX 10 weber Wb gamma γ 10−9 magnetic flux density −4 tesla T gauss GS 10 3 π magnetic field strength oersted Oe 10 /4 ampere per meter A/m quantity of electricity coulomb C 1 coulomb C electrical potential volt V 1 volt V difference electrical capacitance farad F 1 farad F electrical resistance ohm Ω 1ohm Ω conductance siemens S 1 siemens S inductance henry H 1 henry H current ampere A 1 ampere A T-18 Contact Details Internet Before using the product, please check the http://www.daikinpmc.com/en/ guide pages at the front of this catalog. For latest information, PDF catalogs and operation manuals Appendix table 8 Comparison table between SI and CGS/system of gravitational units Absolute system of units Gravity unit system Representative quantity SI units m - kg ft - lb m - kgf ft - lbf length m m ft m ft mass kg kg lb kgf·s2/m lbf·s2/ft timesssss gravity (force) N kg·m/s2 lb·ft/s2 kgf lbf acceleration m/s2 m/s2 ft/s2 kgf/s2 lbf/s2 pressure (stress) Pa kg/m·s2 lb/ft·s2 kgf/m2 lbf/ft2 energy J kg·m2/s2 lb·ft2/s2 kgf·m lbf/ft work rate W kg·m2/s3 lb·ft2/s3 kgf·m/s lbf·ft/s density kg/m3 kg/m3 lb/ft3 kgf·s2/m4 lbf·s2/ft4 viscosity Pa·s kg/m·s lb/ft·s kgf·s/m2 lbf·s/ft2 temperature K °C °C °C °C Note: 1 N = 105 g·cm/s2, 1 Pa = IN/m2, 1J = 1 N·m, 1 W = 1 N·m/s 1 dyn = 1 g·cm/s2, 1 Poundal = 1 lb·ft/s2, 1 slug = 1 lb·s2/ft 1 Poise = 1 g/cm·s T TECHNICAL SERVICE DATA T-19 Contact Details Internet Before using the product, please check the http://www.daikinpmc.com/en/ guide pages at the front of this catalog. For latest information, PDF catalogs and operation manuals International System of Units (SI units) Conversion tables for frequently used units to SI units Force Moment of force N N·m dyn kgf kgf·m newton newton meter 1 1 × 105 1.019 72 × 10−1 1 0.102 0 1 × 10−5 1 1.019 72 × 10−6 9.807 1 5 9.806 65 9.806 65 × 10 1 2 Note: 1 N·m = 1 kg·m /S2 Pressure Viscosity 2 mmHg or Pa·s Pa bar kgf/cm atm mmH2O cP P (poise) Torr pascal second × −5 × −5 × −6 × −1 × −3 1 1 10 1.019 72 10 9.869 23 10 1.019 72 10 7.500 62 10 1 1 × 103 1 × 10 × 5 × −1 × 4 × 2 1 10 1 1.019 72 9.869 23 10 1.019 72 10 7.500 62 10 1 × 10−3 1 1 × 10−2 × 4 × −1 × −1 × 4 × 2 9.806 65 10 9.806 65 10 1 9.678 41 10 1 10 7.355 59 10 1 × 10−1 1 × 102 1 1.013 25 × 105 1.013 25 1.033 23 1 1.033 23 × 104 7.600 00 × 102 Note: 1 P = 1 dyn·s/cm2 = 1 g/cm·s − − − − 9.806 65 9.806 65 × 10 5 1 × 10 4 9.678 41 × 10 5 1 7.355 59 × 10 2 1 Pa·s = 1 N·s/m2, 1 cP = 1 mPa·s 1.333 22 × 102 1.333 22 × 10−3 1.359 51 × 10−3 1.315 79 × 10−3 1.359 51 × 10 1 Note: 1 Pa = 1 N/m2 Dynamic viscosity 2 2 Stress m /S mm /S St 2 2 2 Pa MPa or N/mm kgf/mm kgf/cm 1 1 × 106 1 × 104 1 × 10−6 1 1 × 10−2 1 1 × 10−6 1.019 72 × 10−7 1.019 72 × 10−5 1 × 10−4 1 × 102 1 1 × 106 1 1.019 72 × 10−1 1.019 72 × 10 9.806 65 × 106 9.806 65 1 1 × 102 Note: 1 St = 1 cm2/s 9.806 65 × 104 9.806 65 × 10−2 1 × 10−2 1 Thermal conductivity Work, Energy, Heat W/(m·K) kcal/(h·m·°C) JkW·hkgf·mkcal 1 8.600 0 × 10−1 1 2.777 78 × 10−7 1.019 72 × 10−1 2.388 89 × 10−4 1.162 79 1 3.600 × 106 1 3.670 98 × 105 8.600 0 × 102 Note: 1 cal = 4.186 05 J 9.806 65 2.724 07 × 10−6 1 2.342 70 × 10−3 4.186 05 × 103 1.162 79 × 10−3 4.268 58 × 102 1 Heat transfer coefficient Note: 1 J = 1 W·s, 1 W·h3 600 W·s 1 cal = 4.186 05 J W/(m2·K) kcal/(h·m2·°C) Power 1 8.600 0 × 10−1 kW kgf·m/s PS kcal/h 1.162 79 1 1 1.019 72 × 102 1.359 62 8.600 0 × 102 Note: 1 cal = 4.186 05 J 9.806 65 × 10−3 1 1.333 33 × 10−2 8.433 71 7.355 × 10−1 7.5 × 10 1 6.325 29 × 102 Specific heat capacity 1.162 79 × 10−3 1.185 72 × 10−1 1.580 95 × 10−3 1 kcal/(kg·°C) J/(kg·K) Note: 1 W = 1 J/s, PS: metric horsepower cal/(g·°C) 1 PS = 0.735 5 kW 1 cal = 4.186 05 J 1 2.388 89 × 10−4 4.186 05 × 103 1 Temperature Note: 1 cal = 4.186 05 J T1 = T2 + 273.15 T3 = 1 .
Load more

Recommended publications
  • Foundations of Newtonian Dynamics: an Axiomatic Approach For
    Foundations of Newtonian Dynamics: 1 An Axiomatic Approach for the Thinking Student C. J. Papachristou 2 Department of Physical Sciences, Hellenic Naval Academy, Piraeus 18539, Greece Abstract. Despite its apparent simplicity, Newtonian mechanics contains conceptual subtleties that may cause some confusion to the deep-thinking student. These subtle- ties concern fundamental issues such as, e.g., the number of independent laws needed to formulate the theory, or, the distinction between genuine physical laws and deriva- tive theorems. This article attempts to clarify these issues for the benefit of the stu- dent by revisiting the foundations of Newtonian dynamics and by proposing a rigor- ous axiomatic approach to the subject. This theoretical scheme is built upon two fun- damental postulates, namely, conservation of momentum and superposition property for interactions. Newton’s laws, as well as all familiar theorems of mechanics, are shown to follow from these basic principles. 1. Introduction Teaching introductory mechanics can be a major challenge, especially in a class of students that are not willing to take anything for granted! The problem is that, even some of the most prestigious textbooks on the subject may leave the student with some degree of confusion, which manifests itself in questions like the following: • Is the law of inertia (Newton’s first law) a law of motion (of free bodies) or is it a statement of existence (of inertial reference frames)? • Are the first two of Newton’s laws independent of each other? It appears that
    [Show full text]
  • A Concurrent PASCAL Compiler for Minicomputers
    512 Appendix A DIFFERENCES BETWEEN UCSD'S PASCAL AND STANDARD PASCAL The PASCAL language used in this book contains most of the features described by K. Jensen and N. Wirth in PASCAL User Manual and Report, Springer Verlag, 1975. We refer to the PASCAL defined by Jensen and Wirth as "Standard" PASCAL, because of its widespread acceptance even though no international standard for the language has yet been established. The PASCAL used in this book has been implemented at University of California San Diego (UCSD) in a complete software system for use on a variety of small stand-alone microcomputers. This will be referred to as "UCSD PASCAL", which differs from the standard by a small number of omissions, a very small number of alterations, and several extensions. This appendix provides a very brief summary Of these differences. Only the PASCAL constructs used within this book will be mentioned herein. Documents are available from the author's group at UCSD describing UCSD PASCAL in detail. 1. CASE Statements Jensen & Wirth state that if there is no label equal to the value of the case statement selector, then the result of the case statement is undefined. UCSD PASCAL treats this situation by leaving the case statement normally with no action being taken. 2. Comments In UCSD PASCAL, a comment appears between the delimiting symbols "(*" and "*)". If the opening delimiter is followed immediately by a dollar sign, as in "(*$", then the remainder of the comment is treated as a directive to the compiler. The only compiler directive mentioned in this book is (*$G+*), which tells the compiler to allow the use of GOTO statements.
    [Show full text]
  • Pressure, Its Units of Measure and Pressure References
    _______________ White Paper Pressure, Its Units of Measure and Pressure References Viatran Phone: 1‐716‐629‐3800 3829 Forest Parkway Fax: 1‐716‐693‐9162 Suite 500 [email protected] Wheatfield, NY 14120 www.viatran.com This technical note is a summary reference on the nature of pressure, some common units of measure and pressure references. Read this and you won’t have to wait for the movie! PRESSURE Gas and liquid molecules are in constant, random motion called “Brownian” motion. The average speed of these molecules increases with increasing temperature. When a gas or liquid molecule collides with a surface, momentum is imparted into the surface. If the molecule is heavy or moving fast, more momentum is imparted. All of the collisions that occur over a given area combine to result in a force. The force per unit area defines the pressure of the gas or liquid. If we add more gas or liquid to a constant volume, then the number of collisions must increase, and therefore pressure must increase. If the gas inside the chamber is heated, the gas molecules will speed up, impact with more momentum and pressure increases. Pressure and temperature therefore are related (see table at right). The lowest pressure possible in nature occurs when there are no molecules at all. At this point, no collisions exist. This condition is known as a pure vacuum, or the absence of all matter. It is also possible to cool a liquid or gas until all molecular motion ceases. This extremely cold temperature is called “absolute zero”, which is -459.4° F.
    [Show full text]
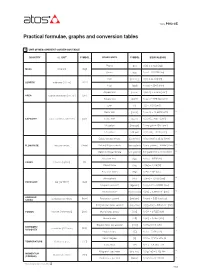
  • Practical Formulae, Graphs and Conversion Tables
    Table P003-4/E Practical formulae, graphs and conversion tables 1 UNIT OF MEASUREMENT CONVERSION TABLE QUANTITY S.I. UNIT SYMBOL OTHER UNITS SYMBOL EQUIVALENCE Pound [lb] 1 [lb] = 0,4536 [kg] kilogram [kg] MASS Ounce [oz] 1 [oz] = 0,02335 [kg] Inch [in] or [”] 1 [in] = 25,40 [mm] millimeter [10-3 m] [mm] LENGTH Foot [foot] 1 [foot] = 304,8 [mm] Square inch [sq in] 1 [sq in] = 6,4516 [cm2] -4 2 [cm2] AREA square centimeter [10 m ] Square foot [sq ft] 1 [sq ft] = 929,034 [cm2] Liter [l] 1 [l] = 1000 [cm3] Cubic inch [cu in] 1 [cu in] = 16,3870 [cm3] * cubic centimeter [10-6 m3] [cm3] Cubic foot [cu ft] 1 [cu ft] = 28317 [cm3] CAPACITY UK gallon [Imp gal] 1 [Imp gal] = 4546 [cm3] US gallon [US gal] 1 [US gal] = 3785 [cm3] * Cubic foot per minute [cu ft/min] 1 [cu ft/min] = 28,32 [l/min] liter per minute [l/min] Gallon (UK) per minute [Imp gal/min] 1 [Imp gal/min] = 4,5456 [l/min] * FLOW RATE Gallon (US) per minute [US gal/min] [US gal/min] = 3,7848 [l/min] * Kilogram force [kgf] 1 [kgf] = 9,806 [N] Newton [kgm/s2] [N] FORCE Pound force [lbf] 1 [lbf] = 4,448 [N] Pascal [1 N/m2] [Pa] 1 [Pa] = 10-5 [bar] Atmosphere [atm] 1 [atm] = 1,0132 [bar] * bar [105 N/m2] [bar] PRESSURE 2 2 2 Kilogram force/cm [kgf/cm ] 1 [kgf/cm ] = 0,9806 [bar] 2 2 -2 Pound force/in [lbf /in ] or [psi] 1 [psi] = 6,8948•10 [bar] * ANGULAR revolution per minute [rpm] Radian per second [rad/sec] 1 [rpm] = 9,55 [rad/sec] SPEED -3 Kilogram per meter second [kgf •m/s] 1 [kgf •m/s] = 9,803•10 [kW] kilowatt [1000 Nm/s] [kW] Metric horse power [CV] 1 [CV] = 0,7355 [kW] POWER
    [Show full text]
  • American and BRITISH UNITS of Measurement to SI UNITS
    AMERICAN AND BRITISH UNITS OF MEASUREMENT TO SI UNITS UNIT & ABBREVIATION SI UNITS CONVERSION* UNIT & ABBREVIATION SI UNITS CONVERSION* UNITS OF LENGTH UNITS OF MASS 1 inch = 40 lines in 2.54 cm 0.393701 1 grain gr 64.7989 mg 0.0154324 1 mil 25.4 µm 0.03937 1 dram dr 1.77185 g 0.564383 1 line 0.635 mm 1.57480 1 ounce = 16 drams oz 28.3495 g 0.0352739 1 foot = 12 in = 3 hands ft 30.48 cm 0.0328084 1 pound = 16 oz lb 0.453592 kg 2.204622 1 yard = 3 feet = 4 spans yd 0.9144 m 1.09361 1 quarter = 28 lb 12.7006 kg 0.078737 1 fathom = 2 yd fath 1.8288 m 0.546807 1 hundredweight = 112 lb cwt 50.8024 kg 0.0196841 1 rod (perch, pole) rd 5.0292 m 0.198839 1 long hundredweight l cwt 50.8024 kg 0.0196841 1 chain = 100 links ch 20.1168 m 0.0497097 1 short hundredweight sh cwt 45.3592 kg 0.0220462 1 furlong = 220 yd fur 0.201168 km 4.97097 1 ton = 1 long ton tn, l tn 1.016047 t 0.984206 1 mile (Land Mile) mi 1.60934 km 0.62137 1 short ton = 2000 lb sh tn 0.907185 t 1.102311 1 nautical mile (intl.) n mi, NM 1.852 km 0.539957 1 knot (Knoten) kn 1.852 km/h 0.539957 UNITS OF FORCE 1 pound-weight lb wt 4.448221 N 0.2248089 UNITS OF AREA 1 pound-force LB, lbf 4.448221 N 0.2248089 1 square inch sq in 6.4516 cm2 0.155000 1 poundal pdl 0.138255 N 7.23301 1 circular inch 5.0671 cm2 0.197352 1 kilogram-force kgf, kgp 9.80665 N 0.1019716 1 square foot = 144 sq in sq ft 929.03 cm2 1.0764 x 10-4 1 short ton-weight sh tn wt 8.896444 kN 0.1124045 1 square yard = 9 sq ft sq yd 0.83613 m2 1.19599 1 long ton-weight l tn wt 9.964015 kN 0.1003611 1 acre = 4 roods 4046.8
    [Show full text]
  • An Atomic Physics Perspective on the New Kilogram Defined by Planck's Constant
    An atomic physics perspective on the new kilogram defined by Planck’s constant (Wolfgang Ketterle and Alan O. Jamison, MIT) (Manuscript submitted to Physics Today) On May 20, the kilogram will no longer be defined by the artefact in Paris, but through the definition1 of Planck’s constant h=6.626 070 15*10-34 kg m2/s. This is the result of advances in metrology: The best two measurements of h, the Watt balance and the silicon spheres, have now reached an accuracy similar to the mass drift of the ur-kilogram in Paris over 130 years. At this point, the General Conference on Weights and Measures decided to use the precisely measured numerical value of h as the definition of h, which then defines the unit of the kilogram. But how can we now explain in simple terms what exactly one kilogram is? How do fixed numerical values of h, the speed of light c and the Cs hyperfine frequency νCs define the kilogram? In this article we give a simple conceptual picture of the new kilogram and relate it to the practical realizations of the kilogram. A similar change occurred in 1983 for the definition of the meter when the speed of light was defined to be 299 792 458 m/s. Since the second was the time required for 9 192 631 770 oscillations of hyperfine radiation from a cesium atom, defining the speed of light defined the meter as the distance travelled by light in 1/9192631770 of a second, or equivalently, as 9192631770/299792458 times the wavelength of the cesium hyperfine radiation.
    [Show full text]
  • Lord Kelvin and the Age of the Earth.Pdf
    ME201/MTH281/ME400/CHE400 Lord Kelvin and the Age of the Earth Lord Kelvin (1824 - 1907) 1. About Lord Kelvin Lord Kelvin was born William Thomson in Belfast Ireland in 1824. He attended Glasgow University from the age of 10, and later took his BA at Cambridge. He was appointed Professor of Natural Philosophy at Glasgow in 1846, a position he retained the rest of his life. He worked on a broad range of topics in physics, including thermody- namics, electricity and magnetism, hydrodynamics, atomic physics, and earth science. He also had a strong interest in practical problems, and in 1866 he was knighted for his work on the transtlantic cable. In 1892 he became Baron Kelvin, and this name survives as the name of the absolute temperature scale which he proposed in 1848. During his long career, Kelvin published more than 600 papers. He was elected to the Royal Society in 1851, and served as president of that organization from 1890 to 1895. The information in this section and the picture above were taken from a very useful web site called the MacTu- tor History of Mathematics Archive, sponsored by St. Andrews University. The web address is http://www-history.mcs.st-and.ac.uk/~history/ 2 kelvin.nb 2. The Age of the Earth The earth shows it age in many ways. Some techniques for estimating this age require us to observe the present state of a time-dependent process, and from that observation infer the time at which the process started. If we believe that the process started when the earth was formed, we get an estimate of the earth's age.
    [Show full text]
  • Having Regard to the Opinion of the European Chapter 1 of the Annex Binding Within Five Years of Parliament1 ; the Date of Entry Into Force of This Directive
    878 Official Journal of the European Communities 29.10.71 Official Journal of the European Communities No L 243/29 COUNCIL DIRECTIVE of 18 October 1971 on the approximation of the laws of the Member States relating to units of measurement (71/354/EEC ) THE COUNCIL OF THE EUROPEAN COMMUNITIES, particular their names, symbols and use are not identical in the Member countries ; Having regard to the Treaty establishing the European Economic Community, and in particular HAS ADOPTED THIS DIRECTIVE : Article 100 thereof; Article 1 Having regard to the proposal from the Commission ; 1 . Member States shall make the provisions of Having regard to the Opinion of the European Chapter 1 of the Annex binding within five years of Parliament1 ; the date of entry into force of this Directive. 2 . Member States shall, with effect from 31 Having regard to the Opinion of the Economic and December 1977 at the latest, prohibit the use of the Social Committee2; units of measurement listed in Chapter III of the Annex. Whereas - the laws which regulate the use of units of measurement in the Member States differ from one 3 . The units of measurement temporarily" retained Member State to another and therefore hinder trade ; in accordance with the provisions of Chapter II or whereas application of the rules relating to measuring Chapter III of the Annex may not be brought into instruments is closely linked to the use of units of compulsory use by the Member States where they ' are measurement in the metrological system ; whereas, in not authorised at the date when this Directive enters into force .
    [Show full text]
  • Illumination and Distance
    PHYS 1400: Physical Science Laboratory Manual ILLUMINATION AND DISTANCE INTRODUCTION How bright is that light? You know, from experience, that a 100W light bulb is brighter than a 60W bulb. The wattage measures the energy used by the bulb, which depends on the bulb, not on where the person observing it is located. But you also know that how bright the light looks does depend on how far away it is. That 100W bulb is still emitting the same amount of energy every second, but if you are farther away from it, the energy is spread out over a greater area. You receive less energy, and perceive the light as less bright. But because the light energy is spread out over an area, it’s not a linear relationship. When you double the distance, the energy is spread out over four times as much area. If you triple the distance, the area is nine Twice the distance, ¼ as bright. Triple the distance? 11% as bright. times as great, meaning that you receive only 1/9 (or 11%) as much energy from the light source. To quantify the amount of light, we will use units called lux. The idea is simple: energy emitted per second (Watts), spread out over an area (square meters). However, a lux is not a W/m2! A lux is a lumen per m2. So, what is a lumen? Technically, it’s one candela emitted uniformly across a solid angle of 1 steradian. That’s not helping, is it? Examine the figure above. The source emits light (energy) in all directions simultaneously.
    [Show full text]
  • Newton.Indd | Sander Pinkse Boekproductie | 16-11-12 / 14:45 | Pag
    omslag Newton.indd | Sander Pinkse Boekproductie | 16-11-12 / 14:45 | Pag. 1 e Dutch Republic proved ‘A new light on several to be extremely receptive to major gures involved in the groundbreaking ideas of Newton Isaac Newton (–). the reception of Newton’s Dutch scholars such as Willem work.’ and the Netherlands Jacob ’s Gravesande and Petrus Prof. Bert Theunissen, Newton the Netherlands and van Musschenbroek played a Utrecht University crucial role in the adaption and How Isaac Newton was Fashioned dissemination of Newton’s work, ‘is book provides an in the Dutch Republic not only in the Netherlands important contribution to but also in the rest of Europe. EDITED BY ERIC JORINK In the course of the eighteenth the study of the European AND AD MAAS century, Newton’s ideas (in Enlightenment with new dierent guises and interpre- insights in the circulation tations) became a veritable hype in Dutch society. In Newton of knowledge.’ and the Netherlands Newton’s Prof. Frans van Lunteren, sudden success is analyzed in Leiden University great depth and put into a new perspective. Ad Maas is curator at the Museum Boerhaave, Leiden, the Netherlands. Eric Jorink is researcher at the Huygens Institute for Netherlands History (Royal Dutch Academy of Arts and Sciences). / www.lup.nl LUP Newton and the Netherlands.indd | Sander Pinkse Boekproductie | 16-11-12 / 16:47 | Pag. 1 Newton and the Netherlands Newton and the Netherlands.indd | Sander Pinkse Boekproductie | 16-11-12 / 16:47 | Pag. 2 Newton and the Netherlands.indd | Sander Pinkse Boekproductie | 16-11-12 / 16:47 | Pag.
    [Show full text]
  • Electric Units and Standards
    DEPARTMENT OF COMMERCE OF THE Bureau of Standards S. W. STRATTON, Director No. 60 ELECTRIC UNITS AND STANDARDS list Edition 1 Issued September 25. 1916 WASHINGTON GOVERNMENT PRINTING OFFICE DEPARTMENT OF COMMERCE Circular OF THE Bureau of Standards S. W. STRATTON, Director No. 60 ELECTRIC UNITS AND STANDARDS [1st Edition] Issued September 25, 1916 WASHINGTON GOVERNMENT PRINTING OFFICE 1916 ADDITIONAL COPIES OF THIS PUBLICATION MAY BE PROCURED FROM THE SUPERINTENDENT OF DOCUMENTS GOVERNMENT PRINTING OFFICE WASHINGTON, D. C. AT 15 CENTS PER COPY A complete list of the Bureau’s publications may be obtained free of charge on application to the Bureau of Standards, Washington, D. C. ELECTRIC UNITS AND STANDARDS CONTENTS Page I. The systems of units 4 1. Units and standards in general 4 2. The electrostatic and electromagnetic systems 8 () The numerically different systems of units 12 () Gaussian systems, and ratios of the units 13 “ ’ (c) Practical ’ electromagnetic units 15 3. The international electric units 16 II. Evolution of present system of concrete standards 18 1. Early electric standards 18 2. Basis of present laws 22 3. Progress since 1893 24 III. Units and standards of the principal electric quantities 29 1. Resistance 29 () International ohm 29 Definition 29 Mercury standards 30 Secondary standards 31 () Resistance standards in practice 31 (c) Absolute ohm 32 2. Current 33 (a) International ampere 33 Definition 34 The silver voltameter 35 ( b ) Resistance standards used in current measurement 36 (c) Absolute ampere 37 3. Electromotive force 38 (a) International volt 38 Definition 39 Weston normal cell 39 (b) Portable Weston cells 41 (c) Absolute and semiabsolute volt 42 4.
    [Show full text]
  • Paul Hertz Astrophysics Subcommittee
    Paul Hertz Astrophysics Subcommittee February 23, 2012 Agenda • Science Highlights • Organizational Changes • Program Update • President’s FY13 Budget Request • Addressing Decadal Survey Priorities 2 Chandra Finds Milky Way’s Black Hole Grazing on Asteroids • The giant black hole at the center of the Milky Way may be vaporizing and devouring asteroids, which could explain the frequent flares observed, according to astronomers using data from NASA's Chandra X-ray Observatory. For several years Chandra has detected X-ray flares about once a day from the supermassive black hole known as Sagittarius A*, or "Sgr A*" for short. The flares last a few hours with brightness ranging from a few times to nearly one hundred times that of the black hole's regular output. The flares also have been seen in infrared data from ESO's Very Large Telescope in Chile. • Scientists suggest there is a cloud around Sgr A* containing trillions of asteroids and comets, stripped from their parent stars. Asteroids passing within about 100 million miles of the black hole, roughly the distance between the Earth and the sun, would be torn into pieces by the tidal forces from the black hole. • These fragments then would be vaporized by friction as they pass through the hot, thin gas flowing onto Sgr A*, similar to a meteor heating up and glowing as it falls through Earth's atmosphere. A flare is produced and the remains of the asteroid are eventually swallowed by the black hole. • The authors estimate that it would take asteroids larger than about six miles in radius to generate the flares observed by Chandra.
    [Show full text]