Discoveries of Mass Independent Isotope Effects in the Solar System: Past, Present and Future Mark H
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Template for Two-Page Abstracts in Word 97 (PC)
GEOLOGIC MAPPING OF THE LUNAR SOUTH POLE QUADRANGLE (LQ-30). S.C. Mest1,2, D.C. Ber- man1, and N.E. Petro2, 1Planetary Science Institute, 1700 E. Ft. Lowell, Suite 106, Tucson, AZ 85719-2395 ([email protected]); 2Planetary Geodynamics Laboratory, Code 698, NASA GSFC, Greenbelt, MD 20771. Introduction: In this study we use recent image, the surface [7]. Impact craters display morphologies spectral and topographic data to map the geology of the ranging from simple to complex [7-9,24] and most lunar South Pole quadrangle (LQ-30) at 1:2.5M scale contain floor deposits distinct from surrounding mate- [1-7]. The overall objective of this research is to con- rials. Most of these deposits likely consist of impact strain the geologic evolution of LQ-30 (60°-90°S, 0°- melt; however, some deposits, especially on the floors ±180°) with specific emphasis on evaluation of a) the of the larger craters and basins (e.g., Antoniadi), ex- regional effects of impact basin formation, and b) the hibit low albedo and smooth surfaces and may contain spatial distribution of ejecta, in particular resulting mare. Higher albedo deposits tend to contain a higher from formation of the South Pole-Aitken (SPA) basin density of superposed impact craters. and other large basins. Key scientific objectives in- Antoniadi Crater. Antoniadi crater (D=150 km; clude: 1) Determining the geologic history of LQ-30 69.5°S, 172°W) is unique for several reasons. First, and examining the spatial and temporal variability of Antoniadi is the only lunar crater that contains both a geologic processes within the map area. -

Ernst Zinner, Lithic Astronomer
UCLA UCLA Previously Published Works Title Ernst Zinner, lithic astronomer Permalink https://escholarship.org/uc/item/0gq43750 Journal Meteoritics & Planetary Science, 42(7/8) ISSN 1086-9379 Author Mckeegan, Kevin D. Publication Date 2007-07-01 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Meteoritics & Planetary Science 42, Nr 7/8, 1045–1054 (2007) Abstract available online at http://meteoritics.org Ernst Zinner, lithic astronomer Kevin D. MCKEEGAN Department of Earth and Space Sciences, University of California, Los Angeles, Los Angeles, California 90095–1567, USA E-mail: [email protected] It is a rare privilege to be one of the founders of an entirely new field of science, and it is especially remarkable when that new field belongs to the oldest branch of “natural philosophy.” The nature of the stars has perplexed and fascinated humanity for millennia. While the sources of their luminosity and their structures and evolution were revealed over the last century, it is thanks to the pioneering efforts of a rare and remarkable man, Ernst Zinner, as well as his colleagues and students (mostly at the University of Chicago and at Washington University in Saint Louis), that in the last two decades it has become possible to literally hold a piece of a star in one’s hand. Armed with sophisticated microscopes and mass spectrometers of various sorts, these “lithic astronomers” are able to reveal stellar processes in exquisite detail by examining the chemical, mineralogical, and especially the nuclear properties of these microscopic grains of stardust. With this special issue of Meteoritics & Planetary Science, we honor Ernst Zinner (Fig. -

Chandrayaan-2 Completes a Year Around the Moon
One-year completion of Chandrayaan-2 Lunar orbit insertion (August 20, 2019) Chandrayaan-2 completes a year around the Moon The Moon provides the best linkage to understand Earth’s early history and offers an undisturbed record of the inner Solar system environment. It could also be a base for future human space exploration of the solar system and a unique laboratory, unlike any on Earth, for fundamental physics investigations. In spite of several missions to the Moon, there remains several unanswered questions. Continued high resolution studies of its surface, sub-surface/interior and its low-density exosphere, are essential to address diversities in lunar surface composition and to trace back the origin and evolution of the Moon. The clear evidence from India’s first mission to the Moon, Chandrayaan-1, on the extensive presence of surface water and the indication for sub- surface polar water-ice deposits, argues for more focused studies on the extent of water on the surface, below the surface and in the tenuous lunar exosphere, to address the true origin and availability of water on Moon. With the goal of expanding the lunar scientific knowledge through detailed studies of topography, mineralogy, surface chemical composition, thermo-physical characteristics and the lunar exosphere, Chandrayaan-2 was launched on 22nd July 2019 and inserted into the lunar orbit on 20th August 2019, exactly one year ago. Though the soft-landing attempt was not successful, the orbiter, which was equipped with eight scientific instruments, was successfully placed in the lunar orbit. The orbiter completed more than 4400 orbits around the Moon and all the instruments are currently performing well. -

Glossary Glossary
Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts. -

General Disclaimer One Or More of the Following Statements May Affect
General Disclaimer One or more of the Following Statements may affect this Document This document has been reproduced from the best copy furnished by the organizational source. It is being released in the interest of making available as much information as possible. This document may contain data, which exceeds the sheet parameters. It was furnished in this condition by the organizational source and is the best copy available. This document may contain tone-on-tone or color graphs, charts and/or pictures, which have been reproduced in black and white. This document is paginated as submitted by the original source. Portions of this document are not fully legible due to the historical nature of some of the material. However, it is the best reproduction available from the original submission. Produced by the NASA Center for Aerospace Information (CASI) ^i e I !emote sousing sad eeolegio Studies of the llaistary Crusts Bernard Ray Hawke Prince-1 Investigator a EL r Z^ .99 University of Hawaii Hawaii Institute of Geophysics Planetary Geosciences Division Honolulu, Hawaii 96822 ^y 1i i W. December 1983 (NASA —CR-173215) REMOTE SENSING AND N84-17092 GEOLOGIC STUDIES OF THE PLANETARY CRUSTS Final Report ( Hawaii Inst. of Geophysics) 14 p HC A02/MF 101 CSCL 03B Unclas G3/91 11715 Gy -2- ©R1GNAL OF POOR QUALITY Table of Contents Page I. Remote Sensing and Geologic Studies cf Volcanic Deposits . • . 3 A. Spectral reflectance studies of dark-haloed craters. • . 3 B. Remote s^:sing studies of regions which were sites of ancient volcanisa . 3 C. [REEP basalt deposits in the Imbrium Region. -

Origins of Life: Transition from Geochemistry to Biogeochemistry
December 2016 Volume 12, Number 6 ISSN 1811-5209 Origins of Life: Transition from Geochemistry to Biogeochemistry NITA SAHAI and HUSSEIN KADDOUR, Guest Editors Transition from Geochemistry to Biogeochemistry Staging Life: Warm Seltzer Ocean Incubating Life: Prebiotic Sources Foundation Stones to Life Prebiotic Metal-Organic Catalysts Protometabolism and Early Protocells pub_elements_oct16_1300&icpms_Mise en page 1 13-Sep-16 3:39 PM Page 1 Reproducibility High Resolution igh spatial H Resolution High mass The New Generation Ion Microprobe for Path-breaking Advances in Geoscience U-Pb dating in 91500 zircon, RF-plasma O- source Addressing the growing demand for small scale, high resolution, in situ isotopic measurements at high precision and productivity, CAMECA introduces the IMS 1300-HR³, successor of the internationally acclaimed IMS 1280-HR, and KLEORA which is derived from the IMS 1300-HR³ and is fully optimized for advanced U-Th-Pb mineral dating. • New high brightness RF-plasma ion source greatly improving spatial resolution, reproducibility and throughput • New automated sample loading system with motorized sample height adjustment, significantly increasing analysis precision, ease-of-use and productivity • New UV-light microscope for enhanced optical image resolution (developed by University of Wisconsin, USA) ... and more! Visit www.cameca.com or email [email protected] to request IMS 1300-HR³ and KLEORA product brochures. Laser-Ablation ICP-MS ~ now with CAMECA ~ The Attom ES provides speed and sensitivity optimized for the most demanding LA-ICP-MS applications. Corr. Pb 207-206 - U (238) Recent advances in laser ablation technology have improved signal 2SE error per sample - Pb (206) Combined samples 0.076121 +/- 0.002345 - Pb (207) to background ratios and washout times. -

Science Concept 5: Lunar Volcanism Provides a Window Into the Thermal and Compositional Evolution of the Moon
Science Concept 5: Lunar Volcanism Provides a Window into the Thermal and Compositional Evolution of the Moon Science Concept 5: Lunar volcanism provides a window into the thermal and compositional evolution of the Moon Science Goals: a. Determine the origin and variability of lunar basalts. b. Determine the age of the youngest and oldest mare basalts. c. Determine the compositional range and extent of lunar pyroclastic deposits. d. Determine the flux of lunar volcanism and its evolution through space and time. INTRODUCTION Features of Lunar Volcanism The most prominent volcanic features on the lunar surface are the low albedo mare regions, which cover approximately 17% of the lunar surface (Fig. 5.1). Mare regions are generally considered to be made up of flood basalts, which are the product of highly voluminous basaltic volcanism. On the Moon, such flood basalts typically fill topographically-low impact basins up to 2000 m below the global mean elevation (Wilhelms, 1987). The mare regions are asymmetrically distributed on the lunar surface and cover about 33% of the nearside and only ~3% of the far-side (Wilhelms, 1987). Other volcanic surface features include pyroclastic deposits, domes, and rilles. These features occur on a much smaller scale than the mare flood basalts, but are no less important in understanding lunar volcanism and the internal evolution of the Moon. Table 5.1 outlines different types of volcanic features and their interpreted formational processes. TABLE 5.1 Lunar Volcanic Features Volcanic Feature Interpreted Process -

Hollenbach D CV2008.Pdf
SUMMARY CURRICULUM VITA DAVID JOHN HOLLENBACH Education: PhD., Theoretical Physics, Cornell University, 1969 Present Area of Research: Theoretical astrophysics, infrared astronomy, interstellar medium, star formation, astrochemistry, astrobiology Professional Activities: Senior member of American Astronomical Society, Senior member of International Astronomical Union, Study Scientist Large Deployable Telescope (LDR) Project (1980-84), Member of NASA Astronomy and Relativity Management Operation Working Group (ARMOWG) (1985-88), Scientific Organizing Committee for IAU Symposium 120, “Astrochemistry” (1984-85), Scientific Organizing Committee for Summer Schools on "Interstellar Processes”, The Interstellar Medium of Galaxies", and "The Evolution of Galaxies and Their Environment" (1985-1992), Director (PI) of the Center for Star Formation Studies, a consortium of NASA-Ames, UC Berkeley, and UC Santa Cruz Theoretical Astrophysicists funded by the NASA Theory Program (1985-2002), Member of the Executive Committee for the Space Sciences Laboratory, UC Berkeley (1985-1995), Co-Investigator on the Submillimeter Wave Astronomical Satellite (SWAS)(1988-present), Member of the Infrared Panel of the National Academy of Sciences Astronomy Astrophysics Survey Committee(1988-1990), Member of the ISO Short Wavelength Spectrometer Team (1990-2000), Member of the Stratospheric Observatory for Infrared Astronomy (SOFIA) Science Working Group (1990-1995), Member of the Submillimeter Science Working Group (1985-1995), Member of Executive Council of the American -
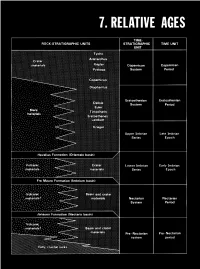
Relative Ages
CONTENTS Page Introduction ...................................................... 123 Stratigraphic nomenclature ........................................ 123 Superpositions ................................................... 125 Mare-crater relations .......................................... 125 Crater-crater relations .......................................... 127 Basin-crater relations .......................................... 127 Mapping conventions .......................................... 127 Crater dating .................................................... 129 General principles ............................................. 129 Size-frequency relations ........................................ 129 Morphology of large craters .................................... 129 Morphology of small craters, by Newell J. Fask .................. 131 D, method .................................................... 133 Summary ........................................................ 133 table 7.1). The first three of these sequences, which are older than INTRODUCTION the visible mare materials, are also dominated internally by the The goals of both terrestrial and lunar stratigraphy are to inte- deposits of basins. The fourth (youngest) sequence consists of mare grate geologic units into a stratigraphic column applicable over the and crater materials. This chapter explains the general methods of whole planet and to calibrate this column with absolute ages. The stratigraphic analysis that are employed in the next six chapters first step in reconstructing -

Landing Sites”
NationalNational Aeronautics Aeronautics and Space and Administration Space Administration SKGs, & ISECG “Landing Sites” Ben Bussey Chief Exploration Scientist Human Exploration & Operations Mission Directorate, NASA HQ 1 Strategic Knowledge Gaps • SKGs define information that is useful/mandatory for designing human spaceflight architecture • Perception is that SKGs HAVE to be closed before we can go to a destination, i.e. they represent Requirements • In reality, there is very little information that is a MUST HAVE before we go somewhere with humans. What SKGs do is buy down risk, allowing you to design simpler/cheaper systems. • There are three flavors of SKGs 1. Have to have – Requirements 2. Buys down risk – LM foot pads 3. Mission enhancing – Resources • Four sets of SKGs – Moon, Phobos & Deimos, Mars, NEOs www.nasa.gov/exploration/library/skg.html 2 Lunar Science-Exploration SKGs • Revisited and revised in 2016 • Architecture was unchanged, so SKG changes were based on new data since the previous SKG revision. • Effort led by LEAG. • Three Themes 1. Understand the lunar resource potential 2. Understand the lunar environment and its effect on human life 3. Understand how to work and live on the lunar surface 3 Findings • Recent missions produced data that was used to retire several of the SKGs defined by HAT and the 2011-2012 LEAG GAP-SAT analyses. • Thanks to these missions, there are no strategic knowledge gaps (SKG) that would inhibit the flight of any human mission (e.g., sortie or human-tended surface facility) <28 days duration. • However, there are several SKGs that should be addressed that would increase human safety not only at the Moon, but also in LEO, cislunar space, and beyond the Moon. -

Book of Abstracts
THE PHYSICS AND CHEMISTRY OF THE INTERSTELLAR MEDIUM Celebrating the first 40 years of Alexander Tielens' contribution to Science Book of Abstracts Palais des Papes - Avignon - France 2-6 September 2019 CONFERENCE PROGRAM Monday 2 September 2019 Time Speaker 10:00 Registration 13:00 Registration & Welcome Coffee 13:30 Welcome Speech C. Ceccarelli Opening Talks 13:40 PhD years H. Habing 13:55 Xander Tielens and his contributions to understanding the D. Hollenbach ISM The Dust Life Cycle 14:20 Review: The dust cycle in galaxies: from stardust to planets R. Waters and back 14:55 The properties of silicates in the interstellar medium S. Zeegers 15:10 3D map of the dust distribution towards the Orion-Eridanus S. Kh. Rezaei superbubble with Gaia DR2 15:25 Invited Talk: Understanding interstellar dust from polariza- F. Boulanger tion observations 15:50 Coffee break 16:20 Review: The life cycle of dust in galaxies M. Meixner 16:55 Dust grain size distribution across the disc of spiral galaxies M. Relano 17:10 Investigating interstellar dust in local group galaxies with G. Clayton new UV extinction curves 17:25 Invited Talk: The PROduction of Dust In GalaxIES C. Kemper (PRODIGIES) 17:50 Unravelling dust nucleation in astrophysical media using a L. Decin self-consistent, non steady-state, non-equilibrium polymer nucleation model for AGB stellar winds 19:00 Dining Cocktail Tuesday 3 September 2019 08:15 Registration PDRs 09:00 Review: The atomic to molecular hydrogen transition: a E. Roueff major step in the understanding of PDRs 09:35 Invited Talk: The Orion Bar: from ALMA images to new J. -

Physical Processes in the Interstellar Medium
Physical Processes in the Interstellar Medium Ralf S. Klessen and Simon C. O. Glover Abstract Interstellar space is filled with a dilute mixture of charged particles, atoms, molecules and dust grains, called the interstellar medium (ISM). Understand- ing its physical properties and dynamical behavior is of pivotal importance to many areas of astronomy and astrophysics. Galaxy formation and evolu- tion, the formation of stars, cosmic nucleosynthesis, the origin of large com- plex, prebiotic molecules and the abundance, structure and growth of dust grains which constitute the fundamental building blocks of planets, all these processes are intimately coupled to the physics of the interstellar medium. However, despite its importance, its structure and evolution is still not fully understood. Observations reveal that the interstellar medium is highly tur- bulent, consists of different chemical phases, and is characterized by complex structure on all resolvable spatial and temporal scales. Our current numerical and theoretical models describe it as a strongly coupled system that is far from equilibrium and where the different components are intricately linked to- gether by complex feedback loops. Describing the interstellar medium is truly a multi-scale and multi-physics problem. In these lecture notes we introduce the microphysics necessary to better understand the interstellar medium. We review the relations between large-scale and small-scale dynamics, we con- sider turbulence as one of the key drivers of galactic evolution, and we review the physical processes that lead to the formation of dense molecular clouds and that govern stellar birth in their interior. Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik, Albert-Ueberle-Straße 2, 69120 Heidelberg, Germany e-mail: [email protected], [email protected] 1 Contents Physical Processes in the Interstellar Medium ...............