DOCSLIB.ORG

Superconducting, Structural, and Magnetic Properties of Lithium and Lithium-Rich Compounds

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Superconducting, Structural, and Magnetic Properties of Lithium and Lithium-Rich Compounds SUPERCONDUCTING, STRUCTURAL, AND MAGNETIC PROPERTIES OF LITHIUM AND LITHIUM-RICH COMPOUNDS by Anne Marie Schaeffer Richards A dissertation submitted to the faculty of The University of Utah in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Physics Department of Physics and Astronomy The University of Utah May 2016 Copyright © Anne Marie Schaeffer Richards 2016 All Rights Reserved The University of Utah Graduate School STATEMENT OF DISSERTATION APPROVAL The dissertation of Anne Marie Schaeffer Richards has been approved by the following supervisory committee members: Stephan LeBohec Chair 11/24/2015 Date Approved Jordan Gerton Member 11/24/2015 Date Approved Eugene Mishchenko Member 11/24/2015 Date Approved Lowell Miyagi Member 11/24/2015 Date Approved Clayton Williams Member 11/24/2015 Date Approved and by Carleton DeTar Chair/Dean of the Department/College/School o f _____________Physics and Astronomy and by David B. Kieda, Dean of The Graduate School. ABSTRACT Lithium is generally considered to be a simple metal, given its simple electronic structure with one valence electron. It is considered to follow a nearly free electron model and have a nearly spherical Fermi surface. However, away from ambient conditions, the behavior of lithium becomes much less simple. Under high pressures, lithium undergoes a series of sym­ metry breaking phase transitions, even a metal to insulator transition; at low temperatures, lithium also undergoes a temperature-driven martensitic transformation. In this work, these deviations from simple models in lithium are investigated, both at ambient pressure and under high pressures, from the relative high temperature phenomenon of melting, to low temperature measurements of superconductivity. CONTENTS A B S T R A C T ................................................................................................................................ iii L IST O F F IG U R E S ................................................................................................................ vii L IST O F T A B L E S .................................................................................................................... xvi A C K N O W L E D G M E N T S .................................................................................................... xvii C H A P T E R S 1......I N T R O D U C T I O N ........................................................................................................... 1 1 .1 Alkali M etals.................................................................................................................. 1 1.2 L ithium ........................................................................................................................... 2 1.3 Quantum Solids.............................................................................................................. 2 1.3.1 Nearly Free Electron M o d e l............................................................................. 3 1.4 Extreme Conditions....................................................................................................... 4 1.4.1 Pressure.................................................................................................................. 4 1.4.2 Tem perature......................................................................................................... 5 1.5 High Pressure M elting.................................................................................................. 5 1.5.1 Quantum M eltin g............................................................................................... 7 1.6 Superconductivity......................................................................................................... 8 1.7 Crystal Structure........................................................................................................... 10 1.8 Fermi Surface ................................................................................................................ 14 2. E X P E R IM E N T A L T E C H N I Q U E S ........................................................................ 18 2.1 Pressure ............................................................................................................................ 18 2 .1 .1 Diamond Anvil Cell ........................................................................................... 18 2.1.2 Paris-Edinburgh Press......................................................................................... 21 2.1.3 Pressure Measurement ...................................................................................... 22 2.1.3.1 Ruby Fluorescence .................................................................................... 22 2.1.3.2 Equation of State ...................................................................................... 26 2.2 Temperature .................................................................................................................. 27 2.2.1 Low Temperature ................................................................................................ 27 2.2.1.1 Cryostat ....................................................................................................... 27 2.2.2 High Temperature ................................................................................................ 28 2.2.2.1 Laser H eating............................................................................................. 29 2.2.2.2 Resistive H ea tin g ...................................................................................... 29 2.3 High Pressure Resistance Measurements................................................................. 30 2.3.1 Resistance for Detecting Melting of Metals ................................................. 36 2.3.2 Resistance for Detecting Superconductivity................................................. 38 2.4 AC Magnetic Susceptibility ......................................................................................... 40 2.5 de Haas van Alphen Effect ........................................................................................ ...45 2.5.1 Torque Magnetometry........................................................................................ ...45 2.6 Diffraction..........................................................................................................................46 2.6.1 X-Ray D iffraction...................................................................................................46 2.6.2 Neutron Diffraction............................................................................................. ...50 2.6.3 Analysis.................................................................................................................. ...51 3. H IG H P R E S S U R E M E L T IN G O F L I T H I U M ....................................................54 3.1 Abstract ......................................................................................................................... ...54 3.2 Introduction .................................................................................................................. ...55 3.3 Methods ......................................................................................................................... ...56 3.4 Experim ent.................................................................................................................... ...59 3.5 Results .................................................................................................................................61 3.6 Conclusion ..........................................................................................................................63 3.7 Notes on Laser H eating............................................................................................... ...63 4. TWIN SAMPLE CHAMBER FOR SIMULTANEOUS ELECTRONIC TRANSPORT MEASUREMENT IN A DIAMOND ANVIL CELL ... 65 4.1 Abstract ......................................................................................................................... ...65 4.2 Introduction .................................................................................................................. ...6 6 4.3 Experimental Setup ..........................................................................................................67 4.4 Conclusion ..........................................................................................................................71 4.5 Notes ................................................................................................................................ ...72 5. HIGH-PRESSURE SUPERCONDUCTING PHASE DIAGRAM OF 6 LI: IS O T O P E E F F E C T S IN D E N S E L IT H IU M .............................................73 5.1 Abstract ......................................................................................................................... ...73 5.2 Introduction .................................................................................................................. ...74 5.3 Experiment and Results ............................................................................................. ...75 5.4 D iscussion..........................................................................................................................81 5.5 Notes on Pressure Distribution.....................................................................................84 6 . NEW BOUNDARIES FOR MARTENSITIC
Load more

Recommended publications
  • 14Th International Ceramics Congress June 4-8/2018 Forum on New Materials June 10-14/2018
    Astract Deadline • October 15, 2017 Perugia - Italy • June 4-14/2018 14th International Ceramics Congress June 4-8/2018 8th Forum on New Materials June 10-14/2018 www.cimtec-congress.org Benedetto Bonfigli, Porta Marzia in Perugia, XV sec. Invitation to Attend! CIMTEC 2018 - 14th International Conference on Modern Materials and Technologies - will be held in Peru- gia, Italy, June 4 to 14, 2018. CIMTEC 2018 will consist of the 14th International Ceramics Congress (June 4-8) and of the 8th Forum on New Materials (June 10-14), each of them including a number of Symposia, Special Sessions, and Conferences. As a major longstanding event for the international materials community, CIMTEC will again gather together a large and qualified audience of materials scientists, physicists, chemists and engineers and of experts of a wide range of the most demanding application areas of modern materials, from the molecular and nanoscales to large complex integrated systems. The National Research Council of Italy (CNR), the Italian National Agency for New Technology, Energy and the Environment (ENEA) will act as major endorsers of CIMTEC 2018 together with the World Academy of Ceramics (WAC), The International Ceramic Federation (ICF) and the International Union of the Materials Research Societies (IUMRS). The Chair, Co-Chairs and CIMTEC 2018 Committees invite you to foster the progress in the field by contrib- uting with your expertise to what promises to be a very comprehensive and exciting meeting, and to enjoy the immense unique artistic heritage and wonderful landscape of Umbria district. Pietro Vincenzini Co-Chairs CIMTEC 2018 General Chair CIMTEC Conferences Gary Messing National Research Council, Italy Penn State University, USA World Academy of Ceramics Takashi Goto Tohoku University, Japan International Ceramic Federation Robert P.H.
    [Show full text]
  • Underpinning of Soviet Industrial Paradigms
    Science and Social Policy: Underpinning of Soviet Industrial Paradigms by Chokan Laumulin Supervised by Professor Peter Nolan Centre of Development Studies Department of Politics and International Studies Darwin College This dissertation is submitted for the degree of Doctor of Philosophy May 2019 Preface This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration except as declared in the Preface and specified in the text. It is not substantially the same as any that I have submitted, or, is being concurrently submitted for a degree or diploma or other qualification at the University of Cambridge or any other University or similar institution except as declared in the Preface and specified in the text. I further state that no substantial part of my dissertation has already been submitted, or, is being concurrently submitted for any such degree, diploma or other qualification at the University of Cambridge or any other University or similar institution except as declared in the Preface and specified in the text It does not exceed the prescribed word limit for the relevant Degree Committee. 2 Chokan Laumulin, Darwin College, Centre of Development Studies A PhD thesis Science and Social Policy: Underpinning of Soviet Industrial Development Paradigms Supervised by Professor Peter Nolan. Abstract. Soviet policy-makers, in order to aid and abet industrialisation, seem to have chosen science as an agent for development. Soviet science, mainly through the Academy of Sciences of the USSR, was driving the Soviet industrial development and a key element of the preparation of human capital through social programmes and politechnisation of the society.
    [Show full text]
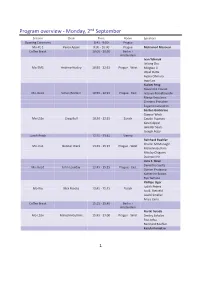
  • Program Overview ‐ Monday, 2ⁿd September
    Program overview ‐ Monday, 2ⁿd September Session Chair Time Room Speakers Opening Ceremony 8:45 ‐ 9:00 Prague Mo‐PL 1 Karen Appel 9:00 ‐ 10:00 Prague Mohamed Mezouar Coffee Break 10:00 ‐ 10:30 Berlin + Amsterdam Ivan Yahniuk Jinlong Zhu Mo‐EM1 Andrew Huxley 10:30 ‐ 12:15 Prague ‐ West Mingtao Li Utpal Dutta Ayako Ohmura Ingo Loa Xialoei Feng Alexandre Courac Mo‐Geo1 Simon Redfern 10:30 ‐ 12:15 Prague ‐ East Tetsuya Komabayashi Marija Krstulovic Clemens Prescher Eugenio Calandrini Gaston Garbarino Gunnar Weck Mo‐LS1x Craig Bull 10:30 ‐ 12:15 Zürich Catalin Popescu Karen Appel Jennifer Sears Joseph Boby Lunch Break 12:15 ‐ 13:45 Vienna Reinhard Boehler Charlie McMonagle Mo‐Ins1 Gunnar Weck 13:45 ‐ 15:15 Prague ‐ West Malcolm Guthrie Nikolay Chigarev Duanwei He Livia E. Bove Demetrio Scelta Mo‐Geo2 John Loveday 13:45 ‐ 15:15 Prague ‐ East Ciprian Pruteanu Katherine Brown Ryo Yamane Phillipe Oger Judith Peters Mo‐Bio Nick Brooks 13:45 ‐ 15:15 Zürich Ivo B. Rietveld László Smeller Anais Cario Coffee Break 15:15 ‐ 15:45 Berlin + Amsterdam Noriki Terada Mo‐LS2n Malcolm Guthrie 15:45 ‐ 17:00 Prague ‐ West Dmitry Sokolov Pau Jorba Reinhard Boehler Kazuki Komatsu 1 Program overview ‐ Monday, 2ⁿd September Mo‐Geo3 Livia E. Bove 15:45 ‐ 17:00 Prague ‐ East Samuele Fanetti Dane Sterbentz Sooheyong Lee Kateřina Štulíková Mo‐Food Jorge Saraiva 15:45 ‐ 17:00 Zürich Concepción P. Lamela Izabela Porębska Milan Houška Poster Session 1 17:00 ‐ 18:45 Berlin 8:45 ‐ 9:00 Opening Ceremony Room Prague 9:00 ‐ 10:00 Plenary Lecture 1 Room Prague Chair Karen Appel
    [Show full text]
  • 55 Th EHPRG Guide.Pdf
    www.ehprg2017.org 55th European High Pressure Research Group Meeting: High Pressure Science and Technology PROGRAMME 1 55th EHPRG Poznań, 3-8 September 2017 Programme Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Programme Overview Time schedule Time schedule 3 September 2017 4 September 2017 5 September 2017 6 September 2017 7 September 2017 8 September 2017 8.00-8.30 Registration 8.00-8.30 Registration Registration Special Session: Morasko Registration 8.30-9.00 Opening Ceremony 8.45 8.30-9.00 Meteorite Reserve 9.00-9.30 PL2 - Natalia 9.00-9.30 PL1 - Ho-Kwang Mao PL3 - Chris Michiels Mirosław Makohonienko PL5 - Przemysław Dera Dubrovinskaia Room 2.64 Room 2.64 Start in Room 2.64 Room 2.64 9.30-10.00 Room 2.64 9.30-10.00 10.00-10.30 Coffee Break Coffee Break Coffee Break Coffee Break Coffee Break 10.00-10.30 10.30-11.00 S 1 S 2 S 3 S 6 S 9 S 10 S 11 S 12 S 17 S 18 S 20 S 22 S 23 S 24 S 26 S 27 S 28 10.30-11.00 11.00-11.30 2.64 2.61 3.65 2.62 2.62 2.61 3.65 2.64 3.65 2.62 2.64 2.62 3.65 2.64 2.62 3.65 2.64 11.00-11.30 11.30-12.00 11.30-12.00 12.00-12.30 12.00-12.30 12.30-13.00 Lunch Break/Special Closing Ceremony 12.40 12.30-13.00 Lunch Break EHPRG General Session: “Women Under 13.00-13.30 Lunch Break Assembly 13.00-13.30 Pressure gathering” Room 2.64 Lunch 13.30-14.00 EHPRG Group Photo Room 2.57 13.30-14.00 14.00-14.30 S 5 S 4 S 7 S 8 S 13 S 14 S 15 S 16 PL4 - Elena Boldyreva 14.00-14.30 Lunch Break 14.30-15.00 2.64 2.61 3.65 2.62 3.65 2.61 2.64 2.62 Room 2.64 14.30-15.00 15.00-15.30 15.00-15.30 15.30-16.00 Poster Session 2 15.30-16.00
    [Show full text]
  • Pushing Towards Room-Temperature Superconductivity
    VIEWPOINT Pushing Towards Room-Temperature Superconductivity Two independent studies report superconductivity at record high temperatures in hydrogen-rich materials under extreme pressure. by Eva Zurek∗ groups, the first led by Russell Hemley at the George Wash- ington University in Washington, DC [2], and the second by uperconductivity, the ability of a material to conduct Mikhail Eremets at the Max Planck Institute for Chemistry, electricity without any resistance, was first observed Germany [3], have now reported experiments indicating that in 1911 in solid mercury below a critical temperature a hydride of lanthanum compressed to 170–185 GPa has a Tc (Tc) of 4.2 K. Ever since, countless scientists have been of 250–260 K [2, 3]. The results bode well for the search for Ssearching for a material whose Tc exceeds room tempera- room-temperature superconductors—the reported materials ture. For a long time this holy grail seemed unattainable—a could already work without the need for cooling on an aver- linear extrapolation of research progress from 1911 to 1970 age winter night in the Arctic! suggested that Tc would reach room temperature around In 1968, physicist Neil Ashcroft predicted that metallic the year 2840! The discovery of high-temperature super- hydrogen should have all of the properties required to be conductivity in copper oxides raised Tc above liquid helium a high-temperature superconductor according to Bardeen- temperature. Since 1994, one of the copper oxides has held Cooper-Schrieffer (BCS) theory [4]. Unfortunately, metalliz- the record for the highest Tc (133 K at atmospheric pressure ing hydrogen in static compression experiments turned out and 164 K under high pressure).
    [Show full text]
  • 8705K CIW 2002 YB Text
    THE PRESIDENT’ S REPORT Year Book 01/02 July 1, — June 30, CARNEGIE INSTITUTION OF WASHINGTON Department of Embryology ABOUT CARNEGIE 115 West University Parkway Baltimore, MD 21210-3301 410.554.1200 . TO ENCOURAGE, IN THE BROADEST AND Department of Plant Biology MOST LIBERAL MANNER, INVESTIGATION, 260 Panama St. RESEARCH, AND DISCOVERY, AND THE Stanford, CA 94305-4101 650.325.1521 APPLICATION OF KNOWLEDGE TO THE Geophysical Laboratory IMPROVEMENT OF MANKIND . 5251 Broad Branch Rd., N.W. Washington, DC 20015-1305 202.478.8900 The Carnegie Institution of Washington Department of Terrestrial Magnetism was incorporated with these words in 1902 5241 Broad Branch Rd., N.W. Washington, DC 20015-1305 by its founder, Andrew Carnegie. Since 202.478.8820 then, the institution has remained true to The Carnegie Observatories 813 Santa Barbara St. its mission. At six research departments Pasadena, CA 91101-1292 across the country, the scientific staff and 626.577.1122 a constantly changing roster of students, Las Campanas Observatory Casilla 601 postdoctoral fellows, and visiting investiga- La Serena, Chile tors tackle fundamental questions on the Department of Global Ecology 260 Panama St. frontiers of biology, earth sciences, and Stanford, CA 94305-4101 astronomy. 650.325.1521 Office of Administration 1530 P St., N.W. Washington, DC 20005-1910 202.387.6400 http://www.CarnegieInstitution.org ISSN 0069-066X Design by Hasten Design, Washington, DC Printing by Mount Vernon Printing, Landover, MD March 2003 CONTENTS The President’s Commentary Losses, Gains, Honors Contributions, Grants, and Private Gifts First Light and CASE Geophysical Laboratory Department of Plant Biology Department of Embryology The Observatories Department of Terrestrial Magnetism Department of Global Ecology Extradepartmental and Administrative Financial Statements An electronic version of the Year Book is accessible via the Internet at www.CarnegieInstitution.org/yearbook.html.
    [Show full text]
  • Superstripes 2017
    SUPERSTRIPES 2017 edited by Antonio Bianconi superstripes press S u p e r s t r i p e s P r e ss science series SUPERSTRIPES 2017 Quantum in Complex Matter: Superconductivity, Magnetism & Ferroelectricity edited by Antonio Bianconi superstripes press S u p e r s t r i p e s P r e ss science series Science Series No.11 Title: Superstripes 2017 Published on June 2017 by Superstripes Press, Rome, Italy http://www.superstripes.net/science/science.htm © 2017 Superstripes Press © 2017 Multiple authors ISBN 978-88-6683-069-6 ISBN-A 10.978.886683/0696 This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA. Authors : Abbamonte P., Aeppli G., Alarco J.A., Albertini R., Aoki D., Attanasio C., Avigo I., Babaev E., Bachar N., Badoux S., Balakirev F.F., Balicas L., Bao W., Barbiellini B., Berciu M., Berthod C., Bianconi A., Billinge S.J.L., Bonca J., Boris A., Borisenko S., Borzenets I., Bozin E.S., Brazovskii S., Brun C., Bussmann-Holder A., Capone M., Carlström J., Chang J., Chávez I., Chu P.C.W., Conradson S.D., Coslovich G., Crisan A., Daghero D., de Llano M., de’ Medici L., Dean M. P. M., Degiorgi L., Destraz D., Deutscher G., Di Gioacchino M., Di Giorgio C., Dobrosavljevic V., Drechsler S.L., Efremov D., Egami T., Einaga M., Eremets M.I., Eremin I., Eremin M., Fanfarillo L., Farina D., Feng S., Fine B.V., Fink J., Flammia L., Frésard R.,
    [Show full text]
  • Appendices to Agenda 1 25 GA
    Appendices to Agenda 1 25 GA INTERNATIONAL UNION OF CRYSTALLOGRAPHY TWENTY-FIFTH GENERAL ASSEMBLY Appendix 1 to Agenda Approval of Agenda By-Law 1.7 requires that, unless decided otherwise by the General Assembly, matters concerning adherence to the Union shall take precedence over all other business at the first business session of the General Assembly. Appendix 2 to Agenda Amendments to Statutes and By-Laws affecting adherence to the Union There are no proposals to amend the Statutes and By-Laws in matters affecting adherence to the Union. Appendix 3 to Agenda Applications for membership of the Union United Arab Emirates An application for membership has been received from the President of the Emirates Crystallographic Society for membership of United Arab Emirates in Category I. The Adhering Body would be the Emirates Crystallographic Society (ECS), UAE, which undertakes to pay the subscription. The National Committee for Crystallography would comprise the Executive Committee and Commission Chairs of the ECS: P. Naumov (Chair), S. Mohamed (Vice-Chair), L. Li (Secretary), W. Rabeh, B.M. Suleiman, K. Daoudi, M.T.A. Khaleel, D. Anjum, S. Kaliappan. At the time of preparing these papers there are 15 entries in the World Database of Crystallographers for UAE. The Executive Committee has considered the application and recommends to the General Assembly that the application be approved. Guatemala An application for membership has been received from the President of the Guatemalan Crystallographic Association (ACriGUA), for membership of Guatemala in Category I. The Adhering Body would be the National Secretariat of Science and Technology, Senacyt-Guatemala, which undertakes to pay the subscription.
    [Show full text]
  • Elemental Metamorphosis
    PHYSICS & ASTRONOMY_High-Pressure Research Elemental Metamorphosis The inside of planets, stellar shells and numerous other uncomfortable spots in space have one thing in common: matter there is under extreme pressure of several million atmospheres. Mikhail Eremets and his colleagues produce such cosmic pressures in their lab at the Max Planck Institute for Chemistry in Mainz – and they do so in surprisingly simple experiments. They are researching which unique transformations gases, but also metals, undergo under these conditions. TEXT ROLAND WENGENMAYR he cosmos is full of places Since this world-record-setting mea- where the extreme is nor- surement, many chemists, materials mal. “In the core of Jupiter, scientists and physicists are contem- for example, the pressure is plating new, fascinating questions: more than 30 million atmo- Does hydrogen even become super- T spheres,” explains Mikhail Eremets at conducting at room temperature at the Max Planck Institute for Chemistry even higher pressure – in other words, Ich weiß nicht genau, was zusammengehört, in Mainz: “And planetary researchers does it conduct electricity entirely have long suspected that hydrogen, without electrical resistance? That is which is the primary component of precisely what theoreticians predict. these gas planets, is metallic there.” Only residents of Jupiter – if there American physicists Eugene Wigner were any – would be able to use super- and Hillard Bell Huntington predicted conductive extreme-pressure hydro- this strange, solid state of hydrogen as gen in electrical cables. However, the far back as 1935. Until recently, though, discovery of room-temperature super- it remained just speculation. It wasn’t conductivity in hydrogen could help until 2011 that the small Max Planck in solving the mystery of high-tem- team led by Mikhail Eremets, a Russian, perature superconductors and in tai- provided certainty with its experiments.
    [Show full text]
  • COMMISSION STAFF WORKING DOCUMENT INTERIM EVALUATION of HORIZON 2020 ANNEX 2
    Council of the European Union Brussels, 31 May 2017 (OR. en) 9787/17 ADD 7 RECH 211 COMPET 454 IND 142 MI 458 EDUC 272 TELECOM 148 ENER 255 ENV 551 REGIO 65 AGRI 289 TRANS 227 SAN 224 COVER NOTE From: Secretary-General of the European Commission, signed by Mr Jordi AYET PUIGARNAU, Director date of receipt: 29 May 2017 To: Mr Jeppe TRANHOLM-MIKKELSEN, Secretary-General of the Council of the European Union No. Cion doc.: SWD(2017) 221 final - PART 8/16 Subject: COMMISSION STAFF WORKING DOCUMENT INTERIM EVALUATION of HORIZON 2020 ANNEX 2 Delegations will find attached document SWD(2017) 221 final - PART 8/16. Encl.: SWD(2017) 221 final - PART 8/16 9787/17 ADD 7 SD/MI/lv DG G 3 C EN EUROPEAN COMMISSION Brussels, 29.5.2017 SWD(2017) 221 final PART 8/16 COMMISSION STAFF WORKING DOCUMENT INTERIM EVALUATION of HORIZON 2020 ANNEX 2 {SWD(2017) 220 final} {SWD(2017) 222 final} EN EN A. EUROPEAN RESEARCH COUNCIL A.1. INTRODUCTION A.1.1. Context In 2000 Commissioner Philippe Busquin announced the European Research Area (ERA), and in March, the Lisbon Strategy was adopted. This started a period of reflection among the European scientific and policymaking communities on how best to support research and innovation (R&I) at the EU level1. Since its inception the EU framework programmes had supported transnational collaboration “on predetermined topics and subjects in applied, finalised or directed research fields, corresponding to the Union’s major policies in the fields of health, energy, the environment, etc.”2 The emerging debate emphasised instead the central importance of basic research to the relative performance of the innovation systems of the US and Europe.
    [Show full text]
  • Arxiv:1907.11916V1 [Cond-Mat.Supr-Con] 27 Jul 2019 Have Been Predicted to Be Thermodynamically Stable at Estimated to Be Between 9 and 12
    Quantum Crystal Structure in the 250 K Superconducting Lanthanum Hydride Ion Errea,1, 2, 3 Francesco Belli,1, 2 Lorenzo Monacelli,4 Antonio Sanna,5 Takashi Koretsune,6 Terumasa Tadano,7 Raffaello Bianco,2 Matteo Calandra,8 Ryotaro Arita,9, 10 Francesco Mauri,4, 11 and José A. Flores-Livas4 1Fisika Aplikatua 1 Saila, Gipuzkoako Ingeniaritza Eskola, University of the Basque Country (UPV/EHU), Europa Plaza 1, 20018 Donostia/San Sebastián, Spain 2Centro de Física de Materiales (CSIC-UPV/EHU), Manuel de Lardizabal Pasealekua 5, 20018 Donostia/San Sebastián, Spain 3Donostia International Physics Center (DIPC), Manuel de Lardizabal Pasealekua 4, 20018 Donostia/San Sebastián, Spain 4Dipartimento di Fisica, Università di Roma La Sapienza, Piazzale Aldo Moro 5, I-00185 Roma, Italy 5Max-Planck Institute of Microstructure Physics, Weinberg 2, 06120 Halle, Germany 6Department of Physics, Tohoku University, 6-3 Aza-Aoba, Sendai, 980-8578 Japan 7Research Center for Magnetic and Spintronic Materials, National Institute for Materials Science, Tsukuba 305-0047, Japan 8Sorbonne Université, CNRS, Institut des Nanosciences de Paris, UMR7588, F-75252, Paris, France 9Department of Applied Physics, University of Tokyo, 7-3-1 Hongo Bunkyo-ku, Tokyo 113-8656 Japan 10RIKEN Center for Emergent Matter Science, 2-1 Hirosawa, Wako, 351-0198, Japan 11Graphene Labs, Fondazione Istituto Italiano di Tecnologia, Via Morego, I-16163 Genova, Italy (Dated: July 30, 2019) The discovery of superconductivity at 200 K in the hydrogen sulfide system at large pressures [1] was a clear demonstration that hydrogen-rich materials can be high-temperature superconductors. The recent synthesis of LaH10 with a superconducting critical temperature (Tc) of 250 K [2, 3] places these materials at the verge of reaching the long-dreamed room-temperature superconductivity.
    [Show full text]
  • Structural Transitions in Solids: Theory, Simulations, Experiments and Visualization Techniques
    Structural Transitions in Solids: Theory, Simulations, Experiments and Visualization Techniques CECAM-USI-LUGANO 8-11 July 2009 Stefano LEONI Max-Planck Institute CPfS, Dresden, Germany Roman MARTOŇÁK Comenius University, Bratislava, Slovakia Michele PARRINELLO ETHZ, USI Campus, Lugano, Switzerland Jean FAVRE Swiss Supercomputing Centre (CSCS), Manno, Switzerland 1 2 3 4 “Research on novel materials is nowadays among the fastest growing fields of scientific activity, with a tremendous technological and social impact. The quest for novel materials with critical properties has boosted the developments of novel techniques to improve material fabrication. At the same time, the increasing need of a rational approach to material sciences has promoted an extensive effort on the theoretical and numerical side. The contribution and impact of theory and simulations in this field has recently grown to such an extent, that not only a reliable and firm framework can be provided, due to a large number of novel numerical methods and simulation approaches. More importantly, numerical simulations can perform truly predictively by now. This fact has opened completely new scenarios for a novel way of interaction between simulation and practice, beyond the historical dichotomy theory-experiment. Theory can not only justify experimental results, but can take on the task of guiding experiments in difficult situations, on unknown grounds. The identification of stable and metastable phases, the elucidation of reaction and transformation mechanisms, the precise and complete
    [Show full text]