DOCSLIB.ORG

Superstripes 2017

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Superstripes 2017 SUPERSTRIPES 2017 edited by Antonio Bianconi superstripes press S u p e r s t r i p e s P r e ss science series SUPERSTRIPES 2017 Quantum in Complex Matter: Superconductivity, Magnetism & Ferroelectricity edited by Antonio Bianconi superstripes press S u p e r s t r i p e s P r e ss science series Science Series No.11 Title: Superstripes 2017 Published on June 2017 by Superstripes Press, Rome, Italy http://www.superstripes.net/science/science.htm © 2017 Superstripes Press © 2017 Multiple authors ISBN 978-88-6683-069-6 ISBN-A 10.978.886683/0696 This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA. Authors : Abbamonte P., Aeppli G., Alarco J.A., Albertini R., Aoki D., Attanasio C., Avigo I., Babaev E., Bachar N., Badoux S., Balakirev F.F., Balicas L., Bao W., Barbiellini B., Berciu M., Berthod C., Bianconi A., Billinge S.J.L., Bonca J., Boris A., Borisenko S., Borzenets I., Bozin E.S., Brazovskii S., Brun C., Bussmann-Holder A., Capone M., Carlström J., Chang J., Chávez I., Chu P.C.W., Conradson S.D., Coslovich G., Crisan A., Daghero D., de Llano M., de’ Medici L., Dean M. P. M., Degiorgi L., Destraz D., Deutscher G., Di Gioacchino M., Di Giorgio C., Dobrosavljevic V., Drechsler S.L., Efremov D., Egami T., Einaga M., Eremets M.I., Eremin I., Eremin M., Fanfarillo L., Farina D., Feng S., Fine B.V., Fink J., Flammia L., Frésard R., Fujimori A., Fujita M., Galda A., Giannetti C., Glatz A., Goncharov A.F., Goto H., Goto Y., Gray A.X., Grilli M., Grochala W., Guguchia Z., Guidi T., Guo H., Guzman-Verri G.G., Hanaguri T., Hayden S., Hess C., Huecker M., Iavarone M., Ideue T., Imada M., Irizawa A., Ivanov A.A., Jackeli G., Joon E., Jurkutat M., Kanazawa I., Kapcia K.J., Kataev V., Kato R., Khaliullin G., Khomski D.I., Kimura A., Kimura T., Kirova N., Knebel G., Kokalj J., Kolodziej J.J., Komarek A.C., Kontani H., Kresin V., Kruger F., Krzton-Maziopa A., Ksenofontov V., Kubozono Y., Langerome B., Larkin T.I., Leridon B., Littlewood P., Liu C., Lorenzana J., Louca D., Luo J., Lychkovskiy O., Madan I., Maeno Y., Marcelli A., Markiewicz R.S., Marsiglio F., Massarotti D., Mazziotti M.V., Mazzoli C., McNally D.E., Mertelj T., Mesaros A., Miletto Granozio F., Mironov A. Yu., Miyasaka S., Mizuguchi Y., Mizukami Y., Moewes A., Momono N., Monney C., Moreo A., Moroni M., Moskvin A.S., Mukhin S.I., Mustre de León J., Nattermann T., Neilson D., Nissinen J., Oda M., Oles A.M., Orgad D., Orth P.P., Ovchinnikov S.G., Pelliciari J., Peng Y., Perali A., Perring T., Pomarico E., Ponomarenko L.A., Popović D., Prassides K., Ptok A., Pudalov V., Purans J., Puzniak R., Quader K., Raimondi R., Rajasekaran S., Renner Ch., Reznik D., Robinson I.K., Roy P., Sanna S., Sato M., Schmitt T., Schneider W.-D., Seibold G., Semenov A.G., Shen D., Shengelaya A., Shi M., Shimizu K., Shimojima T., Silaev M., Silhanek A.V., Soh Y.-Ah, Soldatov A.V., Spera M., Spivak B., Steppke A., Stornaiuolo D., Strinati Calvanese G., Sumida K., Sunko V., Sushkov O.P., Tafuri F., Tallon J., Tanatar B., Tanner D.B., Teitel’baum G., Terao T., Timusk T., Toda Y., Tortello M., Tripathi V., Truccato M., Tsuchiizu M., Uemura Y.J., van der Marel D., van Wezel J., Vanacore G.M., Vargas-Paredes A.A., Vinokur V.M., von Rohr F., Wahl P., Wall S., Wirth S., Wohlfeld K., Wysokiński K.I., Wysokinski M.M., Yanagisawa T., Yoshida Y., Zaanen J., Zaikin A.D., Zhigadlo N.D., Zhuang J., Zwicknagl G. *These authors presented the scientific reports collected in this book at the Superstripes 2017 conference held in Ischia (It) on June 4-10, 2017 Papers presented at the international conference Superstripes 2017 Ischia Italy June 4-10, 2017 Organized by Non profit organization for scientific research Superstripes onlus Rome International Center for Materials Science Superstripes - RICMASS Chairman Prof. Antonio Bianconi, RICMASS, Rome, I Organizing Committee Gabriel Aeppli, Paul Scherrer Institute, CH Bernd Büchner, IFW Dresden, D Takeshi Egami, University of Tennessee, USA Vladimir Kresin, University of California, USA P.B. Littlewood, Argonne National Laboratory, UK Despina Louca, University of Virginia, Charlottesville, USA Andrea Perali, University of Camerino, I Kosmas Prassides, Durham University, UK Valerii Vinokur, Argonne National Laboratory, USA Jan Zaanen, University of Leiden, NL Superstripes 2017, Ischia June 410, 2017 Superstripes 2017 Book of Abstracts Superstripes 2017, Ischia June 410, 2017 Table of Contents Guy Deutscher: Multi-level Kondo effect and enhanced critical temperature in nanoscale granular Al............................................................................................ 12 Steven Conradson: The Fröhlich-type, nonequilibrium, polaronic condensate in the Mott system UO2(+x) ........................................................................................... 13 Leonardo Degiorgi: Investigation of the optical anisotropy in the nematic phase of FeSe ..................................................................................................................... 14 Kosmas Prassides: New candidate quantum spin liquids in ionic polyaromatic hydrocarbons ........................................................................................................ 16 Dmitry Reznik: Dynamic charge stripe spectrum in nickelate perovskites .............. 17 Yoshiteru Maeno: Mott transition and strong diamagnetism in Ca2RuO4 tuned by electric field/current .............................................................................................. 18 Annette BussmannHolder: The road map toward room temperature superconductivity .................................................................................................. 20 9 Takeshi Egami: d Nickelates under Pressure ........................................................ 22 Yasutomo Uemura: Three novel features in the correlations between Tc and the superfluid density: local phase coherence below the Bose gas temperature TB and multiple ratios of Tc/TF .......................................................................................... 24 Vladimir Kresin: Electron-lattice and electronelectron interactions in novel systems: paths to room temperature superconductivity......................................................... 27 Hiroshi Kontani: Strong interplay between high-Tc superconductivity, nematicity, and magnetism in Fe-based Superconductors......................................................... 28 Daniel Khomskii: Strong covalency and ligand holes, or how to make magnetic gold?..................................................................................................................... 29 Stephen Hayden: Spin and charge-density-wave fluctuations in cuprates ............... 30 Johan Chang: Electronics of high-temperature cuprate superconductors ................ 32 Naoki Momono: 1/8 Anomaly and Charge Order in Dydoped Bi2212 .................. 33 Masaki Fujita: Neutron-Scattering Study of Magnetic Excitations in Electron-Doped Cuprate ................................................................................................................. 35 Dirk van der Marel: Superconductivity and electronic structure of SrTiO3 ............ 37 Yoshihiro Kubozono: Pressure-driven highTc superconductivity in carbon-based and inorganic materials ......................................................................................... 39 Akio Kimura: Non-equilibrium Surface Dirac Fermion Dynamics of Topological Insulators Probed By Time Resolved ARPES ........................................................ 41 Dragana Popović: Charge dynamics near the onset of charge-density-wave order in La-214 cuprates .................................................................................................... 43 Dror Orgad: Dimensional Crossover of Charge-Density Wave Correlations in the Cuprates ............................................................................................................... 45 Superstripes 2017, Ischia June 410, 2017 Marco Truccato: Modifications induced by synchrotron radiation in Bi2Sr2CaCu2O8+delta and YBa2Cu3O7x: a novel non-destructive patterning method .................................................................................................................. 46 Michael Jurkutat: Local charges and charge order in the cuprates revealed by NMR ............................................................................................................................. 48 Nikolai Zhigadlo: Crystal Growth and Advanced Synthesis of Contemporary Functional and Superconducting Materials: From Simplicity to Complexity .......... 49 Alexander Shengelaia: Rapid Synthesis of Superconducting and Magnetic oxides by Light Irradiation .................................................................................................... 51 Jose Alarco: A complete and accurate description of superconductivity of AlB2 – type structures from phonon dispersion calculations .............................................. 52 Wolf-Dieter Schneider: Atomic structure of supported ultrathin Germania films.... 54 Mauro Tortello: Nanoscale Characterization of the Thermal Conductivity of Supported Graphite Nanoplates, Graphene and Few-layer Graphene ..................... 55 Yoshikazu Mizuguchi: Material design strategies for BiCh2based layered superconductors ...................................................................................................
Load more

Recommended publications
  • Arxiv:1701.03127V1 [Cond-Mat.Supr-Con] 11 Jan 2017 Scnre Ytesmcnutn Rpriso E.G
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by HZB Repository Antiferromagnetic structure and electronic properties of BaCr2As2 and BaCrFeAs2 Kai A. Filsinger,1 Walter Schnelle,1 Peter Adler,1 Gerhard H. Fecher,1 Manfred Reehuis,2 Andreas Hoser,2 Jens-Uwe Hoffmann,2 Peter Werner,3 Martha Greenblatt,4 and Claudia Felser1 1Max Planck Institute for Chemical Physics of Solids, N¨othnitzer Straße 40, 01187 Dresden, Germany 2Helmholtz-Zentrum Berlin f¨ur Materialien und Energie, 14109 Berlin, Germany 3Max Planck Institute of Microstructure Physics, Weinberg 2, 06120 Halle (Saale), Germany 4Department of Chemistry and Chemical Biology, Rutgers University, Piscataway, NJ, USA (Dated: January 13, 2017) The chromium arsenides BaCr2As2 and BaCrFeAs2 with ThCr2Si2 type structure (space group I4/mmm; also adopted by ‘122’ iron arsenide superconductors) have been suggested as mother com- pounds for possible new superconductors. DFT-based calculations of the electronic structure evi- dence metallic antiferromagnetic ground states for both compounds. By powder neutron diffraction we confirm for BaCr2As2 a robust ordering in the antiferromagnetic G-type structure at TN = 580 K with µCr = 1.9 µB at T = 2 K. Anomalies in the lattice parameters point to magneto-structural cou- pling effects. In BaCrFeAs2 the Cr and Fe atoms randomly occupy the transition-metal site and 57 G-type order is found below 265 K with µCr/Fe = 1.1 µB. Fe M¨ossbauer spectroscopy demonstrates that only a small ordered moment is associated with the Fe atoms, in agreement with electronic structure calculations with µFe ∼ 0. The temperature dependence of the hyperfine field does not follow that of the total moments.
    [Show full text]
  • 14Th International Ceramics Congress June 4-8/2018 Forum on New Materials June 10-14/2018
    Astract Deadline • October 15, 2017 Perugia - Italy • June 4-14/2018 14th International Ceramics Congress June 4-8/2018 8th Forum on New Materials June 10-14/2018 www.cimtec-congress.org Benedetto Bonfigli, Porta Marzia in Perugia, XV sec. Invitation to Attend! CIMTEC 2018 - 14th International Conference on Modern Materials and Technologies - will be held in Peru- gia, Italy, June 4 to 14, 2018. CIMTEC 2018 will consist of the 14th International Ceramics Congress (June 4-8) and of the 8th Forum on New Materials (June 10-14), each of them including a number of Symposia, Special Sessions, and Conferences. As a major longstanding event for the international materials community, CIMTEC will again gather together a large and qualified audience of materials scientists, physicists, chemists and engineers and of experts of a wide range of the most demanding application areas of modern materials, from the molecular and nanoscales to large complex integrated systems. The National Research Council of Italy (CNR), the Italian National Agency for New Technology, Energy and the Environment (ENEA) will act as major endorsers of CIMTEC 2018 together with the World Academy of Ceramics (WAC), The International Ceramic Federation (ICF) and the International Union of the Materials Research Societies (IUMRS). The Chair, Co-Chairs and CIMTEC 2018 Committees invite you to foster the progress in the field by contrib- uting with your expertise to what promises to be a very comprehensive and exciting meeting, and to enjoy the immense unique artistic heritage and wonderful landscape of Umbria district. Pietro Vincenzini Co-Chairs CIMTEC 2018 General Chair CIMTEC Conferences Gary Messing National Research Council, Italy Penn State University, USA World Academy of Ceramics Takashi Goto Tohoku University, Japan International Ceramic Federation Robert P.H.
    [Show full text]
  • Underpinning of Soviet Industrial Paradigms
    Science and Social Policy: Underpinning of Soviet Industrial Paradigms by Chokan Laumulin Supervised by Professor Peter Nolan Centre of Development Studies Department of Politics and International Studies Darwin College This dissertation is submitted for the degree of Doctor of Philosophy May 2019 Preface This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration except as declared in the Preface and specified in the text. It is not substantially the same as any that I have submitted, or, is being concurrently submitted for a degree or diploma or other qualification at the University of Cambridge or any other University or similar institution except as declared in the Preface and specified in the text. I further state that no substantial part of my dissertation has already been submitted, or, is being concurrently submitted for any such degree, diploma or other qualification at the University of Cambridge or any other University or similar institution except as declared in the Preface and specified in the text It does not exceed the prescribed word limit for the relevant Degree Committee. 2 Chokan Laumulin, Darwin College, Centre of Development Studies A PhD thesis Science and Social Policy: Underpinning of Soviet Industrial Development Paradigms Supervised by Professor Peter Nolan. Abstract. Soviet policy-makers, in order to aid and abet industrialisation, seem to have chosen science as an agent for development. Soviet science, mainly through the Academy of Sciences of the USSR, was driving the Soviet industrial development and a key element of the preparation of human capital through social programmes and politechnisation of the society.
    [Show full text]
  • Neutron Scattering Principal Investigators' Meeting
    Neutron Scattering Principal Investigators’ Meeting July 28-30, 2014 Hilton Washington DC North/Gaithersburg Gaithersburg, Maryland Office of Basic Energy Sciences Division of Materials Sciences and Engineering On the Cover Top Left: Numerical simulation of the magnetic inhomogeneity (red = magnetism, blue = superconductivity) caused by replacing 1% of the indium atoms in a superconductor (CeCoIn5) with cadmium atoms. The field of view is approximately 100 nanometers along each edge (Cover Image from Seo et al., Nature Physics, 10, 120–125, 2014). Top Middle: Resonant scattering with coherent x-rays on the size and the dynamics of magnetic domains in a Dysprosium crystal with three different domains (shown in three colors in the schematic). Above 85K, this material exhibits a spiral magnetic state wherein the magnetic moments in a given layer in each domain are parallel, but oriented at a fixed angle with respect to the moments in the adjacent layers (Cover Image from Chen et al., Physics Review Letters, 110, 217201, 2013). Top Right: Schematic illustration of cylinder-forming diblock copolymers, where the first block is a protein at the surface and the second block is the covalently attached synthetic polymer at the interior (Cover Image from Lam and Olsen, Soft Matter, 9, 2392–2402, 2013). Bottom Left: Inelastic neutron scattering of high-quality single-crystal samples of the mineral ZnCu3(OD)6Cl2 revealed that the scattered neutrons have a broad spread of energies (light green diffuse regions in figure), a hallmark signature predicted by theory (Han et al., Nature, 492, 406–410, 2012). Bottom Middle: High-energy x-ray diffraction pattern from a single grain of a gadolinium – cadmium alloy (shown in center) displaying the novel five-fold rotational symmetry, characteristic of an icosahedral quasicrystal.
    [Show full text]
  • Tt 40.1–40.18
    Thursday TT 40: Superconductivity: Ferropnictides 1 Time: Thursday 14:00–19:00 Location: HSZ 03 TT 40.1 Thu 14:00 HSZ 03 sruhe, Institut f¨urFestk¨orperphysik, 76021 Karlsruhe, Germany — Antiferromagnetic correlations in the normal state of 2Physikalisches Institut, Universit¨atKarlsruhe, 76128 Karlsruhe, Ger- LaFeAsO1−xFx with 0 ≤ x ≤ 0.125 — •Rudiger¨ Klingeler, Nor- many man Leps, Liran Wang, Christian Hess, Gunter¨ Behr, Vladislav Since the discovery of the new high-Tc iron pnictides, many scenar- Kataev, and Bernd Buchner¨ — IFW Dresden, P.O. Box 270116, ios were put forward to describe the symmetry of the order parameter 01171 Dresden, Germany including d-wave and unconventional s-wave. Early heat capacity mea- We have studied the interplay of magnetism and superconductivity in surements suggested that the electron-doped 1111 compounds show a LaFeAsO1−xFx with 0 ≤ x ≤ 0.125. For low doping with x ≤ 0.04, our nodal gap, while K-hole-doped 122 materials are fully gapped. Here we data confirm a moderate suppression of both the structural transition present a critical analysis of our own specific-heat data on Co-doped and the antiferromagnetic spin density wave formation. For x ≥ 0.05, 122 single crystals, in which we pay particular attention to the details both anomalies are completely suppressed and superconductivity is ob- of the phonon background subtraction as well as to the contribution served. Remarkably, the temperature dependence of the normal state of impurity phases. We also discuss an interesting field-dependence of susceptibility well above TC is almost independent of doping, i.e. both the thermal expansivity below Tc(H).
    [Show full text]
  • Spin Dynamics in 122-Type Iron-Based Superconductors
    Spin Dynamics in 122-Type Iron-Based Superconductors Von der Fakultät Mathematik und Physik der Universität Stuttgart zur Erlangung der Würde eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigte Abhandlung vorgelegt von Jitae Park aus Seoul (Südkorea) Hauptberichter: Prof. Dr. Bernhard Keimer Mitberichter: Prof. Dr. Harald Giessen Tag der mündlichen Prüfung: 16. Juli 2012 Max-Planck-Institut für Festkörperforschung Stuttgart 2012 Contents Zusammenfassung in deutscher Sprache 3 1 Introduction 7 1.1 General overview . 7 1.2 Scope of thesis . 9 2 Iron-based superconductors 13 2.1 Basic characteristics . 13 2.1.1 Zoo of iron-based superconductors . 13 2.1.2 Crystal structure and reciprocal-space structure . 14 2.1.3 Electronic band structure . 18 2.2 Phase diagram . 21 2.2.1 External parameters for modification of the system . 22 2.2.2 Long-range magnetic order and its spin dynamics . 27 2.2.3 Coexistence of magnetic and superconducting phases . 31 2.2.4 Spin dynamics in the parent compound . 34 2.3 Superconducting properties . 42 2.3.1 Pairing symmetry . 43 Δ/ 2.3.2 Coupling constant 2 kB Tc ...................... 45 2.4 Magnetic resonant mode in the spin-excitation spectra . 47 2.4.1 Theoretical approach . 48 2.4.2 Experimental observations . 49 3 Experimental methods 51 3.1 Preparation of single crystalline samples . 51 3.1.1 Flux method for single crystal growth . 51 3.1.2 Sample characterization . 54 3.2 Neutron scattering technique . 59 3.2.1 Scattering formulae . 60 3.2.2 Triple-axis neutron spectrometer . 70 3.2.3 Spurions .
    [Show full text]
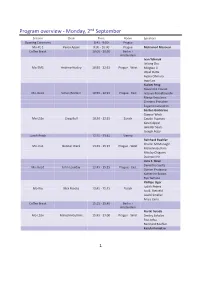
  • Program Overview ‐ Monday, 2ⁿd September
    Program overview ‐ Monday, 2ⁿd September Session Chair Time Room Speakers Opening Ceremony 8:45 ‐ 9:00 Prague Mo‐PL 1 Karen Appel 9:00 ‐ 10:00 Prague Mohamed Mezouar Coffee Break 10:00 ‐ 10:30 Berlin + Amsterdam Ivan Yahniuk Jinlong Zhu Mo‐EM1 Andrew Huxley 10:30 ‐ 12:15 Prague ‐ West Mingtao Li Utpal Dutta Ayako Ohmura Ingo Loa Xialoei Feng Alexandre Courac Mo‐Geo1 Simon Redfern 10:30 ‐ 12:15 Prague ‐ East Tetsuya Komabayashi Marija Krstulovic Clemens Prescher Eugenio Calandrini Gaston Garbarino Gunnar Weck Mo‐LS1x Craig Bull 10:30 ‐ 12:15 Zürich Catalin Popescu Karen Appel Jennifer Sears Joseph Boby Lunch Break 12:15 ‐ 13:45 Vienna Reinhard Boehler Charlie McMonagle Mo‐Ins1 Gunnar Weck 13:45 ‐ 15:15 Prague ‐ West Malcolm Guthrie Nikolay Chigarev Duanwei He Livia E. Bove Demetrio Scelta Mo‐Geo2 John Loveday 13:45 ‐ 15:15 Prague ‐ East Ciprian Pruteanu Katherine Brown Ryo Yamane Phillipe Oger Judith Peters Mo‐Bio Nick Brooks 13:45 ‐ 15:15 Zürich Ivo B. Rietveld László Smeller Anais Cario Coffee Break 15:15 ‐ 15:45 Berlin + Amsterdam Noriki Terada Mo‐LS2n Malcolm Guthrie 15:45 ‐ 17:00 Prague ‐ West Dmitry Sokolov Pau Jorba Reinhard Boehler Kazuki Komatsu 1 Program overview ‐ Monday, 2ⁿd September Mo‐Geo3 Livia E. Bove 15:45 ‐ 17:00 Prague ‐ East Samuele Fanetti Dane Sterbentz Sooheyong Lee Kateřina Štulíková Mo‐Food Jorge Saraiva 15:45 ‐ 17:00 Zürich Concepción P. Lamela Izabela Porębska Milan Houška Poster Session 1 17:00 ‐ 18:45 Berlin 8:45 ‐ 9:00 Opening Ceremony Room Prague 9:00 ‐ 10:00 Plenary Lecture 1 Room Prague Chair Karen Appel
    [Show full text]
  • Superconductivity, Magnetism and Crystal Chemistry of Ba1-Xkxfe2as2
    Superconductivity, magnetism and crystal chemistry of Ba1−xKxFe2As2 Dirk Johrendta,* and Rainer Pöttgenb a Department Chemie und Biochemie, Ludwig-Maximilians-Universität München, Butenandtstrasse 5–13 (Haus D), 81377 München, Germany E-mail: [email protected] b Institut für Anorganische und Analytische Chemie and NRW Graduate School of Chemistry, Universität Münster, Corrensstrasse 30, 48149 Münster, Germany E-mail: [email protected] A B S T R A C T BaFe2As2 is the parent compound of the ‘122’ iron arsenide superconductors and crystallizes with the tetragonal ThCr2Si2 type structure, space group I4/mmm. A spin density wave transition at 140 K is accompanied by a symmetry reduction to space group Fmmm and simultaneously by antiferromagnetic ordering. Hole-doping induces superconductivity in Ba1−xKxFe2As2 with a maximum Tc of 38 K at x ≈ 0.4. The upper critical fields approach 75 T with rather small anisotropy of Hc2. At low potassium concentrations (x ≤ 0.2), superconductivity apparently co-exists with the orthorhombic distorted and magnetically ordered phase. At doping levels x ≥ 0.3, the structural distortion and antiferromagnetic ordering is completely suppressed and the Tc is maximized. No magnetically ordered domains could be detected in optimally doped 57 Ba1−xKxFe2As2 (x ≥ 0.3) by Fe-Mössbauer spectroscopy in contrast µSR results obtained with single crystals. The magnetic hyperfine interactions investigated by 57Fe Mössbauer spectroscopy are discussed and compared to the ZrCuSiAs-type materials. 57 Keywords: BaFe2As2, Superconductivity, SDW anomaly, Fe-Mössbauer spectroscopy PACS: 74.10.+v, 74.25.Ha, 74.25.Dw, 74.62.Bf, 33.45.+x *Corresponding author. E-mail address: [email protected] (D.
    [Show full text]
  • Arxiv:1701.03127V1 [Cond-Mat.Supr-Con] 11 Jan 2017 Scnre Ytesmcnutn Rpriso E.G
    Antiferromagnetic structure and electronic properties of BaCr2As2 and BaCrFeAs2 Kai A. Filsinger,1 Walter Schnelle,1 Peter Adler,1 Gerhard H. Fecher,1 Manfred Reehuis,2 Andreas Hoser,2 Jens-Uwe Hoffmann,2 Peter Werner,3 Martha Greenblatt,4 and Claudia Felser1 1Max Planck Institute for Chemical Physics of Solids, N¨othnitzer Straße 40, 01187 Dresden, Germany 2Helmholtz-Zentrum Berlin f¨ur Materialien und Energie, 14109 Berlin, Germany 3Max Planck Institute of Microstructure Physics, Weinberg 2, 06120 Halle (Saale), Germany 4Department of Chemistry and Chemical Biology, Rutgers University, Piscataway, NJ, USA (Dated: September 9, 2021) The chromium arsenides BaCr2As2 and BaCrFeAs2 with ThCr2Si2 type structure (space group I4/mmm; also adopted by ‘122’ iron arsenide superconductors) have been suggested as mother com- pounds for possible new superconductors. DFT-based calculations of the electronic structure evi- dence metallic antiferromagnetic ground states for both compounds. By powder neutron diffraction we confirm for BaCr2As2 a robust ordering in the antiferromagnetic G-type structure at TN = 580 K with µCr = 1.9 µB at T = 2 K. Anomalies in the lattice parameters point to magneto-structural cou- pling effects. In BaCrFeAs2 the Cr and Fe atoms randomly occupy the transition-metal site and 57 G-type order is found below 265 K with µCr/Fe = 1.1 µB. Fe M¨ossbauer spectroscopy demonstrates that only a small ordered moment is associated with the Fe atoms, in agreement with electronic structure calculations with µFe ∼ 0. The temperature dependence of the hyperfine field does not follow that of the total moments. Both compounds are metallic but show large enhancements of the linear specific heat coefficient γ with respect to the band structure values.
    [Show full text]
  • APS Science 2009
    APS Science 2009 Science APS Advanced Photon Source ANL-10/06 ISSN 1931-5015 Argonne National Laboratory May 2010 9700 South Cass Avenue Argonne, IL 60439 USA May 2010 May www.anl.gov www.aps.anl.gov APS Science 2009 Argonne National Laboratory ANL-10/06 ISSN ANL-10/06 1931-5007 Research and Engineering Highlights from the Advanced Photon Source at Argonne National Laboratory U.S. DEPARTMENT OF ENERGY Argonne National Laboratory is a U.S. Department of Energy laboratory managed by UChicago Argonne, LLC ANL-10/06 ISSN 1931-5015 May 2010 The Advanced Photon Source at Argonne National Laboratory is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-ACO2-06CH11357 About Argonne National Laboratory Argonne is a U.S. Department of Energy laboratory managed by UChicago Argonne, LLC under contract DE-ACO2-06CH11357. The Laboratory’s main facility is outside Chicago, at 9700 South Cass Avenue, Argonne, Illinois 60439. For information about Argonne and its pioneering science and technology programs, see www.anl.gov. Availability of This Report This report is available, at no cost, at http://www.osti.gov/bridge. It is also available on paper to the U.S. Department of Energy and its contractors, for a processing fee, from: U.S. Department of Energy Office of Scientific and Technical Information P.O. Box 62 Oak Ridge, TN 37831-0062 phone (865) 576-8401 fax (865) 576-5728 [email protected] Disclaimer This report was prepared as an account of work sponsored by an agency of the United States Government.
    [Show full text]
  • 55 Th EHPRG Guide.Pdf
    www.ehprg2017.org 55th European High Pressure Research Group Meeting: High Pressure Science and Technology PROGRAMME 1 55th EHPRG Poznań, 3-8 September 2017 Programme Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Programme Overview Time schedule Time schedule 3 September 2017 4 September 2017 5 September 2017 6 September 2017 7 September 2017 8 September 2017 8.00-8.30 Registration 8.00-8.30 Registration Registration Special Session: Morasko Registration 8.30-9.00 Opening Ceremony 8.45 8.30-9.00 Meteorite Reserve 9.00-9.30 PL2 - Natalia 9.00-9.30 PL1 - Ho-Kwang Mao PL3 - Chris Michiels Mirosław Makohonienko PL5 - Przemysław Dera Dubrovinskaia Room 2.64 Room 2.64 Start in Room 2.64 Room 2.64 9.30-10.00 Room 2.64 9.30-10.00 10.00-10.30 Coffee Break Coffee Break Coffee Break Coffee Break Coffee Break 10.00-10.30 10.30-11.00 S 1 S 2 S 3 S 6 S 9 S 10 S 11 S 12 S 17 S 18 S 20 S 22 S 23 S 24 S 26 S 27 S 28 10.30-11.00 11.00-11.30 2.64 2.61 3.65 2.62 2.62 2.61 3.65 2.64 3.65 2.62 2.64 2.62 3.65 2.64 2.62 3.65 2.64 11.00-11.30 11.30-12.00 11.30-12.00 12.00-12.30 12.00-12.30 12.30-13.00 Lunch Break/Special Closing Ceremony 12.40 12.30-13.00 Lunch Break EHPRG General Session: “Women Under 13.00-13.30 Lunch Break Assembly 13.00-13.30 Pressure gathering” Room 2.64 Lunch 13.30-14.00 EHPRG Group Photo Room 2.57 13.30-14.00 14.00-14.30 S 5 S 4 S 7 S 8 S 13 S 14 S 15 S 16 PL4 - Elena Boldyreva 14.00-14.30 Lunch Break 14.30-15.00 2.64 2.61 3.65 2.62 3.65 2.61 2.64 2.62 Room 2.64 14.30-15.00 15.00-15.30 15.00-15.30 15.30-16.00 Poster Session 2 15.30-16.00
    [Show full text]
  • High-Pressure Effects on Isotropic Superconductivity in the Iron-Free Layered Pnictide Superconductor Bapd2as2
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Kyutacar : Kyushu Institute of Technology Academic Repository High-pressure effects on isotropic superconductivity in the iron-free layered pnictide superconductor BaPd2As2 著者 Abdel-Hafiez M., Zhao Y., Huang Z., Cho C.-w., Wong C. H., Hassen A., Ohkuma M., Fang Y.-W., Pan B.-J., Ren Z.-A., Sadakov A., Usoltsev A., Pudalov V., Mito M., Lortz R., Krellner C., Yang W. journal or Physical Review B publication title volume 97 number 13 page range 134508-1-134508-9 year 2018-04-12 URL http://hdl.handle.net/10228/00007071 doi: info:doi/10.1103/PhysRevB.97.134508 PHYSICAL REVIEW B 97, 134508 (2018) High-pressure effects on isotropic superconductivity in the iron-free layered pnictide superconductor BaPd2As2 M. Abdel-Hafiez,1,2,3,* Y. Zhao,4 Z. Huang,5 C.-w. Cho,5 C. H. Wong,6 A. Hassen,7 M. Ohkuma,8 Y.-W. Fang,9 B.-J. Pan,10 Z.-A. Ren,10 A. Sadakov,11 A. Usoltsev,11 V. Pudalov,11 M. Mito,8 R. Lortz,5 C. Krellner,2 and W. Yang4,12 1Center for High Pressure Science and Technology Advanced Research, Beijing, 100094, China 2Institute of Physics, Goethe University Frankfurt, 60438 Frankfurt/M, Germany 3National University of Science and Technology “MISiS,” Moscow 119049, Russia 4Center for High Pressure Science and Technology Advanced Research, Shanghai, 201203, China 5Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong 6Institute of Physics and Technology, Ural Federal University, Yekaterinburg, Russia 7Faculty of Science, Physics Department, Fayoum University, 63514-Fayoum, Egypt 8Graduate School of Engineering, Kyushu Institute of Technology, Kitakyushu 804-8550, Japan 9Key Laboratory of Polar Materials and Devices, Ministry of Education, Department of Electronic Engineering, East China Normal University, Shanghai 200241, China 10Institute of Physics and Beijing National Laboratory for Condensed Matter Physics, Chinese Academy of Sciences, Beijing 100190, China 11P.N.
    [Show full text]