DOCSLIB.ORG

Types of Functions Algebraic Functions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Types of Functions Algebraic Functions MATH 1170 Chapter 1 Worksheet #1 NAME Note: It I bolded and underlined a term, you are responsible for a verbadom definition of that term (as well as understanding that definition). If I just bolded a term, I only expect that you are comfortable with the use of and using that term (i.e. understanding it). Types of Functions Now that we have discussed what functions are and some of their characteristics, we will explore different types of fumctions. Section 1.2 of the text outlines a variety of types of functions. Notice that since the following are all functions, they will all pass the Vertical Line Test. Algebraic Functions A function is called an algebraic function if it can be constructed using algebraic operations (such as addition, subtraction, multiplication, division and taking roots). Polynomials, power functions, and rational function are all algebraic functions. 1 Polynomials A function p is a polynomial if n n−1 2 p(x) = anx + an−1x + ::: + a2x + a1x + a0 where n is a nonnegative integer and a0; a1; a2; :::; an−1; an are all constants called coefficients of the polynomial. If the leading coefficient an 6= 0 then the degree of p(x) is n. • A polynomial of degree 1 is called a linear function. • A polynomial of degree 2 is called a quadratic function. • A polynomial of degree 3 is called a cubic function. • A polynomial of degree 4 is called a quartic function. • A polynomial of degree 5 is called a quintic function. • ...and so on... We often talk about finding roots of a polynomial. This means we are finding where the graph of the function hits the x-axis. Finding the roots of a polynomial entails setting the polynomial equal to zero and solving for x. Find the roots of p(x) = x2 − x − 6: 1 Linear Functions The most famous polynomial is the linear function. y is said to be a linear function of x if the graph of the function is a line so that we can use the slope-intercept form of the equation of a line to write a formula for the function as y = mx + b where m is the slope and b is the y-intercept. If this is the case, what do m and b equal in the p(x) equation? Graph the family of equations f(x) = x+b where be is an integer b = −2; −1; 0; 1; 2 on the same coordinate system. Graph the family of equations f(x) = mx where be is an integer m = −2; −1; 0; 1; 2 on the same coordinate system. Find the equation for a line that passes through (2; −1) and (3; 5). 2 Power Functions A function of the form f(x) = xa where a is a constant is called a power function. The power function takes a variety of forms based on the type of constant that a is. These different forms arrise when • 2.1 a = n where is n a positive integer, • 2.2 a = 1=n where n is a positive integer, and • 2.3 a = −1. We will explore these forms in the following sections. 2 2.1 If a = n where n is a positive integer... Notice that is n is a positive integer then the power function is really just a type of polynomial. Using your graphing calculator, sketch a graph of the following functions: 2 a. f1(x) = x b. f2(x) = x 3 4 c. f3(x) = x d. f4(x) = x 5 6 e. f5(x) = x f. f6(x) = x When n is odd, • what is the domain of f(x) = xn? • what is the range of f(x) = xn? • where is f(x) = xn increasing? • where is f(x) = xn decreasing? • How do you know that these characteristics will hold for every odd n? When n is even, • what is the domain of f(x) = xn? • what is the range of f(x) = xn? • where is f(x) = xn increasing? • where is f(x) = xn decreasing? • How do you know that these characteristics will hold for every even n? 3 2.2 If a = 1=n where n is a positive integer... The functions of the form f(x) = x1=n are called root functions. It is important to note that root functions are the inverses of polynomial functions. But what does this mean? Recall the definition of an inverse function from one of our previous lectures. (It can also be found on page 62 of the Stewart text.) What does it mean to say that root functions are the inverses of polynomial functions? Demonstrate that g(x) = x1=2 is the inverse function of f(x) = x2. Write f(x) = x1=n in a different form. Is f(x) = x1=n, where n is a positive integer, a polynomial? Using your graphing calculator as a tool, sketch a graph of the following functions: 1=2 1=3 a. f2(x) = x b. f3(x) = x 1=4 1=5 c. f4(x) = x d. f5(x) = x When n is odd, • what is the domain of f(x) = x1=n? • what is the range of f(x) = x1=n? • where is f(x) = x1=n increasing? • where is f(x) = x1=n decreasing? • How do you know that these characteristics will hold for every odd n? 4 When n is even, • what is the domain of f(x) = x1=n? • what is the range of f(x) = x1=n? • where is f(x) = x1=n increasing? • where is f(x) = x1=n decreasing? • How do you know that these characteristics will hold for every even n? 2.3 If a = −1... In this case, f(x) = x−1 is the reciprocal function. Is f(x) = x−1 a polynomial? Using your graphing calculator as a tool, sketch a graph of f(x) = x−1 and describe the domain, range and intervals of increasing and decreasing: Domain: Range: Increasing: Decreasing: 3 Rational Functions Moving on from power functions, we will now explore our last type of algebraic function: the rational function. A rational function is a ratio of two polynomials, p(x) and q(x): p(x) f(x) = q(x) Which of the previously mentioned functions is a rational function? What happens when you evaluate this function at x = 0? 5 x−1 Consider f(x) = x2−4 . • Identify p(x) and q(x). • Using your graphing calculator, sketch a graph of f(x). • What happens at x = 2 and x = −2? Why? Exponential Functions The exponential functions are the functions of the form f(x) = ax, where the base a is a positive constant. Note that these function are called exponential functions because the variable, x, is in the exponent. Using your graphing calculator as a tool, sketch a graph of the following functions and describe the domain, range and intervals of increasing and decreasing: a. f(x) = 2x b. f(x) = (1=2)x c. f(x) = 3x d. f(x) = (1=3)x When a > 1, • what is the domain of f(x) = ax? • what is the range of f(x) = ax? • where is f(x) = ax increasing? • where is f(x) = ax decreasing? • How do you know that these characteristics will hold for every a > 1? 6 When 0 < a < 1, • what is the domain of f(x) = ax? • what is the range of f(x) = ax? • where is f(x) = ax increasing? • where is f(x) = ax decreasing? • How do you know that these characteristics will hold for every 0 < a < 1? What is the difference between the function f(x) = x2 and g(x) = 2x? Find the exponential function f(x) = ax whose graph goes through the point (−4; 1=16): Logarithmic Functions The logarithmic functions, f(x) = logax, where the base a is a positive constant, are the functions that are the inverse of the exponential functions. It is important to realize that logarithmic functions are the inverses of exponential functions. x What does it mean to say that f(x) = logax is the inverse of g(x) = a ? x Show that f(x) = log2x is the inverse of g(x) = 2 .(Hint: This may require you to use the laws of logarithms that can be found on page 65 on Stewart.) 7 Using your graphing calculator as a tool, sketch a graph of the following functions and describe the domain, range and intervals of increasing and decreasing: a. f(x) = log2x b. f(x) = log10x Domain: Domain: Range: Range: Increasing: Increasing: Decreasing: Decreasing: Trigonometric Functions Using your graphing calculator as a tool, sketch a graph of the following functions and describe the domain, range and intervals of increasing and decreasing: a. f(x) = sinx b. f(x) = cosx c. f(x) = tanx Domain: Domain: Domain: Range: Range: Range: Increasing: Increasing: Increasing: Decreasing: Decreasing: Decreasing What do you notice about the graph of: • f(x) = sin(x + π=2)? • f(x) = sin(x + 2π)? 8 Piecewise Functions Piecewise functions are defined to be one of the above types of functions on one part of the x-axis and another function on a different part of the x-axis. For example consider ( x + 1; if x ≤ 1 f(x) = x2; if x > 1 This function has the same outputs as g(x) = x + 1 for x values less than of equal to 1 (the left half of the graph) and looks like h(x) = x2 for x greater than 1 (the right half of the graph). Sketch a graph of f(x). Find f(−2).
Load more

Recommended publications
  • Field Theory Pete L. Clark
    Field Theory Pete L. Clark Thanks to Asvin Gothandaraman and David Krumm for pointing out errors in these notes. Contents About These Notes 7 Some Conventions 9 Chapter 1. Introduction to Fields 11 Chapter 2. Some Examples of Fields 13 1. Examples From Undergraduate Mathematics 13 2. Fields of Fractions 14 3. Fields of Functions 17 4. Completion 18 Chapter 3. Field Extensions 23 1. Introduction 23 2. Some Impossible Constructions 26 3. Subfields of Algebraic Numbers 27 4. Distinguished Classes 29 Chapter 4. Normal Extensions 31 1. Algebraically closed fields 31 2. Existence of algebraic closures 32 3. The Magic Mapping Theorem 35 4. Conjugates 36 5. Splitting Fields 37 6. Normal Extensions 37 7. The Extension Theorem 40 8. Isaacs' Theorem 40 Chapter 5. Separable Algebraic Extensions 41 1. Separable Polynomials 41 2. Separable Algebraic Field Extensions 44 3. Purely Inseparable Extensions 46 4. Structural Results on Algebraic Extensions 47 Chapter 6. Norms, Traces and Discriminants 51 1. Dedekind's Lemma on Linear Independence of Characters 51 2. The Characteristic Polynomial, the Trace and the Norm 51 3. The Trace Form and the Discriminant 54 Chapter 7. The Primitive Element Theorem 57 1. The Alon-Tarsi Lemma 57 2. The Primitive Element Theorem and its Corollary 57 3 4 CONTENTS Chapter 8. Galois Extensions 61 1. Introduction 61 2. Finite Galois Extensions 63 3. An Abstract Galois Correspondence 65 4. The Finite Galois Correspondence 68 5. The Normal Basis Theorem 70 6. Hilbert's Theorem 90 72 7. Infinite Algebraic Galois Theory 74 8. A Characterization of Normal Extensions 75 Chapter 9.
    [Show full text]
  • On the Number of Cubic Orders of Bounded Discriminant Having
    On the number of cubic orders of bounded discriminant having automorphism group C3, and related problems Manjul Bhargava and Ariel Shnidman August 8, 2013 Abstract For a binary quadratic form Q, we consider the action of SOQ on a two-dimensional vector space. This representation yields perhaps the simplest nontrivial example of a prehomogeneous vector space that is not irreducible, and of a coregular space whose underlying group is not semisimple. We show that the nondegenerate integer orbits of this representation are in natural bijection with orders in cubic fields having a fixed “lattice shape”. Moreover, this correspondence is discriminant-preserving: the value of the invariant polynomial of an element in this representation agrees with the discriminant of the corresponding cubic order. We use this interpretation of the integral orbits to solve three classical-style count- ing problems related to cubic orders and fields. First, we give an asymptotic formula for the number of cubic orders having bounded discriminant and nontrivial automor- phism group. More generally, we give an asymptotic formula for the number of cubic orders that have bounded discriminant and any given lattice shape (i.e., reduced trace form, up to scaling). Via a sieve, we also count cubic fields of bounded discriminant whose rings of integers have a given lattice shape. We find, in particular, that among cubic orders (resp. fields) having lattice shape of given discriminant D, the shape is equidistributed in the class group ClD of binary quadratic forms of discriminant D. As a by-product, we also obtain an asymptotic formula for the number of cubic fields of bounded discriminant having any given quadratic resolvent field.
    [Show full text]
  • Robust Algorithms for Object Localization
    Robust Algorithms for Ob ject Lo calizati on y Dinesh Mano cha Aaron S. Wallack Department of Computer Science Computer Science Division University of North Carolina University of California Chap el Hill, NC 27599-3175 Berkeley, CA 94720 mano [email protected] wallack@rob otics.eecs.b erkeley.edu Abstract Ob ject lo calization using sensed data features and corresp onding mo del features is a fun- damental problem in machine vision. We reformulate ob ject lo calization as a least squares problem: the optimal p ose estimate minimizes the squared error discrepancy b etween the sensed and predicted data. The resulting problem is non-linear and previous attempts to estimate the optimal p ose using lo cal metho ds such as gradient descent su er from lo cal minima and, at times, return incorrect results. In this pap er, we describ e an exact, accurate and ecient algorithm based on resultants, linear algebra, and numerical analysis, for solv- ing the nonlinear least squares problem asso ciated with lo calizing two-dimensional ob jects given two-dimensional data. This work is aimed at tasks where the sensor features and the mo del features are of di erenttyp es and where either the sensor features or mo del features are p oints. It is applicable to lo calizing mo deled ob jects from image data, and estimates the p ose using all of the pixels in the detected edges. The algorithm's running time dep ends mainly on the typ e of non-p oint features, and it also dep ends to a small extent on the number of features.
    [Show full text]
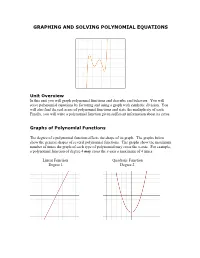
  • Graphing and Solving Polynomial Equations
    GRAPHING AND SOLVING POLYNOMIAL EQUATIONS Unit Overview In this unit you will graph polynomial functions and describe end behavior. You will solve polynomial equations by factoring and using a graph with synthetic division. You will also find the real zeros of polynomial functions and state the multiplicity of each. Finally, you will write a polynomial function given sufficient information about its zeros. Graphs of Polynomial Functions The degree of a polynomial function affects the shape of its graph. The graphs below show the general shapes of several polynomial functions. The graphs show the maximum number of times the graph of each type of polynomial may cross the x-axis. For example, a polynomial function of degree 4 may cross the x-axis a maximum of 4 times. Linear Function Quadratic Function Degree 1 Degree 2 Cubic Function Quartic Function Degree 3 Degree 4 Quintic Function Degree 5 Notice the general shapes of the graphs of odd degree polynomial functions and even degree polynomial functions. The degree and leading coefficient of a polynomial function affects the graph’s end behavior. End behavior is the direction of the graph to the far left and to the far right. The chart below summarizes the end behavior of a Polynomial Function. Degree Leading Coefficient End behavior of graph Even Positive Graph goes up to the far left and goes up to the far right. Even Negative Graph goes down to the far left and down to the far right. Odd Positive Graph goes down to the far left and up to the far right.
    [Show full text]
  • Math 2250 HW #10 Solutions
    Math 2250 Written HW #10 Solutions 1. Find the absolute maximum and minimum values of the function g(x) = e−x2 subject to the constraint −2 ≤ x ≤ 1. Answer: First, we check for critical points of g, which is differentiable everywhere. By the Chain Rule, 2 2 g0(x) = e−x · (−2x) = −2xe−x : Since e−x2 > 0 for all x, g0(x) = 0 when 2x = 0, meaning when x = 0. Hence, x = 0 is the only critical point of g. Now we just evaluate g at the critical point and the endpoints: 2 g(−2) = e−(−2) = e−4 = 1=e4 2 g(0) = e−0 = e0 = 1 2 g(2) = e−1 = e−1 = 1=e: Since 1 > 1=e > 1=e4, we see that the absolute maximum of g(x) on this interval is at (0; 1) and the absolute minimum is at (−2; 1=e4). 2. Find all local maxima and minima of the curve y = x2 ln x. Answer: Notice, first of all, that ln x is only defined for x > 0, so the function x2 ln x is likewise only defined for x > 0. This function is differentiable on its entire domain, so we differentiate in search of critical points. Using the Product Rule, 1 y0 = 2x ln x + x2 · = 2x ln x + x = x(2 ln x + 1): x Since we're only allowed to consider x > 0, we see that the derivative is zero only when 2 ln x + 1 = 0, meaning ln x = −1=2. Therefore, we have a critical point at x = e−1=2.
    [Show full text]
  • The Fast Quartic Solver Peter Strobach AST-Consulting Inc., Bahnsteig 6, 94133 Röhrnbach, Germany Article Info a B S T R a C T
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Journal of Computational and Applied Mathematics 234 (2010) 3007–3024 Contents lists available at ScienceDirect Journal of Computational and Applied Mathematics journal homepage: www.elsevier.com/locate/cam The fast quartic solver Peter Strobach AST-Consulting Inc., Bahnsteig 6, 94133 Röhrnbach, Germany article info a b s t r a c t Article history: A fast and highly accurate algorithm for solving quartic equations is introduced. This Received 27 February 2010 new algorithm is more than six times as fast and several times more accurate than the Received in revised form 14 April 2010 quasi-standard Companion matrix eigenvalue quartic solver. Moreover, the method is exceptionally robust in cases of extreme root spread. The new algorithm is based on MSC: a factorization of the quartic in two quadratics, which are solved in closed form. The 65E05 performance key at this point is a fixed-point iteration based fitting algorithm for backward Keywords: optimization of the underlying quartic-to-quadratic polynomial decomposition. Detailed Quartic function experimental results confirm our claims. Polynomial factorization ' 2010 Elsevier B.V. All rights reserved. Polynomial rooting Companion matrix Eigenvalues 1. Introduction Consider the practical rooting of quartic polynomials or functions of the type f .x/ D x4 C ax3 C bx2 C cx C d D x2 C αx C β x2 C γ x C δ D .x − x1/.x − x2/.x − x3/.x − x4/ : (1) A quartic solver is an algorithm that relates a set of real or complex conjugate or mixed real/complex conjugate roots fx1; x2; x3; x4g to a given set of real quartic coefficients fa; b; c; dg.
    [Show full text]
  • Section 1.2 – Mathematical Models: a Catalog of Essential Functions
    Section 1-2 © Sandra Nite Math 131 Lecture Notes Section 1.2 – Mathematical Models: A Catalog of Essential Functions A mathematical model is a mathematical description of a real-world situation. Often the model is a function rule or equation of some type. Modeling Process Real-world Formulate Test/Check problem Real-world Mathematical predictions model Interpret Mathematical Solve conclusions Linear Models Characteristics: • The graph is a line. • In the form y = f(x) = mx + b, m is the slope of the line, and b is the y-intercept. • The rate of change (slope) is constant. • When the independent variable ( x) in a table of values is sequential (same differences), the dependent variable has successive differences that are the same. • The linear parent function is f(x) = x, with D = ℜ = (-∞, ∞) and R = ℜ = (-∞, ∞). • The direct variation function is a linear function with b = 0 (goes through the origin). • In a direct variation function, it can be said that f(x) varies directly with x, or f(x) is directly proportional to x. Example: See pp. 26-28 of the text. 1 Section 1-2 © Sandra Nite Polynomial Functions = n + n−1 +⋅⋅⋅+ 2 + + A function P is called a polynomial if P(x) an x an−1 x a2 x a1 x a0 where n is a nonnegative integer and a0 , a1 , a2 ,..., an are constants called the coefficients of the polynomial. If the leading coefficient an ≠ 0, then the degree of the polynomial is n. Characteristics: • The domain is the set of all real numbers D = (-∞, ∞). • If the degree is odd, the range R = (-∞, ∞).
    [Show full text]
  • Supplement 1: Toolkit Functions
    Supplement 1: Toolkit Functions What is a Function? The natural world is full of relationships between quantities that change. When we see these relationships, it is natural for us to ask “If I know one quantity, can I then determine the other?” This establishes the idea of an input quantity, or independent variable, and a corresponding output quantity, or dependent variable. From this we get the notion of a functional relationship in which the output can be determined from the input. For some quantities, like height and age, there are certainly relationships between these quantities. Given a specific person and any age, it is easy enough to determine their height, but if we tried to reverse that relationship and determine age from a given height, that would be problematic, since most people maintain the same height for many years. Function Function: A rule for a relationship between an input, or independent, quantity and an output, or dependent, quantity in which each input value uniquely determines one output value. We say “the output is a function of the input.” Function Notation The notation output = f(input) defines a function named f. This would be read “output is f of input” Graphs as Functions Oftentimes a graph of a relationship can be used to define a function. By convention, graphs are typically created with the input quantity along the horizontal axis and the output quantity along the vertical. The most common graph has y on the vertical axis and x on the horizontal axis, and we say y is a function of x, or y = f(x) when the function is named f.
    [Show full text]
  • As1.4: Polynomial Long Division
    AS1.4: POLYNOMIAL LONG DIVISION One polynomial may be divided by another of lower degree by long division (similar to arithmetic long division). Example (x32+ 3 xx ++ 9) (x + 2) x + 2 x3 + 3x2 + x + 9 1. Write the question in long division form. 3 2. Begin with the x term. 2 x3 divided by x equals x2. x 2 Place x above the division bracket x+2 x32 + 3 xx ++ 9 as shown. subtract xx32+ 2 2 3. Multiply x + 2 by x . x2 xx2+=+22 x 32 x ( ) . Place xx32+ 2 below xx32+ 3 then subtract. x322+−+32 x x xx = 2 ( ) 4. “Bring down” the next term (x) as 2 x + x indicated by the arrow. +32 +++ Repeat this process with the result until xxx23x 9 there are no terms remaining. x32+↓2x 2 2 5. x divided by x equals x. x + x Multiply xx( +=+22) x2 x . xx2 +−1 ( xx22+−) ( x +2 x) =− x 32 x+23 x + xx ++ 9 6. Bring down the 9. xx32+2 ↓↓ 2 7. − x divided by x equals − 1. xx+↓ Multiply xx2 +↓2 −12( xx +) =−− 2 . −+x 9 (−+xx9) −−−( 2) = 11 −−x 2 The remainder is 11 +11 (x32+ 3 xx ++ 9) equals xx2 +−1, with remainder 11. (x + 2) AS 1.4 – Polynomial Long Division Page 1 of 4 June 2012 If the polynomial has an ‘xn ‘ term missing, add the term with a coefficient of zero. Example (2xx3 − 31 +÷) ( x − 1) Rewrite (2xx3 −+ 31) as (2xxx32+ 0 −+ 31) Divide using the method from the previous example. 2 22xx32÷= x 2xx+− 21 2 32 −= − 2xx( 12) x 2 x 32 x−12031 xxx + −+ 20xx32−=−−(22xx32) 2x2 2xx32− 2 ↓↓ 2 22xx÷= x 2xx2 −↓ 3 2xx( −= 12) x2 − 2 x 2 2 2 2xx−↓ 2 23xx−=−−22xx− x ( ) −+x 1 −÷xx =−1 −+x 1 −11( xx −) =−+ 1 0 −+xx1− ( + 10) = Remainder is 0 (2xx32− 31 +÷) ( x −= 1) ( 2 xx + 21 −) with remainder = 0 ∴(2xx32 − 3 += 1) ( x − 12)( xx + 2 − 1) See Exercise 1.
    [Show full text]
  • Fundamental Units and Regulators of an Infinite Family of Cyclic Quartic Function Fields
    J. Korean Math. Soc. 54 (2017), No. 2, pp. 417–426 https://doi.org/10.4134/JKMS.j160002 pISSN: 0304-9914 / eISSN: 2234-3008 FUNDAMENTAL UNITS AND REGULATORS OF AN INFINITE FAMILY OF CYCLIC QUARTIC FUNCTION FIELDS Jungyun Lee and Yoonjin Lee Abstract. We explicitly determine fundamental units and regulators of an infinite family of cyclic quartic function fields Lh of unit rank 3 with a parameter h in a polynomial ring Fq[t], where Fq is the finite field of order q with characteristic not equal to 2. This result resolves the second part of Lehmer’s project for the function field case. 1. Introduction Lecacheux [9, 10] and Darmon [3] obtain a family of cyclic quintic fields over Q, and Washington [22] obtains a family of cyclic quartic fields over Q by using coverings of modular curves. Lehmer’s project [13, 14] consists of two parts; one is finding families of cyclic extension fields, and the other is computing a system of fundamental units of the families. Washington [17, 22] computes a system of fundamental units and the regulators of cyclic quartic fields and cyclic quintic fields, which is the second part of Lehmer’s project. We are interested in working on the second part of Lehmer’s project for the families of function fields which are analogous to the type of the number field families produced by using modular curves given in [22]: that is, finding a system of fundamental units and regulators of families of cyclic extension fields over the rational function field Fq(t). In [11], we obtain the results for the quintic extension case.
    [Show full text]
  • Trigonometric Functions
    72 Chapter 4 Trigonometric Functions To define the radian measurement system, we consider the unit circle in the xy-plane: ........................ ....... ....... ...... ....................... .............. ............... ......... ......... ....... ....... ....... ...... ...... ...... ..... ..... ..... ..... ..... ..... .... ..... ..... .... .... .... .... ... (cos x, sin x) ... ... 4 ... A ..... .. ... ....... ... ... ....... ... .. ....... .. .. ....... .. .. ....... .. .. ....... .. .. ....... .. .. ....... ...... ....... ....... ...... ....... x . ....... Trigonometric Functions . ...... ....y . ....... (1, 0) . ....... ....... .. ...... .. .. ....... .. .. ....... .. .. ....... .. .. ....... .. ... ...... ... ... ....... ... ... .......... ... ... ... ... .... B... .... .... ..... ..... ..... ..... ..... ..... ..... ..... ...... ...... ...... ...... ....... ....... ........ ........ .......... .......... ................................................................................... An angle, x, at the center of the circle is associated with an arc of the circle which is said to subtend the angle. In the figure, this arc is the portion of the circle from point (1, 0) So far we have used only algebraic functions as examples when finding derivatives, that is, to point A. The length of this arc is the radian measure of the angle x; the fact that the functions that can be built up by the usual algebraic operations of addition, subtraction, radian measure is an actual geometric length is largely responsible for the usefulness of
    [Show full text]
  • Coefficients of Algebraic Functions: Formulae and Asymptotics
    COEFFICIENTS OF ALGEBRAIC FUNCTIONS: FORMULAE AND ASYMPTOTICS CYRIL BANDERIER AND MICHAEL DRMOTA Abstract. This paper studies the coefficients of algebraic functions. First, we recall the too-less-known fact that these coefficients fn always a closed form. Then, we study their asymptotics, known to be of the type n α fn ∼ CA n . When the function is a power series associated to a context-free grammar, we solve a folklore conjecture: the appearing critical exponents α belong to a subset of dyadic numbers, and we initiate the study the set of possible values for A. We extend what Philippe Flajolet called the Drmota{Lalley{Woods theorem (which is assuring α = −3=2 as soon as a "dependency graph" associated to the algebraic system defining the function is strongly connected): We fully characterize the possible singular behaviors in the non-strongly connected case. As a corollary, it shows that certain lattice paths and planar maps can not be generated by a context-free grammar (i.e., their generating function is not N-algebraic). We give examples of Gaussian limit laws (beyond the case of the Drmota{Lalley{Woods theorem), and examples of non Gaussian limit laws. We then extend our work to systems involving non-polynomial entire functions (non-strongly connected systems, fixed points of entire function with positive coefficients). We end by discussing few algorithmic aspects. Resum´ e.´ Cet article a pour h´erosles coefficients des fonctions alg´ebriques.Apr`esavoir rappel´ele fait trop peu n α connu que ces coefficients fn admettent toujours une forme close, nous ´etudionsleur asymptotique fn ∼ CA n .
    [Show full text]