DOCSLIB.ORG

U3SN2: Exploring Cubic Functions & Power Functions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
U3SN2: Exploring Cubic Functions & Power Functions U3SN2: Exploring Cubic Functions & Power Functions You should learn to: 1. Determine the general behavior of the graph of even and odd degree power functions. 2. Explore the possible graphs of cubic, quartic, and quintic functions, and extend graphical properties to higher-degree functions. 3. Generalize the key characteristics of polynomials. 4. Sketch the graph of any polynomial given key characteristics. � �−� A polynomial function is a function that can be written in the form �(�) = ��� + ��−�� + � ⋯ ��� + ��� + �� where ��, ��−1, …�2, �1, �0 are complex numbers and the exponents are nonnegative integers. The form shown here is called the standard form of a polynomial. Really this means it is a function of the form (�) = ��� + ����� , where n is a non-negative integer. Polynomial functions are continuous (there are no breaks in their graphs) and they only have smooth turns (there are no sharp turns). Polynomial functions also have a domain of all reals. Example 1. Are the following Polynomials? If not, why not? You already know that a second-degree polynomial function is called a quadratic function, and a third- degree polynomial function is called a cubic function. A quartic function is a fourth-degree polynomial function, while a quintic function is a fifth-degree polynomial function. Example 2. Graph and compare the following. y y y x x x � = � yx= 3 yx= 5 y y y x x x yx= 2 yx= 4 y = x6 What if we have a function with more than one power? Will it mirror the even behavior or the odd behavior? y y y x x x � = �5 + �4 � = �3 + �8 � = �2(� + 2) The degree of a polynomial function is the highest degree of its terms when written in standard form. Example 3. Find the degree of each of the polynomial functions below. A. � = 4�2 + 3�5 − 12� + 2 B. �(�) = −(� − 4)2(� + 2)3 C. � = �3(� − 1)(�2 − 5) Leading Coefficient Test: The end behavior of a graph of a function is the behavior of the graph as x approaches negative infinity and as x approaches positive infinity. DEGREE (highest power) End behavior of �(�) = ��� + ����� � is EVEN � is ODD where � is the degree of the polynomial. “�” is + In other words, � is the highest power! Leading Leading coefficient “�” is – Example 4. Use the degree and the leading coefficient to find the end behavior of the following functions. A. �(�) = 5�7 B. �(�) = −7�10 1 C. �(�) = ��7 D. �(�) = −27(�2 − 1)3(� + 2)7 3 Finding the �-intercepts of a polynomial function. How would we find the �-intercepts of these polynomial functions? How have we found these in the past? Example 5. Find the x-intercepts and the zeros for each of the polynomial functions, then use the idea of end behavior to sketch the graph of the function. B. �(�) = �3 + 4� A. �(�) = �3 − �2 − 2� y y x x ( ) 1 ( )( )2( )3 C. ℎ(�) = �(� + 3)(� − 4)(� + 1) D. � � = 10 � + 3 � − 2 � + 1 y y x x So, the rule for �-intercepts is that: on the graph of a polynomial function of degree �, it can have at most “�” �-intercepts. A zero of a function, �(�), is a number x which makes �(�) = 0. The real zeros of polynomial functions are the x-values of the x-intercept points. The polynomial function can have two types of behavior through the �-intercepts. It can “cross” or it can “bounce.” Looking at the last example, what is the determining factor of whether it crosses or bounces? Multiplicity is how many times a particular number is a zero for a given polynomial function. If the multiplicity is even the graph will “bounce” at that zero and if the multiplicity is odd the graph will “cross” at that zero. Example 6. Draw a rough sketch of the behavior at each of the zeros shown in the functions below. A. �(�) = (� + 4)3 B. �(�) = (� + 4)10 1 C. �(�) = �2(� + 1) D. �(�) = (� + 1)2(� − 1)2 3 Putting it all together! STEPS TO GRAPHING A POLYNOMIAL FUNCTION 1. Find end behavior determined by the degree and the “�” value. 2. Find the x-intercepts by setting �(�) = 0 and factoring or using the quadratic formula to solve. Remember, the multiplicity at each of these zeros causes our graph to “cross” if the power is odd, and “bounce” if the power is even. 3. Find the y-intercept. If it’s in standard form we can look at the constant, if it’s in another form we can find this by setting x = 0. 4. REMEMBER, the graph of a polynomial function is always smooth and continuous and beautiful, with no sharp turns. Remember the domain is all reals, so your graph should continue to the right and left FOREVER. Example 7. Graph the following functions (rough graphs) A. �(�) = −3�3 − 12�2 y x Degree: -4 -3 -2 -1 1 2 3 4 5 End Behavior: y-intercept: x-intercepts: B. �(�) = (�2 − 1)(� + 4)2 y x Degree: -4 -3 -2 -1 1 2 3 4 5 End Behavior: y-intercept: x-intercepts: C. Write a polynomial function having zeros of y � = 3, and � = −3 (multiplicity 2) x Degree: -4 -3 -2 -1 1 2 3 4 5 End Behavior: y-intercept: x-intercepts: .
Load more

Recommended publications
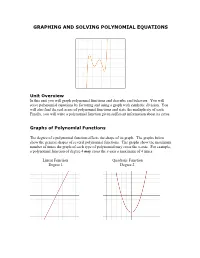
  • Graphing and Solving Polynomial Equations
    GRAPHING AND SOLVING POLYNOMIAL EQUATIONS Unit Overview In this unit you will graph polynomial functions and describe end behavior. You will solve polynomial equations by factoring and using a graph with synthetic division. You will also find the real zeros of polynomial functions and state the multiplicity of each. Finally, you will write a polynomial function given sufficient information about its zeros. Graphs of Polynomial Functions The degree of a polynomial function affects the shape of its graph. The graphs below show the general shapes of several polynomial functions. The graphs show the maximum number of times the graph of each type of polynomial may cross the x-axis. For example, a polynomial function of degree 4 may cross the x-axis a maximum of 4 times. Linear Function Quadratic Function Degree 1 Degree 2 Cubic Function Quartic Function Degree 3 Degree 4 Quintic Function Degree 5 Notice the general shapes of the graphs of odd degree polynomial functions and even degree polynomial functions. The degree and leading coefficient of a polynomial function affects the graph’s end behavior. End behavior is the direction of the graph to the far left and to the far right. The chart below summarizes the end behavior of a Polynomial Function. Degree Leading Coefficient End behavior of graph Even Positive Graph goes up to the far left and goes up to the far right. Even Negative Graph goes down to the far left and down to the far right. Odd Positive Graph goes down to the far left and up to the far right.
    [Show full text]
  • Fundamental Units and Regulators of an Infinite Family of Cyclic Quartic Function Fields
    J. Korean Math. Soc. 54 (2017), No. 2, pp. 417–426 https://doi.org/10.4134/JKMS.j160002 pISSN: 0304-9914 / eISSN: 2234-3008 FUNDAMENTAL UNITS AND REGULATORS OF AN INFINITE FAMILY OF CYCLIC QUARTIC FUNCTION FIELDS Jungyun Lee and Yoonjin Lee Abstract. We explicitly determine fundamental units and regulators of an infinite family of cyclic quartic function fields Lh of unit rank 3 with a parameter h in a polynomial ring Fq[t], where Fq is the finite field of order q with characteristic not equal to 2. This result resolves the second part of Lehmer’s project for the function field case. 1. Introduction Lecacheux [9, 10] and Darmon [3] obtain a family of cyclic quintic fields over Q, and Washington [22] obtains a family of cyclic quartic fields over Q by using coverings of modular curves. Lehmer’s project [13, 14] consists of two parts; one is finding families of cyclic extension fields, and the other is computing a system of fundamental units of the families. Washington [17, 22] computes a system of fundamental units and the regulators of cyclic quartic fields and cyclic quintic fields, which is the second part of Lehmer’s project. We are interested in working on the second part of Lehmer’s project for the families of function fields which are analogous to the type of the number field families produced by using modular curves given in [22]: that is, finding a system of fundamental units and regulators of families of cyclic extension fields over the rational function field Fq(t). In [11], we obtain the results for the quintic extension case.
    [Show full text]
  • Stabilities of Mixed Type Quintic-Sextic Functional Equations in Various Normed Spaces
    Malaya Journal of Matematik, Vol. 9, No. 1, 217-243, 2021 https://doi.org/10.26637/MJM0901/0038 Stabilities of mixed type Quintic-Sextic functional equations in various normed spaces John Micheal Rassias1, Elumalai Sathya2, Mohan Arunkumar 3* Abstract In this paper, we introduce ”Mixed Type Quintic - Sextic functional equations” and then provide their general solution, and prove generalized Ulam - Hyers stabilities in Banach spaces and Fuzzy normed spaces, by using both the direct Hyers - Ulam method and the alternative fixed point method. Keywords Quintic functional equation, sextic functional equation, mixed type quintic - sextic functional equation, generalized Ulam - Hyers stability, Banach space, Fuzzy Banach space, Hyers - Ulam method, alternative fixed point method. AMS Subject Classification 39B52, 32B72, 32B82. 1Pedagogical Department - Mathematics and Informatics, The National and Kapodistrian University of Athens,4, Agamemnonos Str., Aghia Paraskevi, Athens 15342, Greece. 2Department of Mathematics, Shanmuga Industries Arts and Science College, Tiruvannamalai - 606 603, TamilNadu, India. 3Department of Mathematics, Government Arts College, Tiruvannamalai - 606 603, TamilNadu, India. *Corresponding author: 1 [email protected]; 2 [email protected]; 3 [email protected] Article History: Received 11 December 2020; Accepted 24 January 2021 c 2021 MJM. Contents such problems the interested readers can refer the monographs of [1,4,5,8, 18, 22, 24–26, 33, 36, 37, 41, 43, 48]. 1 Introduction.......................................217 The general solution of Quintic and Sextic functional 2 General Solution..................................218 equations 3 Stability Results In Banach Space . 219 f (x + 3y) − 5 f (x + 2y) + 10 f (x + y) − 10 f (x) 3.1 Hyers - Ulam Method.................. 219 + 5 f (x − y) − f (x − 2y) = 120 f (y) (1.1) 3.2 Alternative Fixed Point Method..........
    [Show full text]
  • Polynomial Theorems
    COMPLEX ANALYSIS TOPIC IV: POLYNOMIAL THEOREMS PAUL L. BAILEY 1. Preliminaries 1.1. Basic Definitions. Definition 1. A polynomial with real coefficients is a function of the form n n−1 f(x) = anx + an−1x + ··· + a1x + a0; where ai 2 R for i = 0; : : : ; n, and an 6= 0 unless f(x) = 0. We call n the degree of f. We call the ai's the coefficients of f. We call a0 the constant coefficient of f, and set CC(f) = a0. We call an the leading coefficient of f, and set LC(f) = an. We say that f is monic if LC(f) = 1. The zero function is the polynomial of the form f(x) = 0. A constant function is a polynomial of degree zero, so it is of the form f(x) = c for some c 2 R. The graph of a constant function is a horizontal line. Constant polynomials may be viewed simply as real numbers. A linear function is a polynomial of degree one, so it is of the form f(x) = mx+b for some m; b 2 R with m 6= 0. The graph of such a function is a non-horizontal line. A quadratic function is a polynomial of degree two, of the form f(x) = ax2+bx+c for some a; b; c 2 R with a 6= 0. A cubic function is a polynomial of degree three. A quartic function is a polynomial of degree four. A quintic function is a polynomial of degree five. 1.2. Basic Facts. Let f and g be real valued functions of a real variable.
    [Show full text]
  • Locating Complex Roots of Quintic Polynomials Michael J
    The Mathematics Enthusiast Volume 15 Article 12 Number 3 Number 3 7-1-2018 Locating Complex Roots of Quintic Polynomials Michael J. Bosse William Bauldry Steven Otey Let us know how access to this document benefits ouy . Follow this and additional works at: https://scholarworks.umt.edu/tme Recommended Citation Bosse, Michael J.; Bauldry, William; and Otey, Steven (2018) "Locating Complex Roots of Quintic Polynomials," The Mathematics Enthusiast: Vol. 15 : No. 3 , Article 12. Available at: https://scholarworks.umt.edu/tme/vol15/iss3/12 This Article is brought to you for free and open access by ScholarWorks at University of Montana. It has been accepted for inclusion in The Mathematics Enthusiast by an authorized editor of ScholarWorks at University of Montana. For more information, please contact [email protected]. TME, vol. 15, no.3, p. 529 Locating Complex Roots of Quintic Polynomials Michael J. Bossé1, William Bauldry, Steven Otey Department of Mathematical Sciences Appalachian State University, Boone NC Abstract: Since there are no general solutions to polynomials of degree higher than four, high school and college students only infrequently investigate quintic polynomials. Additionally, although students commonly investigate real roots of polynomials, only infrequently are complex roots – and, more particularly, the location of complex roots – investigated. This paper considers features of graphs of quintic polynomials and uses analytic constructions to locate the functions’ complex roots. Throughout, hyperlinked dynamic applets are provided for the student reader to experientially participate in the paper. This paper is an extension to other investigations regarding locating complex roots (Bauldry, Bossé, & Otey, 2017). Keywords: Quartic, Quintic, Polynomials, Complex Roots Most often, when high school or college students investigate polynomials, they begin with algebraic functions that they are asked to either factor or graph.
    [Show full text]
  • Answers, Solution Outlines and Comments to Exercises
    A Answers, Solution Outlines and Comments to Exercises Chapter 1 Preliminary Test (page 3) 1. p7. [c2 = a2 + b2 2ab cos C.] (5 marks) − x y dy 2. 4=3 + 16 = 1. [Verify that the point is on the curve. Find slope dx = 12 (at that point) and− the tangent y + 8 = 12(x + 2). (5 marks) Rearrange the equation to get it in intercept form, or solve y = 0 for x-intercept and x = 0 for y-intercept.] (5 marks) 3. One. [Show that g0(t) < 0 t R, hence g is strictly decreasing. Show existence. Show uniqueness.] 8 2 (5 marks) Comment: Graphical solution is also acceptable, but arguments must be rigorous. p 3 2π Rh p 2 2 p 4. 4π(9 2 6) or 16:4π or 51.54 cm . [V = 0 0 2 R r rdrdθ, R = 3; Rh = 3. Sketc−h domain. − (5 marks) R R V = 4π Rh pR2 r2 rdr, substitute R2 r2 = t2. (5 marks) 0 − − pR2 R2 EvaluateR integral V = 4π − h t2dt.] (5 marks) − R 5. (a) (2,1,8). [Consider p~ Rq~ = ~s ~r.] (5 marks) QP~− QR~ − (b) 3=5. [cos Q = · .] (5 marks) QP~ QR~ k k k k (c) p9 (j + 2k). [Vector projection = (QP~ QR^ )QR^ .] (5 marks) 5 · (d) 6p6 square units. [Vector area = QP~ QR~ .] (5 marks) (e) 7x + 2y z = 8. × [Take normal− n in the direction of vector area and n (x q).] (5 marks) Comment: Parametric equation q + α(p q) + β(r· q−) is also acceptable. (f) 14, 4, 2 on yz, xz and xy planes.
    [Show full text]
  • Trajectory Planning for the Five Degree of Freedom Feeding Robot Using Septic and Nonic Functions
    International Journal of Mechanical Engineering and Robotics Research Vol. 9, No. 7, July 2020 Trajectory Planning for the Five Degree of Freedom Feeding Robot Using Septic and Nonic Functions Priyam A. Parikh Mechanical Engineering Department, Nimra University, Ahmedabad, India Email: [email protected] Reena Trivedi and Jatin Dave Email: { reena.trivedi, jatin.dave}@nirmauni.ac.in Abstract— In the present research work discusses about Instead of planning the trajectory using Cartesian scheme, trajectory planning of five degrees of freedom serial it is better to get the start point and end point of each joint manipulator using higher order polynomials. This robotic [2]. After getting the joint angles from the operational arm is used to feed semi-liquid food to the physically space, trajectory planning can be done using joint space challenged people having fixed seating arrangement. It is scheme. However trajectory planning in the Cartesian essential to plan a smooth trajectory for proper delivery of food, without wasting it. Trajectory planning can be done in space allows accounting for the presence of any constraint the joint space as well as in the cartesian space. It is difficult along the path of the end-effector, but singular to design trajectory in Cartesian scheme due to configuration and trajectory planning can’t be done with non-existence of the Jacobian matrix. In the present research operational space [3]. In the case of inverse kinematics no work, trajectory planning is done using joint space scheme. joint angle can be computed due to non-existence of the The joint space scheme offers lower and higher order inverse of the Jacobian matrix.
    [Show full text]
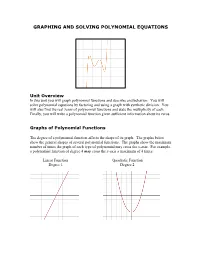
  • Graphing and Solving Polynomial Equations
    GRAPHING AND SOLVING POLYNOMIAL EQUATIONS Unit Overview In this unit you will graph polynomial functions and describe end behavior. You will solve polynomial equations by factoring and using a graph with synthetic division. You will also find the real zeros of polynomial functions and state the multiplicity of each. Finally, you will write a polynomial function given sufficient information about its zeros. Graphs of Polynomial Functions The degree of a polynomial function affects the shape of its graph. The graphs below show the general shapes of several polynomial functions. The graphs show the maximum number of times the graph of each type of polynomial may cross the x-axis. For example, a polynomial function of degree 4 may cross the x-axis a maximum of 4 times. Linear Function Quadratic Function Degree 1 Degree 2 Cubic Function Quartic Function Degree 3 Degree 4 Quintic Function Degree 5 Notice the general shapes of the graphs of odd degree polynomial functions and even degree polynomial functions. The degree and leading coefficient of a polynomial function affects the graph’s end behavior. End behavior is the direction of the graph to the far left and to the far right. The chart below summarizes the end behavior of a Polynomial Function. Degree Leading Coefficient End behavior of graph Even Positive Graph goes up to the far left and goes up to the far right. Even Negative Graph goes down to the far left and down to the far right. Odd Positive Graph goes down to the far left and up to the far right.
    [Show full text]
  • Linear and Polynomial Functions
    Linear and Polynomial Functions Math 130 - Essentials of Calculus 11 September 2019 Math 130 - Essentials of Calculus Linear and Polynomial Functions 11 September 2019 1 / 12 Intuitively, rise change in y slope = = : run change in x More concretely, if a line passes though the points (x1; y1) and (x2; y2), then the slope of the line is given by y − y ∆y m = 2 1 = : x2 − x1 ∆x Given the slope of a line, m, and a point it passes though (x1; y1), an equation for the line is y − y1 = m(x − x1): Section 1.3 - Linear Models and Rates of Change Reminder: Slope of a Line The slope of a line is a measure of its “steepness.” Positive indicating upward, negative indicating downward, and the greater the absolute value, the steeper the line. Math 130 - Essentials of Calculus Linear and Polynomial Functions 11 September 2019 2 / 12 More concretely, if a line passes though the points (x1; y1) and (x2; y2), then the slope of the line is given by y − y ∆y m = 2 1 = : x2 − x1 ∆x Given the slope of a line, m, and a point it passes though (x1; y1), an equation for the line is y − y1 = m(x − x1): Section 1.3 - Linear Models and Rates of Change Reminder: Slope of a Line The slope of a line is a measure of its “steepness.” Positive indicating upward, negative indicating downward, and the greater the absolute value, the steeper the line. Intuitively, rise change in y slope = = : run change in x Math 130 - Essentials of Calculus Linear and Polynomial Functions 11 September 2019 2 / 12 ∆y = : ∆x Given the slope of a line, m, and a point it passes though (x1; y1), an equation for the line is y − y1 = m(x − x1): Section 1.3 - Linear Models and Rates of Change Reminder: Slope of a Line The slope of a line is a measure of its “steepness.” Positive indicating upward, negative indicating downward, and the greater the absolute value, the steeper the line.
    [Show full text]
  • Polynomial and Power Functions N N 1 2 F (X) = Anx + an 1X − +
    polynomial functions polynomial functions Polynomial Functions MHF4U: Advanced Functions You have seen polynomial functions in previous classes. Common polynomial functions include constant, linear, quadratic and cubic functions. A polynomial function has the form Polynomial and Power Functions n n 1 2 f (x) = anx + an 1x − + ... + a2x + a1x + a0 − J. Garvin where n is a whole number and ak is a coefficient. The degree of the polynomial is the exponent of the greatest power. The leading coefficient is an, and the constant term is a0. J. Garvin— Polynomial and Power Functions Slide 1/17 Slide 2/17 polynomial functions polynomial functions Polynomial Functions Classifying Polynomial Functions Polynomial functions of degree 2 or greater can be drawn Example using a series of smooth, connected curves, as in the example Is the function f (x) = 3x5 x2 + 4x 1 a polynomial − − below. function? f (x) is a polynomial function. It has degree 5, a leading coefficient of 3, and a constant term of 1. − Note that there are no x3 and x4 terms. This is because the coeffients on these terms, a3 and a4, are both zero. J. Garvin— Polynomial and Power Functions J. Garvin— Polynomial and Power Functions Slide 3/17 Slide 4/17 polynomial functions polynomial functions Classifying Polynomial Functions Classifying Polynomial Functions Example Example Is the function f (x) = 2x 5 a polynomial function? 1 − Is the function f (x) = 3x 2 a polynomial function? f (x) is not a polynomial function, but an exponential f (x) is not a polynomial function, but a radical function. function. The exponents in a polynomial function are always whole Don’t be confused when the variable is the exponent.
    [Show full text]
  • A5-1 Polynomial Functions
    M1 Maths A5-1 Polynomial Functions general form and graph shape equation solution methods applications Summary Learn Solve Revise Answers Summary A polynomial function is made of a number of terms. Each term consists of a whole- number power of the independent variable multiplied by a real number. The graph of a polynomial consists of a number of straighter sections called arms separated by more curved sections called elbows. The number of arms is less than or equal to the degree of the polynomial (the highest power of the independent variable). You already know how to solve polynomial equations up to degree 2. In general, higher-degree equations can only be readily solved by graphing. Linear and quadratic functions are the most commonly used polynomials, but higher- degree polynomials have applications in volume, trigonometry etc. Learn General Form You know a bit about linear and quadratic functions. But these are part of a larger family called polynomial functions. Constant functions are of the form y = c Linear functions are of the form y = mx + c Quadratic functions are of the form y = ax2 + bx + c This sequence can be continued . Cubic functions are of the form y = ax3 + bx2 + cx + d Quartic functions are of the form y = ax4 + bx3 + cx2 + dx + e You will probably notice a pattern here. The pattern continues . M1Maths.com A5-1 Polynomial Functions Page 1 Quintic functions are of the form y = ax5 + bx4 + cx3 + dx2 + ex + f Sexual functions are of the form y = ax6 + bx5 + cx4 + dx3 + ex2 + fx + g [Of course sexual function has a completely different meaning in common English – be careful not to confuse the two.] Septic functions are of the form y = ax7 + bx6 + cx5 + dx4 + ex3 + fx2 + gx + h And so on ad infinitum .
    [Show full text]
  • Analyzing Structure
    Integrated Math III Textbook Table of Contents Analyzing Structure 1 Pacing: 42 Days Topic 1: Exploring and Analyzing Patterns Exploring and Analyzing Patterns begins with opportunities for students to analyze and describe various patterns. Questions ask students to represent algebraic expressions in different forms and use algebra and graphs to determine whether they are equivalent. They identify linear, exponential, and quadratic functions using multiple representations. The three forms of a quadratic equation are reviewed, and students learn to write quadratic equations given key points before using a system to write a quadratic equation given any three points. Finally, students recall how to solve quadratic equations. Standards: A.SSE.1a, A.SSE.1b, A.SSE.2, A.APR.1, A.CED.1, A.CED.2, A.REI.4, A.REI.4a, A.REI.4b, A.REI.7, F.IF.4, F.IF.8, F.IF.9, F.BF.1a Pacing: 17 Days Lesson Title / Subtitle Standards Pacing* Lesson Summary Essential Ideas This lesson revisits the three scenarios from the previous lesson. Students will write equivalent algebraic expressions for the tile pattern of a square floor to determine the number of new tiles that must be added to create the next square tile design. They then show that the expressions are equivalent using the distributive property and combining Patterns: They’re like terms. In the second activity, equivalent expressions • Sequences are used to show observable patterns. are written to represent the exponential situation for Grrrrrowing! F.IF.8 1 • Patterns are used to solve problems. 1 keeping secrets. Students then prove the expressions to • Functions can be used to describe patterns.
    [Show full text]