DOCSLIB.ORG

Geometry Tutor Worksheet 16 Area of Prisms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometry Tutor Worksheet 16 Area of Prisms Geometry Tutor Worksheet 16 Area of Prisms 1 © MathTutorDVD.com Geometry Tutor - Worksheet 16 – Area of Prisms 1. What is the total surface area of a rectangular prism whose length is 9 m, width is 5 m, and height is 12 m? 2. What is the total surface area of a rectangular prism whose length is 4.6 cm, width is 3.8 cm, and height is 1.4 cm? 3. What is the width of a rectangular prism whose total surface area is 184 m2 whose length is 5 m, and height is 4 m? 2 © MathTutorDVD.com 4. What is the height of a rectangular prism whose total surface area is 318 cm2 whose length is 6 cm, and width is 9 cm? 5. What is the total surface area of this rectangular prism? 6. What is the total surface area of this cubic prism? 3 © MathTutorDVD.com 7. What is the total surface area of this rectangular prism if 푈푉 = 9 mm, 푆푌 = 15 mm, and 푇푊 = 6 mm? 8. What is the total surface area of this triangular prism? 4 © MathTutorDVD.com 9. What is the total surface area of this rectangular prism? 10. What is the total surface area of this rectangular prism? 5 © MathTutorDVD.com 11. What is the total surface area of this rectangular prism if 퐴퐵 = 7 cm, 퐵퐶 = 11 cm, and 퐶퐺 = 14 cm? 12. What is the total surface area of this triangular prism? 6 © MathTutorDVD.com 13. What is the total surface area of this heptagonal prism if the area of the base is 140 mm2? 14. What is the total surface area of this triangular prism? 7 © MathTutorDVD.com 15. What is the total surface area of this regular pentagonal prism if the area of the base is 30 hm2? 8 © MathTutorDVD.com Answers - Geometry Tutor - Worksheet 16 – Area of Prisms 1. What is the total surface area of a rectangular prism whose length is 9 m, width is 5 m, and height is 12 m? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. Therefore, 퐴 = 2(9 m ∙ 12 m + 9 m ∙ 5 m + 12 m ∙ 5 m) 퐴 = 2(9 ∙ 12 + 9 ∙ 5 + 12 ∙ 5) m2 퐴 = 2(213 ) m2 퐴 = 426 m2 Answer: 426 m2 2. What is the total surface area of a rectangular prism whose length is 4.6 cm, width is 3.8 cm, and height is 1.4 cm? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. Therefore, 퐴 = 2(4.6 cm ∙ 1.4 cm + 4.6 cm ∙ 3.8 cm + 1.4 cm ∙ 3.8 cm) 퐴 = 2(4.6 ∙ 1.4 + 4.6 ∙ 3.8 + 1.4 ∙ 3.8) cm2 퐴 = 2(29.24 ) cm2 퐴 = 58.48 cm2 Answer: 58.48 cm2 9 © MathTutorDVD.com 3. What is the width of a rectangular prism whose total surface area is 184 m2 whose length is 5 m, and height is 4 m? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. Therefore, 184 m2 = 2(5 m ∙ 4 m + 5 m ∙ 푥 m + 4 m ∙ 푥 m) 184 m2 = 2(5 ∙ 4 + 5 ∙ 푥 + 4 ∙ 푥) m2 184 = 2(20 + 9푥 ) 92 = 20 + 9푥 72 = 9푥 푥 = 8 Answer: 8 m 4. What is the height of a rectangular prism whose total surface area is 318 cm2 whose length is 6 cm, and width is 9 cm? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. Therefore, 2 318 cm = 2(6 cm ∙ 푥 cm + 6 cm ∙ 9 cm + 푥 cm ∙ 9 cm) 2 2 318 cm = 2(6 ∙ 푥 + 6 ∙ 9 + 푥 ∙ 9) cm 318 = 2(15푥 + 54) 159 = 15푥 + 54 105 = 15푥 푥 = 7 10 © MathTutorDVD.com Answer: 7 cm 5. What is the total surface area of this rectangular prism? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. Therefore, 퐴 = 2(7 m ∙ 8 m + 7 m ∙ 6 m + 8 m ∙ 6 m) 퐴 = 2(7 ∙ 8 + 7 ∙ 6 + 8 ∙ 6) m2 퐴 = 2(146) m2 퐴 = 292 m2 Answer: 292 m2 11 © MathTutorDVD.com 6. What is the total surface area of this cubic prism? The formula for calculating the total surface area of a cubic prism is 퐴 = 6푙2 where 퐴 is the area, 푙 is the length of the sides. Therefore, 퐴 = 6 ∙ (9 cm)2 퐴 = 6(81) cm2 퐴 = 486 cm2 Answer: 486 cm2 7. What is the total surface area of this rectangular prism if 푈푉 = 9 mm, 푆푌 = 15 mm, and 푇푊 = 6 mm? The formula for calculating the total surface area of a rectangular prism is 12 © MathTutorDVD.com 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. The question gives the length, width, and height. Therefore, 퐴 = 2(15 mm ∙ 6 mm + 15 mm ∙ 9 mm + 6 mm ∙ 9 mm) 퐴 = 2(15 ∙ 6 + 15 ∙ 9 + 6 ∙ 9) mm2 퐴 = 2(279) mm2 퐴 = 558 mm2 Answer: 558 mm2 8. What is the total surface area of this triangular prism? Calculate the total surface area of a triangular prism by calculating the area of the bases and the lateral surface areas and add the areas. The formula for areas of the bases is twice the area of a triangle. Therefore, the 1 formula is 퐵 = 2 ( 푏ℎ) where 퐵 is the area of the bases, 푏 is the length of the 2 base of the triangles, and ℎ is the height of the triangles. Therefore, 1 퐵 = 2 ( ∙ 24 mm ∙ 5 mm) 2 1 퐵 = 2 ( ∙ 24 ∙ 5) mm2 2 13 © MathTutorDVD.com 퐵 = 2(60) mm2 퐵 = 120 mm2 Now calculate the areas of the lateral faces which are all rectangles and add all of the areas together. 퐴 = 120 mm2 + 28 mm ∙ 24 mm + 28 mm ∙ 13 mm + 28 mm ∙ 13 mm 퐴 = 120 mm2 + 28 ∙ 24 mm2 + 28 ∙ 13 mm2 + 28 ∙ 13 mm2 퐴 = 120 mm2 + 672 mm2 + 364 mm2 + 364 mm2 퐴 = 1520 mm2 Answer: 1520 mm2 9. What is the total surface area of this rectangular prism? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. The question gives the length, width, and height. Therefore, 퐴 = 2(6 km ∙ 7 km + 6 km ∙ 6 km + 7 km ∙ 6 km) 2 퐴 = 2(6 ∙ 7 + 6 ∙ 6 + 7 ∙ 6) km 2 퐴 = 2(120) km 14 © MathTutorDVD.com 퐴 = 240 km2 Answer: 240 km2 10. What is the total surface area of this rectangular prism? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. Therefore, 퐴 = 2(3.8 cm ∙ 4.1 cm + 3.8 cm ∙ 3.6 cm + 4.1 cm ∙ 3.6 cm) 퐴 = 2(3.8 ∙ 4.1 + 3.8 ∙ 3.6 + 4.1 ∙ 3.6) cm2 퐴 = 2(44.02 ) cm2 퐴 = 88.04 cm2 Answer: 88.04 cm2 15 © MathTutorDVD.com 11. What is the total surface area of this rectangular prism if 퐴퐵 = 7 cm, 퐵퐶 = 11 cm, and 퐶퐺 = 14 cm? The formula for calculating the total surface area of a rectangular prism is 퐴 = 2(푙ℎ + 푙푤 + ℎ푤) where 퐴 is the area, 푙 is the length, ℎ is the height, and 푤 is the width. The question gives the length, width, and height. Therefore, 퐴 = 2(11 cm ∙ 14 cm + 11 cm ∙ 7 cm + 14 cm ∙ 7 cm) 퐴 = 2(11 ∙ 14 + 11 ∙ 7 + 14 ∙ 7) cm2 퐴 = 2(329) cm2 퐴 = 658 cm2 Answer: 658 cm2 16 © MathTutorDVD.com 12. What is the total surface area of this triangular prism? Calculate the total surface area of a triangular prism by calculating the area of the bases and the lateral surface areas and add the areas. The formula for areas of the bases is twice the area of a triangle. Therefore, the 1 formula is 퐵 = 2 ( 푏ℎ) where 퐵 is the area of the bases, 푏 is the length of the 2 base of the triangles, and ℎ is the height of the triangles. The triangles are right triangles, so the legs are the base and the height. Therefore, 1 퐵 = 2 ( ∙ 6 m ∙ 6 m) 2 1 퐵 = 2 ( ∙ 6 ∙ 8) m2 2 퐵 = 2(24) m2 퐵 = 48 m2 Now calculate the areas of the lateral faces which are all rectangles and add all of the areas together. Notice again that the triangular bases are right triangles, so using the Pythagorean Theorem formula, we calculate that the length of the hypotenuse is 10 cm.
Load more

Recommended publications
  • Year 6 – Wednesday 24Th June 2020 – Maths
    1 Year 6 – Wednesday 24th June 2020 – Maths Can I identify 3D shapes that have pairs of parallel or perpendicular edges? Parallel – edges that have the same distance continuously between them – parallel edges never meet. Perpendicular – when two edges or faces meet and create a 90o angle. 1 4. 7. 10. 2 5. 8. 11. 3. 6. 9. 12. C1 – Using the shapes above: 1. Name and sort the shapes into: a. Pyramids b. Prisms 2. Draw a table to identify how many faces, edges and vertices each shape has. 3. Write your own geometric definition: a. Prism b. pyramid 4. Which shape is the odd one out? Explain why. C2 – Using the shapes above; 1. Which of the shapes have pairs of parallel edges in: a. All their faces? b. More than one half of the faces? c. One face only? 2. The following shapes have pairs of perpendicular edges. Identify the faces they are in: 2 a. A cube b. A square based pyramid c. A triangular prism d. A cuboid 3. Which shape with straight edges has no perpendicular edges? 4. Which shape has perpendicular edges in the shape but not in any face? C3 – Using the above shapes: 1. How many faces have pairs of parallel edges in: a. A hexagonal pyramid? b. A decagonal (10-sided) based prism? c. A heptagonal based prism? d. Which shape has no face with parallel edges but has parallel edges in the shape? 2. How many faces have perpendicular edges in: a. A pentagonal pyramid b. A hexagonal pyramid c.
    [Show full text]
  • Geometry Worksheet -- Classifying Prisms and Pyramids
    Classifying Prisms and Pyramids (A) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (A) Answers Name each figure based on the shape of its base. heptagonal prism square prism hexagonal prism heptagonal pyramid hexagonal prism pentagonal prism rectangular prism octagonal pyramid Math-Drills.com Classifying Prisms and Pyramids (B) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (B) Answers Name each figure based on the shape of its base. square prism heptagonal pyramid pentagonal pyramid triangular prism square pyramid rectangular prism triangular prism rectangular pyramid Math-Drills.com Classifying Prisms and Pyramids (C) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (C) Answers Name each figure based on the shape of its base. pentagonal pyramid square prism, cube octagonal prism heptagonal pyramid heptagonal pyramid rectangular pyramid rectangular prism pentagonal prism Math-Drills.com Classifying Prisms and Pyramids (D) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (D) Answers Name each figure based on the shape of its base. square pyramid heptagonal prism hexagonal prism heptagonal pyramid square prism, cube square pyramid triangular prism octagonal prism Math-Drills.com Classifying Prisms and Pyramids (E) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (E) Answers Name each figure based on the shape of its base. square prism octagonal prism rectangular prism octagonal prism pentagonal pyramid hexagonal prism pentagonal prism heptagonal pyramid Math-Drills.com Classifying Prisms and Pyramids (F) Name each figure based on the shape of its base.
    [Show full text]
  • Geometry Tutor Worksheet 17 Volume of Prisms and Pyramids
    Geometry Tutor Worksheet 17 Volume of Prisms and Pyramids 1 © MathTutorDVD.com Geometry Tutor - Worksheet 17 – Volume of Prisms and Pyramids 1. What is the volume of a rectangular prism whose length is 9 m, width is 5 m, and height is 12 m? 2. What is the volume of a rectangular prism whose length is 4.6 cm, width is 3.8 cm, and height is 1.4 cm? 3. What is the width of a rectangular prism whose volume is 216 m3 whose length is 6 m, and height is 9 m? 2 © MathTutorDVD.com 4. What is the height of a rectangular prism whose volume is 672 cm3 whose length is 12 cm, and width is 7 cm? 5. What is the volume of this rectangular prism? 6. What is the volume of this cubic prism? 3 © MathTutorDVD.com 7. What is the volume of this rectangular prism if 푈푉 = 9 mm, 푆푌 = 15 mm, and 푇푊 = 6 mm? 8. What is the volume of this triangular prism? 4 © MathTutorDVD.com 9. What is the volume of this rectangular prism? 10. What is the volume of this rectangular prism? 5 © MathTutorDVD.com 11. What is the volume of this rectangular prism if 퐴퐵 = 7 cm, 퐵퐶 = 11 cm, and 퐶퐺 = 14 cm? 12. What is the volume of this triangular prism? 6 © MathTutorDVD.com 13. What is the volume of this heptagonal prism if the area of the base is 140 mm2? 14. What is the volume of this triangular prism? 7 © MathTutorDVD.com 15. What is the volume of this regular pentagonal prism if the area of the base is 30 hm2? 16.
    [Show full text]
  • 7Th Grade | Unit 10
    MATH STUDENT BOOK 7th Grade | Unit 10 804 N. 2nd Ave. E. Rock Rapids, IA 51246-1759 800-622-3070 www.aop.com Unit 10 | Surface Area and Volume Math 710 Surface Area and Volume Introduction |3 1. Solids 5 Classifying and Identifying Solids |5 Nets |12 Surface Area and Volume |18 Self Test 1: Solids |25 2. Prisms 29 Surface Area of Rectangular Prisms |29 Volume of Rectangular Prisms |35 Surface Area of Triangular Prisms |40 Volume of Triangular Prisms |47 Self Test 2: Prisms |52 3. Cylinders 55 Surface Area of Cylinders |55 Volume of Cylinders |60 Dimension Changes |65 Self Test 3: Cylinders |72 4. Review 77 LIFEPAC Test is located in the center of the booklet. Please remove before starting the unit. Section 1 |1 Surface Area and Volume | Unit 10 Author: Glynlyon Staff Editors: Alan Christopherson, M.S. Michelle Chittam Westover Studios Design Team: Phillip Pettet, Creative Lead Teresa Davis, DTP Lead Nick Castro Andi Graham Jerry Wingo 804 N. 2nd Ave. E. Rock Rapids, IA 51246-1759 © MMXIV by Alpha Omega Publications, a division of Glynlyon, Inc. All rights reserved. LIFEPAC is a registered trademark of Alpha Omega Publications, Inc. All trademarks and/or service marks referenced in this material are the property of their respective owners. Alpha Omega Publications, Inc. makes no claim of ownership to any trademarks and/ or service marks other than their own and their affiliates, and makes no claim of affiliation to any companies whose trademarks may be listed in this material, other than their own. Some clip art images used in this curriculum are from Corel Corporation, 1600 Carling Avenue, Ottawa, Ontario, Canada K1Z 8R7.
    [Show full text]
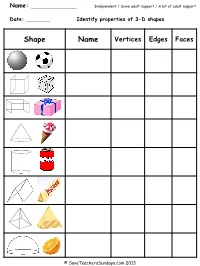
  • Name: Date: Identify Properties of 3-D Shapes
    Name: Independent / Some adult support / A lot of adult support Date: Identify properties of 3-D shapes Shape Name Vertices Edges Faces © SaveTeachersSundays.com 2013 Answers Shape Name Vertices Edges Faces Sphere 0 0 1 Cube 8 12 6 Cuboid 8 12 6 Cone 0 / 1 1 2 Cylinder 0 2 3 Prism 6 9 5 Pyramid 5 8 5 Hemisphere 0 1 2 © SaveTeachersSundays.com 2013 Name: Independent / Some adult support / A lot of adult support Date: Identify properties of 3-D shapes Shape Name Vertices Edges Faces © SaveTeachersSundays.com 2013 Name: Independent / Some adult support / A lot of adult support Date: Identify properties of 3-D shapes Shape Name Vertices Edges Faces based pyramid based pyramid based pyramid based pyramid prism prism prism © SaveTeachersSundays.com 2013 Answers Shape Name Vertices Edges Faces Triangular-based pyramid 4 6 4 Square-based pyramid 5 8 5 Pentagonal-based pyramid 6 10 6 Hexagonal-based pyramid 7 12 7 Triangular prism 6 9 5 Pentagonal prism 10 15 7 Hexagonal prism 12 18 8 © SaveTeachersSundays.com 2013 Solve 3-D shape problems The view you have of each of these 3-D shapes means that you can only see one of each of their faces. For each question make a list of the 3-D shapes that it could be Sphere Cube Cuboid Cone Cylinder Hemisphere - based pyramid prism 1) 2) 3) 4) 5) 6) 7) 8) © SaveTeachersSundays.com 2013 Answers Sphere Cube Cuboid Cone Cylinder Hemisphere - based pyramid prism 1) Cube, cuboid and square-based pyramid 2) Cone, hemisphere and cylinder 3) Triangular prism and triangular-based pyramid 4) Cuboid (not all of the other prisms because you would always be able to see part of another face) 5) Hexagonal prism and hexagonal-based pyramid 6) Pentagonal-based pyramid and pentagonal prism 7) Octagonal-based pyramid and Octagonal prism 8) Heptagonal-based pyramid and heptagonal prism © SaveTeachersSundays.com 2013 .
    [Show full text]
  • Balance Edge-Magic Graphs of Prism and Anti Prism Graphs
    Middle-East Journal of Scientific Research 25 (2): 393-401, 2017 ISSN 1990-9233 © IDOSI Publications, 2017 DOI: 10.5829/idosi.mejsr.2017.393.401 Weak Q(a) Balance Edge-Magic Graphs of Prism and Anti prism graphs S. Vimala Department of Mathematics, Mother Teresa Women’s University, Kodaikanal, TN, India Abstract: A graph G is a (p,q) graph in which the edges are labeled by 1,2,3,…,q so that the vertex sum are constant, mod p, than G is called an edge-magic graph. A (p,q)-graph G in which the edges are labeled by Q(a) so that vertex sums mod p is constant, is called Q(a)-Balance Edge-Magic Graph (In short Q(a)-BEM). In this article defines weak Q(a) balance edge-magic of Triangular prism graphs, Cubical prism graphs, Pentagonal prism graphs, Hexagonal prism graphs, Heptagonal prism graph, Cube Antiprism graph, Square Antiprism graph, Antiprism graph. Key words: Magic Edge magic Q(a) balance edge magic Prism Antiprism INTRODUCTION Magic Graphs(BEM) by Sin-Min Lee and Thomas Wong, Sheng – Ping Bill Lo [13] verified for regular graph, A graph labeling is an assignment of integers to the pendent vertices, friendship graph, complete graph, vertices or edges or both subject to certain conditions. complete bipartite graph, fan graph and wheel graphs. In Number theory gives more conjunctures to find 2009, Q(a) Balance Edge-Magic extended the results to labelling graphs. In 1963, Sedlá ek introduced magic some conjuncture by Ping-Tsai Chung, Sin-Min Lee [10]. labelling. This Labeled graphs are useful to form family of In [14, 15] extended some conjuncture results and some Mathematical Models from a broad range of applications.
    [Show full text]
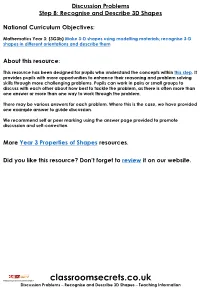
  • Year 3 Recognise and Describe 3D Shapes Discussion Problems
    Discussion Problems Step 8: Recognise and Describe 3D Shapes National Curriculum Objectives: Mathematics Year 3: (3G3b) Make 3-D shapes using modelling materials; recognise 3-D shapes in different orientations and describe them About this resource: This resource has been designed for pupils who understand the concepts within this step. It provides pupils with more opportunities to enhance their reasoning and problem solving skills through more challenging problems. Pupils can work in pairs or small groups to discuss with each other about how best to tackle the problem, as there is often more than one answer or more than one way to work through the problem. There may be various answers for each problem. Where this is the case, we have provided one example answer to guide discussion. We recommend self or peer marking using the answer page provided to promote discussion and self-correction. More Year 3 Properties of Shapes resources. Did you like this resource? Don’t forget to review it on our website. © Classroom Secrets Limited 2019 classroomsecrets.co.uk Discussion Problems – Recognise and Describe 3D Shapes – Teaching Information Recognise and Describe 3D Shapes 1. Complete the Magic Square so that the combined total of faces or surfaces in each row, column or diagonal is the same. You can only use each shape once. pentagonal cone heptagonal square prism Prism based pyramid sphere triangular cube based pyramid cylinder hexagonal prism DP 2. Explore combinations of 3D shapes which have a total of 20 vertices. You cannot use the same shape more than once in any one combination.
    [Show full text]
  • CHAPTER 12 Surface Area and Volume Chapter Outline
    www.ck12.org Chapter 12. Surface Area and Volume CHAPTER 12 Surface Area and Volume Chapter Outline 12.1 EXPLORING SOLIDS 12.2 SURFACE AREA OF PRISMS AND CYLINDERS 12.3 SURFACE AREA OF PYRAMIDS AND CONES 12.4 VOLUME OF PRISMS AND CYLINDERS 12.5 VOLUME OF PYRAMIDS AND CONES 12.6 SURFACE AREA AND VOLUME OF SPHERES 12.7 EXPLORING SIMILAR SOLIDS 12.8 CHAPTER 12 REVIEW In this chapter we extend what we know about two-dimensional figures to three-dimensional shapes. First, we will determine the parts and different types of 3D shapes. Then, we will find the surface area and volume of prisms, cylinders, pyramids, cones, and spheres. Lastly, we will expand what we know about similar shapes and their areas to similar solids and their volumes. 677 12.1. Exploring Solids www.ck12.org 12.1 Exploring Solids Learning Objectives • Identify different types of solids and their parts. • Use Euler’s formula to solve problems. • Draw and identify different views of solids. • Draw and identify nets. Review Queue 1. Draw an octagon and identify the edges and vertices of the octagon. How many of each are there? 2. Find the area of a square with 5 cm sides. 3. Find the area of an equilateral triangle with 10 in sides. 4. Draw the following polygons. (a) A convex pentagon. (b) A concave nonagon. Know What? Until now, only two-dimensional, or flat, shapes have been studies. This chapter will expand the studies to 3D. Copy the equilateral triangle to the right onto a piece of paper and cut it out.
    [Show full text]
  • Decagonal Prism. Solution: Faces Vertices Edges
    CHAPTER – 17 VISUALISING SOLID SHAPES Exercise 17.1 1. Match the objects with their shapes: Picture (object) Shape A tent A triangular field adjoining a square field. A tin A hemispherical shell. © PRAADIS EDUCATION A bowl DO NOTTwo COPYrectangular cross paths inside a rectangular park. An A hemisphere surmounted on agricultur a cone. al field A groove A circular path around a circular ground. A toy A cylindrical shell. A circular A cone surmounted on a park cylinder. © PRAADIS A cross A cone taken out of a cylinder. path EDUCATION DO NOT COPY Solution: (i) A tent – (g) A cone surmounted on a cylinder. (ii) A tin – (f) A cylindrical shell. (iii) A bowl – (b) A hemispherical shell. (iv) An agricultural field – (a) A triangular field adjoining a square field. (v) A groove – (h) A cone taken out of a cylinder. (vi) A toy – (d) A hemisphere surmounted on a cone. (vii) A circular park – (e) A circular path around a circular ground. (viii) A cross path – (c) Two rectangular© crossPRAADIS paths inside a rectangular park. 2. For each of the given solid, the two views are given. Match for each solid the correspondingEDUCATION front and top views. DO NOT COPY © PRAADIS EDUCATION DO NOT COPY Solution: Object Front View Top View A bottle (iii) (y) A funnel (i) (v) A flash (ii) (u) A shuttle cock (vi) (x) A box (iv) (z) A weight (v) (w) 3. For the given solid, identify the front, side and top views and write it in the space provided. © PRAADIS EDUCATION DO NOT COPY Solution: 4.
    [Show full text]
  • Paper Models of Prisms Gijs Korthals Altes
    Paper Models of Prisms Gijs Korthals Altes www.korthalsaltes.com Copyright © 2009 Gijs Korthals Altes All rights reserved. It's permitted to make copies for non-commercial purposes only. email: [email protected] www.korthalsaltes.com Triangular Prism Triangular Prism Rectangular Prism Faces: 5 Edges: 9 Vertices: 6 Faces: 5 Edges: 9 Vertices: 6 Faces: 6 Edges: 12 Vertices: 8 Pentagonal Prism Hexagonal Prism Heptagonal Prism Faces: 7 Edges: 15 Vertices: 10 Faces: 8 Edges: 18 Vertices: 12 Faces: 9 Edges: 21 Vertices: 14 Octagonal Prism Enneagonal Prism Decagonal Prism Faces: 10 Edges: 24 Vertices: 16 Faces: 11 Edges: 27 Vertices: 18 Faces: 12 Edges: 30 Vertices: 20 Copyright © 1998 - 2009 Gijs Korthals Altes www.korthalsaltes.com Hendecagonal Prism Dodecagonal Prism Faces: 13 Edges: 33 Vertices: 22 Faces: 14 Edges: 36 Vertices: 24 Prism: A general prism is a polyhedron possessing two congruent polygonal faces and with all remaining faces parallelograms. A right prism is a prism in which the top and bottom polygons lie on top of each other so that the vertical polygons connecting their sides are not only parallelograms, but rectangles. A prism that is not a right prism is known as an oblique prism. If, in addition, the upper and lower bases are rectangles, then the prism is known as a cuboid. A polyhedron (plural: polyhedra) is a three - dimensional figure made up of sides called faces, each face being a polygon. A polygon is a two dimensional figure made up of line segments called edges, that are connected two at a time at their endpoints.
    [Show full text]
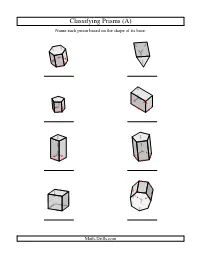
  • Geometry Worksheet -- Classifying Prisms
    Classifying Prisms (A) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (A) Answers Name each prism based on the shape of its base. hexagonal prism triangular prism pentagonal prism rectangular prism square prism pentagonal prism square prism, cube heptagonal prism Math-Drills.com Classifying Prisms (B) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (B) Answers Name each prism based on the shape of its base. hexagonal prism octagonal prism heptagonal prism rectangular prism square prism, cube hexagonal prism triangular prism square prism Math-Drills.com Classifying Prisms (C) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (C) Answers Name each prism based on the shape of its base. octagonal prism square prism rectangular prism square prism triangular prism square prism, cube heptagonal prism hexagonal prism Math-Drills.com Classifying Prisms (D) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (D) Answers Name each prism based on the shape of its base. hexagonal prism square prism octagonal prism pentagonal prism rectangular prism square prism, cube hexagonal prism triangular prism Math-Drills.com Classifying Prisms (E) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (E) Answers Name each prism based on the shape of its base. pentagonal prism square prism, cube square prism heptagonal prism rectangular prism pentagonal prism triangular prism octagonal prism Math-Drills.com Classifying Prisms (F) Name each prism based on the shape of its base.
    [Show full text]
  • Experimental and Theoretical Statics of Liquids Subject to Molecular
    EXPERIMENTAL AND THEORETICAL STATICS OF LIQUIDS SUBJECT TO MOLECULAR FORCES ONLY, BY J. PLATEAU Professor of the University of Ghent, Member of the Academy of Belgium, Correspondent of the Institute of France, of the Royal Society of London, of the Berlin Academy, etc. VOLUME ONE. PARIS, LONDON, GAUTHIER-VILLARS, TRÜBNER and Co, quai des Augustine, 55. Ludgate Hill, 57 and 59. GAND ET LEIPZIG: F. CLEMM. 1873. TO MONSIEUR A. QUETELET DIRECTOR OF THE OBSERVATORY OF BRUSSELS , ETC. You, who were one of the active promoters of the intellectual regeneration of Bel- gium, and whose work contributed so much to the illustriousness of this country; you, who guided my first steps in the career of science, and who taught me, by your exam- ple, to excite among young people the love of research, who did not cease being for me a devoted friend, allow me to dedicate this work to you, in testimony of recognition and constant affection. J. PLATEAU. This work is formed primarily of the contents of eleven Series of Memoires that I published, from 1843 to 1868, in the Memoires of the Academy of Belgium, under the title: Research experimental and theoretical on the equilibrium shapes of a liquid mass without gravity1. But the revision of the whole of these Series enabled me to follow, in the current work, an order a little more methodical, to rectify some passages, and to fill gaps, especially in the histories; until the end of 1869, I could extend I did of them two those new, one concerning the surface viscosity of liquids, the other with the constitution of liquid streams; I introduced several additions which appear worthy to me of interest, such as the theory of exploding laminar bubbles; on the other hand, I removed, as concerning purely dynamic phenomena, the majority of the results of my first Series; finally I have indicated, in a last paragraph, the titles of the articles which appeared after 1869 on subjects in connection with those that I treat.
    [Show full text]