DOCSLIB.ORG

Charge and Exciton Transport in DNA

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Charge and Exciton Transport in DNA Abstract Charge and Exciton Transport in DNA by Rajesh Shresth Doctor of Philosophy in Chemistry Tulane University Alexander L. Burin, Chair The rate of charge transfer and the degree of excited state delocalization in homogeneous DNA bases are investigated theoretically and computationally. In the first part molecular dynamics simulation is used to calculate the reorganization energy associated with charge transfer. The reorganization energy includes high frequency quantum vibrations only fractions of which contribute to charge transfer. Small polaron theory is used to rescale the quantum vibration contribution to reorganization energy and the subsequent charge transfer rate calculated using this quantum corrected reorganization energy is in some case in better agreement with the experiment. Also the RESP charges of AT and GC base pairs used in molecular dynamics is compared with the Mullikan charges obtained from DFT calculation. The RESP charges show that the oxidized AT base pair is more delocalized than oxidized GC base pair. This trend is opposite of what is observed for Mullikan charge obtained from DFT calculation. In the second part degree of excited state delocalization in homogeneous GC strand is calculated. Exciton coupling value between two adjacent GC base pairs that dictates the degree of delocalization is evaluated by fitting Van Vleck sum rule model to the experimental absorption and circular dichroism data. Furthermore the reorganization energy associated with exciton formation is calculated computationally and is used along with exciton coupling value to numerically obtain the degree of excited state delocalization in homogenous GC strand. Dedicated to my parents Acknowledgments I would like to express my deepest gratitude to my advisor, Dr. Alexander Burin for his excellent guidance and continuous encouragement during my time at Tulane University. I have been very fortunate to have a graduate advisor who gave me freedom to venture on my own. My development as a researcher and completion of this dissertation would not have been possible without his support. I would also like to thank the Department of Chemistry at Tulane University and especially the members of my dissertation committee. Furthermore, I would like to ac- knowledge my co-workers, John Leveritt and Arkady Kurnosov, Sarah Tesar and Gale Blaustein for insightful discussion and collaborating on research projects. I appreciate the financial support I received during my graduate studies at Tulane University. I thank Tulane University School of Science and Engineering and Department of Chemistry, the IBM Computational Science Fellowship Program and the National Science Foundation. I am fortunate to have a tight-knit extended family. They have helped me overcome setbacks and stay focused on my graduate study. I am forever indebted to them for their unending love and support. I am also grateful to all my friends for providing support and friendship that I needed. ii Contents I Molecular Dynamics Study of Charge Transfer in DNA 2 1.1 Background: . 3 1.2 Theoretical Model: . 4 1.3 Computational Model: . 9 1.3.1 Force Field: . 9 1.3.2 Numerical Algorithm: . 10 1.3.3 Solvent: . 11 1.3.4 Charge Derivation: . 12 1.3.5 Periodic Boundary Condition: . 13 1.3.6 Non-Bonded Interaction: . 13 1.3.7 Barostat: . 14 1.3.8 Thermostat: . 15 1.4 Calculation and Result: . 16 1.4.1 Monitoring MD simulation: . 17 1.4.2 Reorganization energy calculation: . 28 1.4.3 Decomposition of reorganization energy: . 29 1.4.4 Time Correlation Function: . 34 1.4.5 Rate of hole transfer: . 37 1.5 Conclusion: . 39 II Exciton Delocalization in DNA 41 2.1 Background: . 42 2.2 Theory: . 43 2.3 Experimental Data and Calculations: . 47 2.3.1 Exciton Coupling Calculations: . 51 iii 2.3.2 Inhomogeneous Broadening Calculation: . 52 2.3.3 Exciton Delocalization Length: . 57 2.4 Conclusion: . 61 A Charges for driving force calculations: 62 A.1 Neutral charges in GC and AT base pair used in MD: . 63 A.2 GC RESP charge used for driving force calculation: . 64 A.3 GC DFT charge used for driving force calculation: . 65 A.4 AT RESP charge used for driving force calculation: . 66 A.5 AT DFT charge used for driving force calculation: . 67 B Code for calculating hole transfer in identical adjacent DNA bases. 68 B.1 Fortran code to calculate driving force . 69 B.2 Matlab/Octave code for calculatin reorganization energy: . 74 B.3 Matlab/Octave code to calculate correlation function . 76 B.4 Matlab/Octave code to rearrange the charges. 77 C Detailed equation used for calculating driving force 79 D Program in Matlab to create a structure of GC dimer 82 E ZINDO spectrum of monomer and dimer GC Watson-Crick base pair 84 E.1 Excitation energies and oscillator strengths of GC base pair . 85 E.2 Excitation energies and oscillator strengths of stacked GC Dimer . 87 F Program in Scilab to calculate delocalization length 90 Bibliography 96 iv List of Tables 1.1 Reorganization energy . 29 1.2 Decomposition of reorganization energy different two frequency components 34 1.3 Decay Constants . 36 1.4 Characteristic relaxation time . 37 1.5 Classical rate of hole transfer . 37 1.6 Quantum corrected hole transfer rate . 38 1.7 Correlation between charge localization and reorganization energy . 39 2.8 Reorganization Energy associated with GC S0 − S1excitation. 55 2.9 Delocalization length and its dependence on site-energy. 60 A.1 Neutral charges in GC and AT base pair used in MD: . 63 A.2 GC RESP charge used for driving force calculation. 64 A.3 GC RESP charge used for driving force calculation. 65 A.4 GC RESP charge used for driving force calculation. 66 A.5 GC RESP charge used for driving force calculation. 67 v List of Figures 1.1 Convergence in time of the energy of the system . 18 1.2 Convergence in time of the temperature of the system . 19 1.3 Convergence in time of the pressure of the system . 21 1.4 Convergence in time of the volume of the system . 22 1.5 Convergence in time of the density of the system . 23 1.6 Convergence in time of the RSMD of the system . 25 1.7 Fluctuation in driving force in DNA . 26 1.8 Fluctuation in driving force in DNA . 27 1.9 The normalized spectral density functions J(ω). 30 1.10 The normalized spectral density functions J(ω). 31 1.11 The normalized spectral density functions J(ω). 32 1.12 The normalized spectral density functions J(ω). 33 1.13 Time Correlation Function . 35 1.14 Time Correlation Function . 35 2.15 Skeletal structure of C12−linked DNA hairpins. 48 2.16 Absorption spectra of C12−linked DNA hairpins . 49 2.17 Circular dichroism spectra of C12−linked DNA hairpins. 50 2.18 Schematic diagram of exciton coupling . 53 2.19 Electronic states of GC associated with absorption and fluorescence cycle. 54 2.20 Gaussian fitting of absorption of spectrum of a GC hairpin . 56 C.1 DNA base numbering convention used in our molecular dynamics simulation. 80 vi 1 Introduction In 1953, Waston and Crick showed that DNA has double helix spiral staircase like structure with base pairs acting as rungs. Soon after that discovery Eley and Spivey suggested that pi-stacking interaction between the adjacent bases could allow DNA to conduct charge [1]. However, subsequent experimental progress in the understanding of the electronic property of DNA languished due to difficulty in obtaining DNA in desired quantity and sequence from natural sources; and efficient synthesis of DNA was not pos- sible for two more decades until the breakthrough in phosphoramidite chemistry in early 1983 [2]. Interest in this field was rekindled after the pioneering work of Barton et al. in 1993, where she showed photoinduced long range DNA mediated charge transfer between non-covalently bound metallointercalators [3]. Since then there have been numerous the- oretical and experimental studies in charge and energy transfer property of DNA and the interest in the field is growing rapidly due the possibility of using it in nano-electronics [4], electrochemical biosensors [5], harnessing solar energy [6], repairing oxidative damage in DNA [7], economical DNA sequencing [8]etc. This dissertation “Charge and Energy transfer in DNA,” is a theoretical and computa- tional investigation of charge transfer rate and energy transfer parameter in homogenous DNA sequence. In part I, the quantum effect in the absolute rate of charge transfer between homogeneous adjacent DNA bases is examined. Understanding of hole transfer rate has application in desigining nanowires. In part II, the exciton coupling paramater is calculated by fitting our theroy to an exprimental data. Excion coupling paramater eluci- dates the excited state delocalization behavior of DNA and its understanding is important to use DNA for harnessing solar energy and repairing photodamage in DNA. 2 Part I Molecular Dynamics Study of Charge Transfer in DNA 3 1.1 Background: Theoretical studies of charge transfer in DNA are generally conducted using semi- classical Marcus’ theory [9], where coupling between donor and acceptor in the pre- exponential term is treated quantum mechanically and the reorganization energy in ex- ponential term is treated classically. Marcus equation has a form that looks very much like an Arrhenius equation for the temperature dependence of rate of chemical reaction. k = A.e−Ea/kbT (1.1) where Ea is the activation energy that needs to be overcome by thermal energy kbT for the reaction to occur. For the charge transfer reactions Marcus showed that the activation energy itself depends on solvent reorganization energy and Gibbs free energy difference between the reactant and the product 2 − (λ+4G) k = A.e 4λkbT (1.2) Here ∆G is the Gibbs free energy of reaction, the prefactor A depends upon the strength of the electronic interaction between donor and acceptor and the type of charge transfer, and λ is the reorganization energy that accounts for the structural reorganization of donor- acceptor molecules and the surrounding solvent molecules.
Load more

Recommended publications
  • Prospectus 2020
    RAMAKRISHNA MISSION VIVEKANANDA CENTENARY COLLEGE Rahara, Kolkata 700 118 An Autonomous College under WBSU College with Potential for Excellence (CPE) Accredited by NAAC with Grade-A With Post-Graduate Section Secured All India Rank 8 in NIRF 2019 Prospectus 2020 History: • The Ramakrishna Mission Boys‟ Home at Rahara, a branch centre of the Ramakrishna Mission, was founded in 1944 as an orphanage with a nucleus of 37 boys rendered orphan by the Great Bengal Famine of 1942-1943. Since then the Home grew in dimensions and activities adhering to the principle of service to mankind in the spirit of worship. Today, the Home is an educational complex with several schools and colleges wherein nearly four thousand students are receiving education and training in different subjects and trades according to the aptitude of each individual. • This College which forms an integral part and unit of this educational complex is owned and managed by the Ramakrishna Mission. The foundation stone of the College was laid by Swami Vireswaranandaji Maharaj, the then General Secretary of the Ramakrishna Mission, on 3rd December, 1961 and the College started functional in July, 1963. • The College was established with a view to commemorating the First Birth Centenary of Swami Vivekananda, the Illustration Patriot-Saint of India and with a view to imparting a general education on a religious background in the light of the teachings of Ramakrishna - Vivekananda so that the young pupils may get ample opportunities to build up their character to make themselves useful to their families and to fulfil at the same time their basic obligation to the country.
    [Show full text]
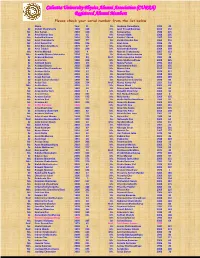
  • Calcutta University Physics Alumni Association (CUPAA) Registered Alumni Members Please Check Your Serial Number from the List Below Name Year Sl
    Calcutta University Physics Alumni Association (CUPAA) Registered Alumni Members Please check your serial number from the list below Name Year Sl. Dr. Joydeep Chowdhury 1993 45 Dr. Abhijit Chakraborty 1990 128 Mr. Jyoti Prasad Banerjee 2010 152 Mr. Abir Sarkar 2010 150 Dr. Kalpana Das 1988 215 Dr. Amal Kumar Das 1991 15 Mr. Kartick Malik 2008 205 Ms. Ambalika Biswas 2010 176 Prof. Kartik C Ghosh 1987 109 Mr. Amit Chakraborty 2007 77 Dr. Kartik Chandra Das 1960 210 Mr. Amit Kumar Pal 2006 136 Dr. Keya Bose 1986 25 Mr. Amit Roy Chowdhury 1979 47 Ms. Keya Chanda 2006 148 Dr. Amit Tribedi 2002 228 Mr. Krishnendu Nandy 2009 209 Ms. Amrita Mandal 2005 4 Mr. Mainak Chakraborty 2007 153 Mrs. Anamika Manna Majumder 2004 95 Dr. Maitree Bhattacharyya 1983 16 Dr. Anasuya Barman 2000 84 Prof. Maitreyee Saha Sarkar 1982 48 Dr. Anima Sen 1968 212 Ms. Mala Mukhopadhyay 2008 225 Dr. Animesh Kuley 2003 29 Dr. Malay Purkait 1992 144 Dr. Anindya Biswas 2002 188 Mr. Manabendra Kuiri 2010 155 Ms. Anindya Roy Chowdhury 2003 63 Mr. Manas Saha 2010 160 Dr. Anirban Guha 2000 57 Dr. Manasi Das 1974 117 Dr. Anirban Saha 2003 51 Dr. Manik Pradhan 1998 129 Dr. Anjan Barman 1990 66 Ms. Manjari Gupta 2006 189 Dr. Anjan Kumar Chandra 1999 98 Dr. Manjusha Sinha (Bera) 1970 89 Dr. Ankan Das 2000 224 Prof. Manoj Kumar Pal 1951 218 Mrs. Ankita Bose 2003 52 Mr. Manoj Marik 2005 81 Dr. Ansuman Lahiri 1982 39 Dr. Manorama Chatterjee 1982 44 Mr. Anup Kumar Bera 2004 3 Mr.
    [Show full text]
  • Year 2016-17
    110 108.97 96 90 70 60.91 DST 50 WB Govt. 30.23 30 20.93 24.39 Project 10 2.96 4.01 4.13 -10 Grant - 2014-15 Grant - 2015-16 Grant - 2016-17 Budget in 2016-17 : DST – 108.97 crores; WB Government – 4.13 crores Web of Science Citation Report (On 19th July, 2017) Result found 1983-2017 No. of Publications : 9939 H Index : 115 Sum of the times cited : 158271 Average citations per item : 15.92 Average citations per year : 4522.03 Performance during the year (2016-17) Publication : 444 Average Impact Factor : 4.4 Ph.D. Degree Awarded : 58 Patent Awarded : 04 Patent Filed : 14 I A C S ANNUAL REPORT 2016 - 2017 INDIAN ASSOCIATION FOR THE CULTIVATION OF SCIENCE Contents From the Director’s Desk ....................................................................... 004 The Past Glory ....................................................................................... 006 The Laurels - Faculty Members ............................................................. 012 The Laurels - Research Fellows ............................................................. 013 Key Committees .................................................................................... 014 Executive Summary ............................................................................... 017 Biological Chemistry .............................................................................. 022 Centre For Advance Materials ............................................................... 031 Director’s Research Unit .......................................................................
    [Show full text]
  • Annual Report 2017-2018
    ANNUAL REPORT IISc 2017-18 INDIAN INSTITUTE OF SCIENCE VISITOR The President of India PRESIDENT OF THE COURT N Chandrasekaran CHAIRMAN OF THE COUNCIL P Rama Rao DIRECTOR Anurag Kumar DEANS SCIENCE: Biman Bagchi ENGINEERING: K Kesava Rao UG PROGRAMME: Anjali A Karande REGISTRAR V Rajarajan Pg 3 IISc RANKED INDIA’S TOP UNIVERSITY In 2016, IISc was ranked Number 1 among universities by the National Institutional Ranking Framework (NIRF) under the auspices of the Ministry of Human Resource Development. It was the first time the NIRF came out with rankings for Indian universities and institutions of higher education. In both 2017 and 2018, the Institute was again ranked first among universities, as well as first in the overall category. CONTENTS Foreword IISc at a Glance 8 1. The Institute 18 Court 5 Council 20 Finance Committee 21 Senate 21 Faculties 21 2. Staff (administration) 22 3. Divisions 25 3.1 Biological Sciences 26 3.2 Chemical Sciences 58 3.3 Electrical, Electronics, and Computer Sciences 86 3.4 Interdisciplinary Research 110 3.5 Mechanical Sciences 140 3.6 Physical and Mathematical Science 180 3.7 Centres under the Director 206 4. Undergraduate Programme 252 5. Awards/Distinctions 254 6. Students 266 6.1 Admissions & On Roll 267 6.2 SC/ST Students 267 6.3 Scholarships/Fellowships 267 6.4 Assistance Programme 267 6.5 Students Council 267 6.6 Hostels 267 6.7 Institute Medals 268 6.8 Awards & Distinctions 269 6.9 Placement 279 6.10 External Registration Program 279 6.11 Research Conferments 280 7. Events 300 7.1 Institute Lectures 310 7.2 Conferences/Seminars/Symposia/Workshops 302 8.
    [Show full text]
  • Statistical Mechanics in Theoretical Chemistry in India
    Proc Indian Natn Sci Acad 86 No. 2 June 2020 pp. 903-909 Printed in India. DOI: 10.16943/ptinsa/2019/49727 Review Article Statistical Mechanics in Theoretical Chemistry in India: Past, Present and A Bit of Future AMALENDU CHANDRA1,* and BIMAN BAGCHI2,* 1Department of Chemistry, Indian Institute of Technology Kanpur, Kanpur 208 016, India 2Solid State and Structural Chemistry Unit, Indian Institute of Science, Bangalore 560 012, India (Received on 03 March 2019; Revised on 25 May 2019; Accepted on 05 June 2019) While the subject of statistical mechanics is intensely active in physics departments across India, with considerable activity even in mathematics departments, the same cannot be said for average chemistry departments in India where statistical mechanics is relatively less taught and even less pursued. This is to be contrasted with USA and many other developed countries (Germany, Israel) where statistical mechanics and spectroscopy are major disciplines in the physical chemistry departments. The situation, however, has changed rapidly in the past few decades. In this article we discuss the developments in this important area in the recent past, with emphasis both on analytical approach and those based on computer simulations. We also attempt to look into future problems where our efforts could be directed fruitfully. Keywords: Theoretical Chemistry; Physical Chemistry; Statistical Mechanics; Molecular Simulations; Chemical Dynamics It is often said that chemistry means chemical of Zeolites and/or other such species by hydrothermal reactions, and most of the chemical reactions occur reactions, one can control the formation of the desired in the solution phase. Many of the biochemical product by tuning the temperature and the processes that sustain all forms of life occur in liquids concentration.
    [Show full text]
  • Tribute to Biman Bagchi Laser Spectroscopic Groups of One of Us (G.R.F.), Paul Barbara, and Others
    Special Issue Preface pubs.acs.org/JPCB Tribute to Biman Bagchi laser spectroscopic groups of one of us (G.R.F.), Paul Barbara, and others. The solvation dynamics was reported to have times scales faster than dielectric relaxation, which posed a challenge to theorists for proper explanations. Just before joining IISc, Bagchi, in collaboration with G.R.F. and David Oxtoby, had developed a theory of dipolar solvation using a continuum model of the solvent and a frequency dependent dielectric function. The theory predicted a solvation time that was faster than the dielectric relaxation time of the solvent, thus providing an explanation of the experimentally observed fast relaxation of the time dependent solvation energy. The continuum theory was subsequently generalized by Bagchi and co-workers in many different directions such as incorporation of multi-Debye relaxation, non-Debye relaxation, inhomogeneity of the medium around a solute, etc. Still, being based on continuum models, all these extensions lacked the molecularity of the solvent. Besides, these theories considered only the rotational motion of solvent molecules because the dynamics came through the frequency Photo by S. R. Prasad dependence of the long wavelength dielectric function. Micro- rofessor Biman Bagchi has made pivotal contributions to the scopic theories based on molecular solvent models also started P area of dynamics of chemical and biological systems in an coming from other groups; however, these microscopic theories academic career spanning more than three decades. He has been also included only the rotational motion of solvent molecules. a great teacher and mentor for a large number of young These rotation-only microscopic theories predicted an average theoretical physical chemists of India and a creative and insightful solvation time that was longer than the long-wavelength fi collaborator with leading scientists worldwide.
    [Show full text]
  • Volume Content 1..11
    Journal of Chemical Sciences [Formerly: Proceedings of the Indian Academy of Sciences (Chemical Sciences)] Volume 124, 2012 CONTENTS Special issue on Structure, Reactivity and Dynamics Foreword 11–12 Dynamics of atom tunnelling in a symmetric double well coupled to an asymmetric double well: The case of malonaldehyde S Ghosh and S P Bhattacharyya 13–19 Shape change as entropic phase transition: A study using Jarzynski relation Moupriya Das, Debasish Mondal and Deb Shankar Ray 21–28 Fitness landscapes in natural rocks system evolution: A conceptual DFT treatment Soma Duley, Jean-Louis Vigneresse and Pratim Kumar Chattaraj 29–34 Hydrogen bonded networks in formamide [HCONH2]n (n ¼ 1 − 10) clusters: A computational exploration of preferred aggregation patterns A Subha Mahadevi, Y Indra Neela and G Narahari Sastry 35–42 Use of an intense microwave laser to dissociate a diatomic molecule: Theoretical prediction of dissociation dynamics Amita Wadehra and B M Deb 43–50 + A quantum-classical simulation of a multi-surface multi-mode nuclear dynamics on C6H6 incorporating degeneracy among electronic states Subhankar Sardar and Satrajit Adhikari 51–58 Understanding proton affinity of tyrosine sidechain in hydrophobic confinement T G Abi, T Karmakar and S Taraphder 59–63 Full dimensional quantum scattering study of the H2 þ CN reaction S Bhattacharya, A Kirwai, Aditya N Panda and H-D Meyer 65–73 Dynamics of atomic clusters in intense optical fields of ultrashort duration Deepak Mathur and Firoz A Rajgara 75–81 Bhageerath—Targeting the near impossible:
    [Show full text]
  • Abstract Book
    26th CRSI-National Symposium in Chemistry CRSI-NSC-26 February 07-09, 2020 Abstract Book Jointly Organized by Department of Chemistry VIT Vellore, CRSI, & RSC, UK Contents Welcome Organizing Committee Message from Founder President, CRSI Message from Founder Chancellor, VIT Message from Pro Vice Chancellor, VIT Message from President, CRSI Message from Dean, School of Advance Science Acknowledgements Program Abstracts President’s Lecture Animesh Chakravorty Endowment Lecture CRSI Medal Lecture C. N. R. Rao National Prize for Chemical Research CRSI Honorary Fellowship Lecture C. N. R. Rao Award Lecture Silver Medal Lecture Mizushima - Raman Lecture Third Charusita Chakravarty Memorial Lecture Lifetime Achievement Award Lecture Bronze Medal Lectures Invited Lectures Abstracts Posters Welcome Message from Organizers On behalf of organizing committee of the 26th National Symposium in Chemistry (NSC) and 14th Royal Society of Chemistry Joint Symposium under the auspices of the Chemical Research Society of India (CRSI), we are delighted to welcome you to the symposium and to the Vellore Institute of Technology Vellore. The 26th CRSI-NSC meeting is attended by a large number of scientists, academicians and students from universities and academic/research institutions spread across the length and breadth of India. The meeting is attended by nearly 200 registered participants. The symposium has 34 lectures that include CRSI medal lectures, special lectures. More than 130 posters will be presented by faculty and students. The Royal Society of Chemistry, UK has been partnering with CRSI in organizing a one day symposium, along with the CRSI National Symposium over the years. This year also, there will be a CRSI-RSC symposium on February 6, 2020, preceding the CRSI National Symposium at Vellore.
    [Show full text]
  • Archive-Mashelkar Endowment Lectures (May 2011-Jan 2015) Sr No
    Archive-Mashelkar Endowment Lectures (May 2011-Jan 2015) Sr No. Date Speaker Name Title and Abstract 1 30-May-11 Prof. Biman Bagchi Title: Single Molecular View of Biological Processes : Protein-DNAInteraction, Enzyme Kinetics and Kinetic Proof Reading Abstract : Complexity of biological processes often does not allow a molecular level understanding of important dynamical events. However, recent single molecule spectroscopic studies have revealed new and fascinating aspects of several age-old problems that motivated new theoretical developments. In this talk I shall discuss our recent work on several such important biological processes, namely (a) the mechanism of diffusion of a non-specifically bound protein along DNA in its search for the specific binding site, and (b) the role of enzyme fluctuations in enzyme catalysis and, (c) explicit role of water in enzyme kinetics, and (d) theory of kinetic proof reading or, theory of lack of errors in biological synthesis within cells. 2 16-Jun-11 Prof Yamuna Krishnan Title: Molecular DNA devices in Living Systems Abstract : DNA has attractive physicochemical characteristics such as robust thermal and hydrolytic stability. It also has desirable structural characteristics stemming from predictable and specific recognition properties that give rise to a highly regular helical structure which behaves as a rigid rod on length scales upto ~50 nm. Since these rigid rods may be welded together by complementary base-pairing, DNA is now taking on a new aspect where it is finding use as a construction element to build exquisitely complex architectures on the nanoscale. This field is called structural DNA nanotechnology. We have been interested in architecturally simple, yet functional DNA-based molecular devices.
    [Show full text]
  • Science & Engineering Research Board
    Science & Engineering Research Board List of Projects Sanctioned in the Year 2015-16 S.No. Scheme Title PI Name Institute & Address Total Cost 1 EMR Development of Sugar amino Dr.Ravi Shankar Central Drug Research 2660000 acid derived peptides self - Ampapathi Institute Lucknow 226031 assembling selectively on Uttar Pradesh bacterial membrances ,forming ion pores and killing bacteria including MTB 2 EMR Development of Sugar amino Prof.Tushar Kanti Indian Institute of Science 6384000 acid derived peptides self - Chakraborty Bangalore 560012 assembling selectively on Karnataka bacterial membrances ,forming ion pores and killing bacteria including MTB 3 EMR Band gap tuning of transtion Dr.SanjibKarmakar Gauhati University 1588800 metal oxides (ZnO,NiO, Guwahati 781014 Assam CuO,Fe2O3 )nanoparticles by Controlling microstrain and doping concentrations 4 EMR Investigation of physical aging in Dr.Asmita Sengupta Visva -Bharati Central 1553520 High Tg polymers by the University Bolpur combination of PSPLS & DSC Santiniketan 731235 West methods Bengal 5 EMR Investigation of ultiferroic Dr.I.B.Shameem Banu B.S.Abdur Rahman 2355300 properties of rere earth and University Chennai 600048 transtion metal doped Bismuth Tamilnadu ferrite for functional applications 6 EMR An Artifical muscle based on Prof.M.R.Anantharam Cochin University of 4613200 Ferrogel fibers an Science And Technology Cochin 682022 Kerala 7 EMR Investigations of RM Magnetron Dr.R.Balasundaraprab PSG College of Technology 3476800 Sputtered Cu2ZnSnS4 (CZTS) hu Coimbatore 641004 Absorder layer for sustainable Tamilnadu solar cell applications 8 EMR Multiscale modelling of complex Dr.Santosh Ansumali Jawaharlal Nehru Centre 4936800 fluids for Advanced Scientific Research Bangalore 560064 Karnataka 9 EMR Non -Linear Dynamics Prof.
    [Show full text]
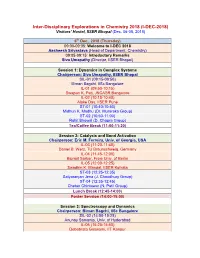
  • I-DEC-2018) Visitors’ Hostel, IISER Bhopal (Dec
    Inter-Disciplinary Explorations in Chemistry 2018 (I-DEC-2018) Visitors’ Hostel, IISER Bhopal (Dec. 06-08, 2018) 6th Dec., 2018 (Thursday) 09:00-09:05: Welcome to I-DEC 2018 Aasheesh Srivastava (Head of Department, Chemistry) 09:05-09:15: Introductory Remarks Siva Umapathy (Director, IISER Bhopal) Session 1: Dynamics in Complex Systems Chairperson: Siva Umapathy, IISER Bhopal SIL-01 (09:15-09:50) Biman Bagchi, IISc Bangalore IL-01 (09:50-10:15) Swapan K. Pati, JNCASR Bangalore IL-02 (10:15-10:40) Aloke Das, IISER Pune ST-01 (10:40-10:50) Midhun K. Madhu (Dr. Muraraka Group) ST-02 (10:50-11:00) Rohit Bhowal (D. Chopra Group) Tea/Coffee Break (11:00-11:20) Session 2: Catalysis and Bond Activation Chairperson: Eric M. Ferreira, Univ. of Georgia, USA IL-03 (11:20-11:45) Daniel B. Werz, TU Braunschweig, Germany IL-04 (11:45-12:00) Biprajit Sarkar, Freie Univ. of Berlin IL-05 (12:00-12:25) Swadhin K. Mandal, IISER Kolkata ST-03 (12:25-12:35) Satyaranjan Jena (J. Choudhury Group) ST-04 (12:35-12:45) Chetan Chintawar (N. Patil Group) Lunch Break (12:45-14:00) Poster Session (14:00-15:00) Session 3: Spectroscopy and Dynamics Chairperson: Biman Bagchi, IISc Bangalore SIL-02 (14:50-15:25) Anunay Samanta, Univ. of Hyderabad IL-06 (15:25-15:50) Debabrata Goswami, IIT Kanpur IL-07 (15:50-16:15) Arindam Chowdhury, IIT Bombay ST-05 (16:15-16:25) Chiranjit Ghosh (M. Kapur Group) ST-06 (16:25-16:35) Sibaram Panda (P.
    [Show full text]
  • Form 5 Report for JSPS Asian Academic Seminar FY2014
    Form 5 Report for JSPS Asian Academic Seminar FY2014 <Summary> Date March 31, 2015 1. Title of Seminar JSPS-DST Asia Academic Seminar: Structure, Dynamics, and Functionality of Molecules and Materials 2. Purpose of Seminar The Asia Academic Seminar is organized under the auspices of the Japan Society of Promotion of Science (JSPS) in Japan and the Department of Science and Technology (DST) in India. It has been held since 1994 in different fields of science in different Asian countries. The seminar is one of the most important programs for enhancing the research activities of young scientists in Asian countries. It is designed to spur scientific achievement in the region by introducing the latest scientific advances to young Asian researchers. The title of the present seminar was “Spectroscopy, Theoretical Chemistry and Chemistry of Materials”. Recent development of ultrafast spectroscopy including time-resolved X-ray diffraction techniques makes it possible to probe structural changes induced by external fields as well as detailed fluctuation and dynamics. In addition, various measurement techniques for dynamics with combination of electronic, magnetic, and other properties have been developed. Understanding of the dynamics of molecules and materials is essential for elucidation, control, and application of the functionalities. Furthermore, it is also required to develop new material science, which leads to structural and functional designs of novel materials. In the seminar, which is about structure, dynamics, and functionality of molecules, recent cutting edge scientific results were presented by world-renowned invited lecturers. In addition, people exchanges between lecturers and attendees in the seminar contribute to the educational activities.
    [Show full text]