DOCSLIB.ORG

Proposed One-Minute Rain Rate Conversion Method for Microwave Applications in Korea

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Proposed One-Minute Rain Rate Conversion Method for Microwave Applications in Korea J. lnf. Commun. Converg. Eng. 14(3): 153-162, Sep. 2016 Regular paper Proposed One-Minute Rain Rate Conversion Method for Microwave Applications in Korea Sujan Shrestha and Dong-You Choi*, Member, KIICE Department of Information and Communications Engineering, Chosun University, Gwangju 61452, Korea Abstract Microwave and millimeter waves are considered suitable frequency ranges for diverse applications. The prediction of rain attenuation required the 1-min rainfall rate distribution, particularly for data obtained locally from experimental measurement campaigns over a given location. Rainfall rate data acquired from Korea Meteorological Administration (KMA) for nine major sites are analyzed to investigate the statistical stability of the cumulative distribution of rainfall rate, as obtained from a 10-year measurement. In this study, we use the following rain rate conversion techniques: Segal, Burgueno et al., Chebil and Rahman, exponential, and proposed global coefficient methods. The performance of the proposed technique is tested against that of the existing rain rate conversion techniques. The nine sites considered for the average 1-min rain rate derivation are Gwangju, Daegu, Daejeon, Busan, Seogwipo, Seoul, Ulsan, Incheon, and Chuncheon. In this paper, we propose a conversion technique for a suitable estimation of the 1-min rainfall rate distribution. Index Terms: 1-Minute rain rate, Microwave communication, Rain rate model I. INTRODUCTION application to the prediction of experimental local data remains challenging [2]. Efforts to localize rain attenuation The advancement of technologies in the fields of satellite models however depend on the knowledge of the rainfall communications, multimedia applications, the Internet, and rate and the experimental data for the chosen location. The mobile communications has increased the demand for a high data further enhance the development of the local rain data transmission rate. Consequently, in the field of data attenuation model. In this paper, the experimental result of transmission technology, the emphasis has shifted to high- rainfall rate statistics of certain selected locations of Korea frequency microwave bands. However, the problem of rain is described. According to climatologists, recently, major is significant for operation frequencies of more than 10 GHz. cities in Korea have experienced unusually heavy rainfall, A reduction in the transmitted signal amplitude because of which might be attributed to urban heat island phenomena an atmospheric mechanism such as the absorption and [3]. A comprehensive effort for the characterization of scattering of radio waves results in rain attenuation [1]. the 1-min rainfall rate has been made by International Further, a communication system designer faces a problem Telecommunication Union Radiocommunication Study in the prediction of the effects of rain on radar and the Group 3 (ITU-R, formerly the CCIR). Moreover, to convert remote sensing of a location on or above the Earth’s surface. a relatively high integration time’s rainfall data to the Although numerous rain attenuation models exist, their equivalent 1-min distribution, various procedures have been ___________________________________________________________________________________________ Received 05 July 2016, Revised 06 July 2016, Accepted 02 August 2016 *Corresponding Author Dong-You Choi (E-mail: [email protected], Tel: +82-62-203-7060) Department of Information and Communications Engineering, Chosun University, 309, Pilmun-daero, Dong-gu, Gwangju 61452, Korea. Open Access http://dx.doi.org/10.6109/jicce.2016.14.3.153 print ISSN: 2234-8255 online ISSN: 2234-8883 This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by- nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited. Copyright ⓒ The Korea Institute of Information and Communication Engineering 153 J. lnf. Commun. Converg. Eng. 14(3): 153-162, Sep. 2016 enforced considering the relevant physical, analytical, and RSC) method is used for the conversion of the rainfall rate empirical models [4]. Because of the experimental statistics from a long integration time to a 1-min integration dependence and for simplicity, in this study, empirical time. This method is based on the simulated movement of models are selected as an appropriate method for rain cells over a virtual rain gauge, during the given determining the distribution of the rainfall rate at the 1-min integration time T, whose translation velocity depends on integration time. Further, in this paper, we emphasize on the both the type of precipitation and the observation period. difference between the measured rainfall rate statistics and The rainfall conversion is obtained using a virtual rain the ITU-R P.837-6 [5] model along with the applicable gauge according to the local mean yearly wind velocity, empirical nature methods. which is extracted from the ERA-40 database. The The rest of the paper is organized as follows: Section II prediction approach is based on the annual rainfall amount presents a brief overview of the predicted point rainfall rate. of the convective type and the stratiform type along with the The experimental setup is described in Section III. Section probability of 6-hr rainy periods. Depending on the type of IV highlights the performed regression analyses for the precipitation, rain structures appear to move mostly because applicable empirical methods. Similarly, Section V details of the wind speed (convective rain) or because of the time the performance evaluation of the proposed technique. evolution (stratiform rain) [14]. The theoretical concept of Finally, Section VI draws some useful conclusions. this model is explained using a physical model-based methodology in [15] and in an update of Recommendation ITU-R P.837-5, Annex 3 [5]. EXCELL RSC is globally II. REVIEW OF SELECT 1-MIN RAIN RATE applicable and has strong physical soundness for CONVERSION MODELS measurements with an arbitrary integration time, T. The effectiveness of the EXCELL RSC model was tested using Several studies have been conducted to measure the effect various error analyses against other global models in [16], of this natural phenomenon on the radio propagation path where the EXCELL RSC model was found to be suitable for above 10 GHz, using the various rain attenuation statistical the estimation of the 1-min rainfall rate. models either globally or locally. Further, a considerable Several researchers around the globe have proposed amount of research work has been carried out in this area regional rainfall rate models. These rainfall rate models over the years locally [3, 6-10]. Interestingly, the have been developed from empirical equations using the experimental duration of the rainfall rate data is relatively results of field measurements collected over a long period of low, and more research needs to be carried out to ensure a time [12]. Similarly, the mathematical theory based on the reliable signal transmission. Furthermore, the rainfall rate principles for de-integrating a T-min experimental research carried out in the neighboring country Japan [11] probability distribution (pd) into the corresponding 1-min pd relies on the thunderstorm ratio and the regional climatic is presented in [17]. However, there is a need for more parameters of only one location of Korea as Daejeon. efficient propagation planning, based on the use of the Because of the variations in the performed experiment, this number and the duration of rain events along with the model has not been analyzed, but the exponential nature of fraction of the rain time. The experimental system used by rain rate variation has been studied. Rainfall rate models are Korea Meteorological Administration (KMA) provides the classified into global and localized rainfall rate models [12]. experimental record only for the 1-min rainfall amount as Global rainfall rate models depend on climatic parameters discussed later in this paper. Despite the numerous models and geographical locations. In this study, we consider the proposed thus far, empirical techniques have been selected proposed global coefficient values as listed in [13], which due to its simplicity as they are all based on conversion extend global coefficients value’s application to rain rate coefficients determined by means of measured data and their conversion methods in temperate, tropical, and cold climates, simple formulation, which allows one to extend their along with the ITU-R P.837-6 [5] method. ITU-R P.837-6 applicability to more than one climatic regions. Empirical contains the software that implements the conversion of rain conversion techniques provide analytical laws expressing rate statistics with different integration times, adopted by the relationship between equiprobable rain rate values with Study Group 3 in Recommendation P.837-6, Annex 3. Of the available 1-min and T-min integrated distributions [4]. the two operational modes as recommended in the software, In this study, we test the applicability of the following Mode A is chosen for inputting data for various times and empirical conversion methods: the Segal method [18], percentage rain rate values. Similarly, the latitude and which provides a systematic approach for obtaining a longitude information of the sites along with various source specified number of rain zones in countries such
Load more

Recommended publications
  • Rainfall Decadal Change
    Sendai Symposium B1_6253 2010.04.27 Climate-driven ecosystem shifts indicated in fishery catch statistics (1968- 2009) from Korean coastal waters Sukgeun Jung, Young Shil Kang, Young-Sang Suh, Sukyung Kang and Yeong Gong Catch of blue crab (Portunus trituberculatus) in South Korea, averaged for 1983-2007 40 North Korea 110 38 100 South Korea 90 80 70 36 60 50 Current major 40 30 fishing34 ground of 20 10 blue crab 9 8 32 7 6 5 4 3 30 2 1 0.1 0.01 28 0.001 0 kg km-2 26 122 124 126 128 130 132 134 136 138 “According to NFRDI, in 2030, South Korean fishermen may not catch blue crab any more, as global warming will shift its major fishing ground to North Korean water.” Outline of talk 1. Long-term changes in Korean waters 1) Hydrographic conditions, 1968- 2) Fish community (commercial catch), 1968- 3) Zooplankton community, 1978- 4) Correlations with respect to climate and Tsushima Warm Current 2. Future works Stations of Serial Oceanographic Data NFRDI (Korea Oceanographic Data Center) 1961-2009 Linear trend of temperature change (oC) in the land and sea surface (1968-2005) 40 Sokcho 38 Chuncheon Gangneung IncheonSeoul Ulleungdo Suwon Seosan Cheongju 3 Chupungnyeong 2.8 Gunsan Pohang 2.6 36 Jeonju Daegu 2.4 2.2 Ulsan 2 Gwangju 1.8 Busan 1.6 Tongyeong Mokpo Yeosu 1.4 1.2 1 0.8 34 0.6 0.4 Jeju 0.2 Seogwipo 0 -0.2 -0.4 -0.6 -0.8 -1 -1.2 32 -1.4 -1.6 -1.8 -2 o -2.2 C -2.4 -2.6 -2.8 30 -3 124 126 128 130 132 Linear trend of DO changes (1968-2005) 40 40 40 0 m 10 m 30 m 38 38 38 36 36 36 34 34 34 1 0.93 0.87 0.8 32 32 32 0.73 0.67 0.6 0.53 30
    [Show full text]
  • Economic Value of Terminal Aerodrome Forecasts at Incheon Airport, South Korea
    sustainability Article Economic Value of Terminal Aerodrome Forecasts at Incheon Airport, South Korea In-Gyum Kim 1,* , Hye-Min Kim 1, Dae-Geun Lee 1, Byunghwan Lim 1 and Hee-Choon Lee 2 1 Planning and Finance Division, National Institute of Meteorological Sciences, Seogwipo-si 63568, Korea; [email protected] (H.-M.K.); [email protected] (D.-G.L.); [email protected] (B.L.) 2 Earthquake and Volcano Policy Division, Korea Meteorological Administration, Seoul 07062, Korea; [email protected] * Correspondence: [email protected] Abstract: Meteorological information at an arrival airport is one of the primary variables used to determine refueling of discretionary fuel. This study evaluated the economic value of terminal aerodrome forecasts (TAF), which has not been previously quantitatively analyzed in Korea. The analysis data included 374,716 international flights that arrived at Incheon airport during 2017–2019. A cost–loss model was used for the analysis, which is a methodology to evaluate forecast value by considering the cost and loss that users can expect, considering the decision-making result based on forecast utilization. The value was divided in terms of improving fuel efficiency and reducing CO2 emissions. The results of the analysis indicate that the annual average TAF value for Incheon Airport was approximately 2.2 M–20.1 M USD under two hypothetical rules of refueling of discretionary fuel. This value is up to 26.2% higher than the total budget of 16.3 M USD set for the production of aviation meteorological forecasts by the Korea Meteorological Administration (KMA). Further, it is Citation: Kim, I.-G.; Kim, H.-M.; up to 10 times greater than the 2 M USD spent on aviation meteorological information fees collected Lee, D.-G.; Lim, B.; Lee, H.-C.
    [Show full text]
  • Democratic People's Republic of Korea
    Operational Environment & Threat Analysis Volume 10, Issue 1 January - March 2019 Democratic People’s Republic of Korea APPROVED FOR PUBLIC RELEASE; DISTRIBUTION IS UNLIMITED OEE Red Diamond published by TRADOC G-2 Operational INSIDE THIS ISSUE Environment & Threat Analysis Directorate, Fort Leavenworth, KS Topic Inquiries: Democratic People’s Republic of Korea: Angela Williams (DAC), Branch Chief, Training & Support The Hermit Kingdom .............................................. 3 Jennifer Dunn (DAC), Branch Chief, Analysis & Production OE&TA Staff: North Korea Penny Mellies (DAC) Director, OE&TA Threat Actor Overview ......................................... 11 [email protected] 913-684-7920 MAJ Megan Williams MP LO Jangmadang: Development of a Black [email protected] 913-684-7944 Market-Driven Economy ...................................... 14 WO2 Rob Whalley UK LO [email protected] 913-684-7994 The Nature of The Kim Family Regime: Paula Devers (DAC) Intelligence Specialist The Guerrilla Dynasty and Gulag State .................. 18 [email protected] 913-684-7907 Laura Deatrick (CTR) Editor Challenges to Engaging North Korea’s [email protected] 913-684-7925 Keith French (CTR) Geospatial Analyst Population through Information Operations .......... 23 [email protected] 913-684-7953 North Korea’s Methods to Counter Angela Williams (DAC) Branch Chief, T&S Enemy Wet Gap Crossings .................................... 26 [email protected] 913-684-7929 John Dalbey (CTR) Military Analyst Summary of “Assessment to Collapse in [email protected] 913-684-7939 TM the DPRK: A NSI Pathways Report” ..................... 28 Jerry England (DAC) Intelligence Specialist [email protected] 913-684-7934 Previous North Korean Red Rick Garcia (CTR) Military Analyst Diamond articles ................................................
    [Show full text]
  • In South Korea
    ADVANCES IN ATMOSPHERIC SCIENCES, VOL. 26, NO. 2, 2009, 275–282 Regional Distribution of Perceived Temperatures Estimated by the Human Heat Budget Model (the Klima-Michel Model) in South Korea Jiyoung KIM∗1,KyuRangKIM1, Byoung-Cheol CHOI1,Dae-GeunLEE1, and Jeong-Sik KIM2 1National Institute of Meteorological Research, Korea Meteorological Administration, Seoul 156-720,Korea 2Korea Global Atmosphere Watch Center, Korea Meteorological Administration, Chungnam 357-961,Korea (Received 1 November 2007; revised 4 May 2008) ABSTRACT The regional distribution of perceived temperatures (PT) for 28 major weather stations in South Korea during the past 22 years (1983–2004) was investigated by employing a human heat budget model, the Klima-Michel model. The frequencies of a cold stress and a heat load by each region were compared. The sensitivity of PT in terms of the input of synoptic meteorological variables were successfully tested. Seogwipo in Jeju Island appears to be the most comfortable city in Korea. Busan also shows a high frequency in the comfortable PT range. The frequency of the thermal comfort in Seoul is similar to that of Daejeon with a relatively low frequency. In this study, inland cities like Daegu and Daejeon had very hot thermal sensations. Low frequencies of hot thermal sensations appeared in coastal cities (e.g., Busan, Incheon, and Seogwipo). Most of the 28 stations in Korea exhibited a comfort thermal sensation over 40% in its frequency, except for the mountainous regions. The frequency of a heat load is more frequent than that of a cold stress. There are no cities with very cold thermal sensations.
    [Show full text]
  • Potential Pest Status of the Formosan
    Potential pest status of the Formosan subterranean termite, Coptotermes formosanus Shiraki (Blattodea: Isoptera: Rhinotermitidae), in response to climate change in the Korean Peninsula Sang-Bin Lee1, Reina L. Tong1, Si-Hyun Kim2, Ik Gyun Im3, and Nan-Yao Su1 Abstract Climate change impacts the current and potential distribution of many insects, since temperature is often a limiting factor to where the insects can survive. The Formosan subterranean termite, Coptotermes formosanus Shiraki (Blattodea: Rhinotermitidae), has never been reported in South Korea despite its close proximity to 2 countries (China and Japan) where this economically important pest has been reported. This may be due to the average winter temperature in South Korea which is below 4 °C, the lower limit of the current distribution range of Formosan subterranean termite. However, with climate change leading to increased temperatures, South Korea may be susceptible to successful invasion by Formosan subterranean termite. The objective of this study is to estimate the future possible distribution of Formosan subterranean termite in Korea based on temperature. Climate data from Korea showed a significant increase of 2.19 °C per 100 yr in average annual temperature from 1910 to 2018. Previous and current average winter temperatures were higher than 4 °C only in Jeju, and most provinces did not exceed 4 °C, except for some southern cities such as Busan in 2000 to 2019. With the estimated rate of temperature rises, winter temperatures in Gyeongsangnam-do will exceed 4 °C starting from 2020, and Jeollanam-do will exceed 4 °C from 2060. Coupled with the statistically significant, increased annual trade between Korea and other countries (China, Japan, Taiwan, and the USA) where C.
    [Show full text]
  • For Participants Only 04/09/2015 English Only
    FOR PARTICIPANTS ONLY 04/09/2015 ENGLISH ONLY UNITED NATIONS ECONOMIC AND SOCIAL COMMISSION FOR ASIA AND THE PACIFIC United Nations Regional Cartographic Conference for Asia and the Pacific 20th Session 6 - 9 October 2015 International Convention Center Jeju (ICC Jeju) Jeju Island, Republic of Korea INFORMATION NOTE FOR PARTICIPANTS GENERAL The 20th United Nations Regional Cartographic Conference for Asia and the Pacific is scheduled to be held at the International Convention Center Jeju (ICC Jeju) Jeju Island, Republic of Korea, 2700 Jungmun, Seogwipo, Jeju Special Self-Governing Province, 697-120, Korea, from 6 – 9 October 2015. The event will be opened at 9:00 hours on Tuesday, 6 October 2015, in the International Convention Center Jeju (ICC Jeju), where all subsequent meetings will also be held from 09:00 hours to 12:00 hours and 14:00 hours to 17:00 hours. We will inform you if there is a change on this in due course. REGISTRATION AND IDENTIFICATION BADGES Participants are requested to register and obtain meeting badges at the Registration Counter, located at the Main Hall of the ICC Jeju, between 8:30 and 10:00 hours on the opening day of the event. Participants who are not able to register during the time indicated above are requested to do so upon their arrival at UNCC before going to the conference room. Only the names of duly registered participants will be included in the list of participants. VISA FREE ENTRY TO KOREA Considering international convention, mutuality doctrine, national profit and other such factors, certain countries are granted visa-free entry permissions.
    [Show full text]
  • Lee Jung-Seob 1916~1990 Brochure.Pdf
    Seoul (1954 – 1955) Daegu (1955) Jeongneung, Seoul (1956) Letter Paintings With his family still in Japan, Lee moved to Following the January 1955 exhibition in Seoul, Starting in December 1955, Lee spent time in Seoul, where he stayed with friends and acquain- Lee held another solo exhibition in April at the various hospitals, before moving to Jeongneung, In July 1952, amidst the devastation of the Korean tances in places like Nusang-dong and Sangsu- Gallery of the US Information Service in Daegu. Seoul, where he stayed in the homes of War, Lee’s wife and two sons left for Japan, dong. Around this time, Lee’s wife earned some This exhibition was organized with the help Han Mook (painter, b. 1914), Park Yeonhee leaving him alone. From that time on, he mean- money by selling Japanese books at a mark-up of Ku Sang (1919 – 2004), a poet and close friend of (novelist, 1918 – 2008), and Jo Yeongam (poet, dered between many different places, but in Korea, but a middleman swindled Lee on the Lee. However, this exhibition had even worse b. 1920). During this period, he did some no matter where he went, he regularly sent letters deal, plunging him into debt. Hoping to pay results than the one in Seoul, sending Lee into illustrations for literary magazines and created his to his family overseas. The early letters are this debt and be reunited with his family in Japan, a state of depression. Now convinced that he was ¿QDOZRUNVLQFOXGLQJWKHRiver of No Return joyful and affectionate, imbued with the hope that Lee made a last-ditch effort to sell his works deceiving the world about being an important series.
    [Show full text]
  • Let's Live a Happy Life in Korea
    You are a beloved wife. You are a respected mother. You are a wonderful daughter-in-law. You are a valuable new citizen of Korea. The Ministry for Health, Welfare and Family Affairs will be your reliable friend and we will help you plan for a brighter future in Korea. GUIDE BOOK for Married We love you. Immigrants in Korea Let’s live a happy life in Korea The Transnational Marriage & Family-Support Center (☎1577-5432) provides multicultural families with various services such as education, counseling, child care, child birth education, and cultural programs for their stable settlement and harmonious family relationships in Korea. Important telephone numbers for helping make your life easier in Korea Feel free to call when you need any help Service Center Telephone Emergency Telephone Transnational Marriage & Family- Immigrant Women Emergency 1577-5432 1577-1366 Support Center Support Center Emergencies, Special Calls, Crime Healthy Family Support Center 1577-9337 112 Report National Health Insurance Counseling 1577-1000 Fire/Health & Security 119 School Violence and Women in Employment Support Center 1588-1919 117 Let’s live Prostitution Health & Welfare Call Center 129 Child Abuse 1391 Emergency Counseling and Hospital Korea Legal and Corporation 132 1339 a happy life Information National Health Insurance Counseling 02)3270-9161 1644–0644 Interpretation Service in Korea! for Foreigners 02)3270-9338 1577-0177 Welcome to Korea. It must be difficult to live in Korea which Important telephone numbers for helping make your life easier in Korea has different language, custom, and culture Service Center Telephone Telephone Bangladesh 02)796-4056 310-22 Dongbinggo-dong Yongsan-gu Seoul compared to your homeland.
    [Show full text]
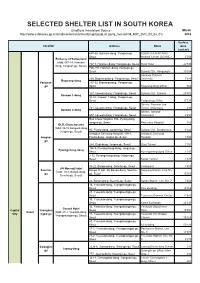
  • Selected Shelter List in South Korea
    SELECTED SHELTER LIST IN SOUTH KOREA (Unofficial translation/ Source : March http://www.safekorea.go.kr/dmtd/contents/civil/est/EmgnEqupList.jsp?q_menuid=M_NST_SVC_03_04_01) 2016 Surface Location Address Name Area SOON CHUN HYANG Medical Center, (unit:m²) 657-58, Hannam-dong, Yongsan-gu, SOON CHUN HYANG Seoul Medical Center (SCHMC) 2'056 Embassy of Switzerland (Add: 657-14, Hannam- 747-7, Hannam-dong, Yongsan-gu, Seoul Hyatt Hotel 22'539 dong, Yongsan-gu, Seoul) 726-494, Hannam-dong, Yongsan-gu, Seoul Subway Stn. Hangangjin 10'794 Hankook Politech 238, Bogwang-dong, Yongsan-gu, Seoul University 1'643 Bogwang-dong Yongsan- 217-32, Bigwang-dong, Yongsan-gu, gu Seoul Bogwang-dong Office 660 127, Itaewon-dong, Yongsan-gu, Seoul Subway Stn. Itaewon 25'572 Itaewon 1-dong 34-87, Itaewon 1-dong, Yongsan-gu, Seoul Yongsan-gu Office 17'737 Shelter, Namsan 2nd 721, Itaewon-dong, Yongsan-gu, Seoul Tunnel Underpass 439 Itaewon 2-dong Shelter, Itaewon 507, Itaewon-dong, Yongsan-gu, Seoul Underpass 2'294 Red Cross Hospital, 956, Pyung-dong, Jongno-gu, Seoul Red cross Hospital 789 OLD_Chancery area (Add: 32-10 Songwol-dong, 90, Pyung-dong, Jongno-gu, Seoul Subway Stn. Seodaemun 9'244 Jongno-gu, Seoul) Gangbuk Samsung Hospital, 108-1, Gangbuk Samsung Jongno- Pyung-dong, Jongno-gu, Seoul Hospital 1'598 gu 244, Gugi-dong, Jongno-gu, Seoul Gugi Tunnel 1'781 186-9, Pyeongchang-dong, Jongno-gu, Pyeongchang-dong Seoul Pyeongchang-dong Office 1'797 2-12, Pyeongchang-dong, Jongno-gu, Seoul Bukak Tunnel 1'838 30-22, Banpo-dong, Seocho-gu, Seoul Underpass 1'400 JW Marriott Hotel Seocho- Banpo Xi Apt, 20, Banpo-dong, Seocho- Sapyung Station, Line No.
    [Show full text]
  • Effect of Climate Change on Annual Precipitation in Korea Using Data
    atmosphere Article Effect of Climate Change on Annual Precipitation in Korea Using Data Screening Techniques and Climate Change Scenarios Ga-Kyun Lim 1 , Byung-Sik Kim 1, Byung-Hyun Lee 1 and Se-Jin Jeung 2,* 1 Department of Urban and Environmental Disaster Prevention Engineering, Kangwon National University, 346, Joongang-Ro, Samcheok-Si, Gangwon-Do 25913, Korea; [email protected] (G.-K.L.); [email protected] (B.-S.K.); [email protected] (B.-H.L.) 2 Kangwon Institute of Inclusive Technology, 1, Kangwondaehak-gil, Chuncheon-si, Gangwon-do 24341, Korea * Correspondence: [email protected]; Tel.: +82-033-570-6819 Received: 8 June 2020; Accepted: 16 September 2020; Published: 24 September 2020 Abstract: Precipitation is essential for understanding hydrological processes and identifying the characteristics that must be considered to protect human lives and property from natural disasters. Hydrological analyses assume that precipitation shows stationarity. However, because of the recent changes in climate, the stationarity of climate data has been widely debated, and a need has arisen to analyze its nonstationary nature. In this study, we reviewed a method to analyze the stationarity of annual precipitation data from 37 meteorological stations that have recorded data for more than 45 years. Six stations that showed abnormal precipitation during the previous year were selected to evaluate the normality of future precipitation. The results showed that a significant trend was present in four out of 37 stations with unstable precipitation in 22 stations and persistent precipitation in 4 stations. The stationarity analysis of future annual precipitation using climate change scenarios suggested that no trend would be present in 11 stations and that unstable precipitation would be present in six stations.
    [Show full text]
  • 大韓民国 (Republic of Korea)
    大韓民国 (Republic of Korea) 検査機関名 (Name) 検査機関住所 (Address) コード Ａ 公的検査機関 (Official laboratories) 1 Ministry of Food and Drug Safety Osong Health Technology Administration KR10001 (食品医薬品安全処） Complex, 187 Osong Saengmyeong 2-ro Osong-eup, Heungdeok-gu, Cheongju-si, Chungcheongbuk-do, Republic of Korea 2 Seoul Metropolitan Government Research 30, Janggunmaeul 3-gil, Gwacheon-si, KR10002 Institute of Public Health & Environment Gyeonggi-do, Republic of Korea (ソウル特別市 保健環境研究院） 3 Busan Metropolitan City Institute of Health & 120, Hambakbong-ro 140 beon-gil, Buk-gu, KR10003 Environment Busan. Republic of Korea (釜山廣域市 保健環境研究院) 4 Incheon Metropolitan City Institute of Health 471, Seohae-daero, Jung-gu, Incheon, KR10004 & Environment Republic of Korea (仁川廣域市 保健環境研究院) 5 Gyeonggi-Do Institute of Health & 62, Chilbo-ro 1beon-gil, Gwonseon-gu, KR10005 Environment Suwon-si, Gyeonggi-do, Republic of Korea (京畿道 保健環境研究院) 6 Gangwon Institute of Health & Environment 386-1, Sinbuk-ro, Sinbuk-eup, Chuncheon- KR10006 (江原道 保健環境研究院) si, Gangwon-do, Republic of Korea 7 Chungcheongbuk-Do Research Institute of 184, Osongsaengmyeong 1-ro, Osong-eup, KR10007 Health & Environment Heungdeok-gu, Cheongju-si, (忠清北道 保健環境研究院) Chungcheongbuk-do, Republic of Korea 8 Chungcheongnam-Do Institute of Health and 8,Hongyegongwon-ro, Hongbuk-eup, KR10008 Environment Research Hongseong-gun, Chungcheongnam-do, （忠清南道 保健環境研究院） Republic of Korea 9 Jeollabuk-Do Institute of Health and 1601, Hoguk-ro, Imsil-eup, Imsil-gun, KR10009 Environment Research Jeollabuk-do, Republic of Korea (全羅北道 保健環境研究院)
    [Show full text]
  • Allergenic Pollen Calendar in Korea Based on Probability Distribution Models and Up-To-Date Observations
    Allergy Asthma Immunol Res. 2020 Mar;12(2):259-273 https://doi.org/10.4168/aair.2020.12.2.259 pISSN 2092-7355·eISSN 2092-7363 Original Article Allergenic Pollen Calendar in Korea Based on Probability Distribution Models and Up-to-Date Observations Ju-Young Shin ,1 Mae Ja Han ,1 Changbum Cho ,1 Kyu Rang Kim ,1* Jong-Chul Ha ,1 Jae-Won Oh 2* 1Applied Meteorology Research Division, National Institute of Meteorological Sciences, Seogwipo, Korea 2Department of Pediatrics, Hanyang University Guri Hospital, Hanyang University College of Medicine, Seoul, Korea Received: Aug 12, 2019 ABSTRACT Revised: Oct 8, 2019 Accepted: Oct 21, 2019 Purpose: The pollen calendar is the simplest forecasting method for pollen concentrations. Correspondence to As pollen concentrations are liable to seasonal variations due to alterations in climate and Kyu Rang Kim, PhD land-use, it is necessary to update the pollen calendar using recent data. To attenuate the Applied Meteorology Research Division, National Institute of Meteorological Sciences, impact of considerable temporal and spatial variability in pollen concentrations on the pollen 33 Seohobuk-ro, Seogwipo 63568, Korea. calendar, it is essential to employ a new methodology for its creation. Tel: +82-64-780-6753 Methods: A pollen calendar was produced in Korea using data from recent observations, Fax: +82-64-738-6515 and a new method for creating the calendar was proposed, considering both risk levels E-mail: [email protected] and temporal resolution of pollen concentrations. A probability distribution was used for smoothing concentrations and determining risk levels. Airborne pollen grains were collected Jae-Won Oh, MD, PhD Department of Pediatrics, Hanyang University between 2007 and 2017 at 8 stations; 13 allergenic pollens, including those of alder, Japanese Guri Hospital, Hanyang University College cedar, birch, hazelnut, oak, elm, pine, ginkgo, chestnut, grasses, ragweed, mugwort and of Medicine, 153 Gyeongchun-ro, Guri 11923, Japanese hop, were identified from the collected grains.
    [Show full text]