From Deep Learning to Hyperdimensional Computing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Business Reporting on the Internet
BUSINESS REPORTING ON THE INTERNET A REPORT PREPARED FOR THE INTERNATIONAL ACCOUNTING STANDARDS COMMITTEE BY ANDREW LYMER UNIVERSITY OF BIRMINGHAM UK ROGER DEBRECENY NANYANG TECHNOLOGICAL UNIVERSITY SINGAPORE GLEN L. GRAY CALIFORNIA STATE UNIVERSITY AT NORTHRIDGE USA ASHEQ RAHMAN NANYANG TECHNOLOGICAL UNIVERSITY SINGAPORE NOVEMBER 1999 This Discussion Paper is issued by the IASC staff to stimulate thinking. The Discussion Paper has not been considered by the Board of the International Accounting Standards Committee and does not necessarily represent the views of the Board. No responsibility for loss occasioned to any person acting or refraining from action as a result of any material in this publication can be accepted by the authors or publisher. © 1999 International Accounting Standards Committee ISBN 0 905625 77 3 All rights reserved. No part of this Discussion Paper may be translated, reprinted or reproduced or utilised in any form either in whole or in part or by any electronic, mechanical or other means, now known or hereafter invented, including photocopying and recording, or in any information storage and retrieval system, without permission in writing from the International Accounting Standards Committee. The ® “Hexagon Device”, “IAS”, “IASC” and “International Accounting Standards”are registered Trade Marks of the International Accounting Standards Committee and should not be used without the approval of the International Accounting Standards Committee. International Accounting Standards Committee, 166 Fleet Street, London EC4A -
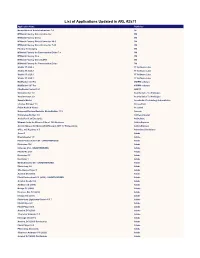
List of Applications Updated in ARL #2571
List of Applications Updated in ARL #2571 Application Name Publisher Nomad Branch Admin Extensions 7.0 1E M*Modal Fluency Direct Connector 3M M*Modal Fluency Direct 3M M*Modal Fluency Direct Connector 10.0 3M M*Modal Fluency Direct Connector 7.85 3M Fluency for Imaging 3M M*Modal Fluency for Transcription Editor 7.6 3M M*Modal Fluency Flex 3M M*Modal Fluency Direct CAPD 3M M*Modal Fluency for Transcription Editor 3M Studio 3T 2020.2 3T Software Labs Studio 3T 2020.8 3T Software Labs Studio 3T 2020.3 3T Software Labs Studio 3T 2020.7 3T Software Labs MailRaider 3.69 Pro 45RPM software MailRaider 3.67 Pro 45RPM software FineReader Server 14.1 ABBYY VoxConverter 3.0 Acarda Sales Technologies VoxConverter 2.0 Acarda Sales Technologies Sample Master Accelerated Technology Laboratories License Manager 3.5 AccessData Prizm ActiveX Viewer AccuSoft Universal Restore Bootable Media Builder 11.5 Acronis Knowledge Builder 4.0 ActiveCampaign ActivePerl 5.26 Enterprise ActiveState Ultimate Suite for Microsoft Excel 18.5 Business Add-in Express Add-in Express for Microsoft Office and .NET 7.7 Professional Add-in Express Office 365 Reporter 3.5 AdminDroid Solutions Scout 1 Adobe Dreamweaver 1.0 Adobe Flash Professional CS6 - UNAUTHORIZED Adobe Illustrator CS6 Adobe InDesign CS6 - UNAUTHORIZED Adobe Fireworks CS6 Adobe Illustrator CC Adobe Illustrator 1 Adobe Media Encoder CC - UNAUTHORIZED Adobe Photoshop 1.0 Adobe Shockwave Player 1 Adobe Acrobat DC (2015) Adobe Flash Professional CC (2015) - UNAUTHORIZED Adobe Acrobat Reader DC Adobe Audition CC (2018) -
Mind Hacking
Mind Hacking Table of Contents Introduction 0 My Story 0.1 What is Mind Hacking? 0.2 Hello World 0.3 Analyzing 1 You Are Not Your Mind 1.1 Your Mind Has a Mind of Its Own 1.2 Developing Jedi-Like Concentration 1.3 Debugging Your Mental Loops 1.4 Imagining 2 It's All in Your Mind 2.1 Your Best Possible Future 2.2 Creating Positive Thought Loops 2.3 Reprogramming 3 Write 3.1 Repeat 3.2 Simulate 3.3 Collaborate 3.4 Act 3.5 Mind Hacking Resources 4 Quick Reference 5 Endnotes 6 2 Mind Hacking Mind Hacking JOIN THE MIND HACKING MOVEMENT. Mind Hacking teaches you how to reprogram your thinking -- like reprogramming a computer -- to give you increased mental efficiency and happiness. The entire book is available here for free: Click here to start reading Mind Hacking. If you enjoy Mind Hacking, we hope you'll buy a hardcover for yourself or a friend. The book is available from Simon & Schuster's Gallery Books, and includes worksheets for the entire 21-Day plan: Click here to order Mind Hacking on Amazon.com. The best way to become a mind hacker is to download the free app, which will guide you through the 21-day plan: Click here to download the free Mind Hacking app. Sign up below, and we'll send you a series of guided audio exercises (read by the author!) that will make you a master mind hacker: Click here to get the free audio exercises. Hack hard and prosper! This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. -

Avid Unity Mediamanager Select Players V2.5.15 Readme • 0130-06356-01 Rev
a Avid Unity™ MediaManager Select Players Version 2.5.15 ReadMe Important Information Avid® recommends that you read all the information in this ReadMe file thoroughly before installing or using any new software release. Important: Search the Avid Knowledge Base for the most up-to-date ReadMe file, which contains the latest information that might have become available after the documentation was published. This document describes compatibility issues with previous releases, hardware and software requirements, supported client information, and summary information on system and memory requirements. This document also lists hardware and software limitations. Overview Use this ReadMe file to supplement the install process described in the Avid Unity MediaManager Installation and Setup Guide for the following Avid MediaManager Select Players: • MediaManager Browser Player • MediaManager ProLog Player • Avid Player n Before you can play media in any of the Players using an ethernet-attached server, you must install the MediaNetwork Ethernet® Attached Client (EAC) software. You do not need the EAC software if you have Fibre Channel attached clients. Contents If You Need Help . 3 Symbols and Conventions . 3 Features Added in v2.5.x . 4 Sending Media to a Playback Device from the ProLog Player . 4 Playing Audio Only in the ProLog Player. 6 Hardware and Software Requirements . 7 Recommended Video Cards . 9 Installation Prerequisites . 9 Supported Avid Unity ISIS Media Network . 10 Supported Avid Unity MediaNetwork. 10 Avid Unity MediaManager v4.5.16. 10 Special Notes . 11 International Character Support. 11 Supported Video and Film Formats. 11 Installing the Software . 12 Documentation Changes . 13 Accessing Online Support . 13 Fixed in v2.5.14 . -

This Week's Finds in Mathematical Physics
This Week’s Finds in Mathematical Physics Weeks 1 to 50 January 19, 1993 to March 12, 1995 by John Baez typeset by Tim Hosgood = Preface These are the first 50 issues of This Week’s Finds of Mathematical Physics. This series has sometimes been called the world’s first blog, though it was originally posted on a “usenet newsgroup” called sci.physics.research — a form of communication that predated the world-wide web. I began writing this series as a way to talk about papers I was reading and writing, and in the first 50 issues I stuck closely to this format. These issues focus rather tightly on quantum gravity, topological quantum field theory, knot theory, and applications of n-categories to these subjects. However, there are also digressions into Lie algebras, elliptic curves, linear logic and other subjects. Tim Hosgood kindly typeset all 300 issues of This Week’s Finds in 2020. They will be released in six installments of 50 issues each. I have edited the issues here to make the style a bit more uniform and also to change some references to preprints, technical reports, etc. into more useful arXiv links. This accounts for some anachronisms where I discuss a paper that only appeared on the arXiv later. I thank Blake Stacey for helping me fix many mistakes. There are undoubtedly many still remaining. If you find some, please contact me and I will try to fix them. 1 CONTENTS CONTENTS Contents Week 1 January 19, 1993............... 3 Week 26 November 21, 1993 ....... 132 Week 2 January 24, 1993.............. -

List of Section 13F Securities, Fourth Quarter 2006
List of Section 13F Securities 4th Quarter FY 2006 Copyright (c) 2007 American Bankers Association. CUSIP Numbers and descriptions are used with permission by Standard & Poors CUSIP Service Bureau, a division of The McGraw-Hill Companies, Inc. All rights reserved. No redistribution without permission from Standard & Poors CUSIP Service Bureau. Standard & Poors CUSIP Service Bureau does not guarantee the accuracy or completeness of the CUSIP Numbers and standard descriptions included herein and neither the American Bankers Association nor Standard & Poor's CUSIP Service Bureau shall be responsible for any errors, omissions or damages arising out of the use of such information. U.S. Securities and Exchange Commission OFFICIAL LIST OF SECTION 13(f) SECURITIES USER INFORMATION SHEET General This list of “Section 13(f) securities” as defined by Rule 13f-1(c) [17 CFR 240.13f-1(c)] is made available to the public pursuant to Section13 (f) (3) of the Securities Exchange Act of 1934 [15 USC 78m(f) (3)]. It is made available for use in the preparation of reports filed with the Securities and Exhange Commission pursuant to Rule 13f-1 [17 CFR 240.13f-1] under Section 13(f) of the Securities Exchange Act of 1934. An updated list is published on a quarterly basis. This list is current as of December 15, 2006, and may be relied on by institutional investment managers filing Form 13F reports for the calendar quarter ending December 31, 2006. Institutional investment managers should report holdings--number of shares and fair market value--as of the last day of the calendar quarter as required by [ Section 13(f)(1) and Rule 13f-1] thereunder. -

The Multiplayer Game: User Identity and the Meaning Of
THE MULTIPLAYER GAME: USER IDENTITY AND THE MEANING OF HOME VIDEO GAMES IN THE UNITED STATES, 1972-1994 by Kevin Donald Impellizeri A dissertation submitted to the Faculty of the University of Delaware in partial fulfilment of the requirements for the degree of Doctor of Philosophy in History Fall 2019 Copyright 2019 Kevin Donald Impellizeri All Rights Reserved THE MULTIPLAYER GAME: USER IDENTITY AND THE MEANING OF HOME VIDEO GAMES IN THE UNITED STATES, 1972-1994 by Kevin Donald Impellizeri Approved: ______________________________________________________ Alison M. Parker, Ph.D. Chair of the Department of History Approved: ______________________________________________________ John A. Pelesko, Ph.D. Dean of the College of Arts and Sciences Approved: ______________________________________________________ Douglas J. Doren, Ph.D. Interim Vice Provost for Graduate and Professional Education and Dean of the Graduate College I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: ______________________________________________________ Katherine C. Grier, Ph.D. Professor in charge of dissertation. I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: ______________________________________________________ Arwen P. Mohun, Ph.D. Member of dissertation committee I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: ______________________________________________________ Jonathan Russ, Ph.D. -

By Robert A. Lund TAMING the HP 3000
by Robert A. Lund TAMING THE HP 3000 Volume II TAMING THE HP 3000 Volumell The Theory and Practice of Successful Performance Management for Hewlett-Packard lIP 3000 Computer Systems Robert A. Lund Performance Press Publishing AJbany,Oregon 97321 TAMING THE HP 3000 - Volume II The Theory and Practice of Successful Performance Management for Hewlett-Packard HP 3000 Computer Systems Copyright (c) 1992 by Robert A. Lund Manufactured in the United States of America All rights reserved. No part of this book may be used or reproduced in any form or by any means without the prior written permission of the publisher (unless noted otherwise) except for brief quotes in connection with critical reviews written specifically for inclusion in a journal magazine, or newspaper. First edition 1992 Manuscript preparation by Performance Press, Albany, Oregon. Printing by Commercial Bindery Werks , Salem. Oregon. ISBN cr945325-02-9 (cloth) cr945325-03-7 (paper) Library of Congress card catalog number: 87-092025 First Printing 8/92 - 200 Seoond Printing 9/92-1800 NOTICE: Performance Press makes no express or implied warranty with regard to the performance managing techniques herein offered. The ideas offered are made available on an "as is" basis, and the entire risk as to their quality and performance is with the user. Should the methodologies or ideas described herein prove damaging in any way, the user (and not Performance Press, nor Robert A. Lund nor any other party) shall bear the entire cost of all necessary correction and all incidental or consequential damages. Performance Press, nor Robert A. Lund shall not be liable for errors contained herein, or any incidental or consequential damages in connection with. -

Sales Rep Account Marketing VP Hollander, Adam @Task Pontacoloni, Nick 1&1 Internet Inc. Belcher, Eric 123Together Pelino, M
Sales Rep Account Marketing VP Hollander, Adam @Task Pontacoloni, Nick 1&1 Internet Inc. Belcher, Eric 123Together Pelino, Matt 1E Hollander, Adam 21st Century Software Flynn, Shannon 24-7 InTouch Tonello, Alicia 2Wire Brian Sugar Nolan, Kevin 2X Software Ltd Tamara Borg Khan, Zemira 360DegreeWeb, Inc. Chili Sastry Hartman, Rich 3COM James L. Freeze Votta, Geoff 3e Technologies International Pelino, Matt 3i Consulting Hartman, Rich 3M Telecommunications Moon, Sarah 3Pardata, Inc Keough, Tim 3UP Systems Inc Romano, Ryan 411 Computers, Inc Gilbert, Nicole 4D Blaisdell, Elizabeth 4FrontSecurity Mullen, Lindsay 4Gen Consulting Pelino, Matt 7Irene Tonello, Jeff 8e6 Technologies Tonello, Alicia 8x8 Click, Tom A & G Software Hartman, Rich Aastra Bolduc, Michael Ab Initio Software Delanders, Richard AB&T Telecom Mullen, Lindsay Abaco Mobile Blaisdell, Elizabeth Abacus Consulting Services Mullen, Lindsay Abacus Software Romano, Ryan Abacus Solutions Mullen, Lindsay ABeam Consulting Fournier, Sarah Aberdeen LLC Keough, Tim Above All Software Votta, Geoff AboveNet Tonello, Alicia ABP Tech Connon, Katherine ABREVITY, Inc. Nolan, Kevin Abridean Inc. Delanders, Richard ABS Associates Pelino, Matt Absoft Romano, Ryan Absolute Performance Pontacoloni, Nick Absolute Software Hollander, Adam Abtech Systems Coffin, Jillian Academic Software Pelino, Matt ACAL Fcs Fix, Chris Accelerance Blaisdell, Elizabeth Accelerated Security Keough, Tim Accellion Pelino, Matt AccelTree Software Barros, Pam Accent Technologies Driscoll, David Accenture Pontacoloni, Nick -

1994 Cern School of Computing
CERN 95-01 20 January 1995 ORGANISATION EUROPÉENNE POUR LA RECHERCHE NUCLÉAIRE CERN EUROPEAN ORGANIZATION FOR NUCLEAR RESEARCH 1994 CERN SCHOOL OF COMPUTING Sopron, Hungary 28 August-10 September 1994 PROCEEDINGS Editors: CE. Vandoni, C. Verkerk GENEVA 1995 pour tous les pays du mande. Ce docu ment (K; all countries of the world. This report-, or peut être reproduit OU traduit on tout oïl en any part of it, may not be reprinted ox trans partie Sttnà l'autorisation écrite du Directeur lated without written pcrmisaion of the copy p.c:ncr»| du CEFUV, titulaire dn droit d'autour. right holder, the Director-General of CER.N. Dan» lea cas appropriés, cl s'il s'agit d'utiliser I In we via-, permission will be freely granted for le document, à dos fins non commerciales, cette appropriate non-comrnereja| use- autorisation ser* volontiers accordée. If any patentable invention or registrable Le CER.N ne revendique pad la propriété des design is described in the report, GERN makes inventions brcvetables et dessins ou modèles no claim to property rights in it but offers it susceptibles de dépôt qui pourraient elfe for the free use of research institutions, man décrits dans le présent di>cu ment; ceux-ci peu ufacturer» and others. CERN, however, mety vent être librement utilisés par les instituts de oppose any attempt by a user to C-I&iln any recherche, les industriels et autres intéireaBéfi. proprietary or patent rights in such inventions Cependant, le CERN se réserve te droit de or designs as may be described In the present s'opposer à toute revendication qu'un usager document. -

Configuration Parameters
SailPoint Version 7.3 -2 Integration Guide Copyright © 2019 SailPoint Technologies, Inc., All Rights Reserved. SailPoint Technologies, Inc. makes no warranty of any kind with regard to this manual, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose. SailPoint Technologies shall not be liable for errors contained herein or direct, indirect, special, incidental or consequential damages in connection with the furnishing, performance, or use of this material. Restricted Rights Legend. All rights are reserved. No part of this document may be published, distributed, reproduced, publicly displayed, used to create derivative works, or translated to another language, without the prior written consent of SailPoint Technologies. The information contained in this document is subject to change without notice. Use, duplication or disclosure by the U.S. Government is subject to restrictions as set forth in subparagraph (c) (1) (ii) of the Rights in Technical Data and Computer Software clause at DFARS 252.227-7013 for DOD agencies, and subparagraphs (c) (1) and (c) (2) of the Commercial Computer Software Restricted Rights clause at FAR 52.227-19 for other agencies. Regulatory/Export Compliance. The export and re-export of this software is controlled for export purposes by the U.S. Government. By accepting this software and/or documentation, licensee agrees to comply with all U.S. and foreign export laws and regulations as they relate to software and related documentation. Licensee will not export or re-export outside the United States software or documentation, whether directly or indirectly, to any Prohibited Party and will not cause, approve or otherwise intentionally facilitate others in so doing. -

Final Version of Technical White Paper
Big Data Technical Working Groups White Paper BIG 318062 Project Acronym: BIG Project Title: Big Data Public Private Forum (BIG) Project Number: 318062 Instrument: CSA Thematic Priority: ICT-2011.4.4 D2.2.2 Final Version of Technical White Paper Work Package: WP2 Strategy & Operations Due Date: 28/02/2014 Submission Date: 14/05/2014 Start Date of Project: 01/09/2012 Duration of Project: 26 Months Organisation Responsible of Deliverable: NUIG Version: 1.0 Status: Final Author name(s): Edward Curry (NUIG) Panayotis Kikiras (AGT), Andre Freitas (NUIG) John Domingue (STIR) Andreas Thalhammer (UIBK) Nelia Lasierra (UIBK) Anna Fensel (UIBK) Marcus Nitzschke (INFAI) Axel Ngonga (INFAI) Michael Martin (INFAI) Ivan Ermilov (INFAI) Mohamed Morsey (INFAI) Klaus Lyko (INFAI) Philipp Frischmuth (INFAI) Martin Strohbach (AGT) Sarven Capadisli (INFAI) Herman Ravkin (AGT) Sebastian Hellmann (INFAI) Mario Lischka (AGT) Tilman Becker (DFKI) Jörg Daubert (AGT) Tim van Kasteren (AGT) Amrapali Zaveri (INFAI) Umair Ul Hassan (NUIG) Reviewer(s): Amar Djalil Mezaour Helen Lippell (PA) (EXALEAD) Marcus Nitzschke (INFAI) Axel Ngonga (INFAI) Michael Hausenblas (NUIG) Klaus Lyko (INFAI) Tim Van Kasteren (AGT) Nature: R – Report P – Prototype D – Demonstrator O - Other Dissemination level: PU - Public CO - Confidential, only for members of the consortium (including the Commission) RE - Restricted to a group specified by the consortium (including the Commission Services) Project co-funded by the European Commission within the Seventh Framework Programme (2007-2013)