Control Complexity in Bucklin and Fallback Voting: a Theoretical Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Influences in Voting and Growing Networks
UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Influences in Voting and Growing Networks Permalink https://escholarship.org/uc/item/0fk1x7zx Author Racz, Miklos Zoltan Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Statistics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Elchanan Mossel, Chair Professor James W. Pitman Professor Allan M. Sly Professor David S. Ahn Spring 2015 Influences in Voting and Growing Networks Copyright 2015 by Mikl´osZolt´anR´acz 1 Abstract Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz Doctor of Philosophy in Statistics University of California, Berkeley Professor Elchanan Mossel, Chair This thesis studies problems in applied probability using combinatorial techniques. The first part of the thesis focuses on voting, and studies the average-case behavior of voting systems with respect to manipulation of their outcome by voters. Many results in the field of voting are negative; in particular, Gibbard and Satterthwaite showed that no reasonable voting system can be strategyproof (a.k.a. nonmanipulable). We prove a quantitative version of this result, showing that the probability of manipulation is nonnegligible, unless the voting system is close to being a dictatorship. We also study manipulation by a coalition of voters, and show that the transition from being powerless to having absolute power is smooth. These results suggest that manipulation is easy on average for reasonable voting systems, and thus computational complexity cannot hide manipulations completely. -
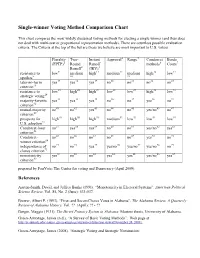
Single-Winner Voting Method Comparison Chart
Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama. -

Ranked-Choice Voting from a Partisan Perspective
Ranked-Choice Voting From a Partisan Perspective Jack Santucci December 21, 2020 Revised December 22, 2020 Abstract Ranked-choice voting (RCV) has come to mean a range of electoral systems. Broadly, they can facilitate (a) majority winners in single-seat districts, (b) majority rule with minority representation in multi-seat districts, or (c) majority sweeps in multi-seat districts. Such systems can be combined with other rules that encourage/discourage slate voting. This paper describes five major versions used in U.S. public elections: Al- ternative Vote (AV), single transferable vote (STV), block-preferential voting (BPV), the bottoms-up system, and AV with numbered posts. It then considers each from the perspective of a `political operative.' Simple models of voting (one with two parties, another with three) draw attention to real-world strategic issues: effects on minority representation, importance of party cues, and reasons for the political operative to care about how voters rank choices. Unsurprisingly, different rules produce different outcomes with the same votes. Specific problems from the operative's perspective are: majority reversal, serving two masters, and undisciplined third-party voters (e.g., `pure' independents). Some of these stem from well-known phenomena, e.g., ballot exhaus- tion/ranking truncation and inter-coalition \vote leakage." The paper also alludes to vote-management tactics, i.e., rationing nominations and ensuring even distributions of first-choice votes. Illustrative examples come from American history and comparative politics. (209 words.) Keywords: Alternative Vote, ballot exhaustion, block-preferential voting, bottoms- up system, exhaustive-preferential system, instant runoff voting, ranked-choice voting, sequential ranked-choice voting, single transferable vote, strategic coordination (10 keywords). -

Präferenzaggregation Durch Wählen: Algorithmik Und Komplexität
Pr¨aferenzaggregationdurch W¨ahlen: Algorithmik und Komplexit¨at Folien zur Vorlesung Wintersemester 2017/2018 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU D¨usseldorf) Pr¨aferenzaggregation durch W¨ahlen 1 / 57 Preliminary Remarks Websites Websites Vorlesungswebsite: http:==ccc:cs:uni-duesseldorf:de=~rothe=wahlen Anmeldung im LSF J. Rothe (HHU D¨usseldorf) Pr¨aferenzaggregation durch W¨ahlen 2 / 57 Preliminary Remarks Literature Literature J. Rothe (Herausgeber): Economics and Computation: An Introduction to Algorithmic Game Theory, Computational Social Choice, and Fair Division. Springer-Verlag, 2015 with a preface by Matt O. Jackson und Yoav Shoham (Stanford) Buchblock 155 x 235 mm Abstand 6 mm Springer Texts in Business and Economics Rothe Springer Texts in Business and Economics Jörg Rothe Editor Economics and Computation Ed. An Introduction to Algorithmic Game Theory, Computational Social Choice, and Fair Division J. Rothe D. Baumeister C. Lindner I. Rothe This textbook connects three vibrant areas at the interface between economics and computer science: algorithmic game theory, computational social choice, and fair divi- sion. It thus offers an interdisciplinary treatment of collective decision making from an economic and computational perspective. Part I introduces to algorithmic game theory, focusing on both noncooperative and cooperative game theory. Part II introduces to Jörg Rothe Einführung in computational social choice, focusing on both preference aggregation (voting) and judgment aggregation. Part III introduces to fair division, focusing on the division of Editor Computational Social Choice both a single divisible resource ("cake-cutting") and multiple indivisible and unshare- able resources ("multiagent resource allocation"). In all these parts, much weight is Individuelle Strategien und kollektive given to the algorithmic and complexity-theoretic aspects of problems arising in these areas, and the interconnections between the three parts are of central interest. -

Group Decision Making with Partial Preferences
Group Decision Making with Partial Preferences by Tyler Lu A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Computer Science University of Toronto c Copyright 2015 by Tyler Lu Abstract Group Decision Making with Partial Preferences Tyler Lu Doctor of Philosophy Graduate Department of Computer Science University of Toronto 2015 Group decision making is of fundamental importance in all aspects of a modern society. Many commonly studied decision procedures require that agents provide full preference information. This requirement imposes significant cognitive and time burdens on agents, increases communication overhead, and infringes agent privacy. As a result, specifying full preferences is one of the contributing factors for the limited real-world adoption of some commonly studied voting rules. In this dissertation, we introduce a framework consisting of new concepts, algorithms, and theoretical results to provide a sound foundation on which we can address these problems by being able to make group decisions with only partial preference information. In particular, we focus on single and multi-winner voting. We introduce minimax regret (MMR), a group decision-criterion for partial preferences, which quantifies the loss in social welfare of chosen alternative(s) compared to the unknown, but true winning alternative(s). We develop polynomial-time algorithms for the computation of MMR for a number of common of voting rules, and prove intractability results for other rules. We address preference elicitation, the second part of our framework, which concerns the extraction of only the relevant agent preferences that reduce MMR. We develop a few elicitation strategies, based on common ideas, for different voting rules and query types. -

Voting with Rank Dependent Scoring Rules
Voting with Rank Dependent Scoring Rules Judy Goldsmith, Jer´ omeˆ Lang, Nicholas Mattei, and Patrice Perny Abstract Positional scoring rules in voting compute the score of an alternative by summing the scores for the alternative induced by every vote. This summation principle ensures that all votes con- tribute equally to the score of an alternative. We relax this assumption and, instead, aggregate scores by taking into account the rank of a score in the ordered list of scores obtained from the votes. This defines a new family of voting rules, rank-dependent scoring rules (RDSRs), based on ordered weighted average (OWA) operators, which include all scoring rules, and many oth- ers, most of which of new. We study some properties of these rules, and show, empirically, that certain RDSRs are less manipulable than Borda voting, across a variety of statistical cultures and on real world data from skating competitions. 1 Introduction Voting rules aim at aggregating the ordinal preferences of a set of individuals in order to produce a commonly chosen alternative. Many voting rules are defined in the following way: given a vot- ing profile P, a collection of votes, where a vote is a linear ranking over alternatives, each vote contributes to the score of an alternative. The global score of the alternative is then computed by summing up all these contributed (“local”) scores, and finally, the alternative(s) with the highest score win(s). The most common subclass of these scoring rules is that of positional scoring rules: the local score of x with respect to vote v depends only on the rank of x in v, and the global score of x is the sum, over all votes, of its local scores. -

Math 105 Workbook Exploring Mathematics
Math 105 Workbook Exploring Mathematics Douglas R. Anderson, Professor Fall 2018: MWF 11:50-1:00, ISC 101 Acknowledgment First we would like to thank all of our former Math 105 students. Their successes, struggles, and suggestions have shaped how we teach this course in many important ways. We also want to thank our departmental colleagues and several Concordia math- ematics majors for many fruitful discussions and resources on the content of this course and the makeup of this workbook. Some of the topics, examples, and exercises in this workbook are drawn from other works. Most significantly, we thank Samantha Briggs, Ellen Kramer, and Dr. Jessie Lenarz for their work in Exploring Mathematics, as well as other Cobber mathemat- ics professors. We have also used: • Taxicab Geometry: An Adventure in Non-Euclidean Geometry by Eugene F. Krause, • Excursions in Modern Mathematics, Sixth Edition, by Peter Tannenbaum. • Introductory Graph Theory by Gary Chartrand, • The Heart of Mathematics: An invitation to effective thinking by Edward B. Burger and Michael Starbird, • Applied Finite Mathematics by Edmond C. Tomastik. Finally, we want to thank (in advance) you, our current students. Your suggestions for this course and this workbook are always encouraged, either in person or over e-mail. Both the course and workbook are works in progress that will continue to improve each semester with your help. Let's have a great semester this fall exploring mathematics together and fulfilling Concordia's math requirement in 2018. Skol Cobbs! i ii Contents 1 Taxicab Geometry 3 1.1 Taxicab Distance . .3 Homework . .8 1.2 Taxicab Circles . -

The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity 3
Working Paper The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity Haris Aziz · Barton E. Lee Abstract Proportional representation (PR) is often discussed in voting settings as a major desideratum. For the past century or so, it is common both in practice and in the academic literature to jump to single transferable vote (STV) as the solution for achieving PR. Some of the most prominent electoral reform movements around the globe are pushing for the adoption of STV. It has been termed a major open prob- lem to design a voting rule that satisfies the same PR properties as STV and better monotonicity properties. In this paper, we first present a taxonomy of proportional representation axioms for general weak order preferences, some of which generalise and strengthen previously introduced concepts. We then present a rule called Expand- ing Approvals Rule (EAR) that satisfies properties stronger than the central PR axiom satisfied by STV, can handle indifferences in a convenient and computationally effi- cient manner, and also satisfies better candidate monotonicity properties. In view of this, our proposed rule seems to be a compelling solution for achieving proportional representation in voting settings. Keywords committee selection · multiwinner voting · proportional representation · single transferable vote. JEL Classification: C70 · D61 · D71 1 Introduction Of all modes in which a national representation can possibly be constituted, this one [STV] affords the best security for the intellectual qualifications de- sirable in the representatives—John Stuart Mill (Considerations on Represen- tative Government, 1861). arXiv:1708.07580v2 [cs.GT] 4 Jun 2018 H. Aziz · B. E. Lee Data61, CSIRO and UNSW, Sydney 2052 , Australia Tel.: +61-2-8306 0490 Fax: +61-2-8306 0405 E-mail: [email protected], [email protected] 2 Haris Aziz, Barton E. -

Voting Systems: from Method to Algorithm
Voting Systems: From Method to Algorithm A Thesis Presented to The Faculty of the Com puter Science Department California State University Channel Islands In (Partial) Fulfillment of the Requirements for the Degree M asters of Science in Com puter Science b y Christopher R . Devlin Advisor: Michael Soltys December 2019 © 2019 Christopher R. Devlin ALL RIGHTS RESERVED APPROVED FOR MS IN COMPUTER SCIENCE Advisor: Dr. Michael Soltys Date Name: Dr. Bahareh Abbasi Date Name: Dr. Vida Vakilian Date APPROVED FOR THE UNIVERITY Name Date Acknowledgements I’d like to thank my wife, Eden Byrne for her patience and support while I completed this Masters Degree. I’d also like to thank Dr. Michael Soltys for his guidance and mentorship. Additionally I’d like to thank the faculty and my fellow students at CSUCI who have given nothing but assistance and encouragement during my time here. Voting Systems: From Method to Algorithm Christopher R. Devlin December 18, 2019 Abstract Voting and choice aggregation are used widely not just in poli tics but in business decision making processes and other areas such as competitive bidding procurement. Stakeholders and others who rely on these systems require them to be fast, efficient, and, most impor tantly, fair. The focus of this thesis is to illustrate the complexities inherent in voting systems. The algorithms intrinsic in several voting systems are made explicit as a way to simplify choices among these systems. The systematic evaluation of the algorithms associated with choice aggregation will provide a groundwork for future research and the implementation of these tools across public and private spheres. -
![Control Complexity in Bucklin, Fallback, and Plurality Voting: an Experimental Approach Arxiv:1203.3967V2 [Cs.GT] 20 Aug 2012](https://docslib.b-cdn.net/cover/6154/control-complexity-in-bucklin-fallback-and-plurality-voting-an-experimental-approach-arxiv-1203-3967v2-cs-gt-20-aug-2012-3086154.webp)
Control Complexity in Bucklin, Fallback, and Plurality Voting: an Experimental Approach Arxiv:1203.3967V2 [Cs.GT] 20 Aug 2012
Control Complexity in Bucklin, Fallback, and Plurality Voting: An Experimental Approach∗ Jorg¨ Rothe and Lena Schend Institut fur¨ Informatik Heinrich-Heine-Universitat¨ Dusseldorf¨ 40225 Dusseldorf,¨ Germany September 12, 2018 Walsh [Wal10, Wal09], Davies et al. [DKNW10, DKNW11], and Narodytska et al. [NWX11] studied various voting systems empirically and showed that they can often be manipulated ef- fectively, despite their manipulation problems being NP-hard. Such an experimental approach is sorely missing for NP-hard control problems, where control refers to attempts to tamper with the outcome of elections by adding/deleting/partitioning either voters or candidates. We ex- perimentally tackle NP-hard control problems for Bucklin and fallback voting. Among natural voting systems with efficient winner determination, fallback voting is currently known to display the broadest resistance to control in terms of NP-hardness, and Bucklin voting has been shown to behave almost as well in terms of control resistance [ER10, EPR11, EFPR11]. We also in- vestigate control resistance experimentally for plurality voting, one of the first voting systems analyzed with respect to electoral control [BTT92, HHR07]. Our findings indicate that NP-hard control problems can often be solved effectively in prac- tice. Moreover, our experiments allow a more fine-grained analysis and comparison—across various control scenarios, vote distribution models, and voting systems—than merely stating NP-hardness for all these control problems. arXiv:1203.3967v2 [cs.GT] 20 Aug 2012 ∗This work was supported in part by DFG grants RO 1202/15-1 and RO 1202/12-1 (within the EUROCORES programme LogICCC of the ESF), SFF grant “Cooperative Normsetting” of HHU Dusseldorf,¨ and a DAAD grant for a PPP project in the PROCOPE programme. -

Why Approval Voting Is Unworkable in Contested Elections
Why Approval Voting is Unworkable in Contested Elections And How the Borda Count, Score Voting, Range Voting and Bucklin Voting are Similarly Flawed Due to Vulnerability to Strategic Voting An Analysis by FairVote, July 2011 Summary Approval voting is a method of voting to elect single winners that has adherents among some voting theorists, but is unworkable in contested elections in which voters have a stake in the outcome. Once aware of how approval voting works, strategic voters will always earn a significant advantage over less informed voters. This problem with strategic voting far outweighs any other factor when evaluating the potential use of approval voting in governmental elections. Among other methods that should not be used in meaningfully contested elections are range voting, score voting, the Borda Count and Bucklin voting. They all share approval voting’s practical flaw of not allowing voters to support a second choice without potentially causing the defeat of their first choice. Such voting methods have their potential value, but only in elections where voters have no particular stake in the outcome. The only voting methods that should be weighed seriously for governmental elections are methods that do not violate this “later-no-harm” criterion (plurality voting and forms of runoff elections and instant runoff voting [http://www.instantrunoff.com] ) or only do so indirectly (such as Condorcet voting methods). We support our claims about approval voting and similar voting methods both with theoretical analysis and with a broad range of evidence, including the failure of these voting methods in every single significant use in meaningfully contested elections. -

Comparing Bucklin Voting to Ranked Choice Voting and Approval Voting an Analysis for the City and County of Denver January 2020
Comparing Bucklin Voting to Ranked Choice Voting and Approval Voting An Analysis for the City and County of Denver January 2020 This report differentiates between three entirely separate voting methods. According to Arrow’s Impossibility Theorem, no mathematically perfect voting method exists. Thus, public administrators look to political scientists to aid in identifying best practices. Why is Bucklin Voting significant? Among the alternative voting methods that have been tried, but failed is Bucklin Voting (BV). The Bucklin ballot uses rankings, so it is tempting to confuse it with Ranked Choice Voting (RCV). However, BV’s tally makes it less like RCV and more like Approval Voting (AV). HISTORIC & LEGAL OVERVIEW.. Bucklin Voting was first proposed by Marquis de Condorcet in 1793, and later implemented by James W. Bucklin in Grand Junction, CO in 1909. It is sometimes called the Grand Junction Method. It was eventually used in 60+ cities including Denver & San Francisco. The courts struck it down in Minnesota and Oklahoma; Brown vs. Smallwood (1915) found that it provided more than one vote per voter. Other places including Denver repealed it because it is susceptible to strategic voting. Ranked Choice Voting is the voter-centered name for a system invented for proportional representation in multi-winner elections in the 1850's. It was later adapted for implementation in single-winner races by William Ware of MIT in the 1870’s. RCV is sometimes called Single Transferable Vote when used in multiple-winner races and is sometimes called Instant Runoff Voting when used in single-winner races. RCV was first implemented in the US in Ashtabula, Ohio in 1915.