Units in Electricity and Magnetism
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Representation of Derived Units in Unitsml (Revised December 8, 2006)
Representation of Derived Units in UnitsML (revised December 8, 2006) Peter J. Linstrom∗ December 8, 2006 ∗phone: (301) 975-5422,DRAFT e-mail: [email protected] 1 INTRODUCTION 12/8/06 Contents 1 Introduction 1 2 Why this convention is needed 2 3 Information needed to define a unit 3 4 Proposed XML encoding 4 5 Important conventions 7 6 Potential problems 8 7 Possible alternatives 10 A Multiplicative prefixes 12 B SI units and units acceptable for use with the SI 14 C non-SI Units 19 1 Introduction This document describes a proposed convention for defining derived units in terms of their base units. This convention is intended for use in the UnitsML markup language to allow a precise definition of a wide range of units. The goal of this convention is to improve interoperability among applications and databases which use derived units based on commonly encountered base units. It is understoodDRAFT that not all units can be represented using this convention. It is, however, Representation of Derived Units in UnitsML (revised December 8, 2006) Page 1 2 WHY THIS CONVENTION IS NEEDED 12/8/06 anticipated that a wide range of scientific and engineering units of measure can be represented with this convention. The convention consists of representing the unit in terms of multiplicative combinations of base units. For example the unit centimeter per second squared would be represented in terms of the following: 1. The unit meter with the prefix centi raised to the power 1. 2. The unit second raised to the power −2. -

Astm Metric Practice Guide
National Bureau of Standards Library, E-01 Admrn. Bldg. A111DO cmfl4S - m 2 0 1967 METRIC PRACTICE GUIDE NATL INST OF STANDARDS & TECH R.I.C. All100991845 /NBS handbook QC1 .U51 V102;1967 C.1 NBS-PUB-C 1934 U. S. DEPARTMENT OF COMMERCE NATIONAL OUREAU OF STANDARDS HANDBOOK 102 THE NATIONAL BUREAU OF STANDARDS The National Bureau of Standards 1 provides measurement and technical information services essential to the efficiency and effectiveness of the work of the Nation’s scientists and engineers. The Bureau serves also as a focal point in the Federal Government for assuring maximum application of the physical and engineering sciences to the advancement of technology in industry and commerce. To accomplish this mission, the Bureau is organized into three institutes covering broad program areas of research and services: THE INSTITUTE FOR BASIC STANDARDS . provides the central basis within the United States for a complete and consistent system of physical measurements, coordinates that system with the measurement systems of other nations, and furnishes essential services leading to accurate and uniform physical measurements throughout the Nation’s scientific com¬ munity, industry, and commerce. This Institute comprises a series of divisions, each serving a classical subject matter area: —Applied Mathematics — Electricity—Metrology — Mechanics — Heat — Atomic Physics—Physical Chemistry—Radiation Physics—Laboratory Astrophysics2—Radio Standards Laboratory,2 which includes Radio Standards Physics and Radio Standards Engineering—Office of Standard Reference Data. THE INSTITUTE FOR MATERIALS RESEARCH . conducts materials research and provides associated materials services including mainly reference materials and data on the properties of materials. Beyond its direct interest to the Nation’s scientists and engineers, this Institute yields services which are essential to the advancement of technology in industry and commerce. -

On the First Electromagnetic Measurement of the Velocity of Light by Wilhelm Weber and Rudolf Kohlrausch
Andre Koch Torres Assis On the First Electromagnetic Measurement of the Velocity of Light by Wilhelm Weber and Rudolf Kohlrausch Abstract The electrostatic, electrodynamic and electromagnetic systems of units utilized during last century by Ampère, Gauss, Weber, Maxwell and all the others are analyzed. It is shown how the constant c was introduced in physics by Weber's force of 1846. It is shown that it has the unit of velocity and is the ratio of the electromagnetic and electrostatic units of charge. Weber and Kohlrausch's experiment of 1855 to determine c is quoted, emphasizing that they were the first to measure this quantity and obtained the same value as that of light velocity in vacuum. It is shown how Kirchhoff in 1857 and Weber (1857-64) independently of one another obtained the fact that an electromagnetic signal propagates at light velocity along a thin wire of negligible resistivity. They obtained the telegraphy equation utilizing Weber’s action at a distance force. This was accomplished before the development of Maxwell’s electromagnetic theory of light and before Heaviside’s work. 1. Introduction In this work the introduction of the constant c in electromagnetism by Wilhelm Weber in 1846 is analyzed. It is the ratio of electromagnetic and electrostatic units of charge, one of the most fundamental constants of nature. The meaning of this constant is discussed, the first measurement performed by Weber and Kohlrausch in 1855, and the derivation of the telegraphy equation by Kirchhoff and Weber in 1857. Initially the basic systems of units utilized during last century for describing electromagnetic quantities is presented, along with a short review of Weber’s electrodynamics. -

Electric Units and Standards
DEPARTMENT OF COMMERCE OF THE Bureau of Standards S. W. STRATTON, Director No. 60 ELECTRIC UNITS AND STANDARDS list Edition 1 Issued September 25. 1916 WASHINGTON GOVERNMENT PRINTING OFFICE DEPARTMENT OF COMMERCE Circular OF THE Bureau of Standards S. W. STRATTON, Director No. 60 ELECTRIC UNITS AND STANDARDS [1st Edition] Issued September 25, 1916 WASHINGTON GOVERNMENT PRINTING OFFICE 1916 ADDITIONAL COPIES OF THIS PUBLICATION MAY BE PROCURED FROM THE SUPERINTENDENT OF DOCUMENTS GOVERNMENT PRINTING OFFICE WASHINGTON, D. C. AT 15 CENTS PER COPY A complete list of the Bureau’s publications may be obtained free of charge on application to the Bureau of Standards, Washington, D. C. ELECTRIC UNITS AND STANDARDS CONTENTS Page I. The systems of units 4 1. Units and standards in general 4 2. The electrostatic and electromagnetic systems 8 () The numerically different systems of units 12 () Gaussian systems, and ratios of the units 13 “ ’ (c) Practical ’ electromagnetic units 15 3. The international electric units 16 II. Evolution of present system of concrete standards 18 1. Early electric standards 18 2. Basis of present laws 22 3. Progress since 1893 24 III. Units and standards of the principal electric quantities 29 1. Resistance 29 () International ohm 29 Definition 29 Mercury standards 30 Secondary standards 31 () Resistance standards in practice 31 (c) Absolute ohm 32 2. Current 33 (a) International ampere 33 Definition 34 The silver voltameter 35 ( b ) Resistance standards used in current measurement 36 (c) Absolute ampere 37 3. Electromotive force 38 (a) International volt 38 Definition 39 Weston normal cell 39 (b) Portable Weston cells 41 (c) Absolute and semiabsolute volt 42 4. -

Alexander Graham Bell 1847-1922
NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF AMERICA BIOGRAPHICAL MEMOIRS VOLUME XXIII FIRST MEMOIR BIOGRAPHICAL MEMOIR OF ALEXANDER GRAHAM BELL 1847-1922 BY HAROLD S. OSBORNE PRESENTED TO THE ACADEMY AT THE ANNUAL MEETING, 1943 It was the intention that this Biographical Memoir would be written jointly by the present author and the late Dr. Bancroft Gherardi. The scope of the memoir and plan of work were laid out in cooperation with him, but Dr. Gherardi's untimely death prevented the proposed collaboration in writing the text. The author expresses his appreciation also of the help of members of the Bell family, particularly Dr. Gilbert Grosvenor, and of Mr. R. T. Barrett and Mr. A. M. Dowling of the American Telephone & Telegraph Company staff. The courtesy of these gentlemen has included, in addition to other help, making available to the author historic documents relating to the life of Alexander Graham Bell in the files of the National Geographic Society and in the Historical Museum of the American Telephone and Telegraph Company. ALEXANDER GRAHAM BELL 1847-1922 BY HAROLD S. OSBORNE Alexander Graham Bell—teacher, scientist, inventor, gentle- man—was one whose life was devoted to the benefit of mankind with unusual success. Known throughout the world as the inventor of the telephone, he made also other inventions and scientific discoveries of first importance, greatly advanced the methods and practices for teaching the deaf and came to be admired and loved throughout the world for his accuracy of thought and expression, his rigid code of honor, punctilious courtesy, and unfailing generosity in helping others. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

SI and CGS Units in Electromagnetism
SI and CGS Units in Electromagnetism Jim Napolitano January 7, 2010 These notes are meant to accompany the course Electromagnetic Theory for the Spring 2010 term at RPI. The course will use CGS units, as does our textbook Classical Electro- dynamics, 2nd Ed. by Hans Ohanian. Up to this point, however, most students have used the International System of Units (SI, also known as MKSA) for mechanics, electricity and magnetism. (I believe it is easy to argue that CGS is more appropriate for teaching elec- tromagnetism to physics students.) These notes are meant to smooth the transition, and to augment the discussion in Appendix 2 of your textbook. The base units1 for mechanics in SI are the meter, kilogram, and second (i.e. \MKS") whereas in CGS they are the centimeter, gram, and second. Conversion between these base units and all the derived units are quite simply given by an appropriate power of 10. For electromagnetism, SI adds a new base unit, the Ampere (\A"). This leads to a world of complications when converting between SI and CGS. Many of these complications are philosophical, but this note does not discuss such issues. For a good, if a bit flippant, on- line discussion see http://info.ee.surrey.ac.uk/Workshop/advice/coils/unit systems/; for a more scholarly article, see \On Electric and Magnetic Units and Dimensions", by R. T. Birge, The American Physics Teacher, 2(1934)41. Electromagnetism: A Preview Electricity and magnetism are not separate phenomena. They are different manifestations of the same phenomenon, called electromagnetism. One requires the application of special relativity to see how electricity and magnetism are united. -

DIMENSIONS and UNITS to Get the Value of a Quantity in Gaussian Units, Multiply the Value Ex- Pressed in SI Units by the Conversion Factor
DIMENSIONS AND UNITS To get the value of a quantity in Gaussian units, multiply the value ex- pressed in SI units by the conversion factor. Multiples of 3 intheconversion factors result from approximating the speed of light c =2.9979 1010 cm/sec × 3 1010 cm/sec. ≈ × Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units t2q2 Capacitance C l farad 9 1011 cm ml2 × m1/2l3/2 Charge q q coulomb 3 109 statcoulomb t × q m1/2 Charge ρ coulomb 3 103 statcoulomb 3 3/2 density l l t /m3 × /cm3 tq2 l Conductance siemens 9 1011 cm/sec ml2 t × 2 tq 1 9 1 Conductivity σ siemens 9 10 sec− 3 ml t /m × q m1/2l3/2 Current I,i ampere 3 109 statampere t t2 × q m1/2 Current J, j ampere 3 105 statampere 2 1/2 2 density l t l t /m2 × /cm2 m m 3 3 3 Density ρ kg/m 10− g/cm l3 l3 q m1/2 Displacement D coulomb 12π 105 statcoulomb l2 l1/2t /m2 × /cm2 1/2 ml m 1 4 Electric field E volt/m 10− statvolt/cm t2q l1/2t 3 × 2 1/2 1/2 ml m l 1 2 Electro- , volt 10− statvolt 2 motance EmfE t q t 3 × ml2 ml2 Energy U, W joule 107 erg t2 t2 m m Energy w, ϵ joule/m3 10 erg/cm3 2 2 density lt lt 10 Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units ml ml Force F newton 105 dyne t2 t2 1 1 Frequency f, ν hertz 1 hertz t t 2 ml t 1 11 Impedance Z ohm 10− sec/cm tq2 l 9 × 2 2 ml t 1 11 2 Inductance L henry 10− sec /cm q2 l 9 × Length l l l meter (m) 102 centimeter (cm) 1/2 q m 3 Magnetic H ampere– 4π 10− oersted 1/2 intensity lt l t turn/m × ml2 m1/2l3/2 Magnetic flux Φ weber 108 maxwell tq t m m1/2 Magnetic -
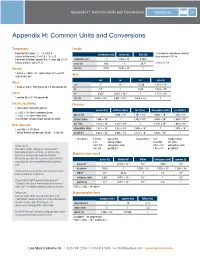
Appendix H: Common Units and Conversions Appendices 215
Appendix H: Common Units and Conversions Appendices 215 Appendix H: Common Units and Conversions Temperature Length Fahrenheit to Celsius: °C = (°F-32)/1.8 1 micrometer (sometimes referred centimeter (cm) meter (m) inch (in) Celsius to Fahrenheit: °F = (1.8 × °C) + 32 to as micron) = 10-6 m Fahrenheit to Kelvin: convert °F to °C, then add 273.15 centimeter (cm) 1 1.000 × 10–2 0.3937 -3 Celsius to Kelvin: add 273.15 meter (m) 100 1 39.37 1 mil = 10 in Volume inch (in) 2.540 2.540 × 10–2 1 –3 3 1 liter (l) = 1.000 × 10 cubic meters (m ) = 61.02 Area cubic inches (in3) cm2 m2 in2 circ mil Mass cm2 1 10–4 0.1550 1.974 × 105 1 kilogram (kg) = 1000 grams (g) = 2.205 pounds (lb) m2 104 1 1550 1.974 × 109 Force in2 6.452 6.452 × 10–4 1 1.273 × 106 1 newton (N) = 0.2248 pounds (lb) circ mil 5.067 × 10–6 5.067 × 10–10 7.854 × 10–7 1 Electric resistivity Pressure 1 micro-ohm-centimeter (µΩ·cm) pascal (Pa) millibar (mbar) torr (Torr) atmosphere (atm) psi (lbf/in2) = 1.000 × 10–6 ohm-centimeter (Ω·cm) –2 –3 –6 –4 = 1.000 × 10–8 ohm-meter (Ω·m) pascal (Pa) 1 1.000 × 10 7.501 × 10 9.868 × 10 1.450 × 10 = 6.015 ohm-circular mil per foot (Ω·circ mil/ft) millibar (mbar) 1.000 × 102 1 7.502 × 10–1 9.868 × 10–4 1.450 × 10–2 2 0 –3 –2 Heat flow rate torr (Torr) 1.333 × 10 1.333 × 10 1 1.316 × 10 1.934 × 10 5 3 2 1 1 watt (W) = 3.413 Btu/h atmosphere (atm) 1.013 × 10 1.013 × 10 7.600 × 10 1 1.470 × 10 1 British thermal unit per hour (Btu/h) = 0.2930 W psi (lbf/in2) 6.897 × 103 6.895 × 101 5.172 × 101 6.850 × 10–2 1 1 torr (Torr) = 133.332 pascal (Pa) 1 pascal (Pa) = 0.01 millibar (mbar) 1.33 millibar (mbar) 0.007501 torr (Torr) –6 A Note on SI 0.001316 atmosphere (atm) 9.87 × 10 atmosphere (atm) 2 –4 2 The values in this catalog are expressed in 0.01934 psi (lbf/in ) 1.45 × 10 psi (lbf/in ) International System of Units, or SI (from the Magnetic induction B French Le Système International d’Unités). -

Electricity and Magnetism
Lecture 10 Fundamentals of Physics Phys 120, Fall 2015 Electricity and Magnetism A. J. Wagner North Dakota State University, Fargo, ND 58102 Fargo, September 24, 2015 Overview • Unexplained phenomena • Charges and electric forces revealed • Currents and circuits • Electricity and Magnetism are related! 1 Newton’s dream I wish we could derive the rest of the phenomena of Nature by the same kind of reasoning from mechanical principles, for I am induced by many reasons to suspect that they may all depend upon certain forces by which the particles of bodies, by some cause hitherto unknown, are either mutually impelled towards one another, and cohere in regular figures, or are repelled and recede from one another. from the preface of Newton’s Principia 2 What were those mysterious phenomena? 900 BC: Magnus, a Greek shepherd, walks across a field of black stones which pull the iron nails out of his sandals and the iron tip from his shepherd’s staff (authenticity not guaranteed). This region becomes known as Magnesia. 600 BC: Thales of Miletos(Greece) discovered that by rubbing an ’elektron’ (a hard, fossilized resin that today is known as amber) against a fur cloth, it would attract particles of straw and feathers. This strange effect remained a mystery for over 2000 years. 1269 AD: Petrus Peregrinus of Picardy, Italy, discovers that natural spherical magnets (lodestones) align needles with lines of longitude pointing between two pole positions on the stone. 3 ca. 1600: Dr.William Gilbert (court physician to Queen Elizabeth) discovers that the earth is a giant magnet just like one of the stones of Peregrinus, explaining how compasses work. -

20 Coulomb's Law Of
Coulomb’s Law of 20 Electrostatic Forces Charge Interactions Are Described by Coulomb’s Law Electrical interactions between charges govern much of physics, chemistry, and biology. They are the basis for chemical bonding, weak and strong. Salts dis- solve in water to form the solutions of charged ions that cover three-quarters of the Earth’s surface. Salt water forms the working fluid of living cells. pH and salts regulate the associations of proteins, DNA, cells, and colloids, and the conformations of biopolymers. Nervous systems would not function without ion fluxes. Electrostatic interactions are also important in batteries, corrosion, and electroplating. Charge interactions obey Coulomb’s law. When more than two charged par- ticles interact, the energies are sums of Coulombic interactions. To calculate such sums, we introduce the concepts of the electric field, Gauss’s law, and the electrostatic potential. With these tools, you can determine the electrostatic force exerted by one charged object on another, as when an ion interacts with a protein, DNA molecule, or membrane, or when a charged polymer changes conformation. Coulomb’s law was discovered in careful experiments by H Cavendish (1731–1810), J Priestley (1733–1804), and CA Coulomb (1736–1806) on macro- scopic objects such as magnets, glass rods, charged spheres, and silk cloths. Coulomb’s law applies to a wide range of size scales, including atoms, molecules, and biological cells. It states that the interaction energy u(r ) 385 between two charges in a vacuum is Cq q u(r ) = 1 2 , (20.1) r where q1 and q2 are the magnitudes of the two charges, r is the distance sep- arating them, and C = 1/4πε0 is a proportionality constant (see box below). -

Manual of Style
Manual Of Style 1 MANUAL OF STYLE TABLE OF CONTENTS CHAPTER 1 GENERAL PROVISIONS ...............3 101.0 Scope .............................................. 3 102.0 Codes and Standards..................... 3 103.0 Code Division.................................. 3 104.0 Table of Contents ........................... 4 CHAPTER 2 ADMINISTRATION .........................6 201.0 Administration ................................. 6 202.0 Chapter 2 Definitions ...................... 6 203.0 Referenced Standards Table ......... 6 204.0 Individual Chapter Administrative Text ......................... 6 205.0 Appendices ..................................... 7 206.0 Installation Standards ..................... 7 207.0 Extract Guidelines .......................... 7 208.0 Index ............................................... 9 CHAPTER 3 TECHNICAL STYLE .................... 10 301.0 Technical Style ............................. 10 302.0 Technical Rules ............................ 10 Table 302.3 Possible Unenforceable and Vague Terms ................................ 10 303.0 Health and Safety ........................ 11 304.0 Rules for Mandatory Documents .................................... 11 305.0 Writing Mandatory Requirements ............................... 12 Table 305.0 Typical Mandatory Terms............. 12 CHAPTER 4 EDITORIAL STYLE ..................... 14 401.0 Editorial Style ................................ 14 402.0 Definitions ...................................... 14 403.0 Units of Measure ............................ 15 404.0 Punctuation