Mkdir / MD Command :- This Command Is Used to Create the Directory in the Dos
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
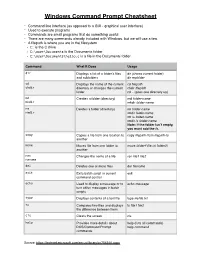
Windows Command Prompt Cheatsheet
Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx. -

Powerview Command Reference
PowerView Command Reference TRACE32 Online Help TRACE32 Directory TRACE32 Index TRACE32 Documents ...................................................................................................................... PowerView User Interface ............................................................................................................ PowerView Command Reference .............................................................................................1 History ...................................................................................................................................... 12 ABORT ...................................................................................................................................... 13 ABORT Abort driver program 13 AREA ........................................................................................................................................ 14 AREA Message windows 14 AREA.CLEAR Clear area 15 AREA.CLOSE Close output file 15 AREA.Create Create or modify message area 16 AREA.Delete Delete message area 17 AREA.List Display a detailed list off all message areas 18 AREA.OPEN Open output file 20 AREA.PIPE Redirect area to stdout 21 AREA.RESet Reset areas 21 AREA.SAVE Save AREA window contents to file 21 AREA.Select Select area 22 AREA.STDERR Redirect area to stderr 23 AREA.STDOUT Redirect area to stdout 23 AREA.view Display message area in AREA window 24 AutoSTOre .............................................................................................................................. -

Command Window – Basic Commands
Command Window – Simple Commands help lists all commands p: switch to your P-drive c: switch to the computer’s C-drive dir list all files in a directory (aka “folder”); e.g. dir (list all files in current directory) dir myfolder (list all files in subdirectory myfolder) cd change directory; e.g. cd myfolder (move to subdirectory myfolder) cd .. (move up one directory level) md make (create) a directory; e.g. md myfolder (make a subdirectory called myfolder) copy copy files; e.g. copy oldfile newfile copy source.f90 myfolder\source.f90 ren rename files; e.g. ren oldfile newfile erase erase (delete) a file; e.g. (or del) erase unwanted.txt fc file compare; e.g. fc file1 file2 type list the contents of a file type somefile.txt type somefile.txt ¦ more (list contents, one page at a time) Wildcards (* and ?) Can be used to match length-unspecified strings (*) or individual letters (?); e.g. copy *.f90 *.bak dir solve.f?? Command Syntax and Options Most commands have various options; e.g. dir /p – list files, one page at a time To find the syntax and options available for any particular command use the /? option; e.g. dir /? History Use the and arrows on keyboard to recover previous commands. Use F7 to get a list of previous commands and arrow up and down to choose one to reissue. Editors An editor called notepad comes with the operating system: notepad myfile.f90 Running Programs You can run any program simply by typing its name; e.g. to run windows explorer: explorer Batch Files To avoid having to type a long sequence of commands it is convenient to put them all in a batch file – identified by the .bat extension. -

What Is UNIX? the Directory Structure Basic Commands Find
What is UNIX? UNIX is an operating system like Windows on our computers. By operating system, we mean the suite of programs which make the computer work. It is a stable, multi-user, multi-tasking system for servers, desktops and laptops. The Directory Structure All the files are grouped together in the directory structure. The file-system is arranged in a hierarchical structure, like an inverted tree. The top of the hierarchy is traditionally called root (written as a slash / ) Basic commands When you first login, your current working directory is your home directory. In UNIX (.) means the current directory and (..) means the parent of the current directory. find command The find command is used to locate files on a Unix or Linux system. find will search any set of directories you specify for files that match the supplied search criteria. The syntax looks like this: find where-to-look criteria what-to-do All arguments to find are optional, and there are defaults for all parts. where-to-look defaults to . (that is, the current working directory), criteria defaults to none (that is, select all files), and what-to-do (known as the find action) defaults to ‑print (that is, display the names of found files to standard output). Examples: find . –name *.txt (finds all the files ending with txt in current directory and subdirectories) find . -mtime 1 (find all the files modified exact 1 day) find . -mtime -1 (find all the files modified less than 1 day) find . -mtime +1 (find all the files modified more than 1 day) find . -

MS-DOS Basics.Pdf
MS-DOS Basics The Command Prompt When you first turn on your computer, you will see some cryptic information flash by. MS-DOS displays this information to let you know how it is configuring your computer. You can ignore it for now. When the information stops scrolling past, you'll see the following: C:\> This is called the command prompt or DOS prompt. The flashing underscore next to the command prompt is called the cursor. The cursor shows where the command you type will appear. Type the following command at the command prompt: ver The following message appears on your screen: MS-DOS version 6.22 Viewing the Contents of a Directory To view the contents of a directory 1. Type the following at the command prompt: dir A list similar to the following appears: Changing Directories To change from the root directory to the WINDOWS directory To change directories, you will use the cd command. The cd command stands for "change directory." 1. Type the following at the command prompt: cd windows The command prompt changes. It should now look like the following: C:\WINDOWS> Next, you will use the dir command to view a list of the files in the DOS directory. Viewing the Contents of WINDOWS Directory To view a list of the files in the WINDOWS directory 1. Type the following at the command prompt: dir Changing Back to the Root Directory To change to the root directory 1. Type the following at the command prompt: cd \ Note that the slash you type in this command is a backslash (\), not a forward slash (/). -

CS101 Lecture 8
What is a program? What is a “Window Manager” ? What is a “GUI” ? How do you navigate the Unix directory tree? What is a wildcard? Readings: See CCSO’s Unix pages and 8-2 Applications Unix Engineering Workstations UNIX- operating system / C- programming language / Matlab Facilitate machine independent program development Computer program(software): a sequence of instructions that tells the computer what to do. A program takes raw data as input and produces information as output. System Software: • Operating Systems Unix,Windows,MacOS,VM/CMS,... • Editor Programs gedit, pico, vi Applications Software: • Translators and Interpreters gcc--gnu c compiler matlab – interpreter • User created Programs!!! 8-4 X-windows-a Window Manager and GUI(Graphical User Interface) Click Applications and follow the menus or click on an icon to run a program. Click Terminal to produce a command line interface. When the following slides refer to Unix commands it is assumed that these are entered on the command line that begins with the symbol “>” (prompt symbol). Data, information, computer instructions, etc. are saved in secondary storage (auxiliary storage) in files. Files are collected or organized in directories. Each user on a multi-user system has his/her own home directory. In Unix users and system administrators organize files and directories in a hierarchical tree. secondary storage Home Directory When a user first logs in on a computer, the user will be “in” the users home directory. To find the name of the directory type > pwd (this is an acronym for print working directory) So the user is in the directory “gambill” The string “/home/gambill” is called a path. -

Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke
Trees Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke Department of Computer Science & Engineering University of Nebraska|Lincoln Lincoln, NE 68588, USA [email protected] http://cse.unl.edu/~cbourke 2015/01/31 21:05:31 Abstract These are lecture notes used in CSCE 156 (Computer Science II), CSCE 235 (Dis- crete Structures) and CSCE 310 (Data Structures & Algorithms) at the University of Nebraska|Lincoln. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License 1 Contents I Trees4 1 Introduction4 2 Definitions & Terminology5 3 Tree Traversal7 3.1 Preorder Traversal................................7 3.2 Inorder Traversal.................................7 3.3 Postorder Traversal................................7 3.4 Breadth-First Search Traversal..........................8 3.5 Implementations & Data Structures.......................8 3.5.1 Preorder Implementations........................8 3.5.2 Inorder Implementation.........................9 3.5.3 Postorder Implementation........................ 10 3.5.4 BFS Implementation........................... 12 3.5.5 Tree Walk Implementations....................... 12 3.6 Operations..................................... 12 4 Binary Search Trees 14 4.1 Basic Operations................................. 15 5 Balanced Binary Search Trees 17 5.1 2-3 Trees...................................... 17 5.2 AVL Trees..................................... 17 5.3 Red-Black Trees.................................. 19 6 Optimal Binary Search Trees 19 7 Heaps 19 -

UNIX (Solaris/Linux) Quick Reference Card Logging in Directory Commands at the Login: Prompt, Enter Your Username
UNIX (Solaris/Linux) QUICK REFERENCE CARD Logging In Directory Commands At the Login: prompt, enter your username. At the Password: prompt, enter ls Lists files in current directory your system password. Linux is case-sensitive, so enter upper and lower case ls -l Long listing of files letters as required for your username, password and commands. ls -a List all files, including hidden files ls -lat Long listing of all files sorted by last Exiting or Logging Out modification time. ls wcp List all files matching the wildcard Enter logout and press <Enter> or type <Ctrl>-D. pattern Changing your Password ls dn List files in the directory dn tree List files in tree format Type passwd at the command prompt. Type in your old password, then your new cd dn Change current directory to dn password, then re-enter your new password for verification. If the new password cd pub Changes to subdirectory “pub” is verified, your password will be changed. Many systems age passwords; this cd .. Changes to next higher level directory forces users to change their passwords at predetermined intervals. (previous directory) cd / Changes to the root directory Changing your MS Network Password cd Changes to the users home directory cd /usr/xx Changes to the subdirectory “xx” in the Some servers maintain a second password exclusively for use with Microsoft windows directory “usr” networking, allowing you to mount your home directory as a Network Drive. mkdir dn Makes a new directory named dn Type smbpasswd at the command prompt. Type in your old SMB passwword, rmdir dn Removes the directory dn (the then your new password, then re-enter your new password for verification. -

System Analysis and Tuning Guide System Analysis and Tuning Guide SUSE Linux Enterprise Server 15 SP1
SUSE Linux Enterprise Server 15 SP1 System Analysis and Tuning Guide System Analysis and Tuning Guide SUSE Linux Enterprise Server 15 SP1 An administrator's guide for problem detection, resolution and optimization. Find how to inspect and optimize your system by means of monitoring tools and how to eciently manage resources. Also contains an overview of common problems and solutions and of additional help and documentation resources. Publication Date: September 24, 2021 SUSE LLC 1800 South Novell Place Provo, UT 84606 USA https://documentation.suse.com Copyright © 2006– 2021 SUSE LLC and contributors. All rights reserved. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or (at your option) version 1.3; with the Invariant Section being this copyright notice and license. A copy of the license version 1.2 is included in the section entitled “GNU Free Documentation License”. For SUSE trademarks, see https://www.suse.com/company/legal/ . All other third-party trademarks are the property of their respective owners. Trademark symbols (®, ™ etc.) denote trademarks of SUSE and its aliates. Asterisks (*) denote third-party trademarks. All information found in this book has been compiled with utmost attention to detail. However, this does not guarantee complete accuracy. Neither SUSE LLC, its aliates, the authors nor the translators shall be held liable for possible errors or the consequences thereof. Contents About This Guide xii 1 Available Documentation xiii -

Windows Command Line?
Table of contents 1. Why an ebook on the Windows Command Line? 2. Make an example directory 3. A little exercise: open the Windows Command Prompt window and go to the example directory 3.1 The prompt 3.2 Moving into a (sub)directory 4. Pattern-matching 5. Command ‘DIR’ and Glob patterns 6. The ‘COPY’ command and Glob patterns 6.1 Copy files from the current directory into a subdirectory 6.2 Copy files from the current directory into a subdirectory in binary mode 6.3 Combine ASCII-files and put the result into a subdirectory 6.4 Combine binary files and put the result into a subdirectory 6.5 Are the files copied correctly? 6.6 Copy a selection of files with the ‘FOR’ loop 7. The ‘DEL’ command and Glob patterns 7.1 Delete files from the current directory 7.2 Delete files from the subdirectory ‘my Doc’ -1 7.3 Delete files from the subdirectory ‘my Doc’ -2 7.3.1 An alternative 7.3.2 ROBOCOPY 8. Passing multiple commands 9. The ‘REN’ or ‘RENAME’ command 9.1 Change subdirectory name 9.2 Change file extensions 9.3 Modify filenames from the current directory: basic examples 9.4 Truncate a filename by using ‘?’ 9.5 Modify filenames in the subdirectory ‘my Doc’: basic example 10. More complex replacements 10.1 Add a prefix to filenames with the same characters at the beginning 10.2 Add a prefix to filenames with the same extensions 10.3 Add a suffix at the end of filenames with the same extensions 10.4 Substitute a character in a specific position 11. -

Command Line Interface (Shell)
Command Line Interface (Shell) 1 Organization of a computer system users applications graphical user shell interface (GUI) operating system hardware (or software acting like hardware: “virtual machine”) 2 Organization of a computer system Easier to use; users applications Not so easy to program with, interactive actions automate (click, drag, tap, …) graphical user shell interface (GUI) system calls operating system hardware (or software acting like hardware: “virtual machine”) 3 Organization of a computer system Easier to program users applications with and automate; Not so convenient to use (maybe) typed commands graphical user shell interface (GUI) system calls operating system hardware (or software acting like hardware: “virtual machine”) 4 Organization of a computer system users applications this class graphical user shell interface (GUI) operating system hardware (or software acting like hardware: “virtual machine”) 5 What is a Command Line Interface? • Interface: Means it is a way to interact with the Operating System. 6 What is a Command Line Interface? • Interface: Means it is a way to interact with the Operating System. • Command Line: Means you interact with it through typing commands at the keyboard. 7 What is a Command Line Interface? • Interface: Means it is a way to interact with the Operating System. • Command Line: Means you interact with it through typing commands at the keyboard. So a Command Line Interface (or a shell) is a program that lets you interact with the Operating System via the keyboard. 8 Why Use a Command Line Interface? A. In the old days, there was no choice 9 Why Use a Command Line Interface? A. -

Computer Graphics and Imaging UC Berkeley CS184/284A, Spring 2017 3D Transforms 3D Transformations
Lecture 5: Transforms (Cont) Computer Graphics and Imaging UC Berkeley CS184/284A, Spring 2017 3D Transforms 3D Transformations Use homogeneous coordinates again: • 3D point = (x, y, z, 1)T • 3D vector = (x, y, z, 0)T Use 4×4 matrices for affine transformations x abctx x y deft y ⇥ = y⇥ ⇥ z ghitz · z ⇧ 1 ⌃ ⇧000 1⌃ ⇧1⌃ ⇧ ⌃ ⇧ ⌃ ⇧ ⌃ ⇤ ⌅ ⇤ ⌅ ⇤ ⌅ CS184/284A Ren Ng 3D Transformations sx 000 Scale 0 sy 00 S(sx,sy,sz)= ⇥ 00sz 0 ⇧ 0001⌃ ⇧ ⌃ ⇤ ⌅ Translation 100tx 010ty T(tx,ty,tz)= ⇥ 001tz ⇧000 1⌃ ⇧ ⌃ ⇤ ⌅ Coordinate Change (Frame-to-world) uvwo F(u, v, w, o)= 0001 CS184/284A Ren Ng 3D Transformations Rotation around x-, y-, or z-axis y Rotation 10 0 0 around 0 cos α sin α 0 x-axis R (α)= x 0 sin α −cos α 0⇥ x ⇧00 0 1⌃ ⇧ ⌃ ⇤ ⌅ cos α 0 sin α 0 0100z R (α)= y sin α 0 cos α 0⇥ − ⇧ 0001⌃ ⇧ ⌃ ⇤ ⌅ cos α sin α 00 sin α −cos α 00 R (α)= z 0010⇥ ⇧ 0001⌃ ⇧ ⌃ CS184/284A ⇤ ⌅ Ren Ng 3D Rotations Compose any 3D rotation from Rx, Ry, Rz? Rxyz(α, ⇥, ⇤)=Rx(α) Ry(⇥) Rz(⇤) • So-called Euler angles • Often used in flight simulators: roll, pitch, yaw CS184/284A Ren Ng 3D Rotations Compose any 3D rotation from Rx, Ry, Rz? Rxyz(α, ⇥, ⇤)=Rx(α) Ry(⇥) Rz(⇤) • So-called Euler angles • Often used in flight simulators: roll, pitch, yaw • Problem: Gimbal Lock! CS184/284A Ren Ng f(x)=T (S (x)) f(x)=S (T (x)) 3,1 0.5 −− 0.5 3,1 f(x)=g(x)+b Euclidean: f(x)=T3,1(S0.5(x)) f(x)=S0.5(Tf3(,x1)(x))f(y) = x y −− | − | | − | f(x)=g(x)+b f(x)=R⇡/4S[1.5,1.5]x f(x)=T3,1(S0.5(x)) f(x)=S0.5(T3,1(x)) Euclidean: −−x = 22 f(x) f(y) = x y f(x)=g(x)+b | − | | − | x = ⇥0.51⇤ Euclidean: f(x)=R⇡/4S[1.5,1.5]x