DOCSLIB.ORG

Computer Graphics and Imaging UC Berkeley CS184/284A, Spring 2017 3D Transforms 3D Transformations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computer Graphics and Imaging UC Berkeley CS184/284A, Spring 2017 3D Transforms 3D Transformations Lecture 5: Transforms (Cont) Computer Graphics and Imaging UC Berkeley CS184/284A, Spring 2017 3D Transforms 3D Transformations Use homogeneous coordinates again: • 3D point = (x, y, z, 1)T • 3D vector = (x, y, z, 0)T Use 4×4 matrices for affine transformations x abctx x y deft y ⇥ = y⇥ ⇥ z ghitz · z ⇧ 1 ⌃ ⇧000 1⌃ ⇧1⌃ ⇧ ⌃ ⇧ ⌃ ⇧ ⌃ ⇤ ⌅ ⇤ ⌅ ⇤ ⌅ CS184/284A Ren Ng 3D Transformations sx 000 Scale 0 sy 00 S(sx,sy,sz)= ⇥ 00sz 0 ⇧ 0001⌃ ⇧ ⌃ ⇤ ⌅ Translation 100tx 010ty T(tx,ty,tz)= ⇥ 001tz ⇧000 1⌃ ⇧ ⌃ ⇤ ⌅ Coordinate Change (Frame-to-world) uvwo F(u, v, w, o)= 0001 CS184/284A Ren Ng 3D Transformations Rotation around x-, y-, or z-axis y Rotation 10 0 0 around 0 cos α sin α 0 x-axis R (α)= x 0 sin α −cos α 0⇥ x ⇧00 0 1⌃ ⇧ ⌃ ⇤ ⌅ cos α 0 sin α 0 0100z R (α)= y sin α 0 cos α 0⇥ − ⇧ 0001⌃ ⇧ ⌃ ⇤ ⌅ cos α sin α 00 sin α −cos α 00 R (α)= z 0010⇥ ⇧ 0001⌃ ⇧ ⌃ CS184/284A ⇤ ⌅ Ren Ng 3D Rotations Compose any 3D rotation from Rx, Ry, Rz? Rxyz(α, ⇥, ⇤)=Rx(α) Ry(⇥) Rz(⇤) • So-called Euler angles • Often used in flight simulators: roll, pitch, yaw CS184/284A Ren Ng 3D Rotations Compose any 3D rotation from Rx, Ry, Rz? Rxyz(α, ⇥, ⇤)=Rx(α) Ry(⇥) Rz(⇤) • So-called Euler angles • Often used in flight simulators: roll, pitch, yaw • Problem: Gimbal Lock! CS184/284A Ren Ng f(x)=T (S (x)) f(x)=S (T (x)) 3,1 0.5 −− 0.5 3,1 f(x)=g(x)+b Euclidean: f(x)=T3,1(S0.5(x)) f(x)=S0.5(Tf3(,x1)(x))f(y) = x y −− | − | | − | f(x)=g(x)+b f(x)=R⇡/4S[1.5,1.5]x f(x)=T3,1(S0.5(x)) f(x)=S0.5(T3,1(x)) Euclidean: −−x = 22 f(x) f(y) = x y f(x)=g(x)+b | − | | − | x = ⇥0.51⇤ Euclidean: f(x)=R⇡/4S[1.5,1.5]x f(x) f(xy=) ⇥=e2 +x e3⇤y x = 22 | − | | − | f(x)=xR⇡=2/4Se[11.5+2,1.5]ex2 x = ⇥0.51⇤ 3D Rotation Around Arbitrary Axisx =x =220.51 x =⇥e + e ⇤ 2 3 e ⇥ e ⇤ x = ⇥0.511 −⇤ 2 x =2e +2e Rotations arbitrary: 1 2 y Construct orthonormal frame x =⇥e2 + e3⇤ x = 0.51 u v w x =2e1−+2e−2 transformation F with p, u, v, w, 1 T e1⇥ e2 ⇤ R− = R − x = 0.51 where p and w match the rotation axis u u u Rotations arbitrary: x y z R e=1⇥ ev2 ⇤xv v u v w uvw −2 x y z 3 − − p w w w Rotations arbitrary: x y z -1 ux uy uz 4 5 Apply the transform (F Rz(θ) FR ) = v v v Ruuvwvu =w100 uvw 2 x yz z 3 − − w w w 1 T x y z RRuvw− v==R⇥010⇤ 4 5 ux uy uz Ruvww = ⇥001⇤ R = v v v Interpretations (both valid): uvw 2 x y z 3 wx w⇥y uxwz vx⇤ wx 1 T Ruvw− = R4 uvw = uy 5vy wy • Move to Z axis, rotate, then move back Ruvwu = 1002 3 uz vx wz 4 5 • Cast w-axis rotation in new coordinate frameRuvwv = ⇥010⇤ Ruvww = ⇥001⇤ CS184/284A Ren⇥ uNgx vx⇤ wx 1 T R− = R = u v w uvw uvw 2 y y y3 uz vx wz 4 5 4 4 4 Rodrigues’ Rotation Formula Rotation by angle α around axis n 0 nz ny T − R(n, α) = cos(α) I + (1 cos(α)) nn + sin(α) nz 0 nx − −n n 0 ⇥ y − x ⇤ N ⌅ ⌥ ⌃⇧ How to prove this magic formula? • Matrix N computes a cross-product: N x = n × x • Assume orthonormal system e1, e2, n Rn = n Re1 = cos α e1 + sin α e2 Re2 = sin α e1 + cos α e2 CS184/284A − Ren Ng Many Other Representations of Rotations Quaternions Exponential map … CS184/284A Ren Ng Hierarchical Transforms Skeleton - Linear Representation head torso right upper arm right lower arm right hand left upper arm left lower arm left hand right upper leg right lower leg right foot left upper leg left lower leg left foot CS184/284A Ren Ng Linear Representation Each shape associated with its own transform A single edit can require updating many transforms • E.g. raising arm requires updating transforms for all arm parts CS184/284A Ren Ng Skeleton - Hierarchical Representation torso head right arm upper arm lower arm hand left arm upper arm lower arm hand right leg upper leg lower leg foot left leg upper leg lower leg foot CS184/284A Ren Ng Hierarchical Representation Grouped representation (tree) • Each group contains subgroups and/or shapes • Each group is associated with a transform relative to parent group • Transform on leaf-node shape is concatenation of all transforms on path from root node to leaf • Changing a group’s transform affects all parts • Allows high level editing by changing only one node • E.g. raising left arm requires changing only one transform for that group CS184/284A Ren Ng Skeleton - Hierarchical Representation translate(0, 10); drawTorso(); pushmatrix(); // push a copy of transform onto stack translate(0, 5); // right-multiply onto current transform rotate(headRotation); // right-multiply onto current transform drawHead(); popmatrix(); // pop current transform off stack pushmatrix(); translate(-2, 3); rotate(rightShoulderRotation); drawUpperArm(); pushmatrix(); translate(0, -3); rotate(elbowRotation); drawLowerArm(); pushmatrix(); right translate(0, -3); lower right rotate(wristRotation); right arm arm drawHand(); hand group popmatrix(); group popmatrix(); popmatrix(); …. CS184/284A Ren Ng Skeleton - Hierarchical Representation translate(0, 10); drawTorso(); pushmatrix(); // push a copy of transform onto stack translate(0, 5); // right-multiply onto current transform rotate(headRotation); // right-multiply onto current transform drawHead(); popmatrix(); // pop current transform off stack pushmatrix(); translate(-2, 3); rotate(rightShoulderRotation); drawUpperArm(); pushmatrix(); translate(0, -3); rotate(elbowRotation); drawLowerArm(); pushmatrix(); right translate(0, -3); lower right rotate(wristRotation); right arm arm drawHand(); hand group popmatrix(); group popmatrix(); popmatrix(); …. CS184/284A Ren Ng Viewing and Perspective “Standard” Camera Space y z We will use this convention for “standard” camera coordinates: • camera located at the origin looking down negative z-axis x • • vertical vector is y-axis • (x-axis) orthogonal to y & z CS184/284A Ren Ng “Standard” Camera Coordinates y y z x x Resulting image (z-axis pointing away from scene) CS184/284A Ren Ng Consider A Camera Pointing in The World CS184/284A Ren Ng Consider A Camera Pointing in The World u = up vector v = view direction e = eye point (position of camera) CS184/284A Ren Ng Camera “Look-At” Transformation u = up vector v = view direction e = eye point (position of camera) Input: e, u & v given in world space coordinates Output: transform matrix from world space CS184/284Ato standard camera space Ren Ng Camera “Look-At” Transformation Inverse: Matrix from standard camera to world space (Why? This is a coordinate frame transform to (e,r,u,-v)) r u v e x x − x x ry uy vy ey r u −v e ⇥ z z − z z ⇧ 00 0 1⌃ ⇧ ⌃ ⇤ ⌅ “Look-at” transform is the inverse of above matrix: 1 rx ux vx ex − rx ry rz 0 100 ex r u −v e u u u 0 010−e y y − y y⇥ = x y z ⇥ − y⇥ rz uz vz ez vx vy vz 0 · 001 ez − − − − − ⇧ 00 0 1⌃ ⇧ 0001⌃ ⇧000 1⌃ ⇧ ⌃ ⇧ ⌃ ⇧ ⌃ ⇤ ⌅ ⇤ ⌅ ⇤ ⌅ CS184/284A Ren Ng Viewing Perspective Orthographic CS184/284A Ren Ng Perspective Projection Credit: jefflynchphoto.com Perspective in Art CS184/284A Ren Ng Perspective in Art CS184/284A Giotto 1290 Ren Ng Perspective in Art CS184/284A Giotto 1290 Ren Ng Perspective in Art Brunelleschi experiment c. 1413 Perspective in Art Delivery of the Keys (Sistine Chapel), Perugino, 1482 Perspective in Art The Last Supper, Leonardo da Vinci, 1499 Pinhole Camera (Camera Obscura) Mo Tzu (c. 470–c. 390 BC) Aristotle (384–322 BC) Ibn al-Haytham (965–1040) Shen Kuo (1031–1095) Roger Bacon (c. 1214–1294) Johannes Kepler (1571–1630) A. H. Zewail, Phil. Trans. R. Soc. A 2010;368:1191-1204 CS184/284A Ren Ng Pinhole Camera (Camera Obscura) CS184/284A Ren Ng Projective Transforms x, y (x, y, z)T Scene point -z Image C point d Inverted image (as in real pinhole camera) CS184/284A Ren Ng Projective Transforms x, y (x, y, z)T Image point Scene point -z C d Upright image CS184/284A Ren Ng Projective Transforms Standard perspective projection • Center of projection: (0, 0, 0)T • Image plane at z = d x, y (x,y,z)T x d/z x · x d/z y 0y d/z1 ⇠= · 0 1 7! · y d/z! C z d · -z B C @ A @ A z = d CS184/284A Ren Ng Projective Transforms Standard perspective projection x d/z x · • Center of projection: (0, 0, 0)T y y d/z 0 1 7! 0 · 1 z d • Image plane at z = d B C @ A @ A Perspective foreshortening • Need division by z • Matrix representation? ➡Homogeneous coordinates! CS184/284A Ren Ng Homogenous Coordinates (3D) wx x 10 0 0 wy y 01 0 0 p = M = 0 1 0wz1 0z1 00 1 0 B w C B1C B001/d 0C B C B C B C @ A @ A @ A x x xd/z y y yd/z q = M = 0z1 0 z 1 0 d 1 B1C Bz/dC B 1 C B C B C B C @ A @ A @ A CS184/284A Ren Ng Perspective Projection From Angel and Shreiner, Interactive Computer Graphics CS184/284A Ren Ng Perspective Projection (1, 1, 1) (right, top, –near) (left, bottom, –near) z = –far z = –near (–1, –1, –1) Camera Coordinates Normalized Device Coords “NDC” CS184/284A Later we will “flatten” NDC to get screen coordinates Ren Ng Perspective Transform Matrix near right 00 0right near 0 top 00top P = 2 far+near 2far near 3 2 3 00 − ⇤ near − far near far near − 6 00 −10− 7 6 1 7 6 − 7 6 7 4 near 5 4 5 near = 2 far+near 2far near 3 near ⇤ ⇤ far near − far near 6 −near − 7 6 7 CS184/284A4 1 5 Ren Ng 1 = 2 far+near 3 −far near 6 −1 7 6 7 4 1 5 1 = 2 13 − 6 1 7 6 7 4 5 Perspective Transform Matrix Example near near right right0000 0 0right right near near 0 top0 top 0000top top P = 2P = 2 far+nearfar+near2far near2far3 2near 3 23 3 0000 − ⇤ − ⇤ near near − far near− far nearfar nearfar near− − 6 006 00−10−10− −7 6 17 67 1 7 6 6 − − 7 6 7 67 7 4 4near near 5 4 5 45 5 near near = 2 = 2 far+nearfar+near2far near2far3 near 3 near near ⇤ ⇤ ⇤ far near⇤ far−nearfar −nearfar near 6 6 −near −near− 7− 7 6 6 7 7 4 14 1 5 5 1 1 = 2 far= +2nearfar3+near 3 −far near−far near 6 −16 7−1 7 6 6 7 7 4 1 4 1 5 5 1 1 = = 2 13 2 13 − − 6 1 7 6 1 7 6 7 6 7 4 5 4 5 CS184/284A Ren Ng Specifying Perspective Projection From Angel and Shreiner, Interactive Computer Graphics CS184/284A Ren Ng Specifying Perspective Projection From Angel and Shreiner, Interactive Computer Graphics CS184/284A Ren Ng Perspective Projection Parameterized by • fovy : vertical angular field of view • aspect : width / height of field of view • near : depth of near clipping plane • far : depth of far clipping plane Derived quantities • top = near * tan (fovy) • bottom = – top • right = top * aspect • left = – right CS184/284A Ren Ng Transforms Recap Transforms Recap Coordinate Systems • Object coordinates • Apply modeling transforms… • World (scene) coordinates • Apply viewing transform… • Camera (eye) coordinates • Apply perspective transform + homog.
Load more

Recommended publications
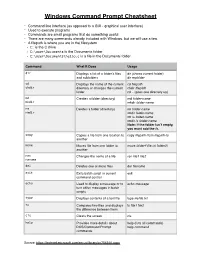
  • Windows Command Prompt Cheatsheet
    Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx.
    [Show full text]
  • Powerview Command Reference
    PowerView Command Reference TRACE32 Online Help TRACE32 Directory TRACE32 Index TRACE32 Documents ...................................................................................................................... PowerView User Interface ............................................................................................................ PowerView Command Reference .............................................................................................1 History ...................................................................................................................................... 12 ABORT ...................................................................................................................................... 13 ABORT Abort driver program 13 AREA ........................................................................................................................................ 14 AREA Message windows 14 AREA.CLEAR Clear area 15 AREA.CLOSE Close output file 15 AREA.Create Create or modify message area 16 AREA.Delete Delete message area 17 AREA.List Display a detailed list off all message areas 18 AREA.OPEN Open output file 20 AREA.PIPE Redirect area to stdout 21 AREA.RESet Reset areas 21 AREA.SAVE Save AREA window contents to file 21 AREA.Select Select area 22 AREA.STDERR Redirect area to stderr 23 AREA.STDOUT Redirect area to stdout 23 AREA.view Display message area in AREA window 24 AutoSTOre ..............................................................................................................................
    [Show full text]
  • Command Window – Basic Commands
    Command Window – Simple Commands help lists all commands p: switch to your P-drive c: switch to the computer’s C-drive dir list all files in a directory (aka “folder”); e.g. dir (list all files in current directory) dir myfolder (list all files in subdirectory myfolder) cd change directory; e.g. cd myfolder (move to subdirectory myfolder) cd .. (move up one directory level) md make (create) a directory; e.g. md myfolder (make a subdirectory called myfolder) copy copy files; e.g. copy oldfile newfile copy source.f90 myfolder\source.f90 ren rename files; e.g. ren oldfile newfile erase erase (delete) a file; e.g. (or del) erase unwanted.txt fc file compare; e.g. fc file1 file2 type list the contents of a file type somefile.txt type somefile.txt ¦ more (list contents, one page at a time) Wildcards (* and ?) Can be used to match length-unspecified strings (*) or individual letters (?); e.g. copy *.f90 *.bak dir solve.f?? Command Syntax and Options Most commands have various options; e.g. dir /p – list files, one page at a time To find the syntax and options available for any particular command use the /? option; e.g. dir /? History Use the and arrows on keyboard to recover previous commands. Use F7 to get a list of previous commands and arrow up and down to choose one to reissue. Editors An editor called notepad comes with the operating system: notepad myfile.f90 Running Programs You can run any program simply by typing its name; e.g. to run windows explorer: explorer Batch Files To avoid having to type a long sequence of commands it is convenient to put them all in a batch file – identified by the .bat extension.
    [Show full text]
  • MS-DOS Basics.Pdf
    MS-DOS Basics The Command Prompt When you first turn on your computer, you will see some cryptic information flash by. MS-DOS displays this information to let you know how it is configuring your computer. You can ignore it for now. When the information stops scrolling past, you'll see the following: C:\> This is called the command prompt or DOS prompt. The flashing underscore next to the command prompt is called the cursor. The cursor shows where the command you type will appear. Type the following command at the command prompt: ver The following message appears on your screen: MS-DOS version 6.22 Viewing the Contents of a Directory To view the contents of a directory 1. Type the following at the command prompt: dir A list similar to the following appears: Changing Directories To change from the root directory to the WINDOWS directory To change directories, you will use the cd command. The cd command stands for "change directory." 1. Type the following at the command prompt: cd windows The command prompt changes. It should now look like the following: C:\WINDOWS> Next, you will use the dir command to view a list of the files in the DOS directory. Viewing the Contents of WINDOWS Directory To view a list of the files in the WINDOWS directory 1. Type the following at the command prompt: dir Changing Back to the Root Directory To change to the root directory 1. Type the following at the command prompt: cd \ Note that the slash you type in this command is a backslash (\), not a forward slash (/).
    [Show full text]
  • Mkdir / MD Command :- This Command Is Used to Create the Directory in the Dos
    Department Of Computer Application (BBA) Dr. Rakesh Ranjan BCA Sem - 2 Operating system Mkdir / MD Command :- this command is used to create the directory in the dos . we can also create subdirectory within the directory by this command . we have to give path of the proposed directory to create. Syntax : c:\> mkdir abc This command create the directory abc on the c: drive C:\> md abc\cde It create subdirectory cde under abc directory C:\> md abc\pqr C:\md abc\cde\a C:\ md abc\cde\b C:\md abc\pqr\a C:\ md abc\pqr\b C:\md abc\pqr\a\c C:\ md abc\pqr\a\d The structure of the above created directory may be shown as ABC CDE PQR A B A B C D Tree command :- this command in dos is used to display the structure of the directory and subdirectory in DOS. C:\> tree This command display the structure of c: Drive C:\> tree abc It display the structure of abc directory on the c: drive Means that tree command display the directory structure of the given directory of given path. RD Command :- RD stands for Remove directory command . this command is used to remove the directory from the disk . it should be noted that directory which to be removed must be empty otherwise , can not be removed . Syntax :- c:\ rd abc It display error because , abc is not empty C:\ rd abc\cde It also display error because cde is not empty C:\ rd abc\cde\a It works and a directory will remove from the disk C:\ rd abc\cde\b It will remove the b directory C:\rd abc\cde It will remove the cde directory because cde is now empty.
    [Show full text]
  • Windows Command Line?
    Table of contents 1. Why an ebook on the Windows Command Line? 2. Make an example directory 3. A little exercise: open the Windows Command Prompt window and go to the example directory 3.1 The prompt 3.2 Moving into a (sub)directory 4. Pattern-matching 5. Command ‘DIR’ and Glob patterns 6. The ‘COPY’ command and Glob patterns 6.1 Copy files from the current directory into a subdirectory 6.2 Copy files from the current directory into a subdirectory in binary mode 6.3 Combine ASCII-files and put the result into a subdirectory 6.4 Combine binary files and put the result into a subdirectory 6.5 Are the files copied correctly? 6.6 Copy a selection of files with the ‘FOR’ loop 7. The ‘DEL’ command and Glob patterns 7.1 Delete files from the current directory 7.2 Delete files from the subdirectory ‘my Doc’ -1 7.3 Delete files from the subdirectory ‘my Doc’ -2 7.3.1 An alternative 7.3.2 ROBOCOPY 8. Passing multiple commands 9. The ‘REN’ or ‘RENAME’ command 9.1 Change subdirectory name 9.2 Change file extensions 9.3 Modify filenames from the current directory: basic examples 9.4 Truncate a filename by using ‘?’ 9.5 Modify filenames in the subdirectory ‘my Doc’: basic example 10. More complex replacements 10.1 Add a prefix to filenames with the same characters at the beginning 10.2 Add a prefix to filenames with the same extensions 10.3 Add a suffix at the end of filenames with the same extensions 10.4 Substitute a character in a specific position 11.
    [Show full text]
  • The Text (Command) Mode in Linux Environment
    Introduction to Linux Environment Yun-Wen Chen 1 The Text (Command) Mode in Linux Environment 2 The Main Operating Systems We May Meet 1. Windows 2. Mac 3. Linux (Unix) 3 Windows Command Mode and DOS Type “cmd” at here 4 Windows Command Mode and DOS DOS (before 1992) Common command: dir, cd, del, rd, erase, format, fdisk, print, ren, chkdsk Of course, you can run programs, games in it… 5 Like… 6 Mac Command Mode However, I am not a Mac user, I can not introduce you the great details of command mode in Mac. But I know Mac can open a command mode window (terminal) to login into a remove workstation. (usually in linux) 7 Linux Command Mode If you are a Linux user, you will be very familiar with the Linux commands in work station. Many computational scientists install Linux on their PC. However, the library and drivers are much harder to be found for executables than in windows and Mac. Example (Ubuntu) Click here 8 Linux Commands Linus DOS Commands Counterpart ls List directory contents dir cd Change directory cd mkdir Make a new directory md rmdir, rm -r Remove a directory Rd pwd Display directory location chdir rm Remove a file del cp Copy a file Copy mv Rename/move a file rename, move grep Look for a word in files given in command line Find cat Dump contents of a file to users screen type more Pipe output a single page at a time more More you can find on website: http://www.yolinux.com/TUTORIALS/unix_for_dos_users.html http://www.linuxdevcenter.com/cmd/ 9 How to Login into a Linux System (Workstation) 1.
    [Show full text]
  • MS-DOS Microsoft Disk Operating System
    emeronbEnßm MS-DOS Microsoft Disk Operating System 1-esckþIepþIm kñúgEpñkenH eyIgelIkykmkEtEpñkRKwHmYycMnUYn énRbB½n§tMeNIrkar edIm,IgayRsYl kñúgkar EsVgyl; MS-DOS nig eRbIR)as;bBa¢a rbs; . EtmunnwgsikSaeTAelIRbB½n§tMeNIrkar Gñk (Commad) DOS MS-DOS RtUvEsVgyl;eGay)anc,as;GMBIGVI ehAfa nig kñúg sin . File, Directory Directory Structure Windows - KWCasMnMuénÉksarEdlpÞúkenAelIépÞ rbs; ehIyvamaneQµaHtMNag nig File Media Disk TItaMgc,as;las;mYy . GacCakmµviFI Éksar b¤ File (Program), (Document) Collection of Data . .doc icon Extension Filename - KWCaTU b¤ CaftsMrab;pÞúkral; eTAtamRbePT gayRsYlcMnaM nig Directory or Folder Files EbgEck ehIyenAkñúg mYyGacmanftsMrab;pÞúkral; CaeRcInteTot ehAfa Directory Files Subdirectory or . Subfolder eTAkan; Path File POD.EXE 2-RbB½n§tMeNIrkarsMrab; IBM-PC kñúgEpñkenHeyIgnwgsikSa Cak;EsþgGMBI EdlCaRbePTkmµviFImYycMa)ac; CaTIbMput sMrab;RbePT DOS IBM-PC bc©úb,nñenH . mann½yfaenAmanRbB½n§tMeNIrkarepSg²CaeRcIneTot dUcCa sMrab;RbePT System Macintosh nigmanRbB½n§tMeNIrkar . UNIX,Windows ... RbB½n§tMeNIrkar KWCaRbB½n§kmµviFImYy eRbIsMrab;RtYtBinitüéntMeNIrkar RKb;RKgkarEbkEck (Operating System) nig eRbIR)as;épñkepSg² énma:sIundUcCa ryHeBlcaM)ac;sMrab; kareRbIR)as;én nwgk¾dUcCa CPU Memory bNþal]bkrN¾xageRkAepSg²eTot . 3- KWCaGVI DOS ? mkBIBaküfa mann½yfaCa RbB½n§tMeNIrkarrukrk nig eFVIkarelI DOS DISK OPERATING SYSTEM Disk (Harddisk or . vaCaRbB½n§RKb;RKg RKb;RKgÉksarenAelI dUcCakarcMlg lubnig karbegáIt Diskette) Disk Space Disk erobcMbegáIt b¤ .l. cUlGñkRsm½yemIlfaebIKµan RbB½n§tMeNIrkar Diectorys, Partition Track
    [Show full text]
  • Description of the Windows XP Recovery Console Page 1 of 7
    Page 1 of 7 Description of the Windows XP Recovery Console This article was previously published under Q314058 Article ID : 314058 For a Microsoft Windows 2000 version of this article, see 229716 (http://support.microsoft.com/kb/229716/). Last Review : May 7, 2007 Revision : 3.1 On This Page INTRODUCTION MORE INFORMATION Starting the Windows Recovery Console Using the Command Console Restrictions and limitations of the Recovery Console Available commands INTRODUCTION This article describes the functionality and limitations of the Windows Recovery Console. If your Microsoft Windows XP-based computer does not start correctly or if it does not start at all, you can use the Windows Recovery Console to help you recover your system software. This article discusses the following topics: • How to start the Windows Recovery Console. • How to use the Command Console. • Restrictions and limitations of the Windows Recovery Console. • The commands that are available in the Windows Recovery Console. MORE INFORMATION When you use the Windows Recovery Console, you can obtain limited access to the NTFS file system, FAT, and FAT32 volumes without starting the Windows graphical user interface (GUI). In the Windows Recovery Console, you can: • Use, copy, rename, or replace operating system files and folders. • Enable or disable service or device startup the next time that start your computer. • Repair the file system boot sector or the Master Boot Record (MBR). • Create and format partitions on drives. Note Only an administrator can obtain access to the Windows Recovery Console so that unauthorized users cannot use any NTFS volume. Starting the Windows Recovery Console To start the Windows Recovery Console, use one of the following methods: • Use the Windows Setup floppy disks or the Windows CD-ROM to start your computer.
    [Show full text]
  • Bad System Config Info Error in Windows 10/8/7 WHY BAD SYSTEM CONFIG INFO ERROR in WINDOWS 10/8/7
    Bad System Config Info Error In Windows 10/8/7 WHY BAD_SYSTEM_CONFIG_INFO ERROR IN WINDOWS 10/8/7 Here below are a few basic reasons that may cause bad system config info error in Windows 7/8/10 Corrupted or Damaged hard disk drive. Incorrectly configured corrupted device drivers. Corrupted Windows system files. Corrupted Windows registry files. Driver conflict between the new driver you installed. Corrupted/Damage RAM. METHOD 1: USING LAST KNOWN GOOD CONFIGURATION (ADVANCED) For Windows 10 or Windows 8: Step 1. First, you click Start and select Power > Press and hold Shift > Click on Restart. Step 2. Next, you select Troubleshoot > click Advanced Options > Click on Start Up settings. Step 3. Now you click on Restart. Step 4. After restarting Windows, the advanced boot options menu occurs in a black screen. You just choose Last known good configuration (Advanced) and tap Enter. For Windows 7 and older versions users: Step 1. First of all, you restart your computer. Step 2. When your computer powers up and shows a black scree white text or Windows logo, you hold or press F8 from your keyboard. Step 3. At this step, you’ll see the advanced boot menu in black screen. Choose the option Last known good configuration (Advanced) by arrow keys of your keyboard, then tap Enter. METHOD 2: USE WINDOWS MEMORY DIAGNOSTIC Step 1. You click Start Menu and type memory diagnostic, then select Windows Memory Diagnostic. Step 2. When Windows Memory Diagnostic window open, you click Restart now and check for problems (recommended). Step 3. Your computer will be restarted and check for RAM memory errors automatically.
    [Show full text]
  • Basic Ms-Dos
    8/23/2017 History ■ MS-DOS 1.0 was released in August 1981, and was updated until April 1994 when it BASIC MS-DOS was replaced by Windows 95 ■ All versions of windows still contain some type of DOS, in windows 95 and 98 you can go to run and type command to get to DOS prompt, in NT, 2000, and XP you can type ~ Dharma Raj Poudel CMD and get DOS. Introduction File Manipulation The role of DOS is to interpret commands that the user enters via the keyboard. DIR - Lists files and subdirectories • Wildcard Characters ? * EDIT - creates a new file or modifies an existing file These commands allow the following tasks to be COPY - copies a file or a group of files executed: XCOPY - copies all files in a directory (and its subdirectories) file and folder management DEL or ERASE - deletes a file or a group of files UNDELETE - undeletes files disk upgrades COPY (or XCOPY) plus DEL - moves files hardware configuration DOSKEY - recalls commands memory optimization RENAME or REN - renames files TYPE - displays text files program execution PRINT - prints a text file COPY - used to create a file ATTRIB - sets file properties FC - compares two files 1 8/23/2017 Directory Manipulation Basic Structure MD or MKDIR - creates a directory ■ Most DOS commands use the same CD or CHDIR - changes directory structure PROMPT - changes the command prompt ■ Command Source Destination /Switch TREE - displays the directory structure ■ The switch will give options to the command RD or RMDIR - removes a directory ■ Example COPY A:\file.txt c:\ /v ■ /v will verify if the file copied correctly REN - Renaming directories PATH - creates a search path The Help Switch /? MS-DOS Prompt ■ You can use the help switch with any command.
    [Show full text]
  • Datalight ROM-DOS User's Guide
    Datalight ROM-DOS User’s Guide Created: April 2005 Datalight ROM-DOS User’s Guide Copyright © 1999-2005 by Datalight, Inc . Portions copyright © GpvNO 2005 All Rights Reserved. Datalight, Inc. assumes no liability for the use or misuse of this software. Liability for any warranties implied or stated is limited to the original purchaser only and to the recording medium (disk) only, not the information encoded on it. U.S. Government Restricted Rights. Use, duplication, reproduction, or transfer of this commercial product and accompanying documentation is restricted in accordance with FAR 12.212 and DFARS 227.7202 and by a license agreement. THE SOFTWARE DESCRIBED HEREIN, TOGETHER WITH THIS DOCUMENT, ARE FURNISHED UNDER A SEPARATE SOFTWARE OEM LICENSE AGREEMENT AND MAY BE USED OR COPIED ONLY IN ACCORDANCE WITH THE TERMS AND CONDITIONS OF THAT AGREEMENT. Datalight and ROM-DOS are registered trademarks of Datalight, Inc. FlashFX ® is a trademark of Datalight, Inc. All other product names are trademarks of their respective holders. Part Number: 3010-0200-0716 Contents Chapter 1, ROM-DOS Introduction..............................................................................................1 About ROM-DOS ......................................................................................................................1 Conventions Used in this Manual .......................................................................................1 Terminology Used in this Manual ......................................................................................1
    [Show full text]