© Copyright 1999, Jim Loy (Some Alterations) People Sometimes Ask Me the Names of the Large Numbers

Total Page：16

File Type：pdf, Size：1020Kb

http://www.jimloy.com/math/billion.htm © Copyright 1999, Jim Loy (Some alterations) People sometimes ask me the names of the large numbers. Here is a table. The system used in the U.S. is not as logical as that used in other countries (like Great Britain, France, and Germany). In these other countries, a billion (bi meaning two) has twice as many zeros as a million, and a trillion (tri meaning three) has three times as many zeros as a million, etc. But the scientific community seems to use the American system. Exponential Number of zeros U.S. & scientific community Other countries Notation 3 x 103 thousand thousand 6 x 106 million million 9 x 109 billion 1000 million (1 milliard) 12 x 1012 trillion billion 15 x 1015 quadrillion 1000 billion 18 x 1018 quintillion trillion 21 x 1021 sextillion 1000 trillion 24 x 1024 septillion quadrillion 27 x 1027 octillion 1000 quadrillion 30 x 1030 nonillion quintillion 33 x 1033 decillion 1000 quintillion 36 x 1036 undecillion sextillion 39 x 1039 duodecillion 1000 sextillion 42 x 1042 tredecillion septillion 45 x 1045 quattuordecillion 1000 septillion 48 x 1048 quindecillion octillion 51 x 1051 sexdecillion 1000 octillion 54 x 1054 septendecillion nonillion 57 x 1057 octodecillion 1000 nonillion 60 x 1060 novemdecillion decillion 63 x 1063 vigintillion 1000 decillion 66 - 120 undecillion - vigintillion 303 x 10303 centillion 600 x 10600 centillion Addendum: There are other big numbers with names. A zillion has come to mean an arbitrary or unknown large number. A googol is 10^100. A googolplex is 10^googol (10^10^10^2). This number is too large to write here without exponents. Skewes' number (gesundheit) is 10^10^10^34 was used as an upper bound in a mathematical proof. Recently 10^10^10^10^10^7 was used in a proof. The googolplex has given rise to the n-plex notation: n-plex is 10^n. n-minex is 10^-n. Donald Knuth invented arrow notation, where m^n (^ is an up arrow) is the regular m^n. m^^n is m^m^m^m...^m, with n up arrows. m^^^n is m^^m^^m...^^m, with n ^^s. According to The Book of Numbers by J.H.Conway and R.K.Guy, chained arrow notation is the following enhancement: a^^^^^b is written as a>b>5, where > is a right arrow. .

Copy Link

Recommended publications

Large but Finite
Department of Mathematics MathClub@WMU Michigan Epsilon Chapter of Pi Mu Epsilon Large but Finite Drake Olejniczak Department of Mathematics, WMU What is the biggest number you can imagine? Did you think of a million? a billion? a septillion? Perhaps you remembered back to the time you heard the term googol or its show-off of an older brother googolplex. Or maybe you thought of infinity. No. Surely, `infinity' is cheating. Large, finite numbers, truly monstrous numbers, arise in several areas of mathematics as well as in astronomy and computer science. For instance, Euclid defined perfect numbers as positive integers that are equal to the sum of their proper divisors. He is also credited with the discovery of the first four perfect numbers: 6, 28, 496, 8128. It may be surprising to hear that the ninth perfect number already has 37 digits, or that the thirteenth perfect number vastly exceeds the number of particles in the observable universe. However, the sequence of perfect numbers pales in comparison to some other sequences in terms of growth rate. In this talk, we will explore examples of large numbers such as Graham's number, Rayo's number, and the limits of the universe. As well, we will encounter some fast-growing sequences and functions such as the TREE sequence, the busy beaver function, and the Ackermann function. Through this, we will uncover a structure on which to compare these concepts and, hopefully, gain a sense of what it means for a number to be truly large. 4 p.m. Friday October 12 6625 Everett Tower, WMU Main Campus All are welcome! http://www.wmich.edu/mathclub/ Questions? Contact Patrick Bennett ([email protected]) .
[Show full text]
Grade 7/8 Math Circles the Scale of Numbers Introduction
Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
[Show full text]
Maths Secrets of Simpsons Revealed in New Book
MONDAY 7 OCTOBER 2013 WWW.THEDAY.CO.UK Maths secrets of Simpsons revealed in new book The most successful TV show of all time is written by a team of brilliant ‘mathletes’, says writer Simon Singh, and full of obscure mathematical jokes. Can numbers really be all that funny? MATHEMATICS Nerd hero: The smartest girl in Springfield was created by a team of maths wizards. he world’s most popular cartoon a perfect number, a narcissistic number insist that their love of maths contrib- family has a secret: their lines are and a Mersenne Prime. utes directly to the more obvious humour written by a team of expert mathema- Another of these maths jokes – a black- that has made the show such a hit. Turn- Tticians – former ‘mathletes’ who are board showing 398712 + 436512 = 447212 ing intuitions about comedy into concrete as happy solving differential equa- – sent shivers down Simon Singh’s spine. jokes is like wrestling mathematical tions as crafting jokes. ‘I was so shocked,’ he writes, ‘I almost hunches into proofs and formulas. Comedy Now, science writer Simon Singh has snapped my slide rule.’ The numbers are and maths, says Cohen, are both explora- revealed The Simpsons’ secret math- a fake exception to a famous mathemati- tions into the unknown. ematical formula in a new book*. He cal rule known as Fermat’s Last Theorem. combed through hundreds of episodes One episode from 1990 features a Mathletes and trawled obscure internet forums to teacher making a maths joke to a class of Can maths really be funny? There are many discover that behind the show’s comic brilliant students in which Bart Simpson who will think comparing jokes to equa- exterior lies a hidden core of advanced has been accidentally included.
[Show full text]
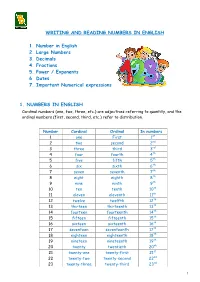
WRITING and READING NUMBERS in ENGLISH 1. Number in English 2
WRITING AND READING NUMBERS IN ENGLISH 1. Number in English 2. Large Numbers 3. Decimals 4. Fractions 5. Power / Exponents 6. Dates 7. Important Numerical expressions 1. NUMBERS IN ENGLISH Cardinal numbers (one, two, three, etc.) are adjectives referring to quantity, and the ordinal numbers (first, second, third, etc.) refer to distribution. Number Cardinal Ordinal In numbers 1 one First 1st 2 two second 2nd 3 three third 3rd 4 four fourth 4th 5 five fifth 5th 6 six sixth 6th 7 seven seventh 7th 8 eight eighth 8th 9 nine ninth 9th 10 ten tenth 10th 11 eleven eleventh 11th 12 twelve twelfth 12th 13 thirteen thirteenth 13th 14 fourteen fourteenth 14th 15 fifteen fifteenth 15th 16 sixteen sixteenth 16th 17 seventeen seventeenth 17th 18 eighteen eighteenth 18th 19 nineteen nineteenth 19th 20 twenty twentieth 20th 21 twenty-one twenty-first 21st 22 twenty-two twenty-second 22nd 23 twenty-three twenty-third 23rd 1 24 twenty-four twenty-fourth 24th 25 twenty-five twenty-fifth 25th 26 twenty-six twenty-sixth 26th 27 twenty-seven twenty-seventh 27th 28 twenty-eight twenty-eighth 28th 29 twenty-nine twenty-ninth 29th 30 thirty thirtieth 30th st 31 thirty-one thirty-first 31 40 forty fortieth 40th 50 fifty fiftieth 50th 60 sixty sixtieth 60th th 70 seventy seventieth 70 th 80 eighty eightieth 80 90 ninety ninetieth 90th 100 one hundred hundredth 100th 500 five hundred five hundredth 500th 1,000 One/ a thousandth 1000th thousand one thousand one thousand five 1500th 1,500 five hundred, hundredth or fifteen hundred 100,000 one hundred hundred thousandth 100,000th thousand 1,000,000 one million millionth 1,000,000 ◊◊ Click on the links below to practice your numbers: http://www.manythings.org/wbg/numbers-jw.html https://www.englisch-hilfen.de/en/exercises/numbers/index.php 2 We don't normally write numbers with words, but it's possible to do this.
[Show full text]
Simple Statements, Large Numbers
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Simple Statements, Large Numbers Shana Streeks University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Streeks, Shana, "Simple Statements, Large Numbers" (2007). MAT Exam Expository Papers. 41. https://digitalcommons.unl.edu/mathmidexppap/41 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Master of Arts in Teaching (MAT) Masters Exam Shana Streeks In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Gordon Woodward, Advisor July 2007 Simple Statements, Large Numbers Shana Streeks July 2007 Page 1 Streeks Simple Statements, Large Numbers Large numbers are numbers that are significantly larger than those ordinarily used in everyday life, as defined by Wikipedia (2007). Large numbers typically refer to large positive integers, or more generally, large positive real numbers, but may also be used in other contexts. Very large numbers often occur in fields such as mathematics, cosmology, and cryptography. Sometimes people refer to numbers as being “astronomically large”. However, it is easy to mathematically define numbers that are much larger than those even in astronomy. We are familiar with the large magnitudes, such as million or billion.
[Show full text]
1 Powers of Two
A. V. GERBESSIOTIS CS332-102 Spring 2020 Jan 24, 2020 Computer Science: Fundamentals Page 1 Handout 3 1 Powers of two Definition 1.1 (Powers of 2). The expression 2n means the multiplication of n twos. Therefore, 22 = 2 · 2 is a 4, 28 = 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 is 256, and 210 = 1024. Moreover, 21 = 2 and 20 = 1. Several times one might write 2 ∗ ∗n or 2ˆn for 2n (ˆ is the hat/caret symbol usually co-located with the numeric-6 keyboard key). Prefix Name Multiplier d deca 101 = 10 h hecto 102 = 100 3 Power Value k kilo 10 = 1000 6 0 M mega 10 2 1 9 1 G giga 10 2 2 12 4 T tera 10 2 16 P peta 1015 8 2 256 E exa 1018 210 1024 d deci 10−1 216 65536 c centi 10−2 Prefix Name Multiplier 220 1048576 m milli 10−3 Ki kibi or kilobinary 210 − 230 1073741824 m micro 10 6 Mi mebi or megabinary 220 40 n nano 10−9 Gi gibi or gigabinary 230 2 1099511627776 −12 40 250 1125899906842624 p pico 10 Ti tebi or terabinary 2 f femto 10−15 Pi pebi or petabinary 250 Figure 1: Powers of two Figure 2: SI system prefixes Figure 3: SI binary prefixes Definition 1.2 (Properties of powers). • (Multiplication.) 2m · 2n = 2m 2n = 2m+n. (Dot · optional.) • (Division.) 2m=2n = 2m−n. (The symbol = is the slash symbol) • (Exponentiation.) (2m)n = 2m·n. Example 1.1 (Approximations for 210 and 220 and 230).
[Show full text]
Big Numbers Tom Davis [email protected] September 21, 2011
Big Numbers Tom Davis [email protected] http://www.geometer.org/mathcircles September 21, 2011 1 Introduction The problem is that we tend to live among the set of puny integers and generally ignore the vast infinitude of larger ones. How trite and limiting our view! — P.D. Schumer It seems that most children at some age get interested in large numbers. “What comes after a thousand? After a million? After a billion?”, et cetera, are common questions. Obviously there is no limit; whatever number you name, a larger one can be obtained simply by adding one. But what is interesting is just how large a number can be expressed in a fairly compact way. Using the standard arithmetic operations (addition, subtraction, multiplication, division and exponentia- tion), what is the largest number you can make using three copies of the digit “9”? It’s pretty clear we should just stick to exponents, and given that, here are some possibilities: 999, 999, 9 999, and 99 . 9 9 Already we need to be a little careful with the final one: 99 . Does this mean: (99)9 or 9(9 )? Since (99)9 = 981 this interpretation would gain us very little. If this were the standard definition, then why c not write ab as abc? Because of this, a tower of exponents is always interpreted as being evaluated from d d c c c (c ) right to left. In other words, ab = a(b ), ab = a(b ), et cetera. 9 With this definition of towers of exponents, it is clear that 99 is the best we can do.
[Show full text]
Hyperoperations and Nopt Structures
Hyperoperations and Nopt Structures Alister Wilson Abstract (Beta version) The concept of formal power towers by analogy to formal power series is introduced. Bracketing patterns for combining hyperoperations are pictured. Nopt structures are introduced by reference to Nept structures. Briefly speaking, Nept structures are a notation that help picturing the seed(m)-Ackermann number sequence by reference to exponential function and multitudinous nestings thereof. A systematic structure is observed and described. Keywords: Large numbers, formal power towers, Nopt structures. 1 Contents i Acknowledgements 3 ii List of Figures and Tables 3 I Introduction 4 II Philosophical Considerations 5 III Bracketing patterns and hyperoperations 8 3.1 Some Examples 8 3.2 Top-down versus bottom-up 9 3.3 Bracketing patterns and binary operations 10 3.4 Bracketing patterns with exponentiation and tetration 12 3.5 Bracketing and 4 consecutive hyperoperations 15 3.6 A quick look at the start of the Grzegorczyk hierarchy 17 3.7 Reconsidering top-down and bottom-up 18 IV Nopt Structures 20 4.1 Introduction to Nept and Nopt structures 20 4.2 Defining Nopts from Nepts 21 4.3 Seed Values: “n” and “theta ) n” 24 4.4 A method for generating Nopt structures 25 4.5 Magnitude inequalities inside Nopt structures 32 V Applying Nopt Structures 33 5.1 The gi-sequence and g-subscript towers 33 5.2 Nopt structures and Conway chained arrows 35 VI Glossary 39 VII Further Reading and Weblinks 42 2 i Acknowledgements I’d like to express my gratitude to Wikipedia for supplying an enormous range of high quality mathematics articles.
[Show full text]
World Happiness REPORT Edited by John Helliwell, Richard Layard and Jeffrey Sachs World Happiness Report Edited by John Helliwell, Richard Layard and Jeffrey Sachs
World Happiness REPORT Edited by John Helliwell, Richard Layard and Jeffrey Sachs World Happiness reporT edited by John Helliwell, richard layard and Jeffrey sachs Table of ConTenTs 1. Introduction ParT I 2. The state of World Happiness 3. The Causes of Happiness and Misery 4. some Policy Implications references to Chapters 1-4 ParT II 5. Case study: bhutan 6. Case study: ons 7. Case study: oeCd 65409_Earth_Chapter1v2.indd 1 4/30/12 3:46 PM Part I. Chapter 1. InTrodUCTIon JEFFREY SACHS 2 Jeffrey D. Sachs: director, The earth Institute, Columbia University 65409_Earth_Chapter1v2.indd 2 4/30/12 3:46 PM World Happiness reporT We live in an age of stark contradictions. The world enjoys technologies of unimaginable sophistication; yet has at least one billion people without enough to eat each day. The world economy is propelled to soaring new heights of productivity through ongoing technological and organizational advance; yet is relentlessly destroying the natural environment in the process. Countries achieve great progress in economic development as conventionally measured; yet along the way succumb to new crises of obesity, smoking, diabetes, depression, and other ills of modern life. 1 These contradictions would not come as a shock to the greatest sages of humanity, including Aristotle and the Buddha. The sages taught humanity, time and again, that material gain alone will not fulfi ll our deepest needs. Material life must be harnessed to meet these human needs, most importantly to promote the end of suffering, social justice, and the attainment of happiness. The challenge is real for all parts of the world.
[Show full text]
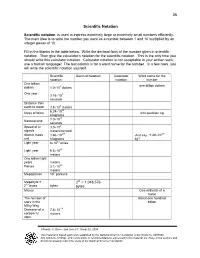
36 Scientific Notation
36 Scientific Notation Scientific notation is used to express extremely large or extremely small numbers efficiently. The main idea is to write the number you want as a number between 1 and 10 multiplied by an integer power of 10. Fill in the blanks in the table below. Write the decimal form of the number given in scientific notation. Then give the calculator’s notation for the scientific notation. This is the only time you should write this calculator notation. Calculator notation is not acceptable in your written work; use a human language! The last column is for a word name for the number. In a few rows, you will write the scientific notation yourself. Scientific Decimal Notation Calculator Word name for the notation notation number One billion one billion dollars dollars 1.0 ×10 9 dollars One year 3.16 ×10 7 seconds Distance from earth to moon 3.8 ×10 8 meters 6.24 ×10 23 Mass of Mars 624 sextillion kg kilograms 1.0 ×10 -9 Nanosecond seconds 8 Speed of tv 3.0 ×10 signals meters/second -27 -27 Atomic mass 1.66 ×10 Just say, “1.66 ×10 unit kilograms kg”! × 12 Light year 6 10 miles 15 Light year 9.5 ×10 meters One billion light years meters 16 Parsec 3.1 ×10 meters 6 Megaparsec 10 parsecs Megabyte = 220 = 1,048,576 20 2 bytes bytes bytes Micron One millionth of a meter The number of About one hundred stars in the billion Milky Way -14 Diameter of a 7.5 ×10 carbon-12 meters atom Rosalie A.
[Show full text]
Mathematical Constants and Sequences
Mathematical Constants and Sequences a selection compiled by Stanislav Sýkora, Extra Byte, Castano Primo, Italy. Stan's Library, ISSN 2421-1230, Vol.II. First release March 31, 2008. Permalink via DOI: 10.3247/SL2Math08.001 This page is dedicated to my late math teacher Jaroslav Bayer who, back in 1955-8, kindled my passion for Mathematics. Math BOOKS | SI Units | SI Dimensions PHYSICS Constants (on a separate page) Mathematics LINKS | Stan's Library | Stan's HUB This is a constant-at-a-glance list. You can also download a PDF version for off-line use. But keep coming back, the list is growing! When a value is followed by #t, it should be a proven transcendental number (but I only did my best to find out, which need not suffice). Bold dots after a value are a link to the ••• OEIS ••• database. This website does not use any cookies, nor does it collect any information about its visitors (not even anonymous statistics). However, we decline any legal liability for typos, editing errors, and for the content of linked-to external web pages. Basic math constants Binary sequences Constants of number-theory functions More constants useful in Sciences Derived from the basic ones Combinatorial numbers, including Riemann zeta ζ(s) Planck's radiation law ... from 0 and 1 Binomial coefficients Dirichlet eta η(s) Functions sinc(z) and hsinc(z) ... from i Lah numbers Dedekind eta η(τ) Functions sinc(n,x) ... from 1 and i Stirling numbers Constants related to functions in C Ideal gas statistics ... from π Enumerations on sets Exponential exp Peak functions (spectral) ..
[Show full text]
Download.Oracle.Com/Docs/Cd/B28359 01/Network.111/B28530/Asotr Ans.Htm
SCUOLA DI DOTTORATO IN INFORMATICA Tesi di Dottorato XXIV Ciclo A Distributed Approach to Privacy on the Cloud Francesco Pagano Relatore: Prof. Ernesto Damiani Correlatore: Prof. Stelvio Cimato Direttore della Scuola di Dottorato in Informatica: Prof. Ernesto Damiani Anno Accademico 2010/2011 Abstract The increasing adoption of Cloud-based data processing and storage poses a number of privacy issues. Users wish to preserve full control over their sensitive data and cannot accept it to be fully accessible to an external storage provider. Previous research in this area was mostly addressed at techniques to protect data stored on untrusted database servers; however, I argue that the Cloud architecture presents a number of specific problems and issues. This dissertation contains a detailed analysis of open issues. To handle them, I present a novel approach where confidential data is stored in a highly distributed partitioned database, partly located on the Cloud and partly on the clients. In my approach, data can be either private or shared; the latter is shared in a secure manner by means of simple grant-and-revoke permissions. I have developed a proof-of-concept implementation using an in-memory RDBMS with row-level data encryption in order to achieve fine-grained data access control. This type of approach is rarely adopted in conventional outsourced RDBMSs because it requires several complex steps. Benchmarks of my proof- of-concept implementation show that my approach overcomes most of the problems. 2 Acknowledgements I want to thank
[Show full text]