Hyperoperations and Nopt Structures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Introduction to Dependence Relations and Their Links to Algebraic Hyperstructures
mathematics Article Introduction to Dependence Relations and Their Links to Algebraic Hyperstructures Irina Cristea 1,* , Juš Kocijan 1,2 and Michal Novák 3 1 Centre for Information Technologies and Applied Mathematics, University of Nova Gorica, 5000 Nova Gorica, Slovenia; [email protected] 2 Department of Systems and Control, Jožef Stefan Institut, Jamova Cesta 39, 1000 Ljubljana, Slovenia 3 Faculty of Electrical Engineering and Communication, Brno University of Technology, Technická 10, 61600 Brno, Czech Republic; [email protected] * Correspondence: [email protected] or [email protected]; Tel.: +386-533-153-95 Received: 11 July 2019; Accepted: 19 September 2019; Published: 23 September 2019 Abstract: The aim of this paper is to study, from an algebraic point of view, the properties of interdependencies between sets of elements (i.e., pieces of secrets, atmospheric variables, etc.) that appear in various natural models, by using the algebraic hyperstructure theory. Starting from specific examples, we first define the relation of dependence and study its properties, and then, we construct various hyperoperations based on this relation. We prove that two of the associated hypergroupoids are Hv-groups, while the other two are, in some particular cases, only partial hypergroupoids. Besides, the extensivity and idempotence property are studied and related to the cyclicity. The second goal of our paper is to provide a new interpretation of the dependence relation by using elements of the theory of algebraic hyperstructures. Keywords: hyperoperation; hypergroupoid; dependence relation; influence; impact 1. Introduction In many real-life situations, there are contexts with numerous “variables”, which somehow depend on one another. -

Grade 7/8 Math Circles the Scale of Numbers Introduction
Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero. -

Maths Secrets of Simpsons Revealed in New Book
MONDAY 7 OCTOBER 2013 WWW.THEDAY.CO.UK Maths secrets of Simpsons revealed in new book The most successful TV show of all time is written by a team of brilliant ‘mathletes’, says writer Simon Singh, and full of obscure mathematical jokes. Can numbers really be all that funny? MATHEMATICS Nerd hero: The smartest girl in Springfield was created by a team of maths wizards. he world’s most popular cartoon a perfect number, a narcissistic number insist that their love of maths contrib- family has a secret: their lines are and a Mersenne Prime. utes directly to the more obvious humour written by a team of expert mathema- Another of these maths jokes – a black- that has made the show such a hit. Turn- Tticians – former ‘mathletes’ who are board showing 398712 + 436512 = 447212 ing intuitions about comedy into concrete as happy solving differential equa- – sent shivers down Simon Singh’s spine. jokes is like wrestling mathematical tions as crafting jokes. ‘I was so shocked,’ he writes, ‘I almost hunches into proofs and formulas. Comedy Now, science writer Simon Singh has snapped my slide rule.’ The numbers are and maths, says Cohen, are both explora- revealed The Simpsons’ secret math- a fake exception to a famous mathemati- tions into the unknown. ematical formula in a new book*. He cal rule known as Fermat’s Last Theorem. combed through hundreds of episodes One episode from 1990 features a Mathletes and trawled obscure internet forums to teacher making a maths joke to a class of Can maths really be funny? There are many discover that behind the show’s comic brilliant students in which Bart Simpson who will think comparing jokes to equa- exterior lies a hidden core of advanced has been accidentally included. -
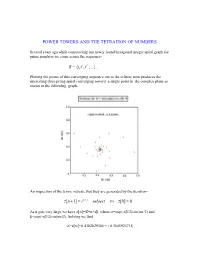
Power Towers and the Tetration of Numbers
POWER TOWERS AND THE TETRATION OF NUMBERS Several years ago while constructing our newly found hexagonal integer spiral graph for prime numbers we came across the sequence- i S {i,i i ,i i ,...}, Plotting the points of this converging sequence out to the infinite term produces the interesting three prong spiral converging toward a single point in the complex plane as shown in the following graph- An inspection of the terms indicate that they are generated by the iteration- z[n 1] i z[n] subject to z[0] 0 As n gets very large we have z[]=Z=+i, where =exp(-/2)cos(/2) and =exp(-/2)sin(/2). Solving we find – Z=z[]=0.4382829366 + i 0.3605924718 It is the purpose of the present article to generalize the above result to any complex number z=a+ib by looking at the general iterative form- z[n+1]=(a+ib)z[n] subject to z[0]=1 Here N=a+ib with a and b being real numbers which are not necessarily integers. Such an iteration represents essentially a tetration of the number N. That is, its value up through the nth iteration, produces the power tower- Z Z n Z Z Z with n-1 zs in the exponents Thus- 22 4 2 22 216 65536 Note that the evaluation of the powers is from the top down and so is not equivalent to the bottom up operation 44=256. Also it is clear that the sequence {1 2,2 2,3 2,4 2,...}diverges very rapidly unlike the earlier case {1i,2 i,3i,4i,...} which clearly converges. -

The Exponential Function
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 5-2006 The Exponential Function Shawn A. Mousel University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Mousel, Shawn A., "The Exponential Function" (2006). MAT Exam Expository Papers. 26. https://digitalcommons.unl.edu/mathmidexppap/26 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. The Exponential Function Expository Paper Shawn A. Mousel In partial fulfillment of the requirements for the Masters of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor May 2006 Mousel – MAT Expository Paper - 1 One of the basic principles studied in mathematics is the observation of relationships between two connected quantities. A function is this connecting relationship, typically expressed in a formula that describes how one element from the domain is related to exactly one element located in the range (Lial & Miller, 1975). An exponential function is a function with the basic form f (x) = ax , where a (a fixed base that is a real, positive number) is greater than zero and not equal to 1. The exponential function is not to be confused with the polynomial functions, such as x 2. One way to recognize the difference between the two functions is by the name of the function. -

Simple Statements, Large Numbers
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Simple Statements, Large Numbers Shana Streeks University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Streeks, Shana, "Simple Statements, Large Numbers" (2007). MAT Exam Expository Papers. 41. https://digitalcommons.unl.edu/mathmidexppap/41 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Master of Arts in Teaching (MAT) Masters Exam Shana Streeks In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Gordon Woodward, Advisor July 2007 Simple Statements, Large Numbers Shana Streeks July 2007 Page 1 Streeks Simple Statements, Large Numbers Large numbers are numbers that are significantly larger than those ordinarily used in everyday life, as defined by Wikipedia (2007). Large numbers typically refer to large positive integers, or more generally, large positive real numbers, but may also be used in other contexts. Very large numbers often occur in fields such as mathematics, cosmology, and cryptography. Sometimes people refer to numbers as being “astronomically large”. However, it is easy to mathematically define numbers that are much larger than those even in astronomy. We are familiar with the large magnitudes, such as million or billion. -

Categorical Comprehensions and Recursion Arxiv:1501.06889V2
Categorical Comprehensions and Recursion Joaquín Díaz Boilsa,∗ aFacultad de Ciencias Exactas y Naturales. Pontificia Universidad Católica del Ecuador. 170150. Quito. Ecuador. Abstract A new categorical setting is defined in order to characterize the subrecursive classes belonging to complexity hierarchies. This is achieved by means of coer- cion functors over a symmetric monoidal category endowed with certain recur- sion schemes that imitate the bounded recursion scheme. This gives a categorical counterpart of generalized safe composition and safe recursion. Keywords: Symmetric Monoidal Category, Safe Recursion, Ramified Recursion. 1. Introduction Various recursive function classes have been characterized in categorical terms. It has been achieved by considering a category with certain structure endowed with a recursion scheme. The class of Primitive Recursive Functions (PR in the sequel), for instance, has been chased simply by means of a carte- sian category and a Natural Numbers Object with parameters (nno in the sequel, see [11]). In [13] it can be found a generalization of that characterization to a monoidal setting, that is achieved by endowing a monoidal category with a spe- cial kind of nno (a left nno) where the tensor product is included. It is also known that other classes containing PR can be obtained by adding more struc- ture: considering for instance a topos ([8]), a cartesian closed category ([14]) or a category with finite limits ([12]).1 Less work has been made, however, on categorical characterizations of sub- arXiv:1501.06889v2 [math.CT] 28 Jan 2015 recursive function classes, that is, those contained in PR (see [4] and [5]). In PR there is at least a sequence of functions such that every function in it has a more complex growth than the preceding function in the sequence. -

Attributes of Infinity
International Journal of Applied Physics and Mathematics Attributes of Infinity Kiamran Radjabli* Utilicast, La Jolla, California, USA. * Corresponding author. Email: [email protected] Manuscript submitted May 15, 2016; accepted October 14, 2016. doi: 10.17706/ijapm.2017.7.1.42-48 Abstract: The concept of infinity is analyzed with an objective to establish different infinity levels. It is proposed to distinguish layers of infinity using the diverging functions and series, which transform finite numbers to infinite domain. Hyper-operations of iterated exponentiation establish major orders of infinity. It is proposed to characterize the infinity by three attributes: order, class, and analytic value. In the first order of infinity, the infinity class is assessed based on the “analytic convergence” of the Riemann zeta function. Arithmetic operations in infinity are introduced and the results of the operations are associated with the infinity attributes. Key words: Infinity, class, order, surreal numbers, divergence, zeta function, hyperpower function, tetration, pentation. 1. Introduction Traditionally, the abstract concept of infinity has been used to generically designate any extremely large result that cannot be measured or determined. However, modern mathematics attempts to introduce new concepts to address the properties of infinite numbers and operations with infinities. The system of hyperreal numbers [1], [2] is one of the approaches to define infinite and infinitesimal quantities. The hyperreals (a.k.a. nonstandard reals) *R, are an extension of the real numbers R that contains numbers greater than anything of the form 1 + 1 + … + 1, which is infinite number, and its reciprocal is infinitesimal. Also, the set theory expands the concept of infinity with introduction of various orders of infinity using ordinal numbers. -

Operations Per Se, to See If the Proposed Chi Is Indeed Fruitful
DOCUMENT RESUME ED 204 124 SE 035 176 AUTHOR Weaver, J. F. TTTLE "Addition," "Subtraction" and Mathematical Operations. 7NSTITOTION. Wisconsin Univ., Madison. Research and Development Center for Individualized Schooling. SPONS AGENCY Neional Inst. 1pf Education (ED), Washington. D.C. REPORT NO WIOCIS-PP-79-7 PUB DATE Nov 79 GRANT OS-NIE-G-91-0009 NOTE 98p.: Report from the Mathematics Work Group. Paper prepared for the'Seminar on the Initial Learning of Addition and' Subtraction. Skills (Racine, WI, November 26-29, 1979). Contains occasional light and broken type. Not available in hard copy due to copyright restrictions.. EDPS PRICE MF01 Plum Postage. PC Not Available from EDRS. DEseR.TPT00S *Addition: Behavioral Obiectives: Cognitive Oblectives: Cognitive Processes: *Elementary School Mathematics: Elementary Secondary Education: Learning Theories: Mathematical Concepts: Mathematics Curriculum: *Mathematics Education: *Mathematics Instruction: Number Concepts: *Subtraction: Teaching Methods IDENTIFIERS *Mathematics Education ResearCh: *Number 4 Operations ABSTRACT This-report opens by asking how operations in general, and addition and subtraction in particular, ante characterized for 'elementary school students, and examines the "standard" Instruction of these topics through secondary. schooling. Some common errors and/or "sloppiness" in the typical textbook presentations are noted, and suggestions are made that these probleks could lend to pupil difficulties in understanding mathematics. The ambiguity of interpretation .of number sentences of the VW's "a+b=c". and "a-b=c" leads into a comparison of the familiar use of binary operations with a unary-operator interpretation of such sentences. The second half of this document focuses on points of vier that promote .varying approaches to the development of mathematical skills and abilities within young children. -

Upper and Lower Bounds on Continuous-Time Computation
Upper and lower bounds on continuous-time computation Manuel Lameiras Campagnolo1 and Cristopher Moore2,3,4 1 D.M./I.S.A., Universidade T´ecnica de Lisboa, Tapada da Ajuda, 1349-017 Lisboa, Portugal [email protected] 2 Computer Science Department, University of New Mexico, Albuquerque NM 87131 [email protected] 3 Physics and Astronomy Department, University of New Mexico, Albuquerque NM 87131 4 Santa Fe Institute, 1399 Hyde Park Road, Santa Fe, New Mexico 87501 Abstract. We consider various extensions and modifications of Shannon’s General Purpose Analog Com- puter, which is a model of computation by differential equations in continuous time. We show that several classical computation classes have natural analog counterparts, including the primitive recursive functions, the elementary functions, the levels of the Grzegorczyk hierarchy, and the arithmetical and analytical hierarchies. Key words: Continuous-time computation, differential equations, recursion theory, dynamical systems, elementary func- tions, Grzegorczyk hierarchy, primitive recursive functions, computable functions, arithmetical and analytical hierarchies. 1 Introduction The theory of analog computation, where the internal states of a computer are continuous rather than discrete, has enjoyed a recent resurgence of interest. This stems partly from a wider program of exploring alternative approaches to computation, such as quantum and DNA computation; partly as an idealization of numerical algorithms where real numbers can be thought of as quantities in themselves, rather than as strings of digits; and partly from a desire to use the tools of computation theory to better classify the variety of continuous dynamical systems we see in the world (or at least in its classical idealization). -

The Notion Of" Unimaginable Numbers" in Computational Number Theory
Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers. -

An Introduction to Ramsey Theory Fast Functions, Infinity, and Metamathematics
STUDENT MATHEMATICAL LIBRARY Volume 87 An Introduction to Ramsey Theory Fast Functions, Infinity, and Metamathematics Matthew Katz Jan Reimann Mathematics Advanced Study Semesters 10.1090/stml/087 An Introduction to Ramsey Theory STUDENT MATHEMATICAL LIBRARY Volume 87 An Introduction to Ramsey Theory Fast Functions, Infinity, and Metamathematics Matthew Katz Jan Reimann Mathematics Advanced Study Semesters Editorial Board Satyan L. Devadoss John Stillwell (Chair) Rosa Orellana Serge Tabachnikov 2010 Mathematics Subject Classification. Primary 05D10, 03-01, 03E10, 03B10, 03B25, 03D20, 03H15. Jan Reimann was partially supported by NSF Grant DMS-1201263. For additional information and updates on this book, visit www.ams.org/bookpages/stml-87 Library of Congress Cataloging-in-Publication Data Names: Katz, Matthew, 1986– author. | Reimann, Jan, 1971– author. | Pennsylvania State University. Mathematics Advanced Study Semesters. Title: An introduction to Ramsey theory: Fast functions, infinity, and metamathemat- ics / Matthew Katz, Jan Reimann. Description: Providence, Rhode Island: American Mathematical Society, [2018] | Series: Student mathematical library; 87 | “Mathematics Advanced Study Semesters.” | Includes bibliographical references and index. Identifiers: LCCN 2018024651 | ISBN 9781470442903 (alk. paper) Subjects: LCSH: Ramsey theory. | Combinatorial analysis. | AMS: Combinatorics – Extremal combinatorics – Ramsey theory. msc | Mathematical logic and foundations – Instructional exposition (textbooks, tutorial papers, etc.). msc | Mathematical