Using the Fast Fourier Transform in HP 54600 Series Oscilloscopes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Look at SÉCAM III
Viewer License Agreement You Must Read This License Agreement Before Proceeding. This Scroll Wrap License is the Equivalent of a Shrink Wrap ⇒ Click License, A Non-Disclosure Agreement that Creates a “Cone of Silence”. By viewing this Document you Permanently Release All Rights that would allow you to restrict the Royalty Free Use by anyone implementing in Hardware, Software and/or other Methods in whole or in part what is Defined and Originates here in this Document. This Agreement particularly Enjoins the viewer from: Filing any Patents (À La Submarine?) on said Technology & Claims and/or the use of any Restrictive Instrument that prevents anyone from using said Technology & Claims Royalty Free and without any Restrictions. This also applies to registering any Trademarks including but not limited to those being marked with “™” that Originate within this Document. Trademarks and Intellectual Property that Originate here belong to the Author of this Document unless otherwise noted. Transferring said Technology and/or Claims defined here without this Agreement to another Entity for the purpose of but not limited to allowing that Entity to circumvent this Agreement is Forbidden and will NOT release the Entity or the Transfer-er from Liability. Failure to Comply with this Agreement is NOT an Option if access to this content is desired. This Document contains Technology & Claims that are a Trade Secret: Proprietary & Confidential and cannot be transferred to another Entity without that Entity agreeing to this “Non-Disclosure Cone of Silence” V.L.A. Wrapper. Combining Other Technology with said Technology and/or Claims by the Viewer is an acknowledgment that [s]he is automatically placing Other Technology under the Licenses listed below making this License Self-Enforcing under an agreement of Confidentiality protected by this Wrapper. -

Amiga Graphics Reference Card 2Nd Edition
Quick reference information for graphics, video, 2nd Edition desktop publishing, Covers new Amiga animation, and image 3000 graphics processing on the modes, 24-bit color Commodore Amiga hardware, DOS 2.0 personal computer. Reference Card overscan, and PAL. ) COLOR MODELS Additive Color Mixing Subtractive Color Mixing Red-Green-Blue Cube Hue-Saturation-Value Cone Cyan Value White Blue Blue] Axis Yellow Black ~reen Axis When mixi'hgpigments, cyan, yellow, Red When mixing light, red, green, and blue and magenta are primaries. Example: are primaries. Yell ow is formed by To get blue, mix cyan and magenta. Shades of gray are on the long Cyan pigment absorbs red, magenta adding red and green, for example. diagonal between black and white. pigment absorbs green, so the only component of white light that gets re The Visible Electromagnetic Spectrum flected is blue. 380 420 470 495 535 575 wavelength (nanometers) 770 Hue: Color; spectral position. Often measured in degrees; red=0°, yellow=60°, magenta=300°, etc. Hue is undefined for shades of gray. (ultraviolet) Purple Violet yellowish Red (infrared) Saturation: Color purity. A highly-saturated color is nearly Blue Orange monochromatic, i.e., contains only one color from the spectrum. White, black, and shades of gray have zero saturation. Value: The darkness of a color. How much black it contain's. DELUXE PAINT Ill KEYBOARD COMMANDS White has a value of one, black has a value of zero. Brush Painting Modes Page and Screen Commands While an animation is playing: ; ana, move brush along fixed axis -

IARU-R1 VHF Handbook
IARU-R1 VHF Handbook Vet Vers Version 9.01 March 2021 ion 8.12 IARU-R1 The content of this Handbook is the property of the International Amateur Radio Union, Region 1. Copying and publication of the content, or parts thereof, is allowed for non-commercial purposes provided the source of information is quoted. Contact information Website: http://www.iaru-r1.org/index.php/vhfuhsshf Newsletters: http://www.iaru- r1.org/index.php/documents/Documents/Newsletters/VHF-Newsletters/ Wiki http://iaruwiki.oevsv.at Contest robot http://iaru.oevsv.at/v_upld/prg_list.php VHF Handbook 9.00 1/180 IARU-R1 Oostende, 17 March 2021 Dear YL and OM, The Handbook consists of 5 PARTS who are covering all aspects of the VHF community: • PART 1: IARU-R1 VHF& up Organisation • PART 2: Bandplanning • PART 3: Contesting • PART 4: Technical and operational references • PART 5: archive This handbook is updated with the new VHF contest dates and rules and some typo’s in the rest of the handbook. Those changes are highlighted in yellow. The recommendations made during this Virtual General conference are highlighted in turquoise 73 de Jacques, ON4AVJ Secretary VHF+ committee (C5) IARU-R1 VHF Handbook 9.00 2/180 IARU-R1 CONTENT PART 1: IARU-1 VHF & UP ORGANISATION ORGANISATION 17 Constitution of the IARU Region 1 VHF/UHF/Microwaves Committee 17 In the Constitution: 17 In the Bye-laws: 17 Terms of reference of the IARU Region 1 VHF/UHF/Microwaves Committee 18 Tasks of IARU R-1 and its VHF/UHF/µWave Committee 19 Microwave managers Sub-committee 20 Coordinators of the VHF/UHF/Microwaves Committee 21 VHF Contest Coordinator 21 Satellite coordinator 21 Beacon coordinator 21 Propagations coordinators 21 Records coordinator 21 Repeater coordinator 21 IARU R-1 Executive Committee 21 Actual IARU-R1 VHF/UHF/SHF Chairman, Co-ordinators and co-workers 22 National VHF managers 23 Microwave managers 25 Note. -

Fourier Theory & Practice, Part II: Practice
Fourier Theory & Practice, Part II: Practice Operating the HP 54600 Series Scope with Measurement/Storage Module By: Robert Witte Hewlett-Packard Co. Practice Adding the Measurement/ Storage module to the scope adds additional waveform math capability, including FFT. These functions appear in the softkey menu under the ± (math) key. There are two math functions available, F1 and F2. The FFT function is available on Function F2. Function F2 can use function F1 as an operand, allowing an FFT to be performed on the result of F1. By setting function F1 to Channel 1 - Channel 2, and setting F2 to the FFT of F1, the FFT of a differential measurement can be obtained. The Measure- ment/Storage Module operating manual provides a more detailed discussion of these math functions. The scope can display the time domain waveform and the frequency domain spectrum simultaneously or individually. Normally, the sample points are not connected. For best frequency domain display, the sample points should be connected with lines (vectors). This can be accomplished by turning off all (time domain) channels and turning on only the FFT function. Alternatively, the Vectors On/Off softkey (on the Display menu) can be turned On and the STOP key pressed. Either of these actions allow the frequency domain samples to be connected by vectors which causes the display to appear more like a spectrum analyzer. The vertical axis of the FFT display is logarithmic, displayed in dBV (decibels relative to 1 Volt RMS). dB V = 20 log (VRMS) Thus, a 1 Volt RMS sinewave (2.8 Volts peak-to-peak) will read 0 dBV on the FFT display. -

NTSC Specifications
NTSC Modulation Standard ━━━━━━━━━━━━━━━━━━━━━━━━ The Impressionistic Era of TV. It©s Never The Same Color! The first analog Color TV system realized which is backward compatible with the existing B & W signal. To combine a Chroma signal with the existing Luma(Y)signal a quadrature sub-carrier Chroma signal is used. On the Cartesian grid the x & y axes are defined with B−Y & R−Y respectively. When transmitted along with the Luma(Y) G−Y signal can be recovered from the B−Y & R−Y signals. Matrixing ━━━━━━━━━ Let: R = Red \ G = Green Each range from 0 to 1. B = Blue / Y = Matrixed B & W Luma sub-channel. U = Matrixed Blue Chroma sub-channel. U #2900FC 249.76° −U #D3FC00 69.76° V = Matrixed Red Chroma sub-channel. V #FF0056 339.76° −V #00FFA9 159.76° W = Matrixed Green Chroma sub-channel. W #1BFA00 113.52° −W #DF00FA 293.52° HSV HSV Enhanced channels: Hue Hue I = Matrixed Skin Chroma sub-channel. I #FC6600 24.29° −I #0096FC 204.29° Q = Matrixed Purple Chroma sub-channel. Q #8900FE 272.36° −Q #75FE00 92.36° We have: Y = 0.299 × R + 0.587 × G + 0.114 × B B − Y = −0.299 × R − 0.587 × G + 0.886 × B R − Y = 0.701 × R − 0.587 × G − 0.114 × B G − Y = −0.299 × R + 0.413 × G − 0.114 × B = −0.194208 × (B − Y) −0.509370 × (R − Y) (−0.1942078377, −0.5093696834) Encode: If: U[x] = 0.492111 × ( B − Y ) × 0° ┐ Quadrature (0.4921110411) V[y] = 0.877283 × ( R − Y ) × 90° ┘ Sub-Carrier (0.8772832199) Then: W = 1.424415 × ( G − Y ) @ 235.796° Chroma Vector = √ U² + V² Chroma Hue θ = aTan2(V,U) [Radians] If θ < 0 then add 2π.[360°] Decode: SyncDet U: B − Y = -┼- @ 0.000° ÷ 0.492111 V: R − Y = -┼- @ 90.000° ÷ 0.877283 W: G − Y = -┼- @ 235.796° ÷ 1.424415 (1.4244145537, 235.79647610°) or G − Y = −0.394642 × (B − Y) − 0.580622 × (R − Y) (−0.3946423068, −0.5806217020) These scaling factors are for the quadrature Chroma signal before the 0.492111 & 0.877283 unscaling factors are applied to the B−Y & R−Y axes respectively. -
AD725 Data Sheet
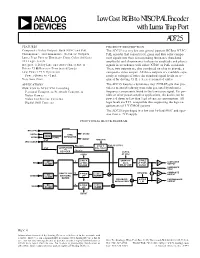
Low Cost RGB to NTSC/PAL Encoder a with Luma Trap Port AD725 FEATURES PRODUCT DESCRIPTION Composite Video Output: Both NTSC and PAL The AD725 is a very low cost general purpose RGB to NTSC/ Chrominance and Luminance (S-Video) Outputs PAL encoder that converts red, green and blue color compo- Luma Trap Port to Eliminate Cross Color Artifacts nent signals into their corresponding luminance (baseband TTL Logic Levels amplitude) and chrominance (subcarrier amplitude and phase) Integrated Delay Line and Auto-Tuned Filters signals in accordance with either NTSC or PAL standards. Drives 75 V Reverse-Terminated Loads These two outputs are also combined on-chip to provide a Low Power +5 V Operation composite video output. All three outputs are available sepa- Power-Down to <1 mA rately at voltages of twice the standard signal levels as re- Very Low Cost quired for driving 75 Ω, reverse-terminated cables. APPLICATIONS The AD725 features a luminance trap (YTRAP) pin that pro- RGB/VGA to NTSC/PAL Encoding vides a means of reducing cross color generated by subcarrier Personal Computers/Network Computers frequency components found in the luminance signal. For por- Video Games table or other power-sensitive applications, the device can be Video Conference Cameras powered down to less than 1 µA of current consumption. All Digital Still Cameras logic levels are TTL compatible thus supporting the logic re- quirements of 3 V CMOS systems. The AD725 is packaged in a low cost 16-lead SOIC and oper- ates from a +5 V supply. FUNCTIONAL BLOCK DIAGRAM NTSC/PAL HSYNC SYNC CSYNC XNOR VSYNC CSYNC SEPARATOR BURST 4FSC NTSC/PAL 4FSC CLOCK FSC 90؇C ؎180؇C FSC 90؇C/270؇C 4FSC QUADRATURE (PAL ONLY) +4 FSC 0؇C DECODER CLOCK CSYNC AT 8FSC 3-POLE SAMPLED- 2-POLE DC Y LUMINANCE RED LP PRE- DATA LP POST- X2 CLAMP OUTPUT FILTER DELAY LINE FILTER LUMINANCE TRAP U NTSC/PAL X2 COMPOSITE RGB-TO-YUV 4-POLE U ⌺ OUTPUT GREEN DC ENCODING LPF CLAMP CLAMP MATRIX BALANCED 4-POLE CHROMINANCE X2 MODULATORS LPF OUTPUT DC V 4-POLE V BLUE CLAMP LPF CLAMP BURST REV. -
Ics662-02 Ntsc/Pal Audio Clock
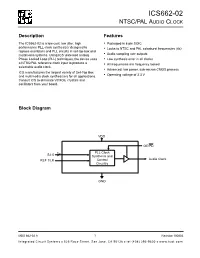
ICS662-02 NTSC/PAL AUDIO CLOCK Description Features The ICS662-02 is a low cost, low jitter, high • Packaged in 8 pin SOIC performance PLL clock synthesizer designed to • Locks to NTSC and PAL colorburst frequencies (4x) replace oscillators and PLL circuits in set-top box and multimedia systems. Using ICS’ patented analog • Audio sampling rate outputs Phase Locked Loop (PLL) techniques, the device uses • Low synthesis error in all clocks a NTSC/PAL reference clock input to produce a • All frequencies are frequency locked selectable audio clock. • Advanced, low power, sub-micron CMOS process ICS manufactures the largest variety of Set-Top Box and multimedia clock synthesizers for all applications. • Operating voltage of 3.3 V Consult ICS to eliminate VCXOs, crystals and oscillators from your board. Block Diagram VDD OE/PD 3 PLL Clock S2:0 Synthesis and REF CLK Control Audio Clock Circuitry GND MDS 662-02 A 1 Revision 100803 Integrated Circuit Systems 525 Race Street, San Jose, CA 95126 tel (408) 295-9800 www.icst.com ICS662-02 NTSC/PAL AUDIO CLOCK Pin Assignment CLOCK OUTPUT SELECT TABLE S2 S1 S0 Input Output Video REF 1 8 S0 Frequency Frequency Std. 000 14.31818 8.192 NTSC VDD 2 7 OE/PD 001 14.31818 11.2896 NTSC GND 3 6 S1 010 14.31818 12.288 NTSC S2 4 5 CLK 011 14.31818 24.576 NTSC 1 0 0 17.73447205* 8.192 PAL 8 pin (150 mil) SOIC 1 0 1 17.73447205* 11.2896 PAL 1 1 0 17.73447205* 12.288 PAL 1 1 1 17.73447205* 24.576 PAL * -0.16 ppm compared to PAL specification Pin Descriptions Pin Pin Pin Pin Description Number Name Type 1 REF Input Reference clock input. -

Retrocomputing on an FPGA Reconstructing an 80’S-Era Home Computer with Programmable Logic
by Stephen A. Edwards Retrocomputing on an FPGA Reconstructing an 80’s-Era Home Computer with Programmable Logic The author reconstructs a computer of his childhood, an Apple II+. As a Christmas present to myself in MOS Technology (it sold for $25 when 2007, I implemented an 1980s-era Apple an Intel 8080 sold for $179). The 6502 II+ in VHDL to run on an Altera DE2 had an eight-bit data bus and a 64K FPGA board. The point, aside from address space. In the Apple II+, the 6502 entertainment, was to illustrate the power ran at slightly above 1 MHz. Aside from (or rather, low power) of modern FPGAs. the ROMs and DRAMs, the rest of the Put another way, what made Steve Jobs circuitry consisted of discrete LS TTL his first million could be a class project chips (Photo 2). for the embedded systems class I teach at While the first Apple IIs shipped with Columbia University. 4K of DRAM, this quickly grew to a More seriously, this project standard of 48K. DRAMs, at this time, demonstrates how legacy digital were cutting-edge technology. While they electronics can be preserved and required periodic refresh and three power integrated with modern systems. While I supplies, their six-times higher density didn’t have an Apple II+ playing an made them worthwhile. important role in a system, many Along with with an integrated embedded systems last far longer than keyboard, a rudimentary (one-bit) sound their technology. The space shuttle port, and a game port that could sense immediately comes to mind; PDP-8s can buttons and potentiometers (e.g., in a be found running some signs for San joystick), the main feature of an Francisco’s BART system. -

NTSC Is the Analog Television System in Use in the United States and In
NTSC is the analog television system in use in the United States and in many other countries, including most of the Americas and some parts of East Asia It is named for the National Television System(s) Committee, the industry-wide standardization body that created it. History The National Television Systems Committee was established in 1940 by the Quick Facts about: Federal Communications Commission An independent governmeent agency that regulates interstate and international communications by radio and television and wire and cable and satelliteFederal Communications Commission to resolve the conflicts which had arisen between companies over the introduction of a nationwide analog television system in the U.S. The committee in March 1941 issued a technical standard for Quick Facts about: black and white A black-and-white photograph or slideblack and white television. In January 1950 the committee was reconstituted, this time to decide about color television, and in March 1953 it unanimously approved what is now called simply the NTSC color television standard. The updated standard retained full backwards compatibility with older black and white television sets. The standard has since been adopted by many other countries, for example most of Quick Facts about: the Americas North and South Americathe Americas and Quick Facts about: Japan A constitutional monarchy occupying the Japanese Archipelago; a world leader in electronics and automobile manufacture and ship buildingJapan. Technical details Refresh rate The NTSC format—or more correctly -

ISL59960 Datasheet
DATASHEET ISL59960 FN8358 960MegaQ™: An Automatic 960H and Composite Video Equalizer, Fully-Adaptive Rev 0.00 to 4000 Feet December 18, 2012 The ISL59960 is a single-channel adaptive equalizer for 960H Features (WD1) or 720H (D1) composite video designed to automatically compensate for long runs of CAT 5/CAT 6 or • Equalizes both 960H and 720H video RG-59 cable, producing high quality video output with no user • Equalizes up to 4000 feet of Cat 5/Cat 6 and up to 5000 interaction. The ISL59960 equalizes up to 4000 feet (1200 feet (1500m) of RG-59 meters) of CAT 5/CAT 6 cable. • Fully automatic, stand-alone operation - no user adjustment 960MegaQ™ compensates for high frequency cable losses of required up to 70dB at 9MHz, as well as source amplitude variations up • 13MHz -3dB bandwidth to ±3dB. • ±8kV ESD protection on all inputs The ISL59960 operates from a single +5V supply. Inputs are • Automatic cable type compensation AC-coupled and internally DC-restored. The output can drive 2VP-P into two source-terminated 75Ω loads (AC-coupled or • Compatible with color or monochrome, 960H, NTSC or PAL DC-coupled). signals • Automatic polarity detection and inversion Related Literature • Compensates for ±3dB source variation (in addition to cable • AN1780 “ISL59605-Catx-EVZ/ISL59960-Catx-EVZ losses) Evaluation Board” (Stand-Alone Evaluation Board) • Optional serial interface adds additional functionality • AN1776 “ISL59603-Coax-EVZ/ISL59960-Coax-EVZ • Works with single-ended or differential inputs Evaluation Board” (Stand-Alone Evaluation Board) -

TDS3VID Extended Video Application Module User Manual
User Manual TDS3VID Extended Video Application Module 071-0328-02 *P071032802* 071032802 Copyright E Tektronix. All rights reserved. Licensed software products are owned by Tektronix or its subsidiaries or suppliers, and are protected by national copyright laws and international treaty provisions. Tektronix products are covered by U.S. and foreign patents, issued and pending. Information in this publication supercedes that in all previously published material. Specifications and price change privileges reserved. TEKTRONIX, TEK, TEKPROBE, and TekSecure are registered trademarks of Tektronix, Inc. DPX, WaveAlert, and e*Scope are trademarks of Tektronix, Inc. Contacting Tektronix Tektronix, Inc. 14200 SW Karl Braun Drive P.O. Box 500 Beaverton, OR 97077 USA For product information, sales, service, and technical support: H In North America, call 1-800-833-9200. H Worldwide, visit www.tektronix.com to find contacts in your area. Contents Safety Summary............................. 2 Installing the Application Module................ 5 TDS3VID Features........................... 5 Accessing Extended Video Functions............ 7 Extended Video Conventions................... 10 Changes to the Video Trigger Menu.............. 11 Changes to the Display Menu................... 15 Changes to the Acquire Menu.................. 19 Video QuickMenu............................ 19 Examples.................................. 25 1 Safety Summary To avoid potential hazards, use this product only as specified. While using this product, you may need to access other parts of the system. Read the General Safety Summary in other system manuals for warnings and cautions related to operating the system. Preventing Electrostatic Damage CAUTION. Electrostatic discharge (ESD) can damage components in the oscilloscope and its accessories. To prevent ESD, observe these precautions when directed to do so. Use a Ground Strap. Wear a grounded antistatic wrist strap to discharge the static voltage from your body while installing or removing sensitive components. -

392 Part 74—Experimental Radio, Auxiliary, Special
Pt. 74 47 CFR Ch. I (10±1±98 Edition) RULES APPLY TO ALL SERVICES, AM, FM, AND RULES APPLY TO ALL SERVICES, AM, FM, AND TV, UNLESS INDICATED AS PERTAINING TO A TV, UNLESS INDICATED AS PERTAINING TO A SPECIFIC SERVICEÐContinued SPECIFIC SERVICEÐContinued [Policies of FCC are indicated (*)] [Policies of FCC are indicated (*)] Time of operation ................................. 73.1705 Use of multiplex subcarriersÐ Time, Limited ........................................ 73.1725 FM ................................................. 73.293 Time, Reference to .............................. 73.1209 TV .................................................. 73.665 Time, Share .......................................... 73.1715 Use of multiplex transmissions (AM) ... 73.127 Time Sharing, Operating schedule 73.561 (NCE±FM). V Time, Unlimited .................................... 73.1710 Vertical blanking interval, Tele- 73.646 Tolerances, Carrier frequency depar- 73.1545 communication service on. ture. Vertical plane radiation characteristics 73.160 Tolerances, Directional antenna sys- 73.62 Visual and aural TV transmitters, Op- 73.653 tem (AM). eration of. Tolerances, Operating power and 73.1560 Visual modulation monitoring equip- 73.691 mode. ment. Tone clusters: Audio attention-getting 73.4275 (*) W devices. Topographic data (FM) ........................ 73.3120 Want ads .............................................. 73.1212 Tower lighting and painting .................. 73.1213 Z Transferring a station ........................... 73.1150 Zone, Quiet