What Makes Time Different from Space?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Proofs with Perpendicular Lines
3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units. -
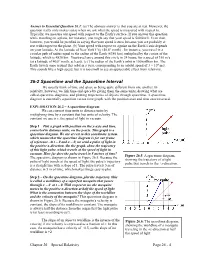
26-2 Spacetime and the Spacetime Interval We Usually Think of Time and Space As Being Quite Different from One Another
Answer to Essential Question 26.1: (a) The obvious answer is that you are at rest. However, the question really only makes sense when we ask what the speed is measured with respect to. Typically, we measure our speed with respect to the Earth’s surface. If you answer this question while traveling on a plane, for instance, you might say that your speed is 500 km/h. Even then, however, you would be justified in saying that your speed is zero, because you are probably at rest with respect to the plane. (b) Your speed with respect to a point on the Earth’s axis depends on your latitude. At the latitude of New York City (40.8° north) , for instance, you travel in a circular path of radius equal to the radius of the Earth (6380 km) multiplied by the cosine of the latitude, which is 4830 km. You travel once around this circle in 24 hours, for a speed of 350 m/s (at a latitude of 40.8° north, at least). (c) The radius of the Earth’s orbit is 150 million km. The Earth travels once around this orbit in a year, corresponding to an orbital speed of 3 ! 104 m/s. This sounds like a high speed, but it is too small to see an appreciable effect from relativity. 26-2 Spacetime and the Spacetime Interval We usually think of time and space as being quite different from one another. In relativity, however, we link time and space by giving them the same units, drawing what are called spacetime diagrams, and plotting trajectories of objects through spacetime. -

Classical Mechanics
Classical Mechanics Hyoungsoon Choi Spring, 2014 Contents 1 Introduction4 1.1 Kinematics and Kinetics . .5 1.2 Kinematics: Watching Wallace and Gromit ............6 1.3 Inertia and Inertial Frame . .8 2 Newton's Laws of Motion 10 2.1 The First Law: The Law of Inertia . 10 2.2 The Second Law: The Equation of Motion . 11 2.3 The Third Law: The Law of Action and Reaction . 12 3 Laws of Conservation 14 3.1 Conservation of Momentum . 14 3.2 Conservation of Angular Momentum . 15 3.3 Conservation of Energy . 17 3.3.1 Kinetic energy . 17 3.3.2 Potential energy . 18 3.3.3 Mechanical energy conservation . 19 4 Solving Equation of Motions 20 4.1 Force-Free Motion . 21 4.2 Constant Force Motion . 22 4.2.1 Constant force motion in one dimension . 22 4.2.2 Constant force motion in two dimensions . 23 4.3 Varying Force Motion . 25 4.3.1 Drag force . 25 4.3.2 Harmonic oscillator . 29 5 Lagrangian Mechanics 30 5.1 Configuration Space . 30 5.2 Lagrangian Equations of Motion . 32 5.3 Generalized Coordinates . 34 5.4 Lagrangian Mechanics . 36 5.5 D'Alembert's Principle . 37 5.6 Conjugate Variables . 39 1 CONTENTS 2 6 Hamiltonian Mechanics 40 6.1 Legendre Transformation: From Lagrangian to Hamiltonian . 40 6.2 Hamilton's Equations . 41 6.3 Configuration Space and Phase Space . 43 6.4 Hamiltonian and Energy . 45 7 Central Force Motion 47 7.1 Conservation Laws in Central Force Field . 47 7.2 The Path Equation . -

Time Reversal Symmetry in Cosmology and the Creation of a Universe–Antiuniverse Pair
universe Review Time Reversal Symmetry in Cosmology and the Creation of a Universe–Antiuniverse Pair Salvador J. Robles-Pérez 1,2 1 Estación Ecológica de Biocosmología, Pedro de Alvarado, 14, 06411 Medellín, Spain; [email protected] 2 Departamento de Matemáticas, IES Miguel Delibes, Miguel Hernández 2, 28991 Torrejón de la Calzada, Spain Received: 14 April 2019; Accepted: 12 June 2019; Published: 13 June 2019 Abstract: The classical evolution of the universe can be seen as a parametrised worldline of the minisuperspace, with the time variable t being the parameter that parametrises the worldline. The time reversal symmetry of the field equations implies that for any positive oriented solution there can be a symmetric negative oriented one that, in terms of the same time variable, respectively represent an expanding and a contracting universe. However, the choice of the time variable induced by the correct value of the Schrödinger equation in the two universes makes it so that their physical time variables can be reversely related. In that case, the two universes would both be expanding universes from the perspective of their internal inhabitants, who identify matter with the particles that move in their spacetimes and antimatter with the particles that move in the time reversely symmetric universe. If the assumptions considered are consistent with a realistic scenario of our universe, the creation of a universe–antiuniverse pair might explain two main and related problems in cosmology: the time asymmetry and the primordial matter–antimatter asymmetry of our universe. Keywords: quantum cosmology; origin of the universe; time reversal symmetry PACS: 98.80.Qc; 98.80.Bp; 11.30.-j 1. -

Pioneers in Optics: Christiaan Huygens
Downloaded from Microscopy Pioneers https://www.cambridge.org/core Pioneers in Optics: Christiaan Huygens Eric Clark From the website Molecular Expressions created by the late Michael Davidson and now maintained by Eric Clark, National Magnetic Field Laboratory, Florida State University, Tallahassee, FL 32306 . IP address: [email protected] 170.106.33.22 Christiaan Huygens reliability and accuracy. The first watch using this principle (1629–1695) was finished in 1675, whereupon it was promptly presented , on Christiaan Huygens was a to his sponsor, King Louis XIV. 29 Sep 2021 at 16:11:10 brilliant Dutch mathematician, In 1681, Huygens returned to Holland where he began physicist, and astronomer who lived to construct optical lenses with extremely large focal lengths, during the seventeenth century, a which were eventually presented to the Royal Society of period sometimes referred to as the London, where they remain today. Continuing along this line Scientific Revolution. Huygens, a of work, Huygens perfected his skills in lens grinding and highly gifted theoretical and experi- subsequently invented the achromatic eyepiece that bears his , subject to the Cambridge Core terms of use, available at mental scientist, is best known name and is still in widespread use today. for his work on the theories of Huygens left Holland in 1689, and ventured to London centrifugal force, the wave theory of where he became acquainted with Sir Isaac Newton and began light, and the pendulum clock. to study Newton’s theories on classical physics. Although it At an early age, Huygens began seems Huygens was duly impressed with Newton’s work, he work in advanced mathematics was still very skeptical about any theory that did not explain by attempting to disprove several theories established by gravitation by mechanical means. -

Chapter 5 ANGULAR MOMENTUM and ROTATIONS
Chapter 5 ANGULAR MOMENTUM AND ROTATIONS In classical mechanics the total angular momentum L~ of an isolated system about any …xed point is conserved. The existence of a conserved vector L~ associated with such a system is itself a consequence of the fact that the associated Hamiltonian (or Lagrangian) is invariant under rotations, i.e., if the coordinates and momenta of the entire system are rotated “rigidly” about some point, the energy of the system is unchanged and, more importantly, is the same function of the dynamical variables as it was before the rotation. Such a circumstance would not apply, e.g., to a system lying in an externally imposed gravitational …eld pointing in some speci…c direction. Thus, the invariance of an isolated system under rotations ultimately arises from the fact that, in the absence of external …elds of this sort, space is isotropic; it behaves the same way in all directions. Not surprisingly, therefore, in quantum mechanics the individual Cartesian com- ponents Li of the total angular momentum operator L~ of an isolated system are also constants of the motion. The di¤erent components of L~ are not, however, compatible quantum observables. Indeed, as we will see the operators representing the components of angular momentum along di¤erent directions do not generally commute with one an- other. Thus, the vector operator L~ is not, strictly speaking, an observable, since it does not have a complete basis of eigenstates (which would have to be simultaneous eigenstates of all of its non-commuting components). This lack of commutivity often seems, at …rst encounter, as somewhat of a nuisance but, in fact, it intimately re‡ects the underlying structure of the three dimensional space in which we are immersed, and has its source in the fact that rotations in three dimensions about di¤erent axes do not commute with one another. -

A Guide to Space Law Terms: Spi, Gwu, & Swf
A GUIDE TO SPACE LAW TERMS: SPI, GWU, & SWF A Guide to Space Law Terms Space Policy Institute (SPI), George Washington University and Secure World Foundation (SWF) Editor: Professor Henry R. Hertzfeld, Esq. Research: Liana X. Yung, Esq. Daniel V. Osborne, Esq. December 2012 Page i I. INTRODUCTION This document is a step to developing an accurate and usable guide to space law words, terms, and phrases. The project developed from misunderstandings and difficulties that graduate students in our classes encountered listening to lectures and reading technical articles on topics related to space law. The difficulties are compounded when students are not native English speakers. Because there is no standard definition for many of the terms and because some terms are used in many different ways, we have created seven categories of definitions. They are: I. A simple definition written in easy to understand English II. Definitions found in treaties, statutes, and formal regulations III. Definitions from legal dictionaries IV. Definitions from standard English dictionaries V. Definitions found in government publications (mostly technical glossaries and dictionaries) VI. Definitions found in journal articles, books, and other unofficial sources VII. Definitions that may have different interpretations in languages other than English The source of each definition that is used is provided so that the reader can understand the context in which it is used. The Simple Definitions are meant to capture the essence of how the term is used in space law. Where possible we have used a definition from one of our sources for this purpose. When we found no concise definition, we have drafted the definition based on the more complex definitions from other sources. -

Chapter 1 – Symmetry of Molecules – P. 1
Chapter 1 – Symmetry of Molecules – p. 1 - 1. Symmetry of Molecules 1.1 Symmetry Elements · Symmetry operation: Operation that transforms a molecule to an equivalent position and orientation, i.e. after the operation every point of the molecule is coincident with an equivalent point. · Symmetry element: Geometrical entity (line, plane or point) which respect to which one or more symmetry operations can be carried out. In molecules there are only four types of symmetry elements or operations: · Mirror planes: reflection with respect to plane; notation: s · Center of inversion: inversion of all atom positions with respect to inversion center, notation i · Proper axis: Rotation by 2p/n with respect to the axis, notation Cn · Improper axis: Rotation by 2p/n with respect to the axis, followed by reflection with respect to plane, perpendicular to axis, notation Sn Formally, this classification can be further simplified by expressing the inversion i as an improper rotation S2 and the reflection s as an improper rotation S1. Thus, the only symmetry elements in molecules are Cn and Sn. Important: Successive execution of two symmetry operation corresponds to another symmetry operation of the molecule. In order to make this statement a general rule, we require one more symmetry operation, the identity E. (1.1: Symmetry elements in CH4, successive execution of symmetry operations) 1.2. Systematic classification by symmetry groups According to their inherent symmetry elements, molecules can be classified systematically in so called symmetry groups. We use the so-called Schönfliess notation to name the groups, Chapter 1 – Symmetry of Molecules – p. 2 - which is the usual notation for molecules. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

Spacetime Symmetries and the Cpt Theorem
SPACETIME SYMMETRIES AND THE CPT THEOREM BY HILARY GREAVES A dissertation submitted to the Graduate School|New Brunswick Rutgers, The State University of New Jersey in partial fulfillment of the requirements for the degree of Doctor of Philosophy Graduate Program in Philosophy Written under the direction of Frank Arntzenius and approved by New Brunswick, New Jersey May, 2008 ABSTRACT OF THE DISSERTATION Spacetime symmetries and the CPT theorem by Hilary Greaves Dissertation Director: Frank Arntzenius This dissertation explores several issues related to the CPT theorem. Chapter 2 explores the meaning of spacetime symmetries in general and time reversal in particular. It is proposed that a third conception of time reversal, `geometric time reversal', is more appropriate for certain theoretical purposes than the existing `active' and `passive' conceptions. It is argued that, in the case of classical electromagnetism, a particular nonstandard time reversal operation is at least as defensible as the standard view. This unorthodox time reversal operation is of interest because it is the classical counterpart of a view according to which the so-called `CPT theorem' of quantum field theory is better called `PT theorem'; on this view, a puzzle about how an operation as apparently non- spatio-temporal as charge conjugation can be linked to spacetime symmetries in as intimate a way as a CPT theorem would seem to suggest dissolves. In chapter 3, we turn to the question of whether the CPT theorem is an essentially quantum-theoretic result. We state and prove a classical analogue of the CPT theorem for systems of tensor fields. This classical analogue, however, ii appears not to extend to systems of spinor fields. -

Geometry Course Outline
GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid -

A New Earth Study Guide.Pdf
A New Earth Study Guide Week 1 The consciousness that says ‘I am’ is not the consciousness that thinks. —Jean-Paul Sartre Affi rmation: "Through the guidance and wisdom of Spirit, I am being transformed by the renewing of my mind. All obstacles and emotions are stepping stones to the realization and appreciation of my sacred humanness." Study Questions – A New Earth (Review chapters 1 & 2, pp 1-58) Chapter 1: The Flowering of Human Consciousness Refl ect: Eckhart Tolle uses the image of the fi rst fl ower to begin his discussion of the transformation of consciousness. In your transformation, is this symbolism important to you? Describe. The two core insights of early religion are: 1) the normal state of human consciousness is dysfunctional (the Hindu call it maya – the veil of delusion) and 2) the opportunity for transformation is also in human consciousness (the Hindu call this enlightenment) (p. 8-9). What in your recent experience points to each of these insights? “To recognize one’s own insanity is, of course, the arising of sanity, the beginning of healing and transcendence” (p. 14). To what extent and in what circumstances (that you’re willing to discuss) does this statement apply to you? Religion is derived from the Latin word religare, meaning “to bind.” What, in your religious experience, have you been bound to? Stretching your imagination a bit, what could the word have pointed to in its original context? Spirit is derived from the Latin word spiritus, breath, and spirare, to blow. Aside from the allusion to hot air, how does this word pertain to your transformation? Do you consider yourself to be “spiritual” or “religious”? What examples of practices or beliefs can you give to illustrate? How does this passage from Revelation 21:1-4 relate to your transformation? Tease out as much of the symbolism as you can.