Emergency Trajectory Management for Transport Aircraft
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

200227 Liberation Of
THE LIBERATION OF OSS Leo van den Bergh, sitting on a pile of 155 mm grenades. Photo: City Archives Oss 1 September 2019, Oss 75 Years of Freedom The Liberation of Oss Oss, 01-09-2019 Copyright Arno van Orsouw 2019, Oss 75 Years of Freedom, the Liberation of Oss © 2019, Arno van Orsouw Research on city walks around 75 years of freedom in the centre of Oss. These walks have been developed by Arno van Orsouw at the request of City Archives Oss. Raadhuislaan 10, 5341 GM Oss T +31 (0) 0412 842010 Email: [email protected] Translation checked by: Norah Macey and Jos van den Bergh, Canada. ISBN: XX XXX XXXX X NUR: 689 All rights reserved. Subject to exceptions provided by law, nothing from this publication may be reproduced and / or made public without the prior written permission of the publisher who has been authorized by the author to the exclusion of everyone else. 2 Foreword Liberation. You can be freed from all kinds of things; usually it will be a relief. Being freed from war is of a different order of magnitude. In the case of the Second World War, it meant that the people of Oss had to live under the German occupation for more than four years. It also meant that there were men and women who worked for the liberation. Allied forces, members of the resistance and other groups; it was not without risk and they could lose their lives from it. During the liberation of Oss, on September 19, 1944, Sergeant L.W.M. -

Quarterly Aviation Report
Quarterly Aviation Report DUTCH SAFETY BOARD page 14 Investigations Within the Aviation sector, the Dutch Safety Board is required by law to investigate occurrences involving aircraft on or above Dutch territory. In addition, the Board has a statutory duty to investigate occurrences involving Dutch aircraft over open sea. Its October - December 2020 investigations are conducted in accordance with the Safety Board Kingdom Act and Regulation (EU) In this quarterly report, the Dutch Safety Board gives a brief review of the no. 996/2010 of the European past year. As a result of the COVID-19 pandemic, the number of commercial Parliament and of the Council of flights in the Netherlands was 52% lower than in 2019. The Dutch Safety 20 October 2010 on the Board therefore received fewer reports. In 2020, 27 investigations were investigation and prevention of started into serious incidents and accidents in the Netherlands. In addition, accidents and incidents in civil the Dutch Safety Board opened an investigation into a serious incident aviation. If a description of the involving a Boeing 747 in Zimbabwe in 2019. The Civil Aviation Authority page 7 events is sufficient to learn of Zimbabwe has delegated the entire conduct of the investigation to the lessons, the Board does not Netherlands, where the aircraft is registered and the airline is located. In the conduct any further investigation. past year, the Dutch Safety Board has offered and/or provided assistance to foreign investigative bodies thirteen times in investigations involving Dutch The Board’s activities are mainly involvement. aimed at preventing occurrences in the future or limiting their In this quarterly report you can read, among other things, about an consequences. -

Serving the Northern Netherlands Groningen Airport Eelde the Northern Netherlands: Groningen, Drenthe, Friesland
Serving the Northern Netherlands Groningen Airport Eelde The Northern Netherlands: Groningen, Drenthe, Friesland 10% of Dutch population The Guardian: Groningen happiest city of Europe From Cow to Google Groningen Airport Eelde (GRQ) is the only airport in the densely- populated Benelux/ Northwest Germany region that does not overlap catchment areas with other airports. GRQ is not slot-constrained and has capacity for growth. Copenhagen 2019 2014 London Best in class in Diary; Milk reservoir of Europe Worldclass Research Institutes; Agribusiness Van Hall Larenstein and University of Groningen International trade Nobel prize winning research (nanotech) Life Science, Modern and innovative business cluster Health & Medical Largest University Hospital in the Netherlands (12,141 employees) Organ Transplantation Hotspot Technology Abundance of feedstock Large scale green energy Energy Transition development Power to gas (Hydrogen) and Biobased Green dataport Eemshaven (data center development) Chemicals Green energy supply; 600 MW Gemini Wind International fiber connections Home to the smartest production facilities in the world World class materials research (Zernike Institute) High tech industry Big data Fleet management & Crewing Maritime sector Specialty ship building Tourism Culture Sports Within 30 minutes – 575,000 inhabitants Within 45 minutes – 1,279,000 inhabitants Within 60 minutes – 2,079,000 inhabitants Major leakage effect Minor leakage effect Route potential from GRQ Leakage analysis results Currently Destination Name Upper range -
Reference List Safety Approach Light Masts
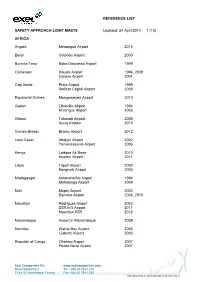
REFERENCE LIST SAFETY APPROACH LIGHT MASTS Updated: 24 April 2014 1 (10) AFRICA Angola Menongue Airport 2013 Benin Cotonou Airport 2000 Burkina Faso Bobo Diaulasso Airport 1999 Cameroon Douala Airport 1994, 2009 Garoua Airport 2001 Cap Verde Praia Airport 1999 Amilcar Capral Airport 2008 Equatorial Guinea Mongomeyen Airport 2010 Gabon Libreville Airport 1994 M’vengue Airport 2003 Ghana Takoradi Airport 2008 Accra Kotoka 2013 Guinea-Bissau Bissau Airport 2012 Ivory Coast Abidjan Airport 2002 Yamoussoukro Airport 2006 Kenya Laikipia Air Base 2010 Kisumu Airport 2011 Libya Tripoli Airport 2002 Benghazi Airport 2005 Madagasgar Antananarivo Airport 1994 Mahajanga Airport 2009 Mali Moptu Airport 2002 Bamako Airport 2004, 2010 Mauritius Rodrigues Airport 2002 SSR Int’l Airport 2011 Mauritius SSR 2012 Mozambique Airport in Mozambique 2008 Namibia Walvis Bay Airport 2005 Lüderitz Airport 2005 Republic of Congo Ollombo Airport 2007 Pointe Noire Airport 2007 Exel Composites Plc www.exelcomposites.com Muovilaaksontie 2 Tel. +358 20 754 1200 FI-82110 Heinävaara, Finland Fax +358 20 754 1330 This information is confidential unless otherwise stated REFERENCE LIST SAFETY APPROACH LIGHT MASTS Updated: 24 April 2014 2 (10) Brazzaville Airport 2008, 2010, 2013 Rwanda Kigali-Kamombe International Airport 2004 South Africa Kruger Mpumalanga Airport 2002 King Shaka Airport, Durban 2009 Lanseria Int’l Airport 2013 St. Helena Airport 2013 Sudan Merowe Airport 2007 Tansania Dar Es Salaam Airport 2009 Tunisia Tunis–Carthage International Airport 2011 ASIA China -

What Happens Next? Life in the Post-American World JANUARY 2014 VOL
Will mankind ARMED, DANGEROUS The reason New ‘solution’ to ever reach Europe has a lot more for world family problems: the stars? nukes than you think troubles Don’t have kids THE PHILADELPHIA TRUMPETJANUARY 2014 | thetrumpet.com What Happens Next? Life in the post-American world JANUARY 2014 VOL. 25, NO. 1 CIRC. 325,015 THE DANGER ZONE T A member of the German Air Force based in Alamogordo, New Mexico, prepares a Tornado aircraft for takeoff. How naive is America to entrust this immense firepower to nations that so recently—and throughout history— have proved to be enemies of the free world. WORLD COVER SOCIETY 1 FROM THE EDITOR Europe’s 20 How Did Family Get Nuclear Secret 2 What Happens After So Complicated? 18 INFOGRAPHIC American B61 a Superpower Dies? 34 SOCIETYWATCH Thermonuclear Weapons in The world is about to find out. Europe SCIENCE 23 Will Mankind Ever Reach 26 WORLDWATCH Unifying 7 Conquering the Holy Land the Stars? Europe’s military—through The cradle of civilization, the stage of the Crusades, the most contested the back door • North Africa’s territory on Earth—who will gain control now that America is gone? policeman • Is the president BIBLE purging the military of 31 PRINCIPLES OF LIVING 10 dissenters • Don’t underrate The World’s Next Superpower Mankind’s Aversion Therapy 12 Partnering with Latin America al Shabaab • No prize for you • Lesson 13 Africa’s powerful neighbor Moscow puts Soviet squeeze 35 COMMENTARY A Warning on neighbor nations of Hope 14 Czars and Emperors COVER If the U.S. -

Effect of the Traffic Distribution Rule on the Nature of Traffic Development at Lelystad Airport
EFFECT OF THE TRAFFIC DISTRIBUTION RULE ON THE NATURE OF TRAFFIC DEVELOPMENT AT LELYSTAD AIRPORT A study into market demand and dynamics following the opening of Lelystad Airport with a Traffic Distribution Rule (TDR) in place. CONTENTS EXECUTIVE SUMMARY 3 INTRODUCTION 7 2.1 Context 7 2.2 Objective of this study 7 2.3 Scope and limitations 8 APPROACH TO ESTIMATING TRAFFIC DEVELOPMENT 10 3.1 Logic used to determine traffic development 10 3.2 Methodology for determining traffic development at Lelystad Airport 11 3.3 Definition of autonomous versus non-autonomous traffic 11 FACTORS DRIVING TRAFFIC DEVELOPMENT 14 4.1 Demand outlook 14 4.2 Supply outlook 19 4.3 Airline market dynamics 26 TRAFFIC DEVELOPMENT SCENARIOS FOR LELYSTAD AIRPORT 38 5.1 Demand and supply balance in the Netherlands 38 5.2 Potential demand for slots at Lelystad Airport 39 5.3 Scenarios for slot allocation 41 OTHER FACTORS THAT COULD INFLUENCE TRAFFIC DEVELOPMENT 48 CONCLUSIONS 50 REFERENCES 52 1 EXECUTIVE SUMMARY 2 EXECUTIVE SUMMARY In this study, we have addressed the following question: “Can Lelystad Airport fulfil its targeted role of an overflow airport to Amsterdam Airport Schiphol (Schiphol) when the Traffic Distribution Rule (TDR) – supplemented by supportive measures if needed – is applied?” We conclude that Lelystad Airport will largely fulfil the role of an overflow airport, with an expected 10- 20% share of autonomous traffic in 2023 (at 10 thousand movements). This conclusion is based on the following two premises: 1. The share of autonomous traffic depends on how the EU Slot Regulation is specifically applied. -

2002 Statistical Annual Review (6.1 MB .Pdf)
Statistical Annual Review 2002 2002 Statistical Annual Review 2002 Preface April, 2003 In the case of the 2002 Annual Statistical Review, we felt that we had to respond to changes in the way that information can be presented. Whereas in the past this review largely consisted of tables supplemented with brief analyses, now the analyses have been greatly expanded and the number of tables have been kept to a minimum. Furthermore, we have now opted for a clear classification of the topics. The tables that are no longer included in the report are available on our website www.schiphol.nl. If you require any further information, please feel free to contact the department mentioned below. Data from this publication may be published as long as the source is quoted. Published by Amsterdam Airport Schiphol P.O. Box 7501 1118 ZG Schiphol Amsterdam Airport Schiphol Airlines Marketing & Account Management Statistics & Forecasts Phone : 31 (20) 601 2664 Fax : 31 (20) 601 4195 E-mail : [email protected] 3 Contents 1 Summary of developments 2002 5 Table: Traffic and transport summary 9 2 Aircraft movements 11 Table: Air transport movements, monthly totals 2002 17 Table: Air transport movements, annual totals 1993 - 2002 17 Map: Origins and destinations Europe 18 Map: Origins and destinations intercontinental 19 3 Passenger transport 21 Table: Passenger transport, monthly totals 2002 25 Table: Passenger transport, annual totals 1993 - 2002 25 4 Cargo transport 27 Table: Cargo transport, monthly totals 2002 32 Table: Cargo transport, annual totals 1993 - 2002 32 Table: Mail transport, annual totals 1993 - 2002 33 5 Other Airports 35 Table: Air transport movements 41 Table: Passenger transport (transit-direct counted once) 41 Table: Cargo transport 42 Table: Dutch airports 43 6 Infrastructure 45 4 Statistical Annual Review 2002 1. -

Geen Ontvangstbevestiging Afdelingen
Klarenbeek, 17 februari 2020 Kenmerk: lg16022020-01 Betreft: aanscherping handhavingsverzoek Ter attentie van: - Gedeputeerden C. van der Wal en P. Drenth, Provincie Gelderland - Team handhaving provincie Gelderland - Team handhaving gemeente Voorst - Team handhaving Inspectie Leefomgeving en Transport In kopie naar: - Statenleden provincie Gelderland - Verantwoordelijk gedeputeerden en wethouders - Gemeenteraad Apeldoorn, Voorst, Deventer en Zutphen - Pers Geachte ontvangers, Voorwoord: Schandalig, meer woorden hebben wij er niet voor!!! Na dat wij de afgelopen jaren al heel veel aandacht hebben gevraagd voor onze situatie, hebben wij op 5 februari 2020 een handhavingsverzoek met een duidelijk signaal afgegeven en wij hebben tot nu toe niet 1 reactie ontvangen (muv enkele geautomatiseerde berichten). Het is hiermee voor ons overduidelijk hoe de spreekwoordelijke vork in de steel zit. De belangen voor de aandeelhouders en vliegveld Teuge wegen dus zwaarder dan die van de inwoners. Daarnaast heeft de gemeente Apeldoorn deze week een motie behandeld inzake de stuitingsbrief Lelystad. Ook deze behandeling in de Raad heeft ons meer dan verbaasd (of eigenlijk niet). Het verschuilen achter een politieke lobby, het niet 100% achter je inwoners staan, de respectloze onderlinge opmerkingen en de Stentor maar verzoeken de inwoners te informeren samen met een raadsfractie, verder komen sommigen niet….wat een vertoning….Kijk u vooral de raadsvergadering terug via het raadsinformatie systeem van de gemeente Apeldoorn en zet u daarbij de bril van een inwoner op, redenerende uit burgerlogica (schrikt u ook zo…). Wel groots aangeven hoe goed je in verbinding staat met de actiegroepen, terwijl wij nog nooit 1 brief hebben ontvangen en nog nooit een antwoord hebben gehad op al onze brieven. -

Airline Split Operadons
Airline Split Opera-ons Dra final report October 16th, 2017 Confiden'al; for internal use only Execuve summary Key conclusions airline split operaons research Dra1 § The opening of Lelystad Airport may result in airlines operang from/to both Schiphol and Lelystad, serving the same catchment area, in a split operaon set up. This research describes what kind of airline split opera-on models exist and under which condions such operaon may or may not be sustainable. The basis for this research is an extensive analysis of flight schedules complemented with market developments. Client envisions a Traffic Distribu'on Rule (VVR) and requested to imply its implicaons. § The term ‘airline split operaons’ refers to network configuraons where an airline operates from its home base to mul'ple des'naons in the same catchment area or where an airline operates from another airport than its original home base in the same catchment area. The main types of split operaons are: ‘mul-airport’, ‘outside base’, ‘addional base’, and ‘second home base’. For the Dutch situaon the ‘second home base’ type is not relevant § All three relevant types of split opera-ons are being operated by airlines in the Dutch market for a long -me. From all regional airports in the Netherlands ‘outside base’ operaons are executed, while airlines have established ‘addional bases’ at Eindhoven and RoYerdam (partly due to the lack of development poten'al at Schiphol). Foreign airlines, mainly network carriers, but also low cost airlines, operate flights from their foreign home base to a second airport in the Netherlands next to Schiphol (‘mul+-airport’) or have done so in the past § The ‘Addi)onal base’ -type is well-suited for Lelystad from a market demand perspec've. -

Enschede Airport Twente
Arial photo (2000) Enschede Airport Twente 1:20.000 ENSCHEDE AIRPORT TWENTE 62 ENS - ENSCHEDE AIRPORT TWENTE AIRPORT-ORGANIZATION Enschede Airport Twente, Vliegveldweg 333, NL-7524 PT Enschede, Name / Address Netherlands Website www.enschede-airport.nl IATA / ICAO code ENS / EHTW Position (LAT/LONG) 52°16´37”N / 006°53´24”E Opening hours 06:45-22:30 hrs (Noise) restrictions night traffic Ownership Ministery of Defense Operator Enchede Airport Twente B.V. (civil) users Military air force (F16-base) + General Aviation License Article 33 Air traffic law, 24-09-1979 Shareholders Altenrhein realco AG - 40% Reggeborgh Invest BV-20% NV Beheer Luchthaven Twente-20% Oad Participaties BV-20% Comments: Ministery of Defense will close the airbase in 2007; Chambers of commerce is making a plan for continue civil airport (ACM,DHV,2004). FINANCE (x €1.000,-, 2002)* *(Source: Twente Airport Enschede, 2003) Annual report 2003 is not yet available. Company results: 826 Company costs: 825 -Airport charges 328 -Salaries & social costs 270 -Rentals & concessions 157 Investments: 12 REGION Regional profile Twente Nearest city: Enschede -Population (x 1.000): 153,0 -Potential market area 1hr by car 2hrs by car 1hr by train 2hrs by train weighted with distance decay (2004, x 1 million pax): 4,9 34,1 1,8 14,9 8,5 Business (airport linked): Business area Airport: 10 companies Employment (2003)*: *(Source: Enschede Airport Twente, 2004) -Employed direct 7 -Employed indirect 360 Airport Motorway Railway Nordhorn National border Built area Nijverdal Water Almelo Wierden Rijssen Borne Oldenzaal Enschede Rheine Hengelo Airport Losser Twente Enschede Gronau Haaksbergen Ahaus Twente region 1:300.000 ������� 64 ENS - AIR TRAFFIC CONNECTIVITY (summer 2004) Aircraft movements 1998-2003 150 Destinations: 6 0 0 0 . -

Quarterly Aviation Report
Quarterly Aviation Report DUTCH SAFETY BOARD page 5 Investigations Within the Aviation sector, the Dutch Safety Board is required by law to investigate occurrences involving aircraft on or above Dutch territory. In addition, the Board has a statutory duty to investigate occurrences involving Dutch aircraft over October - December 2018 open sea. Its investigations are conducted in accordance with the Safety Board Kingdom Act Those familiar with the aviation industry know that the Dutch Safety and Regulation (EU) no. 996/2010 Board investigates not only actual accidents, but that it also examines of the European Parliament and serious incidents that did not lead to an accident. The importance of such of the Council of 20 October investigation is self-evident, as it often leads to recommendations with an 2010 on the investigation and eye to further enhancing safety. It is for this reason that the Netherlands prevention of accidents and is indeed required, under the Chicago Convention, to investigate such incidents in civil aviation. If a incidents. page 9 description of the events is sufficient to learn lessons, the In this quarterly report, the Dutch Safety Board looks back at the serious Board does not conduct any incidents that occurred in 2018. Such investigations generally start with a further investigation. report from within the aviation industry, not necessarily because reporting incidents is mandatory, but because pilots and airlines are well aware of The Board’s activities are the vital importance of safety. In this respect, the aviation industry is clearly mainly aimed at preventing ahead of other industries in the Netherlands. -

Bijlage 3: Mailwsseiingen 2. Van: 1(2 2. -DGB Verzonden
Bijlage 3: mailwsseIingen 2. Van: 1(2 2. -DGB Verzonden: woensdag 20 april 2016 13:32 Aan: (Adecs Airinfra BV) airinfra.eu: (Adecs Airinfra BV): teuge-airportnl: @nlr.nl): conceptsnl): @teuge.eu): pcbovoorst.nl; @cbsdezaaier.nl); @brabant.nl @overijssel ni): @oviJ. ni @ovij. ni): @deventer. ni @deventer.nl): @voorst.nl tvoorst. ni Onderwerp: RE: Definitief verslag Expertmeeting geluidruimte luchthaven Teuge op 23 maart 2016 Beste te’. LC Mvg k Van: . e-. @gelderland.nl Verzonden: vrijdag 15 april 2016 16:17 Aan: (Adecs Airinfra BV) @airinfra.eu): (Adecs Airinfra BV): ©teuge-airport.nl): - DGB, @concepts.nl): capqemini.com @teuge.eu @pcbovoorst. nI @cbsdezaaier.nl @brabant.nl @overijssel.nl ovij.nl deventerni Onderwerp: Definitief verslag Expertmeeting geluidruimte luchthaven Teuge op 23 maart 2016 Beste mensen Bij mail van 25 maart om 14:21 uur zond ik u een conceptverslag van de Expertmeeting geluidruimte luchthaven Teuge die op 23 maart plaatsvond, vergezeld van de presentatie die adviesbureau Adecs Airinfra daar heeft verzorgd. Sindsdien mocht ik een aantal fekstuele reacties van u ontvangen, met behulp waaivan ik de verslaglegging verder heb kunnen aanscherpen en verduidelijken. Mijn excuses dat dit (als gevolg van grote drukte) toch nog een flinke tijd in beslag heeft genomen! Maar nu kan ik u dan alsnog de volgende stukken toesturen; a) de definitieve eindversie van hef expertmeeting-vers!ag (zie de eerste bijlage)-, b) de ter kennisname bijgevoegde ministeriële regeling van 9 december 1999 waarin de zogenoemde “min 3 Bkl-operatie” is geformaliseerd (zie de tweede bijlage) c) een aanvullende notitie van Adecs Airinfra die een aantal vragen beantwoordt die tijdens de expertmeeting niet of onvoldoende aan bod kwamen (zie de derde bijlage).