DOCSLIB.ORG

About This Booklet on Surface Areas and Volumes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
About This Booklet on Surface Areas and Volumes About This Booklet on Surface1 Areas and Volumes About This Booklet on Surface Areas and Volumes This Particular Booklet has been designed for the students of Math Class 10 (CBSE Board). However, it will also help those who have these chapters in their curriculum or want to gain the knowledge and explore the concepts. This Booklet explains: 1. Cube, Cuboid and Cylinder 2. Cone and Frustum 3. Sphere and Hemisphere 4. Combination of solids This Booklet also covers: 1. MCQs 2. Questions with Solutions 3. Questions for practice and 4. QR Codes to scan and watch videos on Surface Areas and Volumes QR codes when scanned with mobile scanner take you to our YouTube channel Let’sTute (www.youtube.com/letstute) where you can watch our free videos (need internet connection) on the topic. For Surface Areas and Volumes, in total, we have 8 videos which are accessible on several other platforms as described on the back cover of this Booklet. However, if there is any query, feel free to connect with us on the details given on the last page. Some other documents are also available: About Let’s Tute Let’sTute (Universal Learning Aid) is an E-learning company based in Mumbai, India. (www.letstute.com) We create content for Mathematics, Biology, Physics, Environmental Science, Book-Keeping & Accountancy and also a series on value education known as V2lead 2 13 .1 Cube, Cuboid and Cylinder Scan to watch the video on INTRODUCTION Surface area and Volume Surface Area: It is the sum of total exposed area of a three dimensional solid object. Its unit can be in the form cm2, m2 etc. Volume: It is the amount of space occupied by an object. Its unit can be cm3, m3, etc. Cuboid: A cuboid is the solid shape which has six rectangle faces at right angles to each other. Cube: A cube is a special form of cuboid which is bounded by six equal square faces. Right Circular Cylinder: A solid obtained by revolving a rectangular lamina about one of its sides, is called as Right Circular Cylinder. Total Surface Area and Volume for Cube, Cuboid and Cylinder MCQs (Multiple Choice Questions) 1. A cube is special type of cuboid. Scan to watch the video on A)True B)False Volume of cube, cuboid & cylinder 2. Volume of any object is nothing but its maximum capacity of storage. A)True B)False 3. A cube is three dimensional objects bounded by _ _ _ _ equal square faces. A)Five B)Six C)Four D) None of these 3 4. A cube of sides 6 m will have volume_ _ _ _ A)216 m2 B) 216 m3 C) 216 cm2 D) 216 m 5. If the radius of cylinder is doubled then the curved surface area of cylinder will be _ _ _ _ as compared to previous. A)Same B) Doubled C) Thrice D) None of these 6. What is the surface area of a cube having edges of length 15 cm? A)1350 B)225 C)1350 D) 1500 7. What iscm the length ofcm side of a cube ifcm the total surfacecm area of cube is 726 cm2? A)11 B)16 C)72 D) None of these 8. If thecm area of one face of cube cm is 169 cm2 thencm what will be the volume of cube. A) 1300 B) 4238 C) 5642 D) 2197 9. If the perimeter cm of onecm face of the cube is 28 cmcm then what willcm be its volume. A) 343 B) 343 C) 437 D) 473 10. What iscm the surface areacm of cuboid with cm dimension in m are cm 12×10×15 A) 1200 B) 900 C) 920 D) 940 11. Total Surfacem Area ofm Right Circularm Cylinder is _ _ _ _ m A) B) C) D) None of these 12. What 휋 ℎis the + curved surface 휋 areaℎ × of Cylinder 휋 ℎwhen − radius is 14 cm and height is 15 cm. [ π = 22/7] A) 1300 B) 2100 C) 1320 D) 4242 13. How many liters of water will be stored in a cylindrical tank of radius 3 m and height 7 m. [ Hint 1 m3 =1000 Liters take π = 22/7] A) 28640 B) 254000 C) 198000 D) None of these Answers: 퐿 퐿 퐿 1.(A), 2.(A), 3.(B), 4.(B), 5.(B), 6.(C), 7.(A), 8.(D), 9.(A) 10.(B) 11.(A) 12.(C) 13.(C) Solved Questions Q.1 Find the Total cost of painting the four walls of cuboidal room at the rate of 13 Rs per m2.The Dimension of the Cuboidal room are of length 10m , breadth 5m and height 6m. Given: For Cuboidal Room, Rate of Painting = 13 Rs/m2, l = 10m, b = 5m, h = 6m Solution: An Approach: As we have to paint only the walls, surface area of roof and floor so are not taken into calculation 4 Vertical surface area of cuboid (four walls) = = 2(10+5) × 6 + × 풉 h = 2(15) × 6 = 180 b Vertical surface area of cuboid = 180 m2. l Total cost of painting four walls = Vertical surface area of cuboid × Rate of painting wall/m2 = 180 m2 × 13 = 2340 Ans. Therefore Cost of Painting the four walls is Rs 2340 Q.2 A cuboidal pillar of dimension 600 cm × 55 cm × 25 cm made of wood which weights 200kg/m3. What will be the weight of the pillar? Given: Tips: Please remember to convert For Pillar [cuboid] dimensions from centimeter to meter as Length = 600cm = = 6m weight is given kg/m3. Breadth = 55cm = = 0.55m Height = 25cm = = 0.25m Solution: Volume of pillar [cuboid] = = 6 m × 0.55 m× 0.25 m = 0.825 × ×m 풉3 Weight of pillar = Volume of pillar × weight of volume per m3 = 0.825×200 = 165 Kg Ans. Weight of pillar =165 Kg Q.3 If the Diameter of a roller is 40 cm and length is 140 cm. It takes 350 revolutions to land a playground. Find the area of playground in m2. Given: The Diameter of cylindrical roller = 40 cm =0.4m An Approach: Please try to analyze Radius of cylindrical roller(r) = = 20 cm= 0.2 m that 1 revolution = lateral surface area Length of cylindrical roller (h) =140 cm = 1.4 m of cylinder. So 350 revolution = Solution: × 휋ℎ Curved surface area of cylindrical roller = = 흅풓풉 = × × . × . = 1.76 m2 Area covered in one revolution × ×is .= curved × . surface area of cylinder = 1.76 m2 5 Total Area of Playground = No. of revolutions × curved surface area of cylinder = 350 × 1.76 m2 = 616 m2 Ans. Area of Playground = 616 m2 Q.4 The curved surface area of cylinder is 154 cm2. The total surface area of the cylinder is thrice the curved surface area. Find the volume of cylinder. Given: Curved surface area of cylinder ( ) = 154 cm2 [훑 = ] Solution: Total surface area of cylinder = 3휋 ×ℎ curved surface area 154 + 2πr2 = 462 휋 ℎ + 2 휋πr2 = 462= – × 154 2πr2 = 308 2 × r×= = 2 × r = 49 × r = 7 Curved surface area of cylinder ( ) = 154 cm2 흅풓풉 × × × ℎ =h = h = 3.5 cm × Volume of Cylinder = = 흅풓 풉 = 539 cm3 × × × . Ans. Volume of Cylinder = 539 cm3 Practice Yourself Q1. Find the length of edges of cube having volume 512 cm3. Ans: 8 cm Q2. A Gift box of length 15 cm, breadth 13cm and height 14 cm need to be covered with a decorative wrapper. Find the area of wrapper needed. Ans: 1174 cm2 Q3. If a gas cylinder has an inner radius of 14 cm and height of 70 cm. How much maximum amount of gas can be stored in that cylinder? [π = 22/7] Ans: 43120 cm3 6 Q4.What will be the radius of cylinder if the curved surface area of cylinder is 1760 cm2 and its height is 14 cm? Ans: 20 cm Q5. If curved surface area of cylinder is 1188 cm2 and radius is 21 cm. What will be its volume? [Hint: first find the height using curved surface area] Ans: 12474 cm3 Q6. Find the curved surface area of cylinder when radius is 14 cm and height is 2 cm more than double of its radius. Ans: 2640 cm2 Make your own notes: 7 13 .2 Cone and Frustum INTRODUCTION Cone: A cone is a three-dimensional geometric shape that tapers smoothly from a flat circular base to a point called vertex. We can also define it as, “A solid obtained by revolving a right angled triangular lamina about any side (except hypotenuse) is a right circular cone.” Slant Height of a Cone (l) = Curved surface area of Cone = Total Surface Area of Cone = 풉 + 풓 흅풓풍 Volume of Cone = 흅풓풓 + 풍 흅풓 풉 l = slant height, r = radius of cone Frustum: If the cone is cut off by a plane parallel to the base not passing through vertex then we get the lower base portion as a frustum of cone. Where r1 and r2 are the radii of the ends of frustum (r1>r2) h = height and l = slant height Slant Height of the Frustum (l) = Curved surface area of Frustum = 풉 + 풓 − 풓 Total Surface Area of Frustum = 흅풓 + 풓풍 Volume of Frustum = 흅풓 + 풓풍 + 흅풓 + 흅풓 흅풓 + 풓 + 풓 × 풓풉 MCQs (Multiple Choice Questions) 1. If the radii of both the ends of frustum are same then it is a cylinder. A) True B) False 2. The volume of a cone is one third of the volume of the cylinder. A) True B) False 3. What is surface area of a cone with radius 7 cm and slant height 12 cm? A) 184 cm2 B) 418 cm2 C) 184 cm2 D) 284 cm2 4.
Load more

Recommended publications
  • A Technology to Synthesize 360-Degree Video Based on Regular Dodecahedron in Virtual Environment Systems*
    A Technology to Synthesize 360-Degree Video Based on Regular Dodecahedron in Virtual Environment Systems* Petr Timokhin 1[0000-0002-0718-1436], Mikhail Mikhaylyuk2[0000-0002-7793-080X], and Klim Panteley3[0000-0001-9281-2396] Federal State Institution «Scientific Research Institute for System Analysis of the Russian Academy of Sciences», Moscow, Russia 1 [email protected], 2 [email protected], 3 [email protected] Abstract. The paper proposes a new technology of creating panoramic video with a 360-degree view based on virtual environment projection on regular do- decahedron. The key idea consists in constructing of inner dodecahedron surface (observed by the viewer) composed of virtual environment snapshots obtained by twelve identical virtual cameras. A method to calculate such cameras’ projec- tion and orientation parameters based on “golden rectangles” geometry as well as a method to calculate snapshots position around the observer ensuring synthe- sis of continuous 360-panorama are developed. The technology and the methods were implemented in software complex and tested on the task of virtual observing the Earth from space. The research findings can be applied in virtual environment systems, video simulators, scientific visualization, virtual laboratories, etc. Keywords: Visualization, Virtual Environment, Regular Dodecahedron, Video 360, Panoramic Mapping, GPU. 1 Introduction In modern human activities the importance of the visualization of virtual prototypes of real objects and phenomena is increasingly grown. In particular, it’s especially required for training specialists in space and aviation industries, medicine, nuclear industry and other areas, where the mistake cost is extremely high [1-3]. The effectiveness of work- ing with virtual prototypes is significantly increased if an observer experiences a feeling of being present in virtual environment.
    [Show full text]
  • Cones, Pyramids and Spheres
    The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 YEARS 910 Cones, Pyramids and Spheres (Measurement and Geometry : Module 12) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 910 {4} A guide for teachers CONES, PYRAMIDS AND SPHERES ASSUMED KNOWLEDGE • Familiarity with calculating the areas of the standard plane figures including circles. • Familiarity with calculating the volume of a prism and a cylinder. • Familiarity with calculating the surface area of a prism. • Facility with visualizing and sketching simple three‑dimensional shapes. • Facility with using Pythagoras’ theorem. • Facility with rounding numbers to a given number of decimal places or significant figures.
    [Show full text]
  • Using History of Mathematics to Teach Volume Formula of Frustum Pyramids: Dissection Method
    Universal Journal of Educational Research 3(12): 1034-1048, 2015 http://www.hrpub.org DOI: 10.13189/ujer.2015.031213 Using History of Mathematics to Teach Volume Formula of Frustum Pyramids: Dissection Method Suphi Onder Butuner Department of Elementary Mathematics Education, Bozok University, Turkey Copyright © 2015 by authors, all rights reserved. Authors agree that this article remains permanently open access under the terms of the Creative Commons Attribution License 4.0 International License Abstract Within recent years, history of mathematics dynamic structure of mathematics [1, 2, 3, 4, 5, 6, 7]. It is (HoM) has become an increasingly popular topic. Studies stressed that history of mathematics will enrich the repertoire have shown that student reactions to it depend on the ways of teachers and develop their pedagogical content knowledge they use history of mathematics. The present action research [7, 8]. Jankvist [5] (2009) explains the use of history of study aimed to make students deduce volume rules of mathematics both as a tool and as a goal. History-as-a-tool frustum pyramids using the dissection method. Participants arguments are mainly concerned with learning of the inner were 24 grade eight students from Trabzon. Observations, issues of mathematics (mathematical concepts, theories, informal interviews and feedback forms were used as data methods, formulas), whereas history-as-a-goal arguments collection tools. Worksheets were distributed to students and are concerned with the use of history as a self-contained goal. the research was conducted in 3 class hours. Student views From the history-as-a-goal point of view, knowing about the on the activities were obtained through a written feedback history of mathematics is not a primary tool for learning form consisting of 4 questions.
    [Show full text]
  • Uniform Panoploid Tetracombs
    Uniform Panoploid Tetracombs George Olshevsky TETRACOMB is a four-dimensional tessellation. In any tessellation, the honeycells, which are the n-dimensional polytopes that tessellate the space, Amust by definition adjoin precisely along their facets, that is, their ( n!1)- dimensional elements, so that each facet belongs to exactly two honeycells. In the case of tetracombs, the honeycells are four-dimensional polytopes, or polychora, and their facets are polyhedra. For a tessellation to be uniform, the honeycells must all be uniform polytopes, and the vertices must be transitive on the symmetry group of the tessellation. Loosely speaking, therefore, the vertices must be “surrounded all alike” by the honeycells that meet there. If a tessellation is such that every point of its space not on a boundary between honeycells lies in the interior of exactly one honeycell, then it is panoploid. If one or more points of the space not on a boundary between honeycells lie inside more than one honeycell, the tessellation is polyploid. Tessellations may also be constructed that have “holes,” that is, regions that lie inside none of the honeycells; such tessellations are called holeycombs. It is possible for a polyploid tessellation to also be a holeycomb, but not for a panoploid tessellation, which must fill the entire space exactly once. Polyploid tessellations are also called starcombs or star-tessellations. Holeycombs usually arise when (n!1)-dimensional tessellations are themselves permitted to be honeycells; these take up the otherwise free facets that bound the “holes,” so that all the facets continue to belong to two honeycells. In this essay, as per its title, we are concerned with just the uniform panoploid tetracombs.
    [Show full text]
  • Volume of Prisms, Cones, Pyramids & Spheres
    Volume of Prisms, Cones, Pyramids & Spheres (H) A collection of 9-1 Maths GCSE Sample and Specimen questions from AQA, OCR, Pearson-Edexcel and WJEC Eduqas. Name: Total Marks: 1. A cylinder is made of bendable plastic. A dog’s toy is made by bending the cylinder to form a ring. The inner radius of the dog’s toy is 8 cm. The outer radius of the dog’s toy is 9 cm. Calculate an approximate value for the volume of the dog’s toy. State and justify what assumptions you have made in your calculations and the impact they have had on your results. [7] www.justmaths.co.uk Volume of Prisms, Cones, Pyramids & Spheres (H) - Version 2 January 2016 2. In this question all dimensions are in centimetres. A solid has uniform cross section. The cross section is a rectangle and a semicircle joined together. Work out an expression, in cm3, for the total volume of the solid. 1 Write your expression in the form ��3 + ��3 where � and � are integers. � [4] 3. A circular table top has radius 70 cm. (a) Calculate the area of the table top in cm2, giving your answer as a multiple of �. (a) ....................... cm2 [2] (b) The volume of the table top is 17 150� cm3. Calculate the thickness of the table top. (b) ........................ cm [2] www.justmaths.co.uk Volume of Prisms, Cones, Pyramids & Spheres (H) - Version 2 January 2016 4. The volume of Earth is 1.08 × 1012 km3. The volume of Jupiter is 1.43 × 1015 km3. How many times larger is the radius of Jupiter than the radius of Earth? Assume that Jupiter and Earth are both spheres.
    [Show full text]
  • A Mathematical Space Odyssey
    Contents Preface ix 1 Introduction 1 1.1Tenexamples......................... 1 1.2 Inhabitants of space . ..................... 9 1.3 Challenges .......................... 22 2 Enumeration 27 2.1Hexnumbers......................... 27 2.2Countingcalissons...................... 28 2.3 Using cubes to sum integers . ................ 29 2.4 Counting cannonballs ..................... 35 2.5 Partitioning space with planes ................ 37 2.6 Challenges .......................... 40 3 Representation 45 3.1 Numeric cubes as geometric cubes . ........... 45 3.2 The inclusion principle and the AM-GM inequality for threenumbers......................... 49 3.3Applicationstooptimizationproblems............ 52 3.4 Inequalities for rectangular boxes . ........... 55 3.5 Means for three numbers . ................ 59 3.6 Challenges .......................... 60 4 Dissection 65 4.1 Parallelepipeds, prisms, and pyramids . ........... 65 4.2 The regular tetrahedron and octahedron ........... 67 4.3 The regular dodecahedron . ................ 71 4.4Thefrustumofapyramid................... 72 4.5 The rhombic dodecahedron . ................ 74 4.6 The isosceles tetrahedron . ................ 76 4.7TheHadwigerproblem.................... 77 4.8 Challenges .......................... 79 xi xii Contents 5 Plane sections 83 5.1 The hexagonal section of a cube ............... 83 5.2Prismatoidsandtheprismoidalformula........... 85 5.3 Cavalieri’s principle and its consequences . ....... 89 5.4 The right tetrahedron and de Gua’s theorem . ....... 93 5.5 Inequalities
    [Show full text]
  • INTECH Infrared Interactive Whiteboard User Manual
    - 1 - INTECH IWB User Manual Xiamen Interactive Technology Co. Ltd INTECH Infrared Interactive Whiteboard User Manual - 2 - INTECH IWB User Manual Content Accessories List....................................................................................................................4 1. General Introduction.........................................................................................................6 1.1 What’s infrared interactive whiteboard?................................................................6 1.2 About this User Manual........................................................................................7 2. Preparation for using........................................................................................................7 2.1 How does the IWB work?.....................................................................................7 2.2 Requirements of the PC system...........................................................................7 2.2.1 The minimum system configuration...........................................................7 2.2.2 Requirement of the Operation System.......................................................7 2.2.3 System configuration recommended........................................................7 2.3 How to install the Infrared IWB？.........................................................................7 2.3.1 Installation for the mobile stand...............................................................8 2.3.2 Installation for the wall mounting................................................................9
    [Show full text]
  • Volume of a Pyramid Having a Square Base of Side 12Cm and Perpendicular Height of 14Cm
    Name: Exam Style Questions Ensure you have: Pencil, pen, ruler, protractor, pair of compasses and eraser You may use tracing paper if needed Guidance 1. Read each question carefully before you begin answering it. 2. Donʼt spend too long on one question. 3. Attempt every question. 4. Check your answers seem right. 5. Always show your workings Revision for this topic © CORBETTMATHS 2014 1.!A rectangular-based pyramid is shown below. !! !Calculate the volume of the pyramid. ........................cm" (2) 2.!A square-based pyramid has a base with side length 15cm. !The perpendicular height of the pyramid is 10cm. !Calculate the volume of the pyramid. ........................cm" (2) © CORBETTMATHS 2014 3.!A triangular-based pyramid is shown below. ! !Calculate the volume of the pyramid. ........................cm" (2) 4.!Calculate the volume of a pyramid having a square base of side 12cm and !perpendicular height of 14cm. ........................cm" (2) © CORBETTMATHS 2014 5.!Shown is a solid that is made of a pyramid and a cuboid. ! !Calculate the volume of the solid. ........................cm" (3) © CORBETTMATHS 2014 6.!Shown is a pyramid with volume 126cm" !! !Work out the vertical height. ........................cm (3) © CORBETTMATHS 2014 7. Shown is a square-based pyramid with volume 270cm" ! !Find the length of the side marked x. ........................cm (3) © CORBETTMATHS 2014 8.!DEFG is a triangle based pyramid. !The base DEF is an equilateral triangle with side 6cm. !The perpendicular height of the pyramid is 4cm. !! !Calculate the volume of the pyramid. ........................cm" (4) © CORBETTMATHS 2014 9.!A square based pyramid 1 is divided into two parts: !a square based pyramid 2 and a frustum 3, as shown.
    [Show full text]
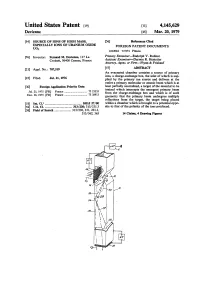
  • Source of Ions of High Mass, Especially Ions of Uranium Oxide UO 2
    United States Patent m [in 4,145,629 Devienne [45] Mar. 20,1979 [54] SOURCE OF IONS OF HIGH MASS, [56] References Cited ESPECIALLY IONS OF URANIUM OXIDE FOREIGN PATENT DOCUMENTS uo2 2212044 7/1974 France. [76] Inventor: Fernand M. Devienne, 117 La Primary Examiner—Rudolph V. Rolinec Croisett, 06400 Cannes, France Assistant Examiner— Darwin R. Hostetter Attorney, Agent, or Firm—Flynn & Frishauf [21] Appl. No.: 707,319 [57] ABSTRACT An evacuated chamber contains a source of primary ions, a charge-exchange box, the inlet of which is sup- [22] Filed: Jul. 21,1976 plied by the primary ion source and delivers at the outlet a primary molecular or atomic beam which is at [30] Foreign Application Priority Data least partially neutralized, a target of the material to be ionized which intercepts the emergent primary beam Jul. 25, 1975 [FR] France 75 23353 from the charge-exchange box and which is of such Dec. 18, 1975 [FR] France 75 38913 geometry that the primary beam undergoes multiple reflections from the target, the target being placed [51] Int. C1.2 H01J 27/00 within a chamber which is brought to a potential oppo- [52] U.S. Q 313/230; 313/231.3 site to that of the polarity of the ions produced. [58] Field of Search 313/230, 231, 231.3, 313/362, 363 14 Claims, 4 Drawing Figures U.S. Patent Mar. 20, 1979 Sheet 1 of 2 4,145,629 FIG. 1 U.S. Patent Mar. 20, 1979 Sheet 2 of 2 4,145,629 FIG. 3 FIG. 4 4,145,151 Should it be desired to remove the primary ions as SOURCE OF IONS OF HIGH MASS, ESPECIALLY these latter pass out of the charge-exchange box, provi- IONS OF URANIUM OXIDE U02 sion is advantageously made for primary ion deflecting plates consisting of electrodes brought to a potential This mvention relates to a source of ions of high mass, 5 such as to collect or deflect the primary ions to a suffi- especially ions of uranium oxide UO2.
    [Show full text]
  • 4.3 Volume of a Truncated Pyramid
    51 51 4 Easy cases 51 Fixing this broken symmetry will make a = b a natural easy case. One fully symmetric, dimensionless combination of a and b is log(a=b). This combination ranges between -1 and 1: -1 00 1 The special points in this range include the endpoints -1 and 1 cor- responding again to the easy cases a = 0 and b = 0 respectively; and the midpoint 0 corresponding to the third easy case a = b. In short, extreme cases are not the only easy cases; and easy cases also arise by equating symmetric quantities. Problem 4.7 Other symmetric combinations Invent other symmetric, dimensionless combinations of a and b – such as (a - b)=(a + b). Investigate whether those combinations have a = b as an interesting point. 4.3 Volume of a truncated pyramid The two preceding examples – the Gaussian integral (Section 4.1) and the area of an ellipse (Section 4.2) – used easy cases to check proposed formulas, as a method of analysis. The next level of sophistication – the next level in Bloom’s taxonomy [6] – is to use easy cases as a method of synthesis. As an example, start with a pyramid with a square a base and slice a piece from its top using a knife parallel to the base. This so-called frustum has h a square base and square top parallel to the base. Let its height be h, the side length of the base be b, and the side length of the top be a. What is b its volume? Since volume has dimensions of L3, candidates such as ab, ab3, and bh are impossible.
    [Show full text]
  • Solid Geometry with Problems and Applications (Revised Edition), by H
    The Project Gutenberg EBook of Solid Geometry with Problems and Applications (Revised edition), by H. E. Slaught and N. J. Lennes This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Solid Geometry with Problems and Applications (Revised edition) Author: H. E. Slaught N. J. Lennes Release Date: August 26, 2009 [EBook #29807] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK SOLID GEOMETRY *** Bonaventura Cavalieri (1598–1647) was one of the most influential mathematicians of his time. He was chiefly noted for his invention of the so-called “Principle of Indivisibles” by which he derived areas and volumes. See pages 143 and 214. SOLID GEOMETRY WITH PROBLEMS AND APPLICATIONS REVISED EDITION BY H. E. SLAUGHT, Ph.D., Sc.D. PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF CHICAGO AND N. J. LENNES, Ph.D. PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF MONTANA ALLYN and BACON Bo<on New York Chicago Produced by Peter Vachuska, Andrew D. Hwang, Chuck Greif and the Online Distributed Proofreading Team at http://www.pgdp.net transcriber’s note The original book is copyright, 1919, by H. E. Slaught and N. J. Lennes. Figures may have been moved with respect to the surrounding text. Minor typographical corrections and presentational changes have been made without comment. This PDF file is formatted for printing, but may be easily recompiled for screen viewing.
    [Show full text]
  • Civil Engineering Drawing
    SOLID OBJECT An object having three dimensions, i.e., length, breadth and height or thickness is called a SOLID. To represent a solid in the orthographic projection, at least two views are necessary; one view to represent length and height, called FRONT VIEW and the other view to represent length and breadth, called TOP VIEW. Sometimes the above two views may not be sufficient to explain the details. Hence a third view called View from the Right (Right Side View) or View from the Left (Left Side View) becomes necessary. HEIGHT BREADTH LENGTH Polyhedron The solid which is bounded by plane surfaces or faces is called polyhedron. The polyhedron are further sub-divided into three groups: . Regular Polyhedra . Prisms . Pyramids Regular Polyhedra A polyhedron is regular if each of its plane surfaces is a regular polygon. The regular plane surfaces which form the surfaces of the polyhedra are called Faces. The lines at which two faces intersect are called Edges. The three important regular polyhedra are: o Tetrahedron --------- 4 equal regular squares o Cube or Hexahedron -------- 6 equal regular squares o Octahedron ------------ 8 equal equilateral triangles Tetrahedron Cube or Hexahedron Octahedron 1 If the solids are not composed of similar surfaces, then such polyhedra may be classified into Prisms and Pyramids. Prism: A prism is a polyhedron having two equal and similar end faces called top face and bottom face (base) joined by other faces which may be Rectangles or Parallelograms. The imaginary line joining the centers of the faces is called the Axis. Top Face Longer edge Axis Rectangular Face Base Pyramids: A pyramid is a polyhedron having a plane figure for its base and equal number of isosceles triangular faces meeting at a point called Vertex or Apex.
    [Show full text]