A Mathematical Space Odyssey
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Technology to Synthesize 360-Degree Video Based on Regular Dodecahedron in Virtual Environment Systems*
A Technology to Synthesize 360-Degree Video Based on Regular Dodecahedron in Virtual Environment Systems* Petr Timokhin 1[0000-0002-0718-1436], Mikhail Mikhaylyuk2[0000-0002-7793-080X], and Klim Panteley3[0000-0001-9281-2396] Federal State Institution «Scientific Research Institute for System Analysis of the Russian Academy of Sciences», Moscow, Russia 1 [email protected], 2 [email protected], 3 [email protected] Abstract. The paper proposes a new technology of creating panoramic video with a 360-degree view based on virtual environment projection on regular do- decahedron. The key idea consists in constructing of inner dodecahedron surface (observed by the viewer) composed of virtual environment snapshots obtained by twelve identical virtual cameras. A method to calculate such cameras’ projec- tion and orientation parameters based on “golden rectangles” geometry as well as a method to calculate snapshots position around the observer ensuring synthe- sis of continuous 360-panorama are developed. The technology and the methods were implemented in software complex and tested on the task of virtual observing the Earth from space. The research findings can be applied in virtual environment systems, video simulators, scientific visualization, virtual laboratories, etc. Keywords: Visualization, Virtual Environment, Regular Dodecahedron, Video 360, Panoramic Mapping, GPU. 1 Introduction In modern human activities the importance of the visualization of virtual prototypes of real objects and phenomena is increasingly grown. In particular, it’s especially required for training specialists in space and aviation industries, medicine, nuclear industry and other areas, where the mistake cost is extremely high [1-3]. The effectiveness of work- ing with virtual prototypes is significantly increased if an observer experiences a feeling of being present in virtual environment. -

Cones, Pyramids and Spheres
The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 YEARS 910 Cones, Pyramids and Spheres (Measurement and Geometry : Module 12) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 910 {4} A guide for teachers CONES, PYRAMIDS AND SPHERES ASSUMED KNOWLEDGE • Familiarity with calculating the areas of the standard plane figures including circles. • Familiarity with calculating the volume of a prism and a cylinder. • Familiarity with calculating the surface area of a prism. • Facility with visualizing and sketching simple three‑dimensional shapes. • Facility with using Pythagoras’ theorem. • Facility with rounding numbers to a given number of decimal places or significant figures. -

Using History of Mathematics to Teach Volume Formula of Frustum Pyramids: Dissection Method
Universal Journal of Educational Research 3(12): 1034-1048, 2015 http://www.hrpub.org DOI: 10.13189/ujer.2015.031213 Using History of Mathematics to Teach Volume Formula of Frustum Pyramids: Dissection Method Suphi Onder Butuner Department of Elementary Mathematics Education, Bozok University, Turkey Copyright © 2015 by authors, all rights reserved. Authors agree that this article remains permanently open access under the terms of the Creative Commons Attribution License 4.0 International License Abstract Within recent years, history of mathematics dynamic structure of mathematics [1, 2, 3, 4, 5, 6, 7]. It is (HoM) has become an increasingly popular topic. Studies stressed that history of mathematics will enrich the repertoire have shown that student reactions to it depend on the ways of teachers and develop their pedagogical content knowledge they use history of mathematics. The present action research [7, 8]. Jankvist [5] (2009) explains the use of history of study aimed to make students deduce volume rules of mathematics both as a tool and as a goal. History-as-a-tool frustum pyramids using the dissection method. Participants arguments are mainly concerned with learning of the inner were 24 grade eight students from Trabzon. Observations, issues of mathematics (mathematical concepts, theories, informal interviews and feedback forms were used as data methods, formulas), whereas history-as-a-goal arguments collection tools. Worksheets were distributed to students and are concerned with the use of history as a self-contained goal. the research was conducted in 3 class hours. Student views From the history-as-a-goal point of view, knowing about the on the activities were obtained through a written feedback history of mathematics is not a primary tool for learning form consisting of 4 questions. -

Uniform Panoploid Tetracombs
Uniform Panoploid Tetracombs George Olshevsky TETRACOMB is a four-dimensional tessellation. In any tessellation, the honeycells, which are the n-dimensional polytopes that tessellate the space, Amust by definition adjoin precisely along their facets, that is, their ( n!1)- dimensional elements, so that each facet belongs to exactly two honeycells. In the case of tetracombs, the honeycells are four-dimensional polytopes, or polychora, and their facets are polyhedra. For a tessellation to be uniform, the honeycells must all be uniform polytopes, and the vertices must be transitive on the symmetry group of the tessellation. Loosely speaking, therefore, the vertices must be “surrounded all alike” by the honeycells that meet there. If a tessellation is such that every point of its space not on a boundary between honeycells lies in the interior of exactly one honeycell, then it is panoploid. If one or more points of the space not on a boundary between honeycells lie inside more than one honeycell, the tessellation is polyploid. Tessellations may also be constructed that have “holes,” that is, regions that lie inside none of the honeycells; such tessellations are called holeycombs. It is possible for a polyploid tessellation to also be a holeycomb, but not for a panoploid tessellation, which must fill the entire space exactly once. Polyploid tessellations are also called starcombs or star-tessellations. Holeycombs usually arise when (n!1)-dimensional tessellations are themselves permitted to be honeycells; these take up the otherwise free facets that bound the “holes,” so that all the facets continue to belong to two honeycells. In this essay, as per its title, we are concerned with just the uniform panoploid tetracombs. -

About This Booklet on Surface Areas and Volumes
About This Booklet on Surface1 Areas and Volumes About This Booklet on Surface Areas and Volumes This Particular Booklet has been designed for the students of Math Class 10 (CBSE Board). However, it will also help those who have these chapters in their curriculum or want to gain the knowledge and explore the concepts. This Booklet explains: 1. Cube, Cuboid and Cylinder 2. Cone and Frustum 3. Sphere and Hemisphere 4. Combination of solids This Booklet also covers: 1. MCQs 2. Questions with Solutions 3. Questions for practice and 4. QR Codes to scan and watch videos on Surface Areas and Volumes QR codes when scanned with mobile scanner take you to our YouTube channel Let’sTute (www.youtube.com/letstute) where you can watch our free videos (need internet connection) on the topic. For Surface Areas and Volumes, in total, we have 8 videos which are accessible on several other platforms as described on the back cover of this Booklet. However, if there is any query, feel free to connect with us on the details given on the last page. Some other documents are also available: About Let’s Tute Let’sTute (Universal Learning Aid) is an E-learning company based in Mumbai, India. (www.letstute.com) We create content for Mathematics, Biology, Physics, Environmental Science, Book-Keeping & Accountancy and also a series on value education known as V2lead 2 13 .1 Cube, Cuboid and Cylinder Scan to watch the video on INTRODUCTION Surface area and Volume Surface Area: It is the sum of total exposed area of a three dimensional solid object. -

Volume of Prisms, Cones, Pyramids & Spheres
Volume of Prisms, Cones, Pyramids & Spheres (H) A collection of 9-1 Maths GCSE Sample and Specimen questions from AQA, OCR, Pearson-Edexcel and WJEC Eduqas. Name: Total Marks: 1. A cylinder is made of bendable plastic. A dog’s toy is made by bending the cylinder to form a ring. The inner radius of the dog’s toy is 8 cm. The outer radius of the dog’s toy is 9 cm. Calculate an approximate value for the volume of the dog’s toy. State and justify what assumptions you have made in your calculations and the impact they have had on your results. [7] www.justmaths.co.uk Volume of Prisms, Cones, Pyramids & Spheres (H) - Version 2 January 2016 2. In this question all dimensions are in centimetres. A solid has uniform cross section. The cross section is a rectangle and a semicircle joined together. Work out an expression, in cm3, for the total volume of the solid. 1 Write your expression in the form ��3 + ��3 where � and � are integers. � [4] 3. A circular table top has radius 70 cm. (a) Calculate the area of the table top in cm2, giving your answer as a multiple of �. (a) ....................... cm2 [2] (b) The volume of the table top is 17 150� cm3. Calculate the thickness of the table top. (b) ........................ cm [2] www.justmaths.co.uk Volume of Prisms, Cones, Pyramids & Spheres (H) - Version 2 January 2016 4. The volume of Earth is 1.08 × 1012 km3. The volume of Jupiter is 1.43 × 1015 km3. How many times larger is the radius of Jupiter than the radius of Earth? Assume that Jupiter and Earth are both spheres. -

INTECH Infrared Interactive Whiteboard User Manual
- 1 - INTECH IWB User Manual Xiamen Interactive Technology Co. Ltd INTECH Infrared Interactive Whiteboard User Manual - 2 - INTECH IWB User Manual Content Accessories List....................................................................................................................4 1. General Introduction.........................................................................................................6 1.1 What’s infrared interactive whiteboard?................................................................6 1.2 About this User Manual........................................................................................7 2. Preparation for using........................................................................................................7 2.1 How does the IWB work?.....................................................................................7 2.2 Requirements of the PC system...........................................................................7 2.2.1 The minimum system configuration...........................................................7 2.2.2 Requirement of the Operation System.......................................................7 2.2.3 System configuration recommended........................................................7 2.3 How to install the Infrared IWB?.........................................................................7 2.3.1 Installation for the mobile stand...............................................................8 2.3.2 Installation for the wall mounting................................................................9 -

Volume of a Pyramid Having a Square Base of Side 12Cm and �Perpendicular Height of 14Cm
Name: Exam Style Questions Ensure you have: Pencil, pen, ruler, protractor, pair of compasses and eraser You may use tracing paper if needed Guidance 1. Read each question carefully before you begin answering it. 2. Donʼt spend too long on one question. 3. Attempt every question. 4. Check your answers seem right. 5. Always show your workings Revision for this topic © CORBETTMATHS 2014 1.!A rectangular-based pyramid is shown below. !! !Calculate the volume of the pyramid. ........................cm" (2) 2.!A square-based pyramid has a base with side length 15cm. !The perpendicular height of the pyramid is 10cm. !Calculate the volume of the pyramid. ........................cm" (2) © CORBETTMATHS 2014 3.!A triangular-based pyramid is shown below. ! !Calculate the volume of the pyramid. ........................cm" (2) 4.!Calculate the volume of a pyramid having a square base of side 12cm and !perpendicular height of 14cm. ........................cm" (2) © CORBETTMATHS 2014 5.!Shown is a solid that is made of a pyramid and a cuboid. ! !Calculate the volume of the solid. ........................cm" (3) © CORBETTMATHS 2014 6.!Shown is a pyramid with volume 126cm" !! !Work out the vertical height. ........................cm (3) © CORBETTMATHS 2014 7. Shown is a square-based pyramid with volume 270cm" ! !Find the length of the side marked x. ........................cm (3) © CORBETTMATHS 2014 8.!DEFG is a triangle based pyramid. !The base DEF is an equilateral triangle with side 6cm. !The perpendicular height of the pyramid is 4cm. !! !Calculate the volume of the pyramid. ........................cm" (4) © CORBETTMATHS 2014 9.!A square based pyramid 1 is divided into two parts: !a square based pyramid 2 and a frustum 3, as shown. -
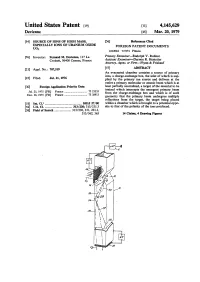
Source of Ions of High Mass, Especially Ions of Uranium Oxide UO 2
United States Patent m [in 4,145,629 Devienne [45] Mar. 20,1979 [54] SOURCE OF IONS OF HIGH MASS, [56] References Cited ESPECIALLY IONS OF URANIUM OXIDE FOREIGN PATENT DOCUMENTS uo2 2212044 7/1974 France. [76] Inventor: Fernand M. Devienne, 117 La Primary Examiner—Rudolph V. Rolinec Croisett, 06400 Cannes, France Assistant Examiner— Darwin R. Hostetter Attorney, Agent, or Firm—Flynn & Frishauf [21] Appl. No.: 707,319 [57] ABSTRACT An evacuated chamber contains a source of primary ions, a charge-exchange box, the inlet of which is sup- [22] Filed: Jul. 21,1976 plied by the primary ion source and delivers at the outlet a primary molecular or atomic beam which is at [30] Foreign Application Priority Data least partially neutralized, a target of the material to be ionized which intercepts the emergent primary beam Jul. 25, 1975 [FR] France 75 23353 from the charge-exchange box and which is of such Dec. 18, 1975 [FR] France 75 38913 geometry that the primary beam undergoes multiple reflections from the target, the target being placed [51] Int. C1.2 H01J 27/00 within a chamber which is brought to a potential oppo- [52] U.S. Q 313/230; 313/231.3 site to that of the polarity of the ions produced. [58] Field of Search 313/230, 231, 231.3, 313/362, 363 14 Claims, 4 Drawing Figures U.S. Patent Mar. 20, 1979 Sheet 1 of 2 4,145,629 FIG. 1 U.S. Patent Mar. 20, 1979 Sheet 2 of 2 4,145,629 FIG. 3 FIG. 4 4,145,151 Should it be desired to remove the primary ions as SOURCE OF IONS OF HIGH MASS, ESPECIALLY these latter pass out of the charge-exchange box, provi- IONS OF URANIUM OXIDE U02 sion is advantageously made for primary ion deflecting plates consisting of electrodes brought to a potential This mvention relates to a source of ions of high mass, 5 such as to collect or deflect the primary ions to a suffi- especially ions of uranium oxide UO2. -

4.3 Volume of a Truncated Pyramid
51 51 4 Easy cases 51 Fixing this broken symmetry will make a = b a natural easy case. One fully symmetric, dimensionless combination of a and b is log(a=b). This combination ranges between -1 and 1: -1 00 1 The special points in this range include the endpoints -1 and 1 cor- responding again to the easy cases a = 0 and b = 0 respectively; and the midpoint 0 corresponding to the third easy case a = b. In short, extreme cases are not the only easy cases; and easy cases also arise by equating symmetric quantities. Problem 4.7 Other symmetric combinations Invent other symmetric, dimensionless combinations of a and b – such as (a - b)=(a + b). Investigate whether those combinations have a = b as an interesting point. 4.3 Volume of a truncated pyramid The two preceding examples – the Gaussian integral (Section 4.1) and the area of an ellipse (Section 4.2) – used easy cases to check proposed formulas, as a method of analysis. The next level of sophistication – the next level in Bloom’s taxonomy [6] – is to use easy cases as a method of synthesis. As an example, start with a pyramid with a square a base and slice a piece from its top using a knife parallel to the base. This so-called frustum has h a square base and square top parallel to the base. Let its height be h, the side length of the base be b, and the side length of the top be a. What is b its volume? Since volume has dimensions of L3, candidates such as ab, ab3, and bh are impossible. -

Solid Geometry with Problems and Applications (Revised Edition), by H
The Project Gutenberg EBook of Solid Geometry with Problems and Applications (Revised edition), by H. E. Slaught and N. J. Lennes This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Solid Geometry with Problems and Applications (Revised edition) Author: H. E. Slaught N. J. Lennes Release Date: August 26, 2009 [EBook #29807] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK SOLID GEOMETRY *** Bonaventura Cavalieri (1598–1647) was one of the most influential mathematicians of his time. He was chiefly noted for his invention of the so-called “Principle of Indivisibles” by which he derived areas and volumes. See pages 143 and 214. SOLID GEOMETRY WITH PROBLEMS AND APPLICATIONS REVISED EDITION BY H. E. SLAUGHT, Ph.D., Sc.D. PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF CHICAGO AND N. J. LENNES, Ph.D. PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF MONTANA ALLYN and BACON Bo<on New York Chicago Produced by Peter Vachuska, Andrew D. Hwang, Chuck Greif and the Online Distributed Proofreading Team at http://www.pgdp.net transcriber’s note The original book is copyright, 1919, by H. E. Slaught and N. J. Lennes. Figures may have been moved with respect to the surrounding text. Minor typographical corrections and presentational changes have been made without comment. This PDF file is formatted for printing, but may be easily recompiled for screen viewing. -

Civil Engineering Drawing
SOLID OBJECT An object having three dimensions, i.e., length, breadth and height or thickness is called a SOLID. To represent a solid in the orthographic projection, at least two views are necessary; one view to represent length and height, called FRONT VIEW and the other view to represent length and breadth, called TOP VIEW. Sometimes the above two views may not be sufficient to explain the details. Hence a third view called View from the Right (Right Side View) or View from the Left (Left Side View) becomes necessary. HEIGHT BREADTH LENGTH Polyhedron The solid which is bounded by plane surfaces or faces is called polyhedron. The polyhedron are further sub-divided into three groups: . Regular Polyhedra . Prisms . Pyramids Regular Polyhedra A polyhedron is regular if each of its plane surfaces is a regular polygon. The regular plane surfaces which form the surfaces of the polyhedra are called Faces. The lines at which two faces intersect are called Edges. The three important regular polyhedra are: o Tetrahedron --------- 4 equal regular squares o Cube or Hexahedron -------- 6 equal regular squares o Octahedron ------------ 8 equal equilateral triangles Tetrahedron Cube or Hexahedron Octahedron 1 If the solids are not composed of similar surfaces, then such polyhedra may be classified into Prisms and Pyramids. Prism: A prism is a polyhedron having two equal and similar end faces called top face and bottom face (base) joined by other faces which may be Rectangles or Parallelograms. The imaginary line joining the centers of the faces is called the Axis. Top Face Longer edge Axis Rectangular Face Base Pyramids: A pyramid is a polyhedron having a plane figure for its base and equal number of isosceles triangular faces meeting at a point called Vertex or Apex.