A Theory of the IMF for Star Formation in Molecular Clouds
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

277 — 18 January 2016 Editor: Bo Reipurth ([email protected]) List of Contents
THE STAR FORMATION NEWSLETTER An electronic publication dedicated to early stellar/planetary evolution and molecular clouds No. 277 — 18 January 2016 Editor: Bo Reipurth ([email protected]) List of Contents The Star Formation Newsletter Interview ...................................... 3 Abstracts of Newly Accepted Papers ........... 5 Editor: Bo Reipurth [email protected] Abstracts of Newly Accepted Major Reviews . 30 Technical Editor: Eli Bressert Dissertation Abstracts ........................ 31 [email protected] New Jobs ..................................... 32 Technical Assistant: Hsi-Wei Yen Meetings ..................................... 33 [email protected] Summary of Upcoming Meetings ............. 36 Editorial Board Joao Alves Alan Boss Jerome Bouvier Cover Picture Lee Hartmann Thomas Henning The Rosette Nebula is a large HII region in Mono- Paul Ho ceros at a distance of about 1.6 - 1.7 kpc. It is Jes Jorgensen illuminated by the OB cluster NGC 2244, which Charles J. Lada contains seven O-stars, dominated by the O4V star Thijs Kouwenhoven HD 46223. The northwestern edge of the HII region Michael R. Meyer contains a large complex of globules and elephant Ralph Pudritz trunks. Luis Felipe Rodr´ıguez Ewine van Dishoeck Image courtesy Don Goldman http://astrodonimaging.com Hans Zinnecker ( ). The Star Formation Newsletter is a vehicle for fast distribution of information of interest for as- tronomers working on star and planet formation and molecular clouds. You can submit material for the following sections: Abstracts of recently Submitting your abstracts accepted papers (only for papers sent to refereed journals), Abstracts of recently accepted major re- Latex macros for submitting abstracts views (not standard conference contributions), Dis- and dissertation abstracts (by e-mail to sertation Abstracts (presenting abstracts of new [email protected]) are appended to Ph.D dissertations), Meetings (announcing meet- each Call for Abstracts. -

Formation of Massive Stars and Black Holes in Self-Gravitating AGN Discs
Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 1 November 2018 (MN LATEX style file v1.4) Formation of massive stars and black holes in self-gravitating AGN discs, and gravitational waves in LISA band. Yuri Levin1,2 (1)601 Campbell Hall, University of California, Berkeley, California, 94720 (2) Canadian Institute for Theoretical Astrophysics, University of Toronto, 60 St. George Street, Toronto, ON M5S 3H8, Canada printed 1 November 2018 ABSTRACT We propose a scenario in which massive stars form at the outer edges of an AGN accretion disc. We analyze the dynamics of a disc forming around a supermassive black hole, in which the angular momentum is transported by turbulence induced by the disc’s self-gravity. We find that once the surface density of the disc exceeds a critical value, the disc fragments into dense clumps. We argue that the clumps accrete material from the remaining disc and merge into larger clumps; the upper mass of a merged clump is a few tens to a few hundreds of solar mass. The biggest clumps collapse and form massive stars, which produce few-tens-solar-mass black holes at the end of their evolution. We construct a model of the AGN disc which includes extra heat sources from the embedded black holes. If the embedded black holes can accrete at the Bondi rate, then the feedback from accretion onto the embedded black holes may stabilize the AGN disc against the Toomre instability for an interesting range of the model parameters. By contrast, if the rate of accretion onto the embedded holes is below the Eddington limit, then the extra heating is insufficient to stabilize the disc. -

Interview with Peter Goldreich
PETER GOLDREICH (b. 1939) INTERVIEWED BY SHIRLEY K. COHEN March, April and November 1998 ARCHIVES CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California Preface to the LIGO Series Interviews The interview of Peter Goldreich (1998) was originally done as part of a series of 15 oral histories conducted by the Caltech Archives between 1996 and 2000 on the beginnings of the Laser Interferometer Gravitational-Wave Observatory (LIGO). Many of those interviews have already been made available in print form with the designation “The LIGO Interviews: Series I.” A second series of interviews was planned to begin after LIGO became operational (August 2002); however, current plans are to undertake Series II after the observatory’s improved version, known as Advanced LIGO, begins operations, which is expected in 2014. Some of the LIGO Series I interviews (with the “Series I” designation dropped) have now been placed online within Caltech’s digital repository, CODA. All Caltech interviews that cover LIGO, either exclusively or in part, will be indexed and keyworded for LIGO to enable online discovery. The original LIGO partnership was formed between Caltech and MIT. It was from the start the largest and most costly scientific project ever undertaken by Caltech. Today it has expanded into an international endeavor with partners in Europe, Japan, India, and Australia. As of this writing, 760 scientists from 11 countries are participating in the LSC—the LIGO Scientific Collaboration. http://resolver.caltech.edu/CaltechOH:OH_Goldreich_P Subject area Physics, geology, planetary science, astronomy, astrophysics, LIGO Abstract Interview in five sessions in March, April, and November 1998 with Peter Goldreich, Lee A. -

The Astronomy of Many Cultures: a Resource Guide
The Astronomy of Many Cultures: A Resource Guide by Andrew Fraknoi (Fromm Institute, U. of San Francisco) Version 5.1; July 2020 © copyright 2020 by Andrew Fraknoi. The right to use or reproduce this guide for any nonprofit educational purpose is hereby granted. For permission to use in other ways, or to suggest additional materials, please contact the author at e-mail: fraknoi {at} fhda {dot} edu The teaching of astronomy in our colleges and high schools often sidesteps the contributions of cultures outside of Europe and the U.S. white mainstream. Few educators (formal or informal) receive much training in this area, and they therefore tend to stick to people and histories they know from their own training -- even when an increasing number of their students or audiences might be from cultures beyond those familiar to them. Luckily, a wealth of material is becoming available to help celebrate the ideas and contributions of non-European cultures regarding our views of the universe. This listing of resources about cultures and astronomy makes no claim to be comprehensive, but simply consists of some English-language materials that can be used both by educators and their students or audiences. We include published and web-based materials, plus videos and classroom activities. In this edition, we have made a particular effort to enlarge resources about African-American and Hispanic American astronomers. Note that there’s a separate listing about the role of women in astronomy at: http://bit.ly/astronomywomen Table of Contents: 1. General Resources on the Astronomy of Diverse Cultures 2. -
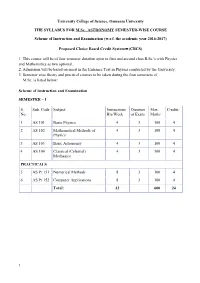
1 University College of Science, Osmania University THE
University College of Science, Osmania University THE SYLLABUS FOR M.Sc., ASTRONOMY SEMESTER-WISE COURSE Scheme of Instruction and Examination (w.e.f. the academic year 2016-2017) Proposed Choice Based Credit System – (CBCS) 1. This course will be of four semester duration open to first and second class B.Sc.'s with Physics and Mathematics as two optional. 2. Admission will be based on merit in the Entrance Test in Physics conducted by the University. 3. Semester wise theory and practical courses to be taken during the four semesters of M.Sc. is listed below: Scheme of Instruction and Examination SEMESTER – I S. Sub. Code Subject Instructions Duration Max. Credits No. Hrs/Week of Exam Marks 1 AS 101 Basic Physics 4 3 100 4 2 AS 102 Mathematical Methods of 4 3 100 4 Physics 3 AS 103 Basic Astronomy 4 3 100 4 4 AS 104 Classical (Celestial) 4 3 100 4 Mechanics PRACTICALS 5 AS Pr 151 Numerical Methods 8 3 100 4 6 AS Pr 152 Computer Applications 8 3 100 4 Total: 32 600 24 1 SEMESTER -II S. Sub. Code Subject Instructions Duration Max. Credits No. Hrs/Week of Exam Marks 1 AS 201 Quantum Mechanics 4 3 100 4 2 AS 202 Fluid Mechanics and Magneto 4 3 100 4 Hydro Dynamics 3 AS 203 Stellar Spectroscopy & 4 3 100 4 Atmosphere 4 AS 204 Stellar Structure & Evolution 4 3 100 4 PRACTICALS 5 AS Pr 251 Photometry & Spectroscopy 8 3 100 4 using IRAF and usage of Archival Data 6 AS Pr 252 Practical Astronomy 8 3 100 4 Total: 32 600 24 2 University College of Science, Osmania University THE SYLLABUS FOR M.Sc., ASTRONOMY SEMESTER-WISE COURSE Scheme of Instruction and Examination (w.e.f. -

Summer 2001 Volume 24 No. 2.Pdf
2:AI RA.NEWSLETTER Vhen these two methods are applied rc galaxies, we often lnside.,, find that the mass determined by the second method is Looking Up 3 several times as large as the visible mass determined by the Acknowledgement of ZOO0 Donors 4 first. Dynamical studies sugges t that this extra mass is not in Summer Sky 6 the disk of the galaxy where we find the bright stars and the gas and the dust, but is widely distributed in the surrounding halo, where we fin d relatively few stars. Srrpposing that it is always true that most of the matter in the halo is dark, then the halo of a galaxy like the Sombrero, where there are many This feature is inspired by the questions we baae receioed over the years fro* interested stars, should be exceedingly massive. \7e were therefore readers. If yow haoe a question'about an surprised to find that the total mass of the halo of the astronornical topic, please forward it to ws. Sombrero was quite ayerage. It must be that somethitg has happened in the halo which has caused the formation of an exceptionally large number of stars. This does not mean that Robert Hoyle asks: there is no dark matter. \We have seen only that the total mass Dear Dr. Shane: Your articles on the Sky in the Newsletter is quite normal but that a larger than normal fraction of this are always very interesting and particularly thought mass is in the form of halo stars. tMith regard to the total provokirg. -

Academia Sinica Institute of Astronomy and Astrophysics
Academia Sinica Institute of Astronomy and Astrophysics Letter from the Director Dear Colleagues and Friends: The establishment of the Preparatory Office of the Academia Sinica Institute of Astronomy and Astrophysics was proposed by Academician Chia-Chiao Lin, and approved in 1993 by the Academia Sinica with the support of Academy President Ta-You Wu. In the intervening years, our Institute has grown to be an exciting place in Asia to pursue research in astronomy and astrophysics, as we aspire to be competitive at the international level. In this brochure, we hope to convey to the readers a sampling of the kind of large projects which our Institute has been engaged in. Our emphasis has been on innovating forefront technology which will drive the progress in our discipline. We aim to choose our research initiatives carefully in order to concentrate our resources. The mission of our Institute has been to construct our own facilities, to gain access to advanced instruments, and to engage in research on fundamental astrophysical problems. Our staff members pursue a variety of scientific initiatives, ranging from planet formation to cosmology. We work on observational investigations across all wavelength bands, theoretical studies utilizing both analytical and numerical methods, and instrumentation projects in the radio, optical, and infrared windows. We offer herein some representative examples of the kind of exciting results which our young researchers have recently discovered. The success of our Institute has been guided by a succession of Directors, starting with Typhoon Lee, Chi Yuan, Kwok-Yung Lo, and Sun Kwok. We are grateful for the support of Academy President Yuan-Tseh Lee, and the guidance of our Advisory Panel chaired by Frank Shu. -

Indian Institute of Space Science and Technology
Indian Institute of Space Science and Technology Department of Space, Govt. of India Thiruvananthapuram Dual Degree Programme B.Tech in Engineering Physics with M.S. in Astronomy & Astrophysics or M.S. in Earth System Science or M.Tech in Optical Engineering or M.S. in Solid State Physics Curriculum and Syllabus Semester – I Code Title L T P C MA111 Calculus 3 1 0 4 PH111 Physics I 3 1 0 4 CH111 Chemistry 2 1 0 3 AE111 Introduction to Aerospace Engineering 3 0 0 3 AV111 Basic Electrical Engineering 3 0 0 3 HS111 Communication Skills 2 0 3 3 PH131 Physics Lab 0 0 3 1 AE131 Basic Engineering Lab 0 0 3 1 Total 16 3 9 22 Semester – II Code Title L T P C MA121 Vector Calculus and Differential Equations 2 1 0 3 MA122 Computer Programming and Applications 2 0 3 3 PH121 Physics II 3 1 0 4 CH121 Material Science and Metallurgy 3 0 0 3 AV121 Basic Electronics Engineering 3 0 0 3 AE141 Engineering Graphics 1 0 3 2 CH141 Chemistry Lab 0 0 3 1 AV141 Basic Electrical and Electronics Engineering Lab 0 0 3 1 Total 14 2 12 20 2 Semester – III Code Title L T P C MA211 Linear Algebra, Numerical Analysis and Transforms 3 0 0 3 PH211 Electrodynamics and Special Relativity 3 0 0 3 PH212 Mathematical Physics 3 1 0 4 AE215 Thermodynamics 3 0 0 3 AV215 Signals and Systems 3 1 0 4 HS211 Introduction to Economics 2 0 0 2 PH231 Optics Lab I 0 0 3 1 Total 17 1 3 20 Semester – IV Code Title L T P C Partial Differential Equations, Calculus of Variations MA221 3 0 0 3 and Complex Analysis PH221 Modern Optics 3 0 0 3 PH222 Classical Mechanics 3 1 0 4 AE225 Fluid Dynamics -

269 — 12 May 2015 Editor: Bo Reipurth ([email protected]) List of Contents
THE STAR FORMATION NEWSLETTER An electronic publication dedicated to early stellar/planetary evolution and molecular clouds No. 269 — 12 May 2015 Editor: Bo Reipurth ([email protected]) List of Contents The Star Formation Newsletter Interview ...................................... 3 My Favorite Object ............................ 8 Editor: Bo Reipurth [email protected] Perspective ................................... 12 Technical Editor: Eli Bressert Abstracts of Newly Accepted Papers .......... 17 [email protected] New Jobs ..................................... 42 Technical Assistant: Hsi-Wei Yen Meetings ..................................... 44 [email protected] Summary of Upcoming Meetings ............. 46 Editorial Board Short Announcements ........................ 48 Joao Alves Alan Boss Jerome Bouvier Lee Hartmann Cover Picture Thomas Henning Paul Ho The HII region on the cover is known as Sharp- Jes Jorgensen less 171, or W1, or NGC 7822. The young cluster Charles J. Lada Berkeley 59, seen in the upper left corner, contains Thijs Kouwenhoven a group of OB-stars at a distance of∼845 pc. The Michael R. Meyer cluster is sculpting the neutral gas into cometary Ralph Pudritz clouds and elephant trunks. North is left and east Luis Felipe Rodr´ıguez is down in this image. Ewine van Dishoeck Hans Zinnecker Image courtesy Neil Fleming http://flemingastrophotography.com The Star Formation Newsletter is a vehicle for fast distribution of information of interest for as- tronomers working on star and planet formation and -

Report for the Academic Years 1987-88 and 1988-89
Institute /or ADVANCED STUDY REPORT FOR THE ACADEMIC YEARS 1987-88 AND 1988-89 PRINCETON • NEW JERSEY nijiUfi.CAL ?""l::r"- £90"^ jr^^VTE LIBriARlf THE !f^;STiTUTE FQll AC -.MiEO STUDY PR1NCE70M, FmEW JEfiGcV 08540 AS3G TABLE OF CONTENTS 7 FOUNDERS, TRUSTEES AND OFFICERS OF THE BOARD AND OF THE CORPORATION 10 • OFFICERS OF THE ADMINISTRATION AND PROFESSOR AT LARGE 1 1 REPORT OF THE CHAIRMAN 14 REPORT OF THE DIRECTOR 1 ACKNOWLEDGMENTS 19 • FINANCIAL STATEMENTS AND INDEPENDENT AUDITORS' REPORT 32 REPORT OF THE SCHOOL OF HISTORICAL STUDIES ACADEMIC ACTIVITIES OF THE FACULTY MEMBERS, VISITORS AND RESEARCH STAFF 41 • REPORT OF THE SCHOOL OF MATHEMATICS ACADEMIC ACTIVITIES OF THE SCHOOL MEMBERS, VISITORS AND RESEARCH STAFF 51 REPORT OF THE SCHOOL OF NATURAL SCIENCES ACADEMIC ACTIVITIES OF THE FACULTY MEMBERS, VISITORS AND RESEARCH STAFF 58 • REPORT OF THE SCHOOL OF SOCIAL SCIENCE ACADEMIC ACTIVITIES OF THE SCHOOL AND ITS FACULTY MEMBERS, VISITORS AND RESEARCH STAFF 64 • REPORT OF THE INSTITUTE LIBRARIES 66 • RECORD OF INSTITUTE EVENTS IN THE ACADEMIC YEAR 1987 - 1988 86 • RECORD OF INSTITUTE EVENTS IN THE ACADEMIC YEAR 1988 - 1989 f:i'S^o FOUNDERS, TRUSTEES AND OFFICERS OF THE BOARD AND OF THE CORPORATION Foiifidcrs CAROLINE BAMBERGER FULD LOUIS BAMBERGER The Board of Trustees [1987-1989] MARELLA AGNELLI Turin, Italy [1988- ] THORNTON F. BRADSHAW New York, New York [deceased December 6, 1988] CHARLES L. BROWN Princeton, New Jersey FLETCHER L. BYROM Carefree, Arizona GLADYS K. DELMAS New York, New York [ -1988] MICHAEL V. FORRESTAL New York, New York [deceased January 11,1 989] MARVIN L. GOLDBERGER Director Institute for Advanced Study, Princeton, NewJersey VARTAN GREGORIAN President New York Public Library, New York, New York WILFRIED GUTH Chairman of the Supervisory Board Deutsche Bank AG, Frankfurt, Federal Republic of Germany RALPH E. -

Tezpur University
TEZPUR UNIVERSITY DEPARTMENT OF PHYSICS :: TEZPUR UNIVERSITY : TEZPUR: ASSAM M Sc Physics , 2009 Course Structure First Semester Course Course Name L T P CH CR Code PH-400 Physics Lab. - I 0 0 10 10 5 PH-401 Classical Mechanics – I 2 1 0 3 3 PH-402 Quantum Mechanics - I 2 1 0 3 3 PH-403 Mathematical Methods of Physics - I 2 1 0 3 3 PH-404 Electromagnetic Theory - I 2 1 0 3 3 PH-405 Semiconductor Devices 2 1 0 3 3 PH-413 Computational Techniques 2 0 2 4 3 Second Semester PH-407 Quantum Mechanics - II 2 1 0 3 3 PH-501 Condensed Matter Physics & Material Science - 2 1 0 3 3 I PH-503 Atomic & Molecular Physics 2 1 0 3 3 PH-410 Analog & Digital Electronics 2 1 2 5 4 PH-411 Statistical Physics 2 1 0 3 3 PH-499 Physics Lab. - II 0 0 10 10 5 Third Semester PH-500 Project Work - I 0 0 10 10 5 PH-409 Mathematical Methods of Physics - II 2 1 0 3 3 PH-415 Nuclear Theory & Particle Physics 2 1 0 3 3 PH-504 Laser Physics (E&P spl) 2 1 0 3 3 PH-522 Communication Systems (E&P spl) 2 1 0 3 3 PH-506 Physics of Thin Films (CMP spl) 2 1 0 3 3 PH-507 Physics of Low Temperature(CMP spl) 2 1 0 3 3 PH-519 Quantum Field Theory ( HE spl) 2 1 0 3 3 PH-521 Introduction to Parton Models ( HE spl) 2 1 0 3 3 PH-533 General Theory of Relativity 2 1 0 3 3 PH-536 Basic Astronomy and Astrophysics 2 1 0 3 3 Fourth Semester PH-509 Condensed Matter Physics & Materials Science - 2 1 0 3 3 II PH-510 Fibre Optics and Optoelectronics 2 1 0 3 3 PH-511 Image Processing 2 1 0 3 3 PH-512 Physics of Remote Sensing Technique 2 1 0 3 3 PH-513 Photonic Devices 2 1 0 3 3 PH-514 Superconductivity -

310 — 15 October 2018 Editor: Bo Reipurth ([email protected]) List of Contents
THE STAR FORMATION NEWSLETTER An electronic publication dedicated to early stellar/planetary evolution and molecular clouds No. 310 — 15 October 2018 Editor: Bo Reipurth ([email protected]) List of Contents The Star Formation Newsletter Interview ...................................... 3 My Favorite Object ............................ 6 Editor: Bo Reipurth [email protected] Abstracts of Newly Accepted Papers .......... 11 Associate Editor: Anna McLeod Dissertation Abstracts ........................ 43 [email protected] New Jobs ..................................... 44 Technical Editor: Hsi-Wei Yen Meetings ..................................... 45 [email protected] Summary of Upcoming Meetings ............. 47 Editorial Board Passings ...................................... 48 Joao Alves Alan Boss Jerome Bouvier Lee Hartmann Thomas Henning Cover Picture Paul Ho Jes Jorgensen In the giant molecular cloud that hosts the well Charles J. Lada known young cluster and HII region M17, Spitzer Thijs Kouwenhoven has found a dense dark cloud, M17SWex, which Michael R. Meyer is actively forming young stars. The image is a Ralph Pudritz composite of images from IRAC and MIPS, blue is Luis Felipe Rodr´ıguez 3.6 µm, green is 8 µm, and red is 24 µm. Ewine van Dishoeck Courtesy NASA/JPL-Caltech/M. Povich Hans Zinnecker The Star Formation Newsletter is a vehicle for fast distribution of information of interest for as- tronomers working on star and planet formation and molecular clouds. You can submit material Submitting your abstracts for the following sections: Abstracts of recently accepted papers (only for papers sent to refereed Latex macros for submitting abstracts journals), Abstracts of recently accepted major re- and dissertation abstracts (by e-mail to views (not standard conference contributions), Dis- [email protected]) are appended to sertation Abstracts (presenting abstracts of new each Call for Abstracts.