Young Et Al. (2015)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Iron Isotope Cosmochemistry Kun Wang Washington University in St
Washington University in St. Louis Washington University Open Scholarship All Theses and Dissertations (ETDs) 12-2-2013 Iron Isotope Cosmochemistry Kun Wang Washington University in St. Louis Follow this and additional works at: https://openscholarship.wustl.edu/etd Part of the Earth Sciences Commons Recommended Citation Wang, Kun, "Iron Isotope Cosmochemistry" (2013). All Theses and Dissertations (ETDs). 1189. https://openscholarship.wustl.edu/etd/1189 This Dissertation is brought to you for free and open access by Washington University Open Scholarship. It has been accepted for inclusion in All Theses and Dissertations (ETDs) by an authorized administrator of Washington University Open Scholarship. For more information, please contact [email protected]. WASHINGTON UNIVERSITY IN ST. LOUIS Department of Earth and Planetary Sciences Dissertation Examination Committee: Frédéric Moynier, Chair Thomas J. Bernatowicz Robert E. Criss Bruce Fegley, Jr. Christine Floss Bradley L. Jolliff Iron Isotope Cosmochemistry by Kun Wang A dissertation presented to the Graduate School of Arts and Sciences of Washington University in partial fulfillment of the requirements for the degree of Doctor of Philosophy December 2013 St. Louis, Missouri Copyright © 2013, Kun Wang All rights reserved. Table of Contents LIST OF FIGURES ....................................................................................................................... vi LIST OF TABLES ........................................................................................................................ -

74 Dauphas Et Al EPSL 2014.Pdf
Earth and Planetary Science Letters 398 (2014) 127–140 Contents lists available at ScienceDirect Earth and Planetary Science Letters www.elsevier.com/locate/epsl Magma redox and structural controls on iron isotope variations in Earth’s mantle and crust ∗ N. Dauphas a, , M. Roskosz b, E.E. Alp c, D.R. Neuville d,M.Y.Huc,C.K.Sioa, F.L.H. Tissot a, J. Zhao c, L. Tissandier e,E.Médardf,C.Cordierb a Origins Laboratory, Department of the Geophysical Sciences and Enrico Fermi Institute, The University of Chicago, 5734 South Ellis Avenue, Chicago, IL 60637, USA b Unité Matériaux et Transformations, Université Lille 1, CNRS UMR 8207, 59655 Villeneuve d’Ascq, France c Advanced Photon Source, Argonne National Laboratory, 9700 South Cass Avenue, Argonne, IL 60439, USA d Géochimie et Cosmochimie, IPGP-CNRS, Sorbonne Paris Cité, 1 rue Jussieu, 75005 Paris, France e Centre de Recherches Pétrographiques et Géochimiques, CNRS-UPR 2300, 15 rue Notre-Dame des Pauvres, BP20, 54501 Vandoeuvre-lès-Nancy, France f Laboratoire Magmas et Volcans, Université Blaise Pascal, CNRS, IRD, 5 rue Kessler, 63038 Clermont-Ferrand, France article info abstract Article history: The heavy iron isotopic composition of Earth’s crust relative to chondrites has been explained by Received 13 July 2013 vaporization during the Moon-forming impact, equilibrium partitioning between metal and silicate at Received in revised form 15 April 2014 core–mantle-boundary conditions, or partial melting and magma differentiation. The latter view is Accepted 21 April 2014 supported by the observed difference in the iron isotopic compositions of MORBS and peridotites. -
Odd Couple Decays Which Both One- and Two-Proton Decay Modes Juha Äystö Have Been Shown to Exist
19.1 N&V 273 MH 13/1/06 5:21 PM Page 279 NATURE|Vol 439|19 January 2006 NEWS & VIEWS NUCLEAR PHYSICS rather than sequential emission. As 94Ag was already known to undergo single-proton decay, Mukha and colleagues’ state is the first for Odd couple decays which both one- and two-proton decay modes Juha Äystö have been shown to exist. All previous studies of the two-proton decay The decay of proton-rich nuclei by the emission of a single proton has been of short-lived nuclear resonances from which known about for some time, and is well understood. The latest observation sequential decay is energetically possible have proved that these decays are indeed exclusively of two-proton emission, however, will provoke some head-scratching. sequential. Sequential emission is probably sup- pressed in 94Ag because the daugh- On page 298 of this issue1, Mukha ter state that is populated by the and colleagues report the simultane- Sn 50 first of two sequential decays would ous emission of two protons from a be an excited state of the palladium complex, long-lived state of the 94Ag isotope 93Pd. Rather than emitting silver isotope 94Ag, which has an a second proton, this state would odd number of protons. This type of tend to decay electromagnetically radioactive decay is expected only — by emitting a photon — to its for proton-rich nuclei with an even ground state. But why does the number of protons — so the obser- energetically unfavourable simulta- vation leaves nuclear physicists with neous two-proton decay itself some explaining to do. -
![Arxiv:1710.04254V5 [Astro-Ph.SR] 25 Jun 2019 Hr Xssawd Iest Nsei Se](https://docslib.b-cdn.net/cover/6203/arxiv-1710-04254v5-astro-ph-sr-25-jun-2019-hr-xssawd-iest-nsei-se-1946203.webp)
Arxiv:1710.04254V5 [Astro-Ph.SR] 25 Jun 2019 Hr Xssawd Iest Nsei Se
Accepted for publication in Astrophysical Journal Supplement, submitted on 19 September 2017, revised on 16 April 2018 Typeset using LATEX twocolumn style in AASTeX62 Explosive Nucleosynthesis in Near-Chandrasekhar Mass White Dwarf Models for Type Ia supernovae: Dependence on Model Parameters Shing-Chi Leung, Ken’ichi Nomoto1 1Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study The University of Tokyo, Kashiwa, Chiba 277-8583, Japan ABSTRACT We present two-dimensional hydrodynamics simulations of near-Chandrasekhar mass white dwarf (WD) models for Type Ia supernovae (SNe Ia) using the turbulent deflagration model with deflagration- detonation transition (DDT). We perform a parameter survey for 41 models to study the effects of the initial central density (i.e., WD mass), metallicity, flame shape, DDT criteria, and turbulent flame formula for a much wider parameter space than earlier studies. The final isotopic abundances of 11C to 91Tc in these simulations are obtained by post-process nucleosynthesis calculations. The survey includes SNe Ia models with the central density from 5 108 g cm−3 to 5 109 g cm−3 (WD masses × × of 1.30 - 1.38 M⊙), metallicity from 0 to 5 Z⊙, C/O mass ratio from 0.3 - 1.0 and ignition kernels including centered and off-centered ignition kernels. We present the yield tables of stable isotopes from 12C to 70Zn as well as the major radioactive isotopes for 33 models. Observational abundances of 55Mn, 56Fe, 57Fe and 58Ni obtained from the solar composition, well-observed SNe Ia and SN Ia remnants are used to constrain the explosion models and the supernova progenitor. -

Iron Isotope Systematics
Reviews in Mineralogy & Geochemistry Vol. 82 pp. XXX-XXX, 2017 11 Copyright © Mineralogical Society of America Iron Isotope Systematics Nicolas Dauphas Origins Lab Department of the Geophysical Sciences and Enrico Fermi Institute The University of Chicago 5734 South Ellis Avenue Chicago IL 60637 USA [email protected] Seth G. John University of Southern California Department of Earth Science Marine Trace Element Laboratory 3651 Trousdale Pkwy Los Angeles, CA 90089 USA [email protected] Olivier Rouxel IFREMER Department of Physical Resources and Deep-Sea Ecosystems Plouzané 29280 France University of Hawaii Department of Oceanography 1000 Pope Road Honolulu, HI 96822 USA [email protected] INTRODUCTION Iron is a ubiquitous element with a rich (i.e., complex) chemical behavior. It possesses three oxidation states, metallic iron (Fe0), ferrous iron (Fe2+) and ferric iron (Fe3+). The distribution of these oxidation states is markedly stratified in the Earth. • Metallic iron is primarily present in the core, where it is alloyed with Ni, Co, and light elements such as S, Si or O. Some metallic iron may be present at depth in the mantle because Fe2+ in bridgmanite can disproportionate into Fe3+ and Fe0 (Frost et al. 2004). Natural metallic iron also exists at the surface of the Earth in rare occurrences in the form of meteorite falls, metallic iron produced by reduction of lavas through interaction with coal sediments as in Disko Island (Greenland), and Josephinite (awaruite) produced by serpentinization reaction in peridotites. 1529-6466/17/0082-0011$10.00 http://dx.doi.org/10.2138/rmg.2017.82.11 Iron Isotope Systematics 277 • The main repository of ferrous iron is the mantle, where it is present in two spin states (the manner in which electrons fill the orbitals). -

High Precision Iron Isotope Measurements of Terrestrial and Lunar Materials
Geochimica et Cosmochimica Acta, Vol. 63, No. 11/12, pp. 1653–1660, 1999 Copyright © 1999 Elsevier Science Ltd Pergamon Printed in the USA. All rights reserved 0016-7037/99 $20.00 ϩ .00 PII S0016-7037(99)00089-7 High precision iron isotope measurements of terrestrial and lunar materials BRIAN L. BEARD* and CLARK M. JOHNSON Department of Geology and Geophysics, University of Wisconsin-Madison, Madison, Wisconsin 53706, USA (Received August 5, 1998; accepted in revised form February 11, 1999) Abstract—We present the analytical methods that have been developed for the first high-precision Fe isotope analyses that clearly identify naturally-occurring, mass-dependent isotope fractionation. A double-spike approach is used, which allows rigorous correction of instrumental mass fractionation. Based on 21 analyses of an ultra pure Fe standard, the external precision (1-SD) for measuring the isotopic composition of Fe is Ϯ0.14 ‰/mass; for demonstrated reproducibility on samples, this precision exceeds by at least an order of magnitude that of previous attempts to empirically control instrumentally-produced mass fractionation (Dixon et al., 1993). Using the double-spike method, 15 terrestrial igneous rocks that range in composition from peridotite to rhyolite, 5 high-Ti lunar basalts, 5 Fe-Mn nodules, and a banded iron formation have been analyzed for their iron isotopic composition. The terrestrial and lunar igneous rocks have the same isotopic compositions as the ultra pure Fe standard, providing a reference Fe isotope composition for the Earth and Moon. In contrast, Fe-Mn nodules and a sample of a banded iron formation have iron isotope compositions that vary over a relatively wide range, from ␦56Fe ϭϩ0.9 to Ϫ1.2 ‰; this range is 15 times the analytical errors of our technique. -

1 Excitation Functions and Isotopic Effects In
1 Excitation functions and isotopic effects in (n,p) reactions for stable iron isotopes from reaction threshold to 20 MeV. J. Joseph Jeremiah a, Damewan Suchiang b, B.M. Jyrwa a,* a Department of Physics, North Eastern Hill University, Shillong-793022, Meghalaya, India b Department of Physics, Tura Government College, Tura-794001, Meghalaya, India. * Corresponding Author. Email address : [email protected] (B.M. Jyrwa) Abstract The excitation functions for (n,p) reactions from reaction threshold to 20 MeV on four stable Iron isotopes viz; 54Fe,56Fe,57Fe and 58Fe were calculated using Talys-1.2 nuclear model code, this essentially involves fitting a set of global parameters. An excellent agreement between the calculated and experimental data is obtained with minimal effort on parameter fitting and only one free parameter called ‘Shell damping factor’ has been adjusted. This is very importance to the validation of nuclear model approaches with increased predictive power. The systematic decrease in (n, p) cross-sections with increasing neutron number in reactions induced by neutrons on isotopes of iron is explained in terms of the pre-equilibrium model. The compound nucleus and pre-equilibrium reaction mechanism as well as the isotopic effects were also studied extensively. Keywords Excitation functions, Shell damping factor, Compound nucleus model, Pre-equilibrium mechanism. 1. Introduction The common materials suitable for the reactor structures are stainless steel with Cr, Fe and Ni as main constituents. Structural materials are used to make the core and several other essential parts of a nuclear reactor. Thus, they must possess a high resistance to mechanical stress, stability to radiation and high temperature, and low neutron absorption. -

Iron and Nickel Isotope Measurements in Hibonite Using Chili L
79th Annual Meeting of the Meteoritical Society (2016) 6456.pdf IRON AND NICKEL ISOTOPE MEASUREMENTS IN HIBONITE USING CHILI L. Kööp1,2,4, T. Stephan1,2,4, A. M. Davis1,2,3,4, R. Trappitsch1,2, M. J. Pellin1,2,3,5, and P. R. Heck1,2,4, 1Department of the Geophysical Sciences, 2Chicago Center for Cosmochemistry, 3Enrico Fermi Institute, University of Chicago, Chicago, IL, 4Robert A. Pritzker Center for Meteoritics and Polar Studies, Field Museum of Natural History, Chica- go, IL, 5Materials Science Division, Argonne National Laboratory, Argonne, IL, E-mail: [email protected] Introduction: Hibonite-rich CAIs from CM chondrites have the largest nucleosynthetic anomalies of all materi- als believed to have formed inside the Solar System. In particular, these anomalies are found in the most neutron- rich isotopes of calcium and titanium, i.e., 48Ca and 50Ti (e.g., δ50Ti range is >300‰; [1–4]). These anomalies are believed to be the result of a heterogeneous distribution of material, originating from a rare type Ia supernova, in the early Solar System [1]. In these types of supernovae, neutron-rich isotopes of iron-peak elements are predicted to be efficiently produced alongside 48Ca and 50Ti, for example, 54Cr, 58Fe, 62Ni, and 64Ni [5]. This suggests that large iso- topic heterogeneities may have also existed in iron, chromium, and nickel when the Solar System formed, and traces of these may be preserved in hibonite-rich CAIs. This prediction has yet to be tested as the abundances of iron-peak elements in hibonite-rich CAIs are low, and abundant isobaric interferences exist that complicate analysis of these elements with conventional mass spectrometry. -

Iron Isotope Fractionation in Soils from Phenomena to Process Identification
Research Collection Doctoral Thesis Iron isotope fractionation in soils From phenomena to process identification Author(s): Wiederhold, Jan Georg Publication Date: 2006 Permanent Link: https://doi.org/10.3929/ethz-a-005275890 Rights / License: In Copyright - Non-Commercial Use Permitted This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library DISS. ETH NO. 16849 IRON ISOTOPE FRACTIONATION IN SOILS - FROM PHENOMENA TO PROCESS IDENTIFICATION Jan G. Wiederhold Zurich, 2006 DISS. ETH NO. 16849 IRON ISOTOPE FRACTIONATION IN SOILS - FROM PHENOMENA TO PROCESS IDENTIFICATION A dissertation submitted to ETH ZURICH for the degree of Doctor of Natural Sciences presented by JAN GEORG WIEDERHOLD Dipl.-Geoökol., University of Karlsruhe (TH) born 06.09.1975 citizen of Germany accepted on the recommendation of Prof. Dr. Ruben Kretzschmar, examiner PD Dr. Stephan M. Kraemer, co-examiner Dr. Nadya Teutsch, co-examiner Prof. Dr. Alex N. Halliday, co-examiner 2006 Und so sag ich zum letzten Male: Natur hat weder Kern noch Schale; Du prüfe dich nur allermeist, Ob du Kern oder Schale seist! And so for the last time this I tell: Nature has neither core nor shell; Better search yourself once more, Whether you are crust or core! Johann Wolfgang von Goethe, 1749-1832, German poet and natural scientist The iron oxide mineral goethite was named after him in 1815. III IV TABLE OF CONTENTS Summary VII Zusammenfassung IX 1. Introduction 1 1.1 Objectives and approach 3 2. Iron in soils 5 2.1 Pedogenic iron transformations 6 2.2 Dissolution of iron oxide minerals 11 References 14 3. -
![Arxiv:2004.00119V1 [Nucl-Ex]](https://docslib.b-cdn.net/cover/8083/arxiv-2004-00119v1-nucl-ex-3308083.webp)
Arxiv:2004.00119V1 [Nucl-Ex]
β-Decay Half-Lives of 55 Neutron-Rich Isotopes beyond the N=82 Shell Gap J. Wu,1, 2 S. Nishimura,2 P. M¨oller,3 M. R. Mumpower,4 R. Lozeva,5, 6 C. B. Moon,7 A. Odahara,8 H. Baba,2 F. Browne,9, 2 R. Daido,8 P. Doornenbal,2 Y. F. Fang,8 M. Haroon,8 T. Isobe,2 H. S. Jung,10 G. Lorusso,2, 11, 12 B. Moon,13 Z. Patel,12, 2 S. Rice,12, 2 H. Sakurai,2, 14 Y. Shimizu,2 L. Sinclair,15, 2 P.-A. S¨oderstr¨om,2 T. Sumikama,2 H. Watanabe,16, 2 Z. Y. Xu,17, 14 A. Yagi,8 R. Yokoyama,18 D. S. Ahn,2 F. L. Bello Garrote,19 J. M. Daugas,20 F. Didierjean,21 N. Fukuda,2 N. Inabe,2 T. Ishigaki,8 D. Kameda,2 I. Kojouharov,22 T. Komatsubara,2 T. Kubo,2 N. Kurz,22 K. Y. Kwon,23 S. Morimoto,8 D. Murai,2 H. Nishibata,8 H. Schaffner,22 T. M. Sprouse,24 H. Suzuki,2 H. Takeda,2 M. Tanaka,25 K. Tshoo,23 and Y. Wakabayashi2 1Physics Division, Argonne National Laboratory, Argonne, Illinois 60439, USA 2RIKEN Nishina Center, 2-1 Hirosawa, Wako-shi, Saitama 351-0198, Japan 3P. Moller Scientific Computing and Graphics, Inc., P. O. Box 1440, Los Alamos, NM 87544, USA 4Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA 5IPHC, IN2P3/CNRS, University of Strasbourg, F-67037 Strasbourg Cedex 2, France 6CSNSM, IN2P3/CNRS, University Paris-Saclay, F-91405 Orsay Campus, France 7Faculty of Science, Hoseo University, Chung-Nam 31499, Republic of Korea 8Department of Physics, Osaka University, Machikaneyama-machi 1-1, Osaka 560-0043 Toyonaka, Japan 9School of Computing, Engineering and Mathematics, University of Brighton, Brighton BN2 4GJ, United Kingdom 10Department of Physics, Chung-Ang University, Seoul 06974, Republic of Korea 11National Physical Laboratory, NPL, Teddington, Middlesex TW11 0LW, United Kingdom 12Department of Physics, University of Surrey, Guildford GU2 7XH, United Kingdom 13Department of Physics, Korea University, Seoul 02841, Republic of Korea 14Department of Physics, University of Tokyo, Hongo 7-3-1, Bunkyo-ku, 113-0033 Tokyo, Japan 15Department of Physics, University of York, Heslington, York, YO10 5DD, U.K. -
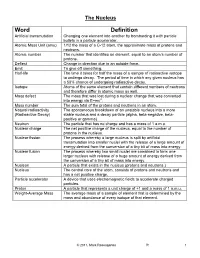
Word Definition Artificial Transmutation Changing One Element Into Another by Bombarding It with Particle Bullets in a Particle Accelerator
The Nucleus Word Definition Artificial transmutation Changing one element into another by bombarding it with particle bullets in a particle accelerator. Atomic Mass Unit (amu) 1/12 the mass of a C-12 atom, the approximate mass of protons and neutrons. Atomic number The number that identifies an element, equal to an atom’s number of protons. Deflect Change in direction due to an outside force. Emit To give off something. Half-life The time it takes for half the mass of a sample of radioactive isotope to undergo decay. The period of time in which any given nucleus has a 50% chance of undergoing radioactive decay. Isotope Atoms of the same element that contain different numbers of neutrons and therefore differ in atomic mass as well. Mass defect The mass that was lost during a nuclear change that was converted into energy via E=mc 2. Mass number The sum total of the protons and neutrons in an atom. Natural radioactivity The spontaneous breakdown of an unstable nucleus into a more (Radioactive Decay) stable nucleus and a decay particle (alpha, beta-negative, beta- positive or gamma). Neutron The particle that has no charge and has a mass of 1 a.m.u. Nuclear charge The net positive charge of the nucleus, equal to the number of protons in the nucleus. Nuclear fission The process whereby a large nucleus is split by artificial transmutation into smaller nuclei with the release of a large amount of energy derived from the conversion of a tiny bit of mass into energy. Nuclear fusion The process whereby two small nuclei are combined to form one larger nucleus with release of a huge amount of energy derived from the conversion of a tiny bit of mass into energy. -

Tracing Paleofluid Circulations Using Iron Isotopes: a Study of Hematite
Earth and Planetary Science Letters 254 (2007) 272–287 www.elsevier.com/locate/epsl Tracing paleofluid circulations using iron isotopes: A study of hematite and goethite concretions from the Navajo Sandstone (Utah, USA) ⁎ Vincent Busigny , Nicolas Dauphas Origins Laboratory, Department of the Geophysical Sciences and Enrico Fermi Institute, The University of Chicago, 5734 South Ellis Avenue, Chicago, IL 60637, USA The Field Museum, 1400 South Lake Shore Drive, Chicago, IL 60605, USA Received 18 December 2005; received in revised form 17 November 2006; accepted 20 November 2006 Available online 4 January 2007 Editor: C.P. Jaupart Abstract Iron concentrations and isotopic compositions were measured in spherical hematite and goethite concretions, together with associated red (Fe-oxide coated) and white (bleached) sandstones from the Jurassic Navajo formation, Utah (USA). Earlier studies showed that, in the Navajo Sandstone, reducing fluids (presumably rich in hydrocarbons) mobilized Fe present as Fe-oxide coatings on detrital quartz grains. Dissolved Fe then precipitated as spherical concretions by interaction with oxidizing groundwater. Despite being depleted in Fe by ∼50%, the bleached sandstones have Fe isotopic compositions similar to adjacent red sandstones (∼0‰/amu relative to IRMM-014). This shows that dissolution of Fe-oxide did not produce significant isotope fractionation, in agreement with previous experimental studies of abiotic Fe-oxide dissolution. In contrast, the concretions are depleted in the heavy isotopes of iron by −0.07 to −0.68‰/amu. This is opposite to the expected fractionation for partial Fe oxidation, which tends to enrich the precipitate in the heavy isotopes. Several scenarios are considered for explaining the measured Fe isotopic compositions.