Greg's Awesome Thesis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Genetic Analysis of Retinopathy in Type 1 Diabetes
Genetic Analysis of Retinopathy in Type 1 Diabetes by Sayed Mohsen Hosseini A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Institute of Medical Science University of Toronto © Copyright by S. Mohsen Hosseini 2014 Genetic Analysis of Retinopathy in Type 1 Diabetes Sayed Mohsen Hosseini Doctor of Philosophy Institute of Medical Science University of Toronto 2014 Abstract Diabetic retinopathy (DR) is a leading cause of blindness worldwide. Several lines of evidence suggest a genetic contribution to the risk of DR; however, no genetic variant has shown convincing association with DR in genome-wide association studies (GWAS). To identify common polymorphisms associated with DR, meta-GWAS were performed in three type 1 diabetes cohorts of White subjects: Diabetes Complications and Control Trial (DCCT, n=1304), Wisconsin Epidemiologic Study of Diabetic Retinopathy (WESDR, n=603) and Renin-Angiotensin System Study (RASS, n=239). Severe (SDR) and mild (MDR) retinopathy outcomes were defined based on repeated fundus photographs in each study graded for retinopathy severity on the Early Treatment Diabetic Retinopathy Study (ETDRS) scale. Multivariable models accounted for glycemia (measured by A1C), diabetes duration and other relevant covariates in the association analyses of additive genotypes with SDR and MDR. Fixed-effects meta- analysis was used to combine the results of GWAS performed separately in WESDR, ii RASS and subgroups of DCCT, defined by cohort and treatment group. Top association signals were prioritized for replication, based on previous supporting knowledge from the literature, followed by replication in three independent white T1D studies: Genesis-GeneDiab (n=502), Steno (n=936) and FinnDiane (n=2194). -

FBXO2 Antibody Cat
FBXO2 Antibody Cat. No.: 55-088 FBXO2 Antibody Western blot analysis in mouse brain tissue and HepG2,293 cell line lysates (35ug/lane). Specifications HOST SPECIES: Rabbit SPECIES REACTIVITY: Human, Mouse This FBXO2 antibody is generated from rabbits immunized with a KLH conjugated IMMUNOGEN: synthetic peptide between 244-271 amino acids from the C-terminal region of human FBXO2. TESTED APPLICATIONS: Flow, WB For FACS starting dilution is: 1:10~50 APPLICATIONS: For WB starting dilution is: 1:1000 PREDICTED MOLECULAR 33 kDa WEIGHT: September 24, 2021 1 https://www.prosci-inc.com/fbxo2-antibody-55-088.html Properties This antibody is purified through a protein A column, followed by peptide affinity PURIFICATION: purification. CLONALITY: Polyclonal ISOTYPE: Rabbit Ig CONJUGATE: Unconjugated PHYSICAL STATE: Liquid BUFFER: Supplied in PBS with 0.09% (W/V) sodium azide. CONCENTRATION: batch dependent Store at 4˚C for three months and -20˚C, stable for up to one year. As with all antibodies STORAGE CONDITIONS: care should be taken to avoid repeated freeze thaw cycles. Antibodies should not be exposed to prolonged high temperatures. Additional Info OFFICIAL SYMBOL: FBXO2 ALTERNATE NAMES: F-box only protein 2, FBXO2, FBX2 ACCESSION NO.: Q9UK22 PROTEIN GI NO.: 51338836 GENE ID: 26232 USER NOTE: Optimal dilutions for each application to be determined by the researcher. Background and References This gene encodes a member of the F-box protein family which is characterized by an approximately 40 amino acid motif, the F-box. The F-box proteins constitute one of the four subunits of the ubiquitin protein ligase complex called SCFs (SKP1-cullin-F-box), which function in phosphorylation-dependent ubiquitination. -

Molecular Genetic Analysis of Two Loci (Ity2 and Ity3) Involved in The
Copyright Ó 2007 by the Genetics Society of America DOI: 10.1534/genetics.107.075523 Molecular Genetic Analysis of Two Loci (Ity2 and Ity3) Involved in the Host Response to Infection With Salmonella Typhimurium Using Congenic Mice and Expression Profiling Vanessa Sancho-Shimizu,*,† Rabia Khan,*,† Serge Mostowy,† Line Larivie`re,† Rosalie Wilkinson,† Noe´mie Riendeau,† Marcel Behr† and Danielle Malo*,†,‡,1 *Department of Human Genetics, McGill University, Montreal, Quebec H3G 1A4, Canada and †Center for the Study of Host Resistance, McGill University Health Center, Montreal, Quebec H3G 1A4, Canada and ‡Department of Medicine, McGill University, Montreal, Quebec H3G 1A4, Canada Manuscript received May 4, 2007 Accepted for publication July 27, 2007 ABSTRACT Numerous genes have been identified to date that contribute to the host response to systemic Sal- monella Typhimurium infection in mice. We have previously identified two loci, Ity2 and Ity3, that control survival to Salmonella infection in the wild-derived inbred MOLF/Ei mouse using a (C57BL/6J 3 MOLF/ Ei)F2cross. We validated the existence of these two loci by creating congenic mice carrying each quan- titative trait locus (QTL) in isolation. Subcongenic mice generated for each locus allowed us to define the critical intervals underlying Ity2 and Ity3. Furthermore, expression profiling was carried out with the aim of identifying differentially expressed genes within the critical intervals as potential candidate genes. Genomewide expression arrays were used to interrogate expression differences in the Ity2 congenics, leading to the identification of a new candidate gene (Havcr2, hepatitis A virus cellular receptor 2). Interval-specific oligonucleotide arrays were created for Ity3, identifying one potential candidate gene (Chi3l1, chitinase 3-like 1) to be pursued further. -

CENPT (NM 025082) Human 3' UTR Clone – SC200995 | Origene
OriGene Technologies, Inc. 9620 Medical Center Drive, Ste 200 Rockville, MD 20850, US Phone: +1-888-267-4436 [email protected] EU: [email protected] CN: [email protected] Product datasheet for SC200995 CENPT (NM_025082) Human 3' UTR Clone Product data: Product Type: 3' UTR Clones Product Name: CENPT (NM_025082) Human 3' UTR Clone Vector: pMirTarget (PS100062) Symbol: CENPT Synonyms: C16orf56; CENP-T; SSMGA ACCN: NM_025082 Insert Size: 140 bp Insert Sequence: >SC200995 3’UTR clone of NM_025082 The sequence shown below is from the reference sequence of NM_025082. The complete sequence of this clone may contain minor differences, such as SNPs. Blue=Stop Codon Red=Cloning site GGCAAGTTGGACGCCCGCAAGATCCGCGAGATTCTCATTAAGGCCAAGAAGGGCGGAAAGATCGCCGTG TAACAATTGGCAGAGCTCAGAATTCAAGCGATCGCC AGTGGCAACTCTGTCTTCCCTGCCCAGTAGTGGCCAGGCTTCAACACTTTCCCTGTCCCCACCTGGGGA CTCTTGCCCCCACATATTTCTCCAGGTCTCCTCCCCACCCCCCCAGCATCAATAAAGTGTCATAAACAG AA ACGCGTAAGCGGCCGCGGCATCTAGATTCGAAGAAAATGACCGACCAAGCGACGCCCAACCTGCCATCA CGAGATTTCGATTCCACCGCCGCCTTCTATGAAAGG Restriction Sites: SgfI-MluI OTI Disclaimer: Our molecular clone sequence data has been matched to the sequence identifier above as a point of reference. Note that the complete sequence of this clone is largely the same as the reference sequence but may contain minor differences , e.g., single nucleotide polymorphisms (SNPs). RefSeq: NM_025082.4 Summary: The centromere is a specialized chromatin domain, present throughout the cell cycle, that acts as a platform on which the transient assembly of the kinetochore occurs during mitosis. All active centromeres are characterized by the presence of long arrays of nucleosomes in which CENPA (MIM 117139) replaces histone H3 (see MIM 601128). CENPT is an additional factor required for centromere assembly (Foltz et al., 2006 [PubMed 16622419]).[supplied by OMIM, Mar 2008] Locus ID: 80152 This product is to be used for laboratory only. Not for diagnostic or therapeutic use. -

ASSESSING DIAGNOSTIC and THERAPEUTIC TARGETS in OBESITY- ASSOCIATED LIVER DISEASES Noemí Cabré Casares
ASSESSING DIAGNOSTIC AND THERAPEUTIC TARGETS IN OBESITY- ASSOCIATED LIVER DISEASES Noemí Cabré Casares ADVERTIMENT. L'accés als continguts d'aquesta tesi doctoral i la seva utilització ha de respectar els drets de la persona autora. Pot ser utilitzada per a consulta o estudi personal, així com en activitats o materials d'investigació i docència en els termes establerts a l'art. 32 del Text Refós de la Llei de Propietat Intel·lectual (RDL 1/1996). Per altres utilitzacions es requereix l'autorització prèvia i expressa de la persona autora. En qualsevol cas, en la utilització dels seus continguts caldrà indicar de forma clara el nom i cognoms de la persona autora i el títol de la tesi doctoral. No s'autoritza la seva reproducció o altres formes d'explotació efectuades amb finalitats de lucre ni la seva comunicació pública des d'un lloc aliè al servei TDX. Tampoc s'autoritza la presentació del seu contingut en una finestra o marc aliè a TDX (framing). Aquesta reserva de drets afecta tant als continguts de la tesi com als seus resums i índexs. ADVERTENCIA. El acceso a los contenidos de esta tesis doctoral y su utilización debe respetar los derechos de la persona autora. Puede ser utilizada para consulta o estudio personal, así como en actividades o materiales de investigación y docencia en los términos establecidos en el art. 32 del Texto Refundido de la Ley de Propiedad Intelectual (RDL 1/1996). Para otros usos se requiere la autorización previa y expresa de la persona autora. En cualquier caso, en la utilización de sus contenidos se deberá indicar de forma clara el nombre y apellidos de la persona autora y el título de la tesis doctoral. -

Dissecting the Genetic Relationship Between Cardiovascular Risk Factors and Alzheimer's Disease
UC San Diego UC San Diego Previously Published Works Title Dissecting the genetic relationship between cardiovascular risk factors and Alzheimer's disease. Permalink https://escholarship.org/uc/item/7137q6g1 Journal Acta neuropathologica, 137(2) ISSN 0001-6322 Authors Broce, Iris J Tan, Chin Hong Fan, Chun Chieh et al. Publication Date 2019-02-01 DOI 10.1007/s00401-018-1928-6 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Acta Neuropathologica https://doi.org/10.1007/s00401-018-1928-6 ORIGINAL PAPER Dissecting the genetic relationship between cardiovascular risk factors and Alzheimer’s disease Iris J. Broce1 · Chin Hong Tan1,2 · Chun Chieh Fan3 · Iris Jansen4 · Jeanne E. Savage4 · Aree Witoelar5 · Natalie Wen6 · Christopher P. Hess1 · William P. Dillon1 · Christine M. Glastonbury1 · Maria Glymour7 · Jennifer S. Yokoyama8 · Fanny M. Elahi8 · Gil D. Rabinovici8 · Bruce L. Miller8 · Elizabeth C. Mormino9 · Reisa A. Sperling10,11 · David A. Bennett12 · Linda K. McEvoy13 · James B. Brewer13,14,15 · Howard H. Feldman14 · Bradley T. Hyman10 · Margaret Pericak‑Vance16 · Jonathan L. Haines17,18 · Lindsay A. Farrer19,20,21,22,23 · Richard Mayeux24,25,26 · Gerard D. Schellenberg27 · Kristine Yafe7,8,28 · Leo P. Sugrue1 · Anders M. Dale3,13,14 · Danielle Posthuma4 · Ole A. Andreassen5 · Celeste M. Karch6 · Rahul S. Desikan1 Received: 22 September 2018 / Revised: 28 October 2018 / Accepted: 28 October 2018 © Springer-Verlag GmbH Germany, part of Springer Nature 2018 Abstract Cardiovascular (CV)- and lifestyle-associated risk factors (RFs) are increasingly recognized as important for Alzheimer’s disease (AD) pathogenesis. Beyond the ε4 allele of apolipoprotein E (APOE), comparatively little is known about whether CV-associated genes also increase risk for AD. -

Role of Nlrs in the Regulation of Type I Interferon Signaling, Host Defense and Tolerance to Inflammation
International Journal of Molecular Sciences Review Role of NLRs in the Regulation of Type I Interferon Signaling, Host Defense and Tolerance to Inflammation Ioannis Kienes 1, Tanja Weidl 1, Nora Mirza 1, Mathias Chamaillard 2 and Thomas A. Kufer 1,* 1 Department of Immunology, Institute for Nutritional Medicine, University of Hohenheim, 70599 Stuttgart, Germany; [email protected] (I.K.); [email protected] (T.W.); [email protected] (N.M.) 2 University of Lille, Inserm, U1003, F-59000 Lille, France; [email protected] * Correspondence: [email protected] Abstract: Type I interferon signaling contributes to the development of innate and adaptive immune responses to either viruses, fungi, or bacteria. However, amplitude and timing of the interferon response is of utmost importance for preventing an underwhelming outcome, or tissue damage. While several pathogens evolved strategies for disturbing the quality of interferon signaling, there is growing evidence that this pathway can be regulated by several members of the Nod-like receptor (NLR) family, although the precise mechanism for most of these remains elusive. NLRs consist of a family of about 20 proteins in mammals, which are capable of sensing microbial products as well as endogenous signals related to tissue injury. Here we provide an overview of our current understanding of the function of those NLRs in type I interferon responses with a focus on viral infections. We discuss how NLR-mediated type I interferon regulation can influence the development of auto-immunity and the immune response to infection. Citation: Kienes, I.; Weidl, T.; Mirza, Keywords: NOD-like receptors; Interferons; innate immunity; immune regulation; type I interferon; N.; Chamaillard, M.; Kufer, T.A. -

C12) United States Patent (IO) Patent No.: US 10,774,349 B2 San Et Al
I1111111111111111 1111111111 111111111111111 IIIII IIIII IIIII IIIIII IIII IIII IIII US010774349B2 c12) United States Patent (IO) Patent No.: US 10,774,349 B2 San et al. (45) Date of Patent: Sep.15,2020 (54) ALPHA OMEGA BIFUNCTIONAL FATTY 9/1029 (2013.01); C12N 9/13 (2013.01); ACIDS C12N 9/16 (2013.01); C12N 9/88 (2013.01); C12N 9/93 (2013.01) (71) Applicant: William Marsh Rice University, (58) Field of Classification Search Houston, TX (US) None See application file for complete search history. (72) Inventors: Ka-Yiu San, Houston, TX (US); Dan Wang, Houston, TX (US) (56) References Cited (73) Assignee: William Marsh Rice University, U.S. PATENT DOCUMENTS Houston, TX (US) 9,994,881 B2 * 6/2018 Gonzalez . Cl2N 9/0006 2016/0090576 Al 3/2016 Garg et al. ( *) Notice: Subject to any disclaimer, the term ofthis patent is extended or adjusted under 35 FOREIGN PATENT DOCUMENTS U.S.C. 154(b) by 152 days. WO W02000075343 12/2000 (21) Appl. No.: 15/572,099 WO W02016179572 11/2016 (22) PCT Filed: May 7, 2016 OTHER PUBLICATIONS (86) PCT No.: PCT/US2016/031386 Choi, K. H., R. J. Heath, and C. 0. Rock. 2000. 13-Ketoacyl-acyl carrier protein synthase III (FabH) is a determining factor in § 371 (c)(l), branched-chain fatty acid biosynthesis. J. Bacteriol. 182:365-370. (2) Date: Nov. 6, 2017 He, X., and K. A. Reynolds. 2002. Purification, characterization, and identification of novel inhibitors of the beta-ketoacyl-acyl (87) PCT Pub. No.: WO2016/179572 carrier protein synthase III (FabH) from Staphylococcus aureus. -
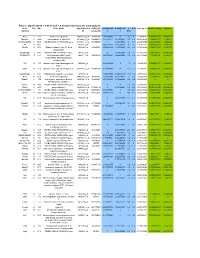
Table 2. Significant
Table 2. Significant (Q < 0.05 and |d | > 0.5) transcripts from the meta-analysis Gene Chr Mb Gene Name Affy ProbeSet cDNA_IDs d HAP/LAP d HAP/LAP d d IS Average d Ztest P values Q-value Symbol ID (study #5) 1 2 STS B2m 2 122 beta-2 microglobulin 1452428_a_at AI848245 1.75334941 4 3.2 4 3.2316485 1.07398E-09 5.69E-08 Man2b1 8 84.4 mannosidase 2, alpha B1 1416340_a_at H4049B01 3.75722111 3.87309653 2.1 1.6 2.84852656 5.32443E-07 1.58E-05 1110032A03Rik 9 50.9 RIKEN cDNA 1110032A03 gene 1417211_a_at H4035E05 4 1.66015788 4 1.7 2.82772795 2.94266E-05 0.000527 NA 9 48.5 --- 1456111_at 3.43701477 1.85785922 4 2 2.8237185 9.97969E-08 3.48E-06 Scn4b 9 45.3 Sodium channel, type IV, beta 1434008_at AI844796 3.79536664 1.63774235 3.3 2.3 2.75319499 1.48057E-08 6.21E-07 polypeptide Gadd45gip1 8 84.1 RIKEN cDNA 2310040G17 gene 1417619_at 4 3.38875643 1.4 2 2.69163229 8.84279E-06 0.0001904 BC056474 15 12.1 Mus musculus cDNA clone 1424117_at H3030A06 3.95752801 2.42838452 1.9 2.2 2.62132809 1.3344E-08 5.66E-07 MGC:67360 IMAGE:6823629, complete cds NA 4 153 guanine nucleotide binding protein, 1454696_at -3.46081884 -4 -1.3 -1.6 -2.6026947 8.58458E-05 0.0012617 beta 1 Gnb1 4 153 guanine nucleotide binding protein, 1417432_a_at H3094D02 -3.13334396 -4 -1.6 -1.7 -2.5946297 1.04542E-05 0.0002202 beta 1 Gadd45gip1 8 84.1 RAD23a homolog (S. -

Gene Knockdown of CENPA Reduces Sphere Forming Ability and Stemness of Glioblastoma Initiating Cells
Neuroepigenetics 7 (2016) 6–18 Contents lists available at ScienceDirect Neuroepigenetics journal homepage: www.elsevier.com/locate/nepig Gene knockdown of CENPA reduces sphere forming ability and stemness of glioblastoma initiating cells Jinan Behnan a,1, Zanina Grieg b,c,1, Mrinal Joel b,c, Ingunn Ramsness c, Biljana Stangeland a,b,⁎ a Department of Molecular Medicine, Institute of Basic Medical Sciences, The Medical Faculty, University of Oslo, Oslo, Norway b Norwegian Center for Stem Cell Research, Department of Immunology and Transfusion Medicine, Oslo University Hospital, Oslo, Norway c Vilhelm Magnus Laboratory for Neurosurgical Research, Institute for Surgical Research and Department of Neurosurgery, Oslo University Hospital, Oslo, Norway article info abstract Article history: CENPA is a centromere-associated variant of histone H3 implicated in numerous malignancies. However, the Received 20 May 2016 role of this protein in glioblastoma (GBM) has not been demonstrated. GBM is one of the most aggressive Received in revised form 23 July 2016 human cancers. GBM initiating cells (GICs), contained within these tumors are deemed to convey Accepted 2 August 2016 characteristics such as invasiveness and resistance to therapy. Therefore, there is a strong rationale for targeting these cells. We investigated the expression of CENPA and other centromeric proteins (CENPs) in Keywords: fi CENPA GICs, GBM and variety of other cell types and tissues. Bioinformatics analysis identi ed the gene signature: fi Centromeric proteins high_CENP(AEFNM)/low_CENP(BCTQ) whose expression correlated with signi cantly worse GBM patient Glioblastoma survival. GBM Knockdown of CENPA reduced sphere forming ability, proliferation and cell viability of GICs. We also Brain tumor detected significant reduction in the expression of stemness marker SOX2 and the proliferation marker Glioblastoma initiating cells and therapeutic Ki67. -

Role of NLRP3 Inflammasome Activation in Obesity-Mediated
International Journal of Environmental Research and Public Health Review Role of NLRP3 Inflammasome Activation in Obesity-Mediated Metabolic Disorders Kaiser Wani , Hind AlHarthi, Amani Alghamdi , Shaun Sabico and Nasser M. Al-Daghri * Biochemistry Department, College of Science, King Saud University, Riyadh 11451, Saudi Arabia; [email protected] (K.W.); [email protected] (H.A.); [email protected] (A.A.); [email protected] (S.S.) * Correspondence: [email protected]; Tel.: +966-14675939 Abstract: NLRP3 inflammasome is one of the multimeric protein complexes of the nucleotide-binding domain, leucine-rich repeat (NLR)-containing pyrin and HIN domain family (PYHIN). When ac- tivated, NLRP3 inflammasome triggers the release of pro-inflammatory interleukins (IL)-1β and IL-18, an essential step in innate immune response; however, defective checkpoints in inflamma- some activation may lead to autoimmune, autoinflammatory, and metabolic disorders. Among the consequences of NLRP3 inflammasome activation is systemic chronic low-grade inflammation, a cardinal feature of obesity and insulin resistance. Understanding the mechanisms involved in the regulation of NLRP3 inflammasome in adipose tissue may help in the development of specific inhibitors for the treatment and prevention of obesity-mediated metabolic diseases. In this narrative review, the current understanding of NLRP3 inflammasome activation and regulation is highlighted, including its putative roles in adipose tissue dysfunction and insulin resistance. Specific inhibitors of NLRP3 inflammasome activation which can potentially be used to treat metabolic disorders are also discussed. Keywords: NLRP3 inflammasome; metabolic stress; insulin resistance; diabetes; obesity Citation: Wani, K.; AlHarthi, H.; Alghamdi, A.; Sabico, S.; Al-Daghri, N.M. Role of NLRP3 Inflammasome 1. -

A Clinicopathological and Molecular Genetic Analysis of Low-Grade Glioma in Adults
A CLINICOPATHOLOGICAL AND MOLECULAR GENETIC ANALYSIS OF LOW-GRADE GLIOMA IN ADULTS Presented by ANUSHREE SINGH MSc A thesis submitted in partial fulfilment of the requirements of the University of Wolverhampton for the degree of Doctor of Philosophy Brain Tumour Research Centre Research Institute in Healthcare Sciences Faculty of Science and Engineering University of Wolverhampton November 2014 i DECLARATION This work or any part thereof has not previously been presented in any form to the University or to any other body whether for the purposes of assessment, publication or for any other purpose (unless otherwise indicated). Save for any express acknowledgments, references and/or bibliographies cited in the work, I confirm that the intellectual content of the work is the result of my own efforts and of no other person. The right of Anushree Singh to be identified as author of this work is asserted in accordance with ss.77 and 78 of the Copyright, Designs and Patents Act 1988. At this date copyright is owned by the author. Signature: Anushree Date: 30th November 2014 ii ABSTRACT The aim of the study was to identify molecular markers that can determine progression of low grade glioma. This was done using various approaches such as IDH1 and IDH2 mutation analysis, MGMT methylation analysis, copy number analysis using array comparative genomic hybridisation and identification of differentially expressed miRNAs using miRNA microarray analysis. IDH1 mutation was present at a frequency of 71% in low grade glioma and was identified as an independent marker for improved OS in a multivariate analysis, which confirms the previous findings in low grade glioma studies.