DOCSLIB.ORG

The Evolution of Recombination and Genomic Structures: a Modeling Approach

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Evolution of Recombination and Genomic Structures: a Modeling Approach The evolution of recombination and genomic structures: a modeling approach. Alexandra Popa To cite this version: Alexandra Popa. The evolution of recombination and genomic structures: a modeling approach.. Bioinformatics [q-bio.QM]. Université Claude Bernard - Lyon I, 2011. English. tel-00750370 HAL Id: tel-00750370 https://tel.archives-ouvertes.fr/tel-00750370 Submitted on 9 Nov 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. N◦ d'ordre: Ann´ee2011 THESE pr´esent´ee devant l'UNIVERSITE CLAUDE BERNARD - LYON I pour l'obtention du DIPLOME DE DOCTORAT (arr^et´edu 7 ao^ut 2006) par Alexandra Mariela POPA The evolution of recombination and genomic structures: a modeling approach. Directeur de th`ese: Christian GAUTIER Co-directrice de th`ese: Dominique MOUCHIROUD JURY: Laurent DURET Pr´esident du jury Christian GAUTIER Directeur Sylvain GLEMIN Rapporteur Christine MEZARD Rapporteur Dominique MOUCHIROUD Directrice Matthew WEBSTER Rapporteur ii UNIVERSITE CLAUDE BERNARD - LYON 1 Président de l’Université M. A. Bonmartin Vice-président du Conseil d’Administration M. le Professeur G. Annat Vice-président du Conseil des Etudes et de la Vie Universitaire M. le Professeur D. Simon Vice-président du Conseil Scientifique M. le Professeur J-F. Mornex Secrétaire Général M. G. Gay COMPOSANTES SANTE Faculté de Médecine Lyon Est – Claude Bernard Directeur : M. le Professeur J. Etienne Faculté de Médecine et de Maïeutique Lyon Sud – Charles Directeur : M. le Professeur F-N. Gilly Mérieux UFR d’Odontologie Directeur : M. le Professeur D. Bourgeois Institut des Sciences Pharmaceutiques et Biologiques Directeur : M. le Professeur F. Locher Institut des Sciences et Techniques de la Réadaptation Directeur : M. le Professeur Y. Matillon Département de formation et Centre de Recherche en Biologie Directeur : M. le Professeur P. Farge Humaine COMPOSANTES ET DEPARTEMENTS DE SCIENCES ET TECHNOLOGIE Faculté des Sciences et Technologies Directeur : M. le Professeur F. Gieres Département Biologie Directeur : M. le Professeur F. Fleury Département Chimie Biochimie Directeur : Mme le Professeur H. Parrot Département GEP Directeur : M. N. Siauve Département Informatique Directeur : M. le Professeur S. Akkouche Département Mathématiques Directeur : M. le Professeur A. Goldman Département Mécanique Directeur : M. le Professeur H. Ben Hadid Département Physique Directeur : Mme S. Fleck Département Sciences de la Terre Directeur : Mme le Professeur I. Daniel UFR Sciences et Techniques des Activités Physiques et Sportives Directeur : M. C. Collignon Observatoire de Lyon Directeur : M. B. Guiderdoni Ecole Polytechnique Universitaire de Lyon 1 Directeur : M. P. Fournier Ecole Supérieure de Chimie Physique Electronique Directeur : M. G. Pignault Institut Universitaire de Technologie de Lyon 1 Directeur : M. le Professeur C. Coulet Institut de Science Financière et d'Assurances Directeur : M. le Professeur J-C. Augros Institut Universitaire de Formation des Maîtres Directeur : M. R. Bernard 2 iii Abstract Meiotic recombination plays several critical roles in molecular evolution. First, recombina- tion represents a key step in the production and transmission of gametes during meiosis. Second, recombination facilitates the impact of natural selection by shuffling genomic sequences. Furthermore, the action of certain repair mechanisms during recombination affects the frequencies of alleles in populations via biased gene conversion. Lately, the numerous advancements in the study of recombination have unraveled the complexity of this process regarding both its mechanisms and evolution. The main aim of this thesis is to analyze the relationships between the different causes, characteristics, and effects of recombination from an evolutionary perspective. First, we developed a model based on the control mechanisms of meiosis and inter-crossover interference. We further used this model to compare the recombination strategies in multiple vertebrates and invertebrates, as well as between sexes. Second, we studied the impact of the sex-specific localization of recombination hotspots on the evolution of the GC content for several vertebrates. Last, we built a population genetics model to analyze the impact of recombination on the frequency of deleterious mutation in the human population. R´esum´e La recombinaison m´eiotique joue un double r^ole de moteur ´evolutif en participant `ala cr´eation d'une diversit´eg´en´etique soumise `ala s´election naturelle et de contr^ole dans la fabrication des gam`etes lors de la m´eiose. De plus, en association avec certains m´ecanismes de r´eparation, la recombinaison, au travers de la conversion g´enique biais´eemanipule les fr´equences all´eliques au sein des populations. Les connaissances sur le fonctionnement m^eme des ce processus ont consid´erablement augment´ees ces derni`eres ann´ees faisant d´ecouvrir un processus complexe, autant dans son fonctionnement que dans son ´evolution. Le th`eme g´en´eral de la th`eseest l'analyse, dans un contexte ´evolutif, des relations entre les diff´erent r^oles et caract´eristiques fonctionnelles de la recombinaison. Un mod`ele de la recombinaison prenant en compte des contraintes li´eesau contr^ole de la m´eiose et le ph´enom`ene d'interf´erence a permis une comparaison entre esp`ecesau sein des vert´ebr´es et des invert´ebr´esde m^eme qu'un comparaison entre sexes. Par ailleurs, nous avons montr´el'impact de la localisation sp´ecifique aux sexes des points chauds de recombinaison sur l'´evolution du contenu en GC des g´enomes de plusieurs vert´ebr´es. Finalement, nous proposons un mod`ele `al'´echelle de la g´en´etique des populations, permettant d'analyser l'impact de la recombinaison sur la fr´equences de mutations d´el´et`eres dans les populations humaines. Cette th`ese,nous l'esp´erons, apportera sa pierre `al'´etude interdisciplinaire de la recombinaison, `ala fois au sein de la biologie et par ses relations au travers de la mod´elisation avec l'informatique et les math´ematiques. iv Notations General abbreviations A Adenine bp base pair C Cytosine CpG A dinucleotide CG, p standing for a phosphate link. DNA Deoxyribonucleic acid G Guanine Gb Giga base kb kilo base Mb Mega base Myr Million years Ne effective population size SNP single nucleotide polymorphism T Thymine TSS Transcription Start Site Meiosis and recombination-related abbreviations CE Central Element (referring to the SC) cM centimorgan CO Crossover COI CO Interference COR Crossover Rate dHJ double Holliday Junction DSB Double-Strand Break DSBh Double-Strand Break hotspot DSBR Double-Strand Break Repair model dsDNA double stranded DNA F1 First generation of offspring in a crossing experiment F2 Second generation of offspring in a crossing experiment F/M Female/Male ratio HapMap1, 2, and 3 the 1st, 2nd, and 3rd respective phases of HapMap Project HJ Holliday Junction HR Homologous Recombination v vi HS Heterogeneous Stock (for mouse populations) LD Linkage Disequilibrium LE Lateral Element (referring to the SC) NAHR Nonallelic Homologous Recombination NCO Non-crossover NCOR Non-crossover Rate NE Nuclear Envelope NHEJ Nonhomologous End Joining PC Pairing Centres rDNA ribosomal DNA RI Recombinant Inbred lines (in a crossing experiment) SC Synaptonemal Complex SDSA Synthesis-Dependent Strand-Annealing model SEI Single End Invasion ssDNA single stranded DNA TF Transverse Filaments (referring to the SC) Mathematical symbols C coefficient of coincidence C3 Three-point coefficient of coincidence. D0 the difference between the frequency of a two locus haplotype and the product of the component alleles, divided by the most extreme possible value, given the marginal allele frequencies, measure of LD g genetic distance I Identity matrix m In the counting models, m stands for the number of NCO events that separate two consecutive COs. It is a measure of the strength of interference P Physical length (Mb) of an interval or chromosome p The fraction of COs that are not subject to interference under the two-pathway model Housworth and Stahl (2003). Q the substitution matrix along a branch of a phylogenetic tree R frequency of recombinants among the offspring r2 correlation of alleles at different loci, measure of LD y The mean number of DSB events in the counting model of Foss et al. (1993). # Number χ2 Chi-square distribution Γ Gamma distribution λ The rate parameter for Γ ν The shape parameter for Γ vii σ0 Uniform basal tensile stress in the mechanical stress model of Kleckner et al. (2004). ⊗ Tensor product of matrices BGC abbreviations BGC Biased Gene Conversion BER base excision repair gBGC GC Biased Gene Conversion GC* equilibrium or stationary GC-content MMR mismatch repair Other abbreviations AIC Akaike Information Criterion BIC Bayesian Information Criterion CEPH Centre d'Etude du Polymorphism Humain CI Confidence Interval DAF Derived Allele Frequency DT Distance to Telomeres HGMD Human Gene Mutation Database H-W test Hotteling-William's t-test L Likelihood LCR Low Copy Repeat LDT Log Distance to Telomeres LINE Long interspersed nuclear element LOD Logarithm of Odds MHC Major Histocompatibility Complex PAR Pseudoautosomal Region PCR Polymerase Chain Reaction RE Repetitive Element SINE Short Interspersed Nuclear Element TE Transposable Element viii Definitions Information assembled from Stumpf and McVean (2003); Arnheim et al. (2007); Lynch (2007); Paigen and Petkov (2010); DB-NCBI Allele One of the variant forms of a DNA sequence at a particular locus, or location, on a chromosome. Backcross Crossing experiment in which individuals in the first generation are crossed back with one or both their parents to obtain the second generation of offspring. Bouquet formation The clustering of telomeres together on the nuclear membrane early in meiosis.
Load more

Recommended publications
  • Laboratory III Linkage
    Genetics Laboratory III Biology 303 Spring 2007 Linkage Dr. Wadsworth Introduction same chromosome, the meiotic assortment of chromosomes alone would not predict the Genes are arranged as units in a linear order independent assortment of genes on those along chromosomes. The position of each gene chromosomes. In the absence of gene along the chromosome is called its locus. Each assortment, we would predict that the progeny gene has a unique chromosomal position and could only have the allelic combinations that therefore a unique locus. In fact, geneticists were present in the parent chromosomes. Genes often use the term genetic locus interchangeably that do not assort are said to show complete with the term gene. linkage. Alternatively, genes that independently assort are said to be unlinked. For the following The relative position of genes along a two examples, compare the genotypes and chromsomes can be analyzed by determining phenotypes generated in a dihybrid crosses of their linkage relationship. The concept of unlinked and completely linked genes. genetic linkage is outlined in this handout and will be discussed in class in the coming weeks. The position of a gene on a chromosome can be Example 1: A dihybrid cross for genes A and B, establish its identity. two unlinked genes. Generation Genotypes Phenotypes Specific Goals P1 AABBXaabb AB and ab 1. Conduct appropriate genetic crosses with a F1 AaBb AB mutant D. melanogaster to determine the following: F2 1AABB:2AABb: 9AB:3Ab:3aB:1ab 2AaBB:4AaBb:1AAbb: 2Aabb:1aaBB:2aaBb:1aabb a. Segregation b. Independent Assortment/Linkage Phenotypic ratio from dihybrid cross for c.
    [Show full text]
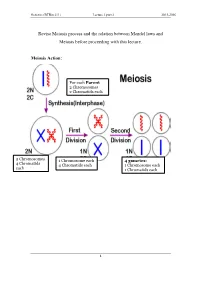
  • Revise Meiosis Process and the Relation Between Mendel Laws and Meiosis Before Proceeding with This Lecture
    Genetics (BTBio 211) Lecture 3 part 2 2015-2016 Revise Meiosis process and the relation between Mendel laws and Meiosis before proceeding with this lecture. Meiosis Action: For each Parent 2 Chromosomes 2 Chromatids each 2 Chromosomes 1 Chromosome each 4 gametes: 4 Chromatid s 4 Chromatids each 1 Chromosome each each 1 Chromatids each 1 Genetics (BTBio 211) Lecture 3 part 2 2015-2016 LINKAGE AND CHROMOSOME MAPPING IN EUKARYOTES I. LINKAGE Genetic linkage is the tendency of genes that are located proximal to each other on a chromosome to be inherited together during meiosis. Genes whose loci are nearer to each other are less likely to be separated onto different chromatids during chromosomal crossover, and are therefore said to be genetically linked. Linked genes: Genes that are inherited together with other gene(s) in form of single unit as they are located on the same chromosome. For example: in fruit flies the genes for eye color and the genes for wing length are on the same chromosome, thus are inherited together. A couple of genes on chromosomes may be present either on the different or on the same chromosome. 1. The independent assortment of two genes located on different chromosomes. Mendel’s Law of Independent Assortment: during gamete formation, segregation of one gene pair is independent of other gene pairs because the traits he studied were determined by genes on different chromosomes. Consider two genes A and B, each with two alleles A a and B b on separate (different) chromosomes. 2 Genetics (BTBio 211) Lecture 3 part 2 2015-2016 Gametes of non-homologous chromosomes assort independently at anaphase producing 4 different genotypes AB, ab, Ab and aB with a genotypic ratio 1:1:1:1.
    [Show full text]
  • Issue 85 of the Genetics Society Newsletter
    JULY 2021 | ISSUE 85 GENETICS SOCIETY NEWS In this issue The Genetics Society News is edited by • Presidential handover Margherita Colucci and items for future • Genetics Society Summer Studentship - Share your story, Part 1 issues can be sent to the editor by email • A chat with Dr Stuart Ritchie - Exploring “Science fictions” to [email protected]. • Committee on Mutagenicity of Chemicals in Food, Consumer The Newsletter is published twice a year, Products and the Environment (COM) with copy dates of July and January. • How genetic linkage was discovered Genetics Society Summer Studentship - Share your stories, Part 1. Read the interviews on page 27 A WORD FROM THE EDITOR A word from the editor Welcome to Issue 85 elcome to the latest issue of the world that cry for change: with WGenetics Society Newsletter! Dr Stuart Ritchie, we explore In this issue, “change” is the keyword. misconduct and fraud in science and the solutions that “open science” Through a series of interviews, we proposes, talking about his latest explored the changes from their book “Science fictions: how fraud, undergraduate role and the career bias, negligence and hype undermine evolution of the past years Summer the search for truth”. Studentship grant winners. Where are they now? What impact that research I would like to draw your attention experience had on them? Find out to the opportunity of contributing more in “Genetics Society Summer to the special issue of Heredity. In Studentship - Share your story, July 2022, this special issue will be Part 1”, page 23. celebrating Mendel’s 200th birthday with short essays, reviews and Big changes happened in the Society research articles on “exceptions” too.
    [Show full text]
  • Linkage, Recombination, and Eukaryotic Gene Mapping 163
    Linkage, Recombination, 7 and Eukaryotic Gene Mapping LINKED GENES AND BALD HEADS or many, baldness is the curse of manhood. Twenty-five Fpercent of men begin balding by age 30 and almost half are bald to some degree by age 50. In the United States, baldness affects more than 40 million men, who spend hundreds of mil- lions of dollars each year on hair-loss treatment. Baldness is not just a matter of vanity: bald males are more likely to suffer from heart disease, high blood pressure, and prostate cancer. Baldness can arise for a number of different reasons, including illness, injury, drugs, and heredity. The most-com- mon type of baldness seen in men is pattern baldness—techni- cally known as androgenic alopecia—in which hair is lost pre- (a) (b) maturely from the front and top of the head. More than 95% of hair loss in men is pattern baldness. Although pattern bald- ness is also seen in women, it is usually expressed weakly as mild thinning of the hair. The trait is clearly stimulated by male Pattern baldness is a hereditary trait. sex hormones (androgens), as evidenced by the observation Recent research demonstrated that a gene that males castrated at an early age rarely become bald (but this for pattern baldness is linked to genetic markers located on the X chromosome, is not recommended as a preventive treatment for baldness). leading to the discovery that pattern A strong hereditary influence on pattern baldness has long baldness is influenced by variation in the been recognized, but the exact mode of inheritance has been androgen-receptor gene.
    [Show full text]
  • William Ernest Castle
    NATIONAL ACADEMY OF SCIENCES WILLIAM ERNEST C ASTLE 1867—1962 A Biographical Memoir by L . C . D UNN Any opinions expressed in this memoir are those of the author(s) and do not necessarily reflect the views of the National Academy of Sciences. Biographical Memoir COPYRIGHT 1965 NATIONAL ACADEMY OF SCIENCES WASHINGTON D.C. WILLIAM ERNEST CASTLE October 25,1861-June 3,1962 BY L. C. DUNN HE LIFE OF William Ernest Castle was so intimately con- Tnected with the development of the science of genetics in the United States that an account of his scientific career is also a story of the early years of genetics in this country. His sci- entific lifetime included the period from the rediscovery of Mendel's laws in 1900 until 1961 when his last paper on in- heritance of coat color in horses was published. For all these years he devoted himself exclusively to this field—as an ex- ponent and pioneer of the methods and views introduced by Mendel, as a research worker who with his students established the field of mammalian genetics, and as one of the first univer- sity teachers of genetics whose students became university teachers and themselves begat other generations of Castle's in- tellectual descendants. In all of this he spoke in direct and sim- ple terms to a wide audience, attracted to the new science by its potential usefulness in agriculture, in medical and social prob- lems, and especially in the interpretation of the mechanism of evolution. In fact, before the introduction of the term "genetics" by William Bateson in 1906, Castle referred to the A chronology of Castle's life is appended to this memoir together with a bibliography of his writings.
    [Show full text]
  • Discovery of the Sex-Linked Traits. in 1910, Morgan Published Details of His Research in an Article Titled “Sex Limited Inheritance in Drosophila"
    Lecture 4. Chromosome theory of inheritance. Sex determination and the inheritance of sex-linked traits. 1. Chromosome theory of inheritance. 2. Chromosome mapping. 3. Sex determination and the inheritance of sex-linked traits. In 1865 Gregor Mendel has discovered laws of heredity. But he came to the conclusion of the heredity principles without the knowledge of genes and chromosomes. Over the next decades after Mendel’s findings cytological bases of heredity become more understandable. In 1869 Johannes Friedrich Miescher was the first researcher to isolate and identify nucleic acid in pus cells. In 1878 Walther Flemming described chromatin threads in cell nucleus and behavior of chromosomes during mitosis. In 1890 August Weismann described role of meiosis for reproduction and heredity. In 1888 Heinrich Waldeyer has coined the term “chromosome” to describe basophilic stained filaments inside the cell nucleus. The speculation that chromosomes might be the key to understanding heredity led several scientists to examine Mendel’s publications and re- evaluate his model in terms of the behavior of chromosomes during mitosis and meiosis. In 1902, Theodor Boveri (right) observed that proper embryonic development of sea urchins does not occur unless chromosomes are present. That same year, Walter Sutton (left) observed the separation of chromosomes into daughter cells during meiosis. Together, these observations led to the development of the Chromosomal Theory of Inheritance, which identified chromosomes as the genetic material responsible for Mendelian inheritance. The Chromosomal Theory of Inheritance was consistent with Mendel’s laws and was supported by the following observations: During meiosis, homologous chromosome pairs migrate as discrete structures that are independent of other chromosome pairs.
    [Show full text]
  • 7 Linkage, Recombination, and Eukaryotic Gene Mapping
    Linkage, Recombination, and 7 Eukaryotic Gene Mapping • Alfred Sturtevant and the First Genetic Map • Genes That Assort Independently and Those That Don’t • Linkage and Recombination Between Two Genes Notation for Crosses with Linkage Complete Linkage Compared with Independent Assortment Crossing Over with Linked Genes Calculation of Recombination Frequency Coupling and Repulsion The Physical Basis of Recombination Predicting the Outcome of Crosses with Linked Genes Testing for Independent Assortment Gene Mapping with Recombination Frequencies Constructing a Genetic Map with Two-Point Testcrosses • Linkage and Recombination Between Three Genes Gene Mapping with the Three-Point Testcross Alfred Henry Sturtevant, an early geneticist, developed the first genetic map. (Institute Archives, California Institute of Technology.) Gene Mapping in Humans Mapping with Molecular Markers • Physical Chromosome Mapping Deletion Mapping Somatic-Cell Hybridization In Situ Hybridization Alfred Sturtevant Mapping by DNA Sequencing and the First Genetic Map In 1909, Thomas Hunt Morgan taught the introduction to Morgan’s other research students virtually lived in the labo- zoology class at Columbia University. Seated in the lecture ratory, raising fruit flies, designing experiments, and dis- hall were sophomore Alfred Henry Sturtevant and freshman cussing their results. Calvin Bridges. Sturtevant and Bridges were excited In the course of their research, Morgan and his stu- by Morgan’s teaching style and intrigued by his interest in dents observed that some pairs of genes did not segregate biological problems. They asked Morgan if they could work randomly according to Mendel’s principle of independent in his laboratory and, the following year, both young men assortment but instead tended to be inherited together.
    [Show full text]
  • The Birth of Classical Genetics As the Junction of Two Disciplines: Conceptual Change As Representational Change Marion Vorms
    The birth of classical genetics as the junction of two disciplines: conceptual change as representational change Marion Vorms To cite this version: Marion Vorms. The birth of classical genetics as the junction of two disciplines: conceptual change as representational change. Studies in History and Philosophy of Science Part A, Elsevier, 2014, 48, pp.105-116. 10.1016/j.shpsa.2014.05.007. halshs-01122308 HAL Id: halshs-01122308 https://halshs.archives-ouvertes.fr/halshs-01122308 Submitted on 7 Jun 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THE BIRTH OF CLASSICAL GENETICS AS THE JUNCTION OF TWO DISCI- PLINES: CONCEPTUAL CHANGE AS REPRESENTATIONAL CHANGE Marion VORMS [email protected] University Paris 1, IHPST (CNRS) 13 rue du Four 75006 Paris, France Abstract The birth of classical genetics in the 1910's was the result of the junction of two modes of analysis, corresponding to two dis- ciplines: Mendelism and cytology. The goal of this paper is to shed some light on the change undergone by the science of he- redity at the time, and to emphasise the subtlety of the concep- tual articulation of Mendelian and cytological hypotheses within classical genetics.
    [Show full text]
  • Genetic Linkage and Crossing Over
    Genetic linkage and Crossing Over Is independent assortment always the case? No • Independent assortment states that during gamete formation, the two alleles for one gene segregate or assort independently of the alleles for other genes. • But if two genes are found on the same chromosome, they will not assort independently, and do not follow Mendelian inheritance patterns. • Genes that are inherited together are said to be “linked.” • Genes located on different chromosomes are not linked This allows independent assortment – in a di-hybrid cross the traits show the classic 9:3:3:1 inheritance pattern. • Genes that are located very close together on the same chromosome may show complete linkage They may be so close to each other that they cannot be separated by recombination during meiosis. (c) Genes located far apart on the same chromosome typically show incomplete (partial) linkage because they are easily separated by recombination. Genetic linkage is the tendency of alleles that are located close together on a chromosome to be inherited together during meiosis. Genes whose loci are nearer to each other are less likely to be separated on to different chromatids during chromosomal crossover, and are therefore said to be genetically linked. In other words, the nearer two genes are on a chromosome, the lower is the chance of a swap occurring between them, and the more likely they are to be inherited together. The discovery of genetic linkage • William Bateson and Reginald Punnett completed a study in 1905 that determined the movement of alleles found on the same chromosome. • The study used sweet peas, particularly flower colour and pollen shape, they followed the inheritance pattern.
    [Show full text]
  • Linkage, Recombination and Eukaryotic Gene Mapping
    2/7/2013 Gene Mapping Physical mapping • Gene mapping involves determining the locations of genes within specific chromosomes. • Two methods of gene mapping are used: • involves determining the exact position of a • genetic mapping • physical mapping specific gene within a chromosome. • • Genetic mapping is used to determine the relative position of There are multiple techniques for genes within a chromosome. This is measured by whether or accomplishing this, including creating cell not two genes are "linked". hybrids for mapping out DNA in specific • If both genes are inherited together they are considered linked. chromosomes. • By determining which genes are linked, the relative positions of genes can be worked out. 1 2 Genetic map • The genes on a chromosome can be represented as a single linear structure that goes from one end of the chromosome to the other. • A genetic map is a representation of the genes on a chromosome arranged in linear order • Also called a linkage map. • Genetic distance is measured by frequency of crossing over Linkage, Recombination and between loci on the same chromosome (distances between loci expressed as percent recombination or (recombination frequency RF) Eukaryotic Gene Mapping – map units (mu), – centimorgans(cM). • One map unit = one centimorgan (cM) = 1% recombination between loci. 3 4 1 2/7/2013 Basic Eukaryotic Chromosome Mapping GENE MAPPING IN EUKARYOTES • Key Concepts • Discovery of genetic linkage 1. Two genes close together on the same chromosome pair do not assort independently at meiosis. 2. Recombination produces genotypes with new combinations of parental • Gene recombination and chromosomal exchange alleles. 3. A pair of homologous chromosomes can exchange segments by crossing- over.
    [Show full text]
  • Linkage and Crossing Over
    Linkage and crossing over Dr. TARUNPREET SINGH LINKAGE CROSSING OVER • Discovery of linkage • Discovery of crossing over • Meaning of linkage • Meaning of crossing over • Characteristics of linkage • Characteristics of crossing • Genes in linkage over • Theories • Types crossing over • Kinds of linkage • Mechanisms • Linkage group • Factors affecting crossing • Significance over • Significance • Differences between crossing over and linkage Discovery of Linkage • The principle of linkage was discovered by English Scientists William Bateson and R.C. Punnet in 1906 in Sweet Pea (Lathyrus odoratus). However, it was put forward as a regular concept by Morgan in 1910 from his work on (Drosophila melanogaster). Meaning of Linkage • Linkage is the phenomenon of AB certain genes staying together during inheritance through AB several generations without any change or separation due to their being present on same chromosomes. CHARACTERISTICS OF LINKAGE • Linkage involves two or more genes which are linked in same chromosomes in a linear fashion. • Linkage reduces variability. • It may involve either dominant or recessive alleles(coupling phase) or some dominant and some recessive alleles(repulsion phase). • It usually involves those genes which are located close to each other. • The strength of linkage depends on the distance between the linked gene. *Lesser the distance higher the strength of linkage* Genes in Linkage • LINKED GENE : These genes do not show independent assortment. It occurs in same chromosome. Dihybrid ratio of linked gene is 3:1 • UNLINKED GENE: These gene show independent assortment. Dihybrid ratio is 9:3:3:1. Theories of Linkage • DIFFERENTIAL MULTIPLICATION THEORY (William Bateson) • CHROMOSOMAL THEORY (Thomas Hunt Morgan) DIFFERENTIAL MULTIPLICATION THEORY • This theory was put forward by Bateson in 1930.
    [Show full text]
  • Linkage, Recombination, and Eukaryotic Gene Mapping 109 Located at the Same Position, Or Locus, on Each of the Two Experiment Homologous Chromosomes
    Linkage, Recombination, and Eukaryotic Gene 5 Mapping Alfred Sturtevant and the First Genetic Map n 1909, Thomas Hunt Morgan taught the introduction to zool- Iogy class at Columbia University. Seated in the lecture hall were sophomore Alfred Henry Sturtevant and freshman Calvin Bridges. Sturtevant and Bridges were excited by Morgan’s teaching style and intrigued by his interest in biological problems. They asked Morgan if they could work in his laboratory and, the following year, both young men were given desks in the “Fly Room,” Morgan’s research laboratory where the study of Drosophila genetics was in its infancy (see pp. 75–76 in Chapter 4). Sturtevant, Bridges, and Morgan’s other research students virtually lived in the laboratory, raising fruit flies, designing experiments, and discussing their results. In the course of their research, Morgan and his students observed that some pairs of genes did not segregate randomly according to Mendel’s principle of independent assortment but instead tended to be inherited together. Morgan suggested that pos- sibly the genes were located on the same chromosome and thus traveled together during meiosis. He further proposed that closely linked genes—those that are rarely shuffled by recombination—lie close together on the same chromosome, whereas loosely linked genes—those more frequently shuffled by recombination—lie far- ther apart. One day in 1911, Sturtevant and Morgan were discussing inde- pendent assortment when, suddenly, Sturtevant had a flash of inspi- ration: variation in the strength of linkage indicated how genes are positioned along a chromosome, providing a way of mapping genes. Sturtevant went home and, neglecting his undergraduate homework, spent most of the night working out the first genetic map (Figure 5.1).
    [Show full text]