Reconstructing Dynamic Microrna Regulated Interaction Networks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![FK506-Binding Protein 12.6/1B, a Negative Regulator of [Ca2+], Rescues Memory and Restores Genomic Regulation in the Hippocampus of Aging Rats](https://docslib.b-cdn.net/cover/6136/fk506-binding-protein-12-6-1b-a-negative-regulator-of-ca2-rescues-memory-and-restores-genomic-regulation-in-the-hippocampus-of-aging-rats-16136.webp)
FK506-Binding Protein 12.6/1B, a Negative Regulator of [Ca2+], Rescues Memory and Restores Genomic Regulation in the Hippocampus of Aging Rats
This Accepted Manuscript has not been copyedited and formatted. The final version may differ from this version. A link to any extended data will be provided when the final version is posted online. Research Articles: Neurobiology of Disease FK506-Binding Protein 12.6/1b, a negative regulator of [Ca2+], rescues memory and restores genomic regulation in the hippocampus of aging rats John C. Gant1, Eric M. Blalock1, Kuey-Chu Chen1, Inga Kadish2, Olivier Thibault1, Nada M. Porter1 and Philip W. Landfield1 1Department of Pharmacology & Nutritional Sciences, University of Kentucky, Lexington, KY 40536 2Department of Cell, Developmental and Integrative Biology, University of Alabama at Birmingham, Birmingham, AL 35294 DOI: 10.1523/JNEUROSCI.2234-17.2017 Received: 7 August 2017 Revised: 10 October 2017 Accepted: 24 November 2017 Published: 18 December 2017 Author contributions: J.C.G. and P.W.L. designed research; J.C.G., E.M.B., K.-c.C., and I.K. performed research; J.C.G., E.M.B., K.-c.C., I.K., and P.W.L. analyzed data; J.C.G., E.M.B., O.T., N.M.P., and P.W.L. wrote the paper. Conflict of Interest: The authors declare no competing financial interests. NIH grants AG004542, AG033649, AG052050, AG037868 and McAlpine Foundation for Neuroscience Research Corresponding author: Philip W. Landfield, [email protected], Department of Pharmacology & Nutritional Sciences, University of Kentucky, 800 Rose Street, UKMC MS 307, Lexington, KY 40536 Cite as: J. Neurosci ; 10.1523/JNEUROSCI.2234-17.2017 Alerts: Sign up at www.jneurosci.org/cgi/alerts to receive customized email alerts when the fully formatted version of this article is published. -

A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated. -
![Downloaded from [266]](https://docslib.b-cdn.net/cover/7352/downloaded-from-266-347352.webp)
Downloaded from [266]
Patterns of DNA methylation on the human X chromosome and use in analyzing X-chromosome inactivation by Allison Marie Cotton B.Sc., The University of Guelph, 2005 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY in The Faculty of Graduate Studies (Medical Genetics) THE UNIVERSITY OF BRITISH COLUMBIA (Vancouver) January 2012 © Allison Marie Cotton, 2012 Abstract The process of X-chromosome inactivation achieves dosage compensation between mammalian males and females. In females one X chromosome is transcriptionally silenced through a variety of epigenetic modifications including DNA methylation. Most X-linked genes are subject to X-chromosome inactivation and only expressed from the active X chromosome. On the inactive X chromosome, the CpG island promoters of genes subject to X-chromosome inactivation are methylated in their promoter regions, while genes which escape from X- chromosome inactivation have unmethylated CpG island promoters on both the active and inactive X chromosomes. The first objective of this thesis was to determine if the DNA methylation of CpG island promoters could be used to accurately predict X chromosome inactivation status. The second objective was to use DNA methylation to predict X-chromosome inactivation status in a variety of tissues. A comparison of blood, muscle, kidney and neural tissues revealed tissue-specific X-chromosome inactivation, in which 12% of genes escaped from X-chromosome inactivation in some, but not all, tissues. X-linked DNA methylation analysis of placental tissues predicted four times higher escape from X-chromosome inactivation than in any other tissue. Despite the hypomethylation of repetitive elements on both the X chromosome and the autosomes, no changes were detected in the frequency or intensity of placental Cot-1 holes. -

Gene Symbol Category ACAN ECM ADAM10 ECM Remodeling-Related ADAM11 ECM Remodeling-Related ADAM12 ECM Remodeling-Related ADAM15 E
Supplementary Material (ESI) for Integrative Biology This journal is (c) The Royal Society of Chemistry 2010 Gene symbol Category ACAN ECM ADAM10 ECM remodeling-related ADAM11 ECM remodeling-related ADAM12 ECM remodeling-related ADAM15 ECM remodeling-related ADAM17 ECM remodeling-related ADAM18 ECM remodeling-related ADAM19 ECM remodeling-related ADAM2 ECM remodeling-related ADAM20 ECM remodeling-related ADAM21 ECM remodeling-related ADAM22 ECM remodeling-related ADAM23 ECM remodeling-related ADAM28 ECM remodeling-related ADAM29 ECM remodeling-related ADAM3 ECM remodeling-related ADAM30 ECM remodeling-related ADAM5 ECM remodeling-related ADAM7 ECM remodeling-related ADAM8 ECM remodeling-related ADAM9 ECM remodeling-related ADAMTS1 ECM remodeling-related ADAMTS10 ECM remodeling-related ADAMTS12 ECM remodeling-related ADAMTS13 ECM remodeling-related ADAMTS14 ECM remodeling-related ADAMTS15 ECM remodeling-related ADAMTS16 ECM remodeling-related ADAMTS17 ECM remodeling-related ADAMTS18 ECM remodeling-related ADAMTS19 ECM remodeling-related ADAMTS2 ECM remodeling-related ADAMTS20 ECM remodeling-related ADAMTS3 ECM remodeling-related ADAMTS4 ECM remodeling-related ADAMTS5 ECM remodeling-related ADAMTS6 ECM remodeling-related ADAMTS7 ECM remodeling-related ADAMTS8 ECM remodeling-related ADAMTS9 ECM remodeling-related ADAMTSL1 ECM remodeling-related ADAMTSL2 ECM remodeling-related ADAMTSL3 ECM remodeling-related ADAMTSL4 ECM remodeling-related ADAMTSL5 ECM remodeling-related AGRIN ECM ALCAM Cell-cell adhesion ANGPT1 Soluble factors and receptors -

Noelia Díaz Blanco
Effects of environmental factors on the gonadal transcriptome of European sea bass (Dicentrarchus labrax), juvenile growth and sex ratios Noelia Díaz Blanco Ph.D. thesis 2014 Submitted in partial fulfillment of the requirements for the Ph.D. degree from the Universitat Pompeu Fabra (UPF). This work has been carried out at the Group of Biology of Reproduction (GBR), at the Department of Renewable Marine Resources of the Institute of Marine Sciences (ICM-CSIC). Thesis supervisor: Dr. Francesc Piferrer Professor d’Investigació Institut de Ciències del Mar (ICM-CSIC) i ii A mis padres A Xavi iii iv Acknowledgements This thesis has been made possible by the support of many people who in one way or another, many times unknowingly, gave me the strength to overcome this "long and winding road". First of all, I would like to thank my supervisor, Dr. Francesc Piferrer, for his patience, guidance and wise advice throughout all this Ph.D. experience. But above all, for the trust he placed on me almost seven years ago when he offered me the opportunity to be part of his team. Thanks also for teaching me how to question always everything, for sharing with me your enthusiasm for science and for giving me the opportunity of learning from you by participating in many projects, collaborations and scientific meetings. I am also thankful to my colleagues (former and present Group of Biology of Reproduction members) for your support and encouragement throughout this journey. To the “exGBRs”, thanks for helping me with my first steps into this world. Working as an undergrad with you Dr. -
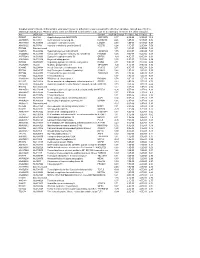
Supplementary File 2A Revised
Supplementary file 2A. Differentially expressed genes in aldosteronomas compared to all other samples, ranked according to statistical significance. Missing values were not allowed in aldosteronomas, but to a maximum of five in the other samples. Acc UGCluster Name Symbol log Fold Change P - Value Adj. P-Value B R99527 Hs.8162 Hypothetical protein MGC39372 MGC39372 2,17 6,3E-09 5,1E-05 10,2 AA398335 Hs.10414 Kelch domain containing 8A KLHDC8A 2,26 1,2E-08 5,1E-05 9,56 AA441933 Hs.519075 Leiomodin 1 (smooth muscle) LMOD1 2,33 1,3E-08 5,1E-05 9,54 AA630120 Hs.78781 Vascular endothelial growth factor B VEGFB 1,24 1,1E-07 2,9E-04 7,59 R07846 Data not found 3,71 1,2E-07 2,9E-04 7,49 W92795 Hs.434386 Hypothetical protein LOC201229 LOC201229 1,55 2,0E-07 4,0E-04 7,03 AA454564 Hs.323396 Family with sequence similarity 54, member B FAM54B 1,25 3,0E-07 5,2E-04 6,65 AA775249 Hs.513633 G protein-coupled receptor 56 GPR56 -1,63 4,3E-07 6,4E-04 6,33 AA012822 Hs.713814 Oxysterol bining protein OSBP 1,35 5,3E-07 7,1E-04 6,14 R45592 Hs.655271 Regulating synaptic membrane exocytosis 2 RIMS2 2,51 5,9E-07 7,1E-04 6,04 AA282936 Hs.240 M-phase phosphoprotein 1 MPHOSPH -1,40 8,1E-07 8,9E-04 5,74 N34945 Hs.234898 Acetyl-Coenzyme A carboxylase beta ACACB 0,87 9,7E-07 9,8E-04 5,58 R07322 Hs.464137 Acyl-Coenzyme A oxidase 1, palmitoyl ACOX1 0,82 1,3E-06 1,2E-03 5,35 R77144 Hs.488835 Transmembrane protein 120A TMEM120A 1,55 1,7E-06 1,4E-03 5,07 H68542 Hs.420009 Transcribed locus 1,07 1,7E-06 1,4E-03 5,06 AA410184 Hs.696454 PBX/knotted 1 homeobox 2 PKNOX2 1,78 2,0E-06 -

Anti-SERPINA9 / GCET1 Antibody (ARG41824)
Product datasheet [email protected] ARG41824 Package: 100 μl anti-SERPINA9 / GCET1 antibody Store at: -20°C Summary Product Description Rabbit Polyclonal antibody recognizes SERPINA9 / GCET1 Tested Reactivity Hu, Ms, Rat Tested Application WB Host Rabbit Clonality Polyclonal Isotype IgG Target Name SERPINA9 / GCET1 Antigen Species Human Immunogen Synthetic peptide of Human SERPINA9 / GCET1. Conjugation Un-conjugated Alternate Names SERPINA11; Centerin; Germinal center B-cell-expressed transcript 1 protein; SERPINA11b; GCET1; Serpin A9 Application Instructions Application table Application Dilution WB 1:500 - 1:2000 Application Note * The dilutions indicate recommended starting dilutions and the optimal dilutions or concentrations should be determined by the scientist. Positive Control MCF7 Calculated Mw 47 kDa Observed Size ~ 48 kDa Properties Form Liquid Purification Affinity purified. Buffer PBS (pH 7.4), 150 mM NaCl, 0.02% Sodium azide and 50% Glycerol. Preservative 0.02% Sodium azide Stabilizer 50% Glycerol Storage instruction For continuous use, store undiluted antibody at 2-8°C for up to a week. For long-term storage, aliquot and store at -20°C. Storage in frost free freezers is not recommended. Avoid repeated freeze/thaw cycles. Suggest spin the vial prior to opening. The antibody solution should be gently mixed before use. Note For laboratory research only, not for drug, diagnostic or other use. www.arigobio.com 1/2 Bioinformation Gene Symbol SERPINA9 Gene Full Name serpin peptidase inhibitor, clade A (alpha-1 antiproteinase, antitrypsin), member 9 Function Protease inhibitor that inhibits trypsin and trypsin-like serine proteases (in vitro). Inhibits plasmin and thrombin with lower efficiency (in vitro). [UniProt] Cellular Localization Isoform 1: Secreted. -

Haploinsufficiency of Cardiac Myosin Binding Protein-C in the Development of Hypertrophic Cardiomyopathy
Loyola University Chicago Loyola eCommons Dissertations Theses and Dissertations 2014 Haploinsufficiency of Cardiac Myosin Binding Protein-C in the Development of Hypertrophic Cardiomyopathy David Barefield Loyola University Chicago Follow this and additional works at: https://ecommons.luc.edu/luc_diss Part of the Physiology Commons Recommended Citation Barefield, David, "Haploinsufficiency of Cardiac Myosin Binding Protein-C in the Development of Hypertrophic Cardiomyopathy" (2014). Dissertations. 1249. https://ecommons.luc.edu/luc_diss/1249 This Dissertation is brought to you for free and open access by the Theses and Dissertations at Loyola eCommons. It has been accepted for inclusion in Dissertations by an authorized administrator of Loyola eCommons. For more information, please contact [email protected]. This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 License. Copyright © 2014 David Barefield LOYOLA UNIVERSITY CHICAGO HAPLOINSUFFICIENCY OF CARDIAC MYOSIN BINDING PROTEIN-C IN THE DEVELOPMENT OF HYPERTROPHIC CARDIOMYOPATHY A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY PROGRAM IN CELL AND MOLECULAR PHYSIOLOGY BY DAVID YEOMANS BAREFIELD CHICAGO, IL AUGUST 2014 Copyright by David Yeomans Barefield, 2014 All Rights Reserved. ii ACKNOWLEDGEMENTS The completion of this work would not have been possible without the support of excellent mentors, colleagues, friends, and family. I give tremendous thanks to my mentor, Dr. Sakthivel Sadayappan, who has facilitated my growth as a scientist and as a human being over the past five years. I would like to thank my dissertation committee: Drs. Pieter de Tombe, Kenneth Byron, Leanne Cribbs, Kyle Henderson, and Christine Seidman for their erudite guidance of my project and my development as a scientist. -

Lineage-Specific Programming Target Genes Defines Potential for Th1 Temporal Induction Pattern of STAT4
Downloaded from http://www.jimmunol.org/ by guest on October 1, 2021 is online at: average * The Journal of Immunology published online 26 August 2009 from submission to initial decision 4 weeks from acceptance to publication J Immunol http://www.jimmunol.org/content/early/2009/08/26/jimmuno l.0901411 Temporal Induction Pattern of STAT4 Target Genes Defines Potential for Th1 Lineage-Specific Programming Seth R. Good, Vivian T. Thieu, Anubhav N. Mathur, Qing Yu, Gretta L. Stritesky, Norman Yeh, John T. O'Malley, Narayanan B. Perumal and Mark H. Kaplan Submit online. Every submission reviewed by practicing scientists ? is published twice each month by http://jimmunol.org/subscription Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts http://www.jimmunol.org/content/suppl/2009/08/26/jimmunol.090141 1.DC1 Information about subscribing to The JI No Triage! Fast Publication! Rapid Reviews! 30 days* • Why • • Material Permissions Email Alerts Subscription Supplementary The Journal of Immunology The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2009 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. This information is current as of October 1, 2021. Published August 26, 2009, doi:10.4049/jimmunol.0901411 The Journal of Immunology Temporal Induction Pattern of STAT4 Target Genes Defines Potential for Th1 Lineage-Specific Programming1 Seth R. Good,2* Vivian T. Thieu,2† Anubhav N. Mathur,† Qing Yu,† Gretta L. -

Analysis and Interpretation of Next-Generation Sequencing Data for the Identification of Genetic Variants Involved in Cardiovascular Malformation
Analysis and interpretation of next-generation sequencing data for the identification of genetic variants involved in cardiovascular malformation Darren T. Houniet For the degree of Doctor of Philosophy Newcastle University Faculty of Medical Sciences Institute of Genetic Medicine February 2013 Abstract Congenital cardiovascular malformation (CVM) affects 7/1000 live births. Approximately 20% of cases are caused by chromosomal and syndromic conditions. Rare Mendelian families segregating particular forms of CVM have also been described. Among the remaining 80% of non-syndromic cases, there is a familial predisposition implicating as yet unidentified genetic factors. Since the reproductive consequences to an individual of CVM are usually severe, evolutionary considerations suggest predisposing variants are likely to be rare. The overall aim of my PhD was to use next generation sequencing (NGS) methods to identify such rare, potentially disease causing variants in CVM. First, I developed a novel approach to calculate the sensitivity and specificity of NGS data in detecting variants using publicly available population frequency data. My aim was to provide a method that would yield sound estimates of the quality of a sequencing experiment without the need for additional genotyping in the sequenced samples. I developed such a method and demonstrated that it provided comparable results to methods using microarray data as a reference. Furthermore, I evaluated different variant calling pipelines and showed that they have a large effect on sensitivity and specificity. Following this, the NovoAlign-Samtools and BWA-Dindel pipelines were used to identify single base substitution and indel variants in three pedigrees, where predisposition to a different disease appears to segregate following an autosomal dominant mode of inheritance. -

The Correlation of Keratin Expression with In-Vitro Epithelial Cell Line Differentiation
The correlation of keratin expression with in-vitro epithelial cell line differentiation Deeqo Aden Thesis submitted to the University of London for Degree of Master of Philosophy (MPhil) Supervisors: Professor Ian. C. Mackenzie Professor Farida Fortune Centre for Clinical and Diagnostic Oral Science Barts and The London School of Medicine and Dentistry Queen Mary, University of London 2009 Contents Content pages ……………………………………………………………………......2 Abstract………………………………………………………………………….........6 Acknowledgements and Declaration……………………………………………...…7 List of Figures…………………………………………………………………………8 List of Tables………………………………………………………………………...12 Abbreviations….………………………………………………………………..…...14 Chapter 1: Literature review 16 1.1 Structure and function of the Oral Mucosa……………..…………….…..............17 1.2 Maintenance of the oral cavity...……………………………………….................20 1.2.1 Environmental Factors which damage the Oral Mucosa………. ….…………..21 1.3 Structure and function of the Oral Mucosa ………………...….……….………...21 1.3.1 Skin Barrier Formation………………………………………………….……...22 1.4 Comparison of Oral Mucosa and Skin…………………………………….……...24 1.5 Developmental and Experimental Models used in Oral mucosa and Skin...……..28 1.6 Keratinocytes…………………………………………………….….....................29 1.6.1 Desmosomes…………………………………………….…...............................29 1.6.2 Hemidesmosomes……………………………………….…...............................30 1.6.3 Tight Junctions………………………….……………….…...............................32 1.6.4 Gap Junctions………………………….……………….….................................32 -
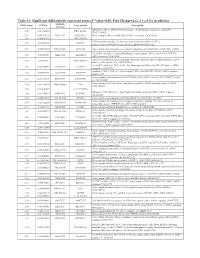
(P -Value<0.05, Fold Change≥1.4), 4 Vs. 0 Gy Irradiation
Table S1: Significant differentially expressed genes (P -Value<0.05, Fold Change≥1.4), 4 vs. 0 Gy irradiation Genbank Fold Change P -Value Gene Symbol Description Accession Q9F8M7_CARHY (Q9F8M7) DTDP-glucose 4,6-dehydratase (Fragment), partial (9%) 6.70 0.017399678 THC2699065 [THC2719287] 5.53 0.003379195 BC013657 BC013657 Homo sapiens cDNA clone IMAGE:4152983, partial cds. [BC013657] 5.10 0.024641735 THC2750781 Ciliary dynein heavy chain 5 (Axonemal beta dynein heavy chain 5) (HL1). 4.07 0.04353262 DNAH5 [Source:Uniprot/SWISSPROT;Acc:Q8TE73] [ENST00000382416] 3.81 0.002855909 NM_145263 SPATA18 Homo sapiens spermatogenesis associated 18 homolog (rat) (SPATA18), mRNA [NM_145263] AA418814 zw01a02.s1 Soares_NhHMPu_S1 Homo sapiens cDNA clone IMAGE:767978 3', 3.69 0.03203913 AA418814 AA418814 mRNA sequence [AA418814] AL356953 leucine-rich repeat-containing G protein-coupled receptor 6 {Homo sapiens} (exp=0; 3.63 0.0277936 THC2705989 wgp=1; cg=0), partial (4%) [THC2752981] AA484677 ne64a07.s1 NCI_CGAP_Alv1 Homo sapiens cDNA clone IMAGE:909012, mRNA 3.63 0.027098073 AA484677 AA484677 sequence [AA484677] oe06h09.s1 NCI_CGAP_Ov2 Homo sapiens cDNA clone IMAGE:1385153, mRNA sequence 3.48 0.04468495 AA837799 AA837799 [AA837799] Homo sapiens hypothetical protein LOC340109, mRNA (cDNA clone IMAGE:5578073), partial 3.27 0.031178378 BC039509 LOC643401 cds. [BC039509] Homo sapiens Fas (TNF receptor superfamily, member 6) (FAS), transcript variant 1, mRNA 3.24 0.022156298 NM_000043 FAS [NM_000043] 3.20 0.021043295 A_32_P125056 BF803942 CM2-CI0135-021100-477-g08 CI0135 Homo sapiens cDNA, mRNA sequence 3.04 0.043389246 BF803942 BF803942 [BF803942] 3.03 0.002430239 NM_015920 RPS27L Homo sapiens ribosomal protein S27-like (RPS27L), mRNA [NM_015920] Homo sapiens tumor necrosis factor receptor superfamily, member 10c, decoy without an 2.98 0.021202829 NM_003841 TNFRSF10C intracellular domain (TNFRSF10C), mRNA [NM_003841] 2.97 0.03243901 AB002384 C6orf32 Homo sapiens mRNA for KIAA0386 gene, partial cds.