Procedure for Noise Mapping Updating in Urban Area
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Itinerari Di Architettura Milanese
ORDINE DEGLI ARCHITETTI, FONDAZIONE DELL’ORDINE DEGLI ARCHITETTI, PIANIFICATORI, PAESAGGISTI E CONSERVATORI PIANIFICATORI, PAESAGGISTI E CONSERVATORI DELLA PROVINCIA DI MILANO DELLA PROVINCIA DI MILANO /figure ritratti dal professionismo milanese Piero Bottoni: la dimensione civile della bellezza Giancarlo Consonni Graziella Tonon Itinerari di architettura milanese L’architettura moderna come descrizione della città “Itinerari di architettura milanese: l’architettura moderna come descrizione della città” è un progetto dell’Ordine degli Architetti P.P.C. della Provincia di Milano a cura della sua Fondazione. Coordinamento scientifico: Maurizio Carones Consigliere delegato: Paolo Brambilla Responsabili della redazione: Alessandro Sartori, Stefano Suriano Coordinamento attività: Giulia Pellegrino Ufficio Stampa: Ferdinando Crespi “Piero Bottoni: la dimensione civile della bellezza” Giancarlo Consonni, Graziella Tonon a cura di: Alessandro Sartori, Stefano Suriano, Barbara Palazzi Per le immagini si ringrazia: Archivio Piero Bottoni in quarta di copertina: Piero Bottoni, Schizzo di studio per il Padiglione mostre al QT8, 1951 La Fondazione dell’Ordine degli Architetti P.P.C. della Provincia di Milano rimane a disposizione per eventuali diritti sui materiali iconografici non identificati www.ordinearchitetti.mi.it www.fondazione.ordinearchitetti.mi.it Piero Bottoni: la dimensione civile della bellezza Nei quarant’anni centrali del XX secolo la vicenda di Piero Bottoni si intreccia con la storia di Milano. Chi si occupi delle trasformazioni -
Welcome to Milan
WELCOME TO MILAN WHAT MILAN IS ALL ABOUT MEGLIOMILANO MEGLIOMILANO The brochure WELCOME TO MILAN marks the attention paid to those who come to Milan either for business or for study. A fi rst welcome approach which helps to improve the image of the city perceived from outside and to describe the city in all its various aspects. The brochure takes the visitor to the historical, cultural and artistic heritage of the city and indicates the services and opportunities off ered in a vivid and dynamic context as is the case of Milan. MeglioMilano, which is deeply involved in the “hosting fi eld” as from its birth in 1987, off ers this brochure to the city and its visitors thanks to the attention and the contribution of important Institutions at a local level, but not only: Edison SpA, Expo CTS and Politecnico of Milan. The cooperation between the public and private sectors underlines the fact that the city is ever more aiming at off ering better and useable services in order to improve the quality of life in the city for its inhabitants and visitors. Wishing that WELCOME TO MILAN may be a good travel companion during your stay in Milan, I thank all the readers. Marco Bono Chairman This brochure has been prepared by MeglioMilano, a non-profi t- making association set up by Automobile Club Milan, Chamber of Commerce and the Union of Commerce, along with the Universities Bocconi, Cattolica, Politecnico, Statale, the scope being to improve the quality of life in the city. Milan Bicocca University, IULM University and companies of diff erent sectors have subsequently joined. -

Milan Dynamic Noise Mapping from Few Monitoring Stations: Statistical Analysis on Road Network
INTER-NOISE 2016 Milan dynamic noise mapping from few monitoring stations: statistical analysis on road network Giovanni ZAMBON1; Roberto BENOCCI2; Alessandro BISCEGLIE3; H. Eduardo ROMAN4 1-2-3 Dipartimento di Scienze dell’Ambiente e del Territorio e di Scienze della Terra, University of Milano - Bicocca, Italy 4 Dipartimento di Fisica “G. Occhialini”, Università degli Studi di Milano–Bicocca, Milan, Italy ABSTRACT One of the main objectives of "Dynamap" project is to realize a dynamic noise map within a given area of the city of Milan, containing about 2000 road arches, by using approximately 20 continuous measuring stations. This map is scheduled to be updated dynamically within a period of time varying from 5 minutes to 1 hour. The ability to obtain reliable maps within a complex urban context is linked to the fact that the vehicle flow patterns are very regular. In the first phase of the project, we monitored nearly 100 roads for a period of at least 24 hours. Then, these roads have been aggregated by means of a cluster analysis, depending on their noise level profiles. The analysis of the distribution of a non-acoustical parameter in the clusters, such as the vehicular flow rate, allowed to attribute a specific noise profile to a road not present in the database. It was also possible to select the most representative arches, among the 2000 arches to be mapped, where the monitoring stations will be installed. It was finally estimated the error associated with the noise levels of the dynamic maps as a function of the updating time interval. -

For an Urban History of Milan, Italy: the Role Of
FOR AN URBAN HISTORY OF MILAN, ITALY: THE ROLE OF GISCIENCE DISSERTATION Presented to the Graduate Council of Texas State University‐San Marcos in Partial Fulfillment of the Requirements for the Degree Doctor of PHILOSOPHY by Michele Tucci, B.S., M.S. San Marcos, Texas May 2011 FOR AN URBAN HISTORY OF MILAN, ITALY: THE ROLE OF GISCIENCE Committee Members Approved: ________________________________ Alberto Giordano ________________________________ Sven Fuhrmann ________________________________ Yongmei Lu ________________________________ Rocco W. Ronza Approved: ______________________________________ J. Micheal Willoughby Dean of the Gradute Collage COPYRIGHT by Michele Tucci 2011 ACKNOWLEDGEMENTS My sincere thanks go to all those people who spent their time and effort to help me complete my studies. My dissertation committee at Texas State University‐San Marcos: Dr. Yongmei Lu who, as a professor first and as a researcher in a project we worked together then, improved and stimulated my knowledge and understanding of quantitative analysis; Dr. Sven Fuhrmann who, in many occasions, transmitted me his passion about cartography, computer cartography and geovisualization; Dr. Rocco W. Ronza who provided keen insight into my topic and valuable suggestions about historical literature; and especially Dr. Alberto Giordano, my dissertation advisor, who, with patience and determination, walked me through this process and taught me the real essence of conducting scientific research. Additional thanks are extended to several members of the stuff at the Geography Department at Texas State University‐San Marcos: Allison Glass‐Smith, Angelika Wahl and Pat Hell‐Jones whose precious suggestions and help in solving bureaucratic issues was fundamental to complete the program. My office mates Matthew Connolly and Christi Townsend for their cathartic function in listening and sharing both good thought and sometimes frustrations of being a doctoral student. -

Open Streets
Milan 2020. Adaptation strategy Open Streets 1 Table of contents: Adapting the city to social distancing measures 3 An unprecedented opportunity International examples Solutions already experimented in Milan Strategies for an active mobility 10 Cycling as a key factor towards a sustainable mobility Walking at the heart of urban life Empowering public space around neighborhoods Trial cases and experimentations 19 Interventions involving signage only Interventions involving parking-protected signage Interventions involving signage and emergency devices Two-way cycling lanes Traffic control interventions Shared streets Sidewalk expansion Pedestrian-only streets Parklet Other experiments Scheduled actions and interventions 24 Planned actions Scheduled interventions Implementation examples 2 Adapting the city to social distancing measures The pandemic changed our habits, challenged our lifestyles, disrupted our daily priorities and limited freedoms that seemed unquestionable. Among the things we are missing the most in our cities during the lockdown, one in particular remains a universal essential need: moving around. Although not immediate, the gradual reopening of the city is getting closer and closer. We will soon be able to move around again and integrate physical activity into our daily routines. Thus, it is more and more urgent to find solutions to adapt the city - particularly infrastructure and public spaces - to the new social distancing measures needed to coexist with the virus. This is a seemingly obvious, but unprecedented issue. Compliance with such measures will not be easy, especially when it comes to managing people's movements in densely populated cities like Milan. But in the coming months, mobility will have to change in an effort to find a new balance that manages the movements of people and ensures their protection from the risk of infection. -
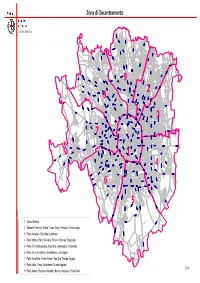
Impagin 9 Zone
Zone di Decentramento Settore Statistica V i a C o m a s i n a V ia V l i e a R u G b . ic o P n a e s t a i t s e T . F e l a i V ani V gn i odi a ta M . Lit L A . Via V ia O l r e n E a . t F o e r V m i a i A s t e s a a n z i n orett i Am o Via C. M e l a i V V V i i a V a i B a M G o . v . L i B s . e a a G s s r s c d a o e s a r n s B i a . F ia V i t s e T V . V F i a a v i ado a l e P l ia e V P a i e E l . V l e F g e r r i n m o i V ia R o M s am s b i r et ti Piazza dell'Ospedale Maggiore a a v z o n n a o lm M a P e l ia a i V V a v Via V o G i d all a a ara ni P te B ia a o nd i a V v . C i G s ia V a V ia s A c a p a e l p i e C n n a in i i V V ia G al V V lar i i at ia hini a e V mbrusc Piazza h V i Via La C c V a r i a C Bausan . -

Monitoring and Prediction of Traffic Noise in Large Urban Areas
applied sciences Review Monitoring and Prediction of Traffic Noise in Large Urban Areas Giovanni Zambon 1, Hector Eduardo Roman 2, Maura Smiraglia 1 and Roberto Benocci 1,* 1 Department of Earth and Environmental Sciences (DISAT), University of Milano-Bicocca, Piazza della Scienza 1, 20126 Milano, Italy; [email protected] (G.Z.); [email protected] (M.S.) 2 Department of Physics, University of Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy; [email protected] * Correspondence: [email protected]; Tel.: +39-02-6448-2108 Received: 1 December 2017; Accepted: 30 January 2018; Published: 7 February 2018 Featured Application: The method discussed in this paper has applications in the context of predicting traffic noise in large urban environments. The system designed by the authors provides an accurate description of traffic noise by relying on measurements of road noise from few monitoring stations appropriately distributed over the zone of interest. A prescription is given of how to choose the location of the noise stations. Abstract: Dynamap, a co-financed project by the European Commission through the Life+ 2013 program, aims at developing a dynamic approach for noise mapping that is capable of updating environmental noise levels through a direct link with a limited number of noise monitoring terminals. Dynamap is based on the idea of finding a suitable set of roads that display similar traffic noise behavior (temporal noise profile over an entire day) so that one can group them together into a single noise map. Each map thus represents a group of road stretches whose traffic noise will be updated periodically, typically every five minutes during daily hours and every hour during night. -

Nota Al Lavoro Di Gap Analysis GRI G3
Sustainability Report 2013 – Pirelli & C. S.p.A. 1 VOLUME 3 of Annual Financial Report at December 31, 2013 Sustainability Report 2013 – Pirelli & C. S.p.A. SUSTAINABILITY REPORT 2013 VOLUME 3 of ANNUAL FINANCIAL REPORT AT DECEMBER 31, 2013 Pirelli & C. S.p.A. – Milan 2 VOLUME 3 of Annual Financial Report at December 31, 2013 Sustainability Report 2013 – Pirelli & C. S.p.A. CONTENTS A Note on Methodology Chapter 1: Creation of Sustainable Value Chapter 2: Economic Dimension Chapter 3: Environmental Dimension Chapter 4: Social Dimension Summary Tables Assurance Statement 3 VOLUME 3 of Annual Financial Report at December 31, 2013 Sustainability Report 2013 – Pirelli & C. S.p.A. A NOTE ON METHODOLOGY The Pirelli Group Sustainability Report, in 2013 at the ninth edition, is the expression of a corporate culture based on the integration of economic, environmental and social choices, in line with the triple bottom line approach. For this reason, instead of being published separately, the description of Pirelli sustainable performance is included as an integral part of the Pirelli Annual Financial Report at December 31, 2013, of which it is the third volume: Volume 1: Annual Financial Report at December 31, 2013; Volume 2: Annual Report on Corporate Governance and the Structure of Share Ownership 2013; Volume 3: Sustainability Report 2013. In light of this integration, note that: the Chairman’s Letter at the beginning of Volume 1 of the Pirelli Annual Financial Report addresses Group sustainability issues; the scope and reporting period of this annual report is the same as the Group’s Annual Financial Report at December 31, 2013 – Volume 1; this report gives a summary of the corporate identity, Group structure and operating performance in 2013, insofar as these topics are discussed in detail in Volume 1, to which reference is made for further information; the Summary Tables, found at the end of the report, link the specific GRI-G4 indicators with the principles of the Global Compact and the topics discussed both in this Volume and in Volumes 1 and 2. -

Sustainability Report 2019 Coima Sustainability Report 2019
SUSTAINABILITY REPORT 2019 COIMA SUSTAINABILITY REPORT 2019 VeniceII - Hotel Excelsior - Internal courtyard SUSTAINABILITY REPORT 2019 COIMA Eva Fumagalli Giovanni Palmenta Luciano Gabriel Rita Palumbo COIMA achieved its Giancluca Galeota Alessandro Panzeri objectives 2019 Alessandra Galvani Luca Parenti in thanks to: Giorgio Garioni Victor Pasecnikov Salvatore Garofalo Marcello Passoni Lucia Garutti Marina Pazzona Mariagrazia Acconciamessa Kelly Catella Russell Elena Gauriso Sara Peccenini Giacomo Aguzzi Alessandra Cauvin Marco Gazze’ Giorgio Pedretti Milena Alberti Romina Cavioni Franco Gerbino Luca Penati Alessandra Alfei Antonella Centra Michele Germano Genesis Perez Feras Abdulaziz Al-Naama Roberto Chissalè Alessandro Ghilotti Pietro Perrone Alessandra Alzetta Paolo Ermenegildo Ciocca Alberto Goretti Chiara Peruzzotti Francesco Antognoni Pieri Ciravolo Deborah Grassi Mattia Peverelli Antonino Aragona Carlotta Ciuffardi Salvatore Grasso Cristiana Pislor Hughes Lorenzo Arcadia Alessia Clerici Enrico Grillo Martina Pislor Agostino Ardissone Samuel Cocci Giulia Grisendi Ruggero Poma Chiara Aver Mirko Colombi Tommaso Gualdi Simona Pozzoli Andrea Baccuini Carlotta Colombo Elena Guariso Marco Puddu Ezechia Baldassari Francesca Colombo Nicol Havè Matteo Ravà Dario Baltuzzi Francesca Colombo Valentina Iacopino Matteo Renzulli Ludovico Barassi Gloria Colombo Danilo Indrio Stefano Rigoni Lorenzo Barbato Marco Comes Lorenzo Infrano Cristiano Rossetto Carlotta Barbieri Nicolò Comparoto Gabriella Iozzino Cristina Rossi Valerio Barbirato Roberta -

Brochure Uptown New.Pdf
Finance Partner Benvenuto ad UpTown Il distretto più green e più smart d’Italia Edizione Marzo 2020 4 SMART CITY | OBIETTIVO SMART CITY 5 Sezione Titolo Indice SOSTENIBILITÀ A 360° 20 IL PARCO PUBBLICO 24 08 UNA NUOVA CENTRALITÀ METROPOLITANA MOBILITÀ SOSTENIBILE 26 10 UNA POSIZIONE STRATEGICA, CONNESSA CON IL MONDO CENTRO COMMERCIALE 28 12 MIND - UPTOWN, NUOVO POLO DI INNOVAZIONE DISTRETTO DELL’ISTRUZIONE 30 14 DA SMART CITY A WELLBEING CITY LA CASCINA, CUORE DELLA COMUNITÀ DEL DISTRETTO 32 16 PARTNER DI ECCELLENZA L’ECOSISTEMA DI SERVIZI 34 18 MASTERPLAN UPTOWN, IL CUORE RESIDENZIALE 36 8 UPTOWN | IL DISTRETTO PIÙ GREEN E PIÙ SMART D’ITALIA UNA NUOVA CENTRALITÀ METROPOLITANA 9 Prodotto interno lordo (Pil) pro capite, in standard di potere d’acquisto (PPS), in rapporto alla media UE-28, per regioni NUTS 2, 2015 (% della media UE-28, UE-28 = 100) Una nuova Fonte: Eurostat (nama_10r_2gdp) e (nama_10_pc) centralità metropolitana Fiera Milano è un logo registrato da Fiera Milano spa MIND è un logo registrato da Arexpo spa UpTown è un logo registrato da Euromilano spa La crescita è una condizione naturale. conseguente incremento della popolazione studentesca. Settori >= 150 125 - < 150 Milano è crescita. È la città italiana più quali la Farmaceutica, del design, della moda, della salute e 100 - < 125 90 - < 100 proiettata verso il futuro, l’unica che possa della biomedica, della finanza, della cultura con eventi di portata 75 - < 90 <75 aspirare al ruolo di global city internazionale, nazionale e internazionale ormai con cadenza settimanale, Sanità • all’interno delle nascenti reti di città. Milano attraggono e continueranno ad attrarre residenti, city users e Ricerca • ha fatto questa scelta di visione strategica, urban travellers negli anni a venire. -

A 3D Geodatabase for Urban Underground Infrastructures: Implementation and Application to Groundwater Management in Milan Metropolitan Area
International Journal of Geo-Information Article A 3D Geodatabase for Urban Underground Infrastructures: Implementation and Application to Groundwater Management in Milan Metropolitan Area Davide Sartirana * , Marco Rotiroti , Chiara Zanotti , Tullia Bonomi , Letizia Fumagalli and Mattia De Amicis Department of Earth and Environmental Sciences, University of Milano-Bicocca, Piazza Della Scienza 1, 20126 Milan, Italy; [email protected] (M.R.); [email protected] (C.Z.); [email protected] (T.B.); [email protected] (L.F.); [email protected] (M.D.A.) * Correspondence: [email protected]; Tel.: +39-02-6448-2882 Received: 16 September 2020; Accepted: 19 October 2020; Published: 21 October 2020 Abstract: The recent rapid increase in urbanization has led to the inclusion of underground spaces in urban planning policies. Among the main subsurface resources, a strong interaction between underground infrastructures and groundwater has emerged in many urban areas in the last few decades. Thus, listing the underground infrastructures is necessary to structure an urban conceptual model for groundwater management needs. Starting from a municipal cartography (Open Data), thus making the procedure replicable, a GIS methodology was proposed to gather all the underground infrastructures into an updatable 3D geodatabase (GDB) for the metropolitan city of Milan (Northern Italy). The underground volumes occupied by three categories of infrastructures were included in the GDB: (a) private car parks, (b) public car parks and (c) subway lines and stations. The application of the GDB allowed estimating the volumes lying below groundwater table in four periods, detected as groundwater minimums or maximums from the piezometric trend reconstructions. -

CITYLIFE the BIRTH of MODERN SCULPTURE Focus on Smart Living Solutions, Wellness and Personal Care
2 JANUARY GUIDE DOWNTOWN 米兰小程序 扫码使用体验 CERITH WYN EVANS “…THE ILLUMINATING GAS” 3 EXHIBITIONS The display by the Scottish artist focuses on the use of language EVENTS 米兰旅行免费指南 and on its perception, which is analysed by sculptures, installations, movies and pictures. Neon installations play a key role in the artist’s production, reflecting the expressive potential of sound and light. A starred gala Conceived by La Scala étoile › 31 October 2019 – 23 February 2020 Roberto Bolle, the event, divided Pirelli HangarBicocca, via Chiese 2 into four gala evenings, celebrates pirellihangarbicocca.org dance in all its multi-faceted forms, with a succession of classic ANTONIO CANOVA. IDEAL HEADS and contemporary ballets that Map Town of Out Spread over 5 sections, the display features a selection of female reach their climax in the four MILANO SKYLINE busts of mythological characters, personalities from the world of performances of the eagerly- Map Subway literature and personified concepts where the artist studies the awaited performance titled Map Shopping different variations of the ideal classical beauty. Roberto Bolle & Friends. › CONTAINS 25 October 2019 – 15 March 2020 › GALA ROBERTO BOLLE GAM Milano, via Palestro 16. & FRIENDS www.gam-milano.com 4 – 7 January 2020 FRIENDS Teatro degli Arcimboldi, ARTEMISIA GENTILESCHI. viale dell’Innovazione 20 & BOLLE Ph © Flavio Lo Scalzo ADORATION OF THE THREE WISE MEN teatroarcimboldi.it Milan’s Museo Diocesano hosts the precious altarpiece by baroque www.robertobolle.com ROBERTO painter Artemia Gentileschi. The work, a loan from Diocesi di Pozzuoli Romano Luciano © Ph The masters of modern sculpture near Naples, reflects the spirit and the themes of the festive season.