DOCSLIB.ORG

A History of the Teaching of Elementary Geometry, with Reference to Present

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A History of the Teaching of Elementary Geometry, with Reference to Present 'j'^iAn^-A^ s-^*ru<<<,.<Lfi.<u'fct,.*—. \A<\,^Ji^...,.. l\:.-^.t^.^-)..-^. 3.l.,...I.La... 3 1924 055 723 203 The original of this bool< is in the Cornell University Library. There are no known copyright restrictions in the United States on the use of the text. http://www.archive.org/details/cu31924055723203 Columbia IHniversit^ (Tontributione to lEbucation tCeacbers College Seriea no. 23 A History of the Teaching of Elementary Geometry Alva Walker Stamper, A. M. Submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy, in the Faculty of Philosophy, Columbia University. NEW YORK 1909 PREFACE While much has been written on the history of mathematics, comparatively little attention has been given to the history of its teaching. Gunther's " Geschichte des mathematischen Unter- richts im Deutschen Mittelalter bis zum Jahre 1525" and Suter's "Die Mathematik auf den Universitaten des Mittelalters " are the only prominent works that emphasize the teaching side. Among the works that treat the general history of mathematics, those of Cantor, Hankel, Gow, and Allman have been of great assistance. Much information has also been gained from miscellaneous articles, standard works on the history of educa- tion, and early texts, the latter constituting, for the most part, the original sources for this study. The material that has been utilized in the first three chapters is to be found chiefly in the standard histories of mathematics, but wherever possible the original sources have been consulted. Originality is claimed only for the selection and arrangement of this portion of the subject-matter and for the conclusions drawn. The material for the next three chapters has been gleaned very largely from the original sources. The author is under great obligation to Professor David Eugene Smith of Teachers College, Columbia University, under whose direction this dissertation has been prepared, for helpful counsel and criticism, and for rendering much of this work possible through his valuable collection of early printed books. Alva Wai.ke;r Stamper. New York, June, 1906. CONTENTS CHAPTER I PAGS THE TEACHING OF GEOMETRY BEFORE EUCLID Thb Beginning of Gbombtry Among Primitive People . 1-4 Intuitive stage 2-3 Stage in which principles are recognized. Ability to classify. Formation of rules. Practical use .... 3-4 Logical stage 4 Application with logic as a basis 4 The Egyptians 4-10 Influences that helped to develop their geometry .... 4-7 The pyramids. Rope Stretchers. Astronomy .^thetic influence. Mural decorations Utilitarian influence. The overflow of the Nile Records. —The manuscript of Ahmes; inscriptions on the Temple at Edfu 7-9 Summary 9—10 The Greeks before Euclid 10-26 The development oj the subject-matter of elementary geometry . 10-16 Thales and his school 10-11 The first propositions given to geometry. The practical not neglected. First problems of construction. Development of a deductive geometry of lines Pythagoras and his school 11-13 Development of the geometry of areas. Further contributions. Nothing known of methods of proof. Geometry becomes an abstract science The development of geometry at Athens .... 13-16 Interest in geometry. The Sophists. The schools of Plato and Aristotle. The Three Problems of Antiquity and their relation to the development of the subject-matter of geometry .... 13 Books written on geometry. Euclid not the first. Nature of the contributions. The "Eudemian Summary." The founding of solid geometry by Eudoxus 13-16 Lack of harmony between the historic sequence and that given later by Euclid 16 Educational features of the Greek geometry 16-26 In the Ionian and Pythagorean schools .... 16-17 At Athens 17-25 The Socratic method. The old Greek education. Plato's disposition of geometry in the curriculum 17-18 Four-fold division of the mathematical sciences . 18-19 Restriction as to the use of instruments . 19-20 V vi Contents Neglect of the study of solid geometry 20 Lettering of figures 21 Drawing of figures 21 Tendency to hold to the special 21-22 Conciseness of proofs . 22-23 Methods of attack 23-25 The notion of locus. The method of exhaus- tion. Reductio ad absurdum. Reduction. Analysis. The diorismus, or discussion Summary of the general characteristics of the Greek geometry 25—26 CHAPTER II THE WORK OF EUCLID AND HIS INFLUENCE ON THE SUBSEQUENT TEACHING OF GEOMETRY The Ei<Emknts of Euclid 27-31 The contributions by the earlier Greeks .... 27-28 Euclid's sequence of subject-matter. Points of de- parture from the Euclidean system 28 EucUd's sequence not the historic 28-29 The practical eliminated 29 Hypothetical constructions debarred 29 Euclid established a systematic method of proving propositions 29-30 Some adverse criticisms of Euclid 30 Summary of the three chief characteristics of the "Elements" 30—31 The Later Influence of Euclid 31-33 At Alexandria 31 With the Arabs. Translations 31—32 In Europe 32—33 Some translations of the "Elements" The use of Euclid in the medieval universities Later editions of Euclid CHAPTER III THE TEACHING OF GEOMETRY FROM EUCLID TO THE RISE OF THE CHRISTIAN SCHOOLS At Alexandria 34-39 Archimedes 34—36 His writings. Contributions to solid geometry. Value of TT. Use of methods already laid down. Founda- tions of the integral calculus. Geometric and me- chanical proofs. A recognition of the unity of the mathematical subjects Apollonius of Perga 36 His study of the conic sections. Relation to later teaching of elementary geometry At Alexandria after Apollonius 36—39 Applications of geometry to astronomy and surveying. Those who carried on this work. The beginnings of trigonometry . 36 Extension of spherical geometry by Menelaus. Also earlier by Theodosius . 36-37 Interest in EucHd . 37-38 The commentators, Heron, Pappus, Theon, Proclus Contents vii The writings of Hypsicles, Geminus, Demascius of Demascus Ptolemy and his interest in geometry Some phases of treatment of subject-matter in the practical writings mentioned that have an educa- tional significance 38 The geometric nomenclature and symbolism of Heron. His treatment of the mensuration of heights and distances The ORIENTAI.S 39-40 The Hindus 39 Brahmagupta. His differentiation of "gross" answers from exact answers. Aryabhatta's brevity of proof. The use of verse The Arabs 39-40 Translators and preservers of Euclid and of Greek learning in general The Romans 40-42 Land surveying. The Codex Arcerianus Influence of the Alexandrian school Little influence of Euclid. Quintilian's estimate of logical g;eometry Summary showing the later influence on teaching ... 42 CHAPTER IV THE TEACHING OF GEOMETRY FROM THE RISE OF THE CHRISTIAN SCHOOLS TO THE YEAR 1525 The Christian Schools of the Middle Ages 43-47 The works of Capella, Boethius, Isidore of Seville, Cassi- odorus, and their use in the schools 43-44 The teaching of geometry in the medieval schools before Gerbert 45 The influence of Gerbert. His geometry 45-47 Summary 4? Books on Practical Geometry before the Rise of the Universities. Books that Influenced the University Teaching 47-50 Leonardo of Pisa. Savasorda. Jordanus Nemorarius. Robertus Anglicus. Sacrobosco. Bradwardine. Regiomontanus. Educational significance of their writings The Universities of the Middle Ages 51-53 Geometry taught before the introduction of Euclid ... 51 The teaching of Euclid 51-53 At Paris, Oxford, Prague, Vienna, Heidelberg, Cologne, Leipzig, Bologna, and Pisa. Character of the teaching CHAPTER V THE TEACHING OF GEOMETRY FROM THE YEAR 1525 TO THE PRESENT TIME Some Early Printed Books on Geometry 55-59 Paciuolo. Fineus. Instruments employed in field work. Bartoli. Cataneo. Belli. GargioUi. Gloriosus. The viii Contents influence of Albrecht Diirer. Geometry of a single opening of the compasses Tendencies in the above works that have a bearing on teaching 59-60 Germany 60-73 The early universities 60—61 Place of geometry in the curriculum. Interest in Euclid 61-63 Geometry in the secondary schools of the sixteenth century . Geometry in the secondary schools of the seventeenth century 63-65 The influence of Comenius. The geometries of Schroter and Gruvius Geometry in the secondary schools of the eighteenth century 65-71 Importance of mathematics and science. The texts of Wolf, Kastner, and Sturm, and their influence. The Realschulen Geometry in the secondary schools of the nineteenth century 71—72 Reorganization of the Gymnasia of Prussia. Admis- sion to universities. General nature of the teaching of geometry and mathematics in general General resumi from the sixteenth century, showing the development of the teaching of geometry from the standpoint of the curriculum and of method. Tendencies most prominent 72—73 France 73-87 General survey from the sixteenth century to the middle of the eighteenth 73-74 Early books that influenced teaching 74—78 Bouvelles. Ramus. Errard. Mercator. Arnauld. Le Clerc. The interest in the teaching of geometry up to the time of the expulsion of the Jesuits The eighteenth century 78-81 General survey. Use of texts in class work. Books of Rivard, Clairaut, and La Caille. Features with educational significance. The military schools and texts used in them Legendre and his influence 81—82 The teaching of geometry in France since Legendre . 83—86 Founding of the government schools. The lyc^es. Suggestions on teaching by Lacroix. By Busset Summary 86—87 England 87-90 In the universities 87—88 The thirteenth century. The fifteenth century. First English translation of Euclid. Professorships of mathematics at Oxford and Cambridge. Euclid's "Elements" edited by Barrow, Wliiston, Simson, Gregory. In later times by Playfair and Todhunter. The traditions Euclidean Transition of geometry into the secondary schools . 88-89 Summary 89—90 Russia 90-93 Before the creation of the Gymnasia 90 The beginning practical. Influence of Peter the Great in establishing special schools where mathematics was taught. Methods employed in these Founding of the Gymnasia 91-92 Aim to develop pure science.
Load more

Recommended publications
  • Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
    Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non­ L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non­ sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission.
    [Show full text]
  • Can One Design a Geometry Engine? on the (Un) Decidability of Affine
    Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A.
    [Show full text]
  • He One and the Dyad: the Foundations of Ancient Mathematics1 What Exists Instead of Ininite Space in Euclid’S Elements?
    ARCHIWUM HISTORII FILOZOFII I MYŚLI SPOŁECZNEJ • ARCHIVE OF THE HISTORY OF PHILOSOPHY AND SOCIAL THOUGHT VOL. 59/2014 • ISSN 0066–6874 Zbigniew Król he One and the Dyad: the Foundations of Ancient Mathematics1 What Exists Instead of Ininite Space in Euclid’s Elements? ABSTRACT: his paper contains a new interpretation of Euclidean geometry. It is argued that ancient Euclidean geometry was created in a quite diferent intuitive model (or frame), without ininite space, ininite lines and surfaces. his ancient intuitive model of Euclidean geometry is reconstructed in connection with Plato’s unwritten doctrine. he model cre- ates a kind of “hermeneutical horizon” determining the explicit content and mathematical methods used. In the irst section of the paper, it is argued that there are no actually ininite concepts in Euclid’s Elements. In the second section, it is argued that ancient mathematics is based on Plato’s highest principles: the One and the Dyad and the role of agrapha dogmata is unveiled. KEYWORDS: Euclidean geometry • Euclid’s Elements • ancient mathematics • Plato’s unwrit- ten doctrine • philosophical hermeneutics • history of science and mathematics • philosophy of mathematics • philosophy of science he possibility to imagine all of the theorems from Euclid’s Elements in a Tquite diferent intuitive framework is interesting from the philosophical point of view. I can give one example showing how it was possible to lose the genuine image of Euclidean geometry. In many translations into Latin (Heiberg) and English (Heath) of the theorems from Book X, the term “area” (spatium) is used. For instance, the translations of X. 26 are as follows: ,,Spatium medium non excedit medium spatio rationali” and “A medial area does not exceed a medial area by a rational area”2.
    [Show full text]
  • Greece: Archimedes and Apollonius
    Greece: Archimedes and Apollonius Chapter 4 Archimedes • “What we are told about Archimedes is a mix of a few hard facts and many legends. Hard facts – the primary sources –are the axioms of history. Unfortunately, a scarcity of fact creates a vacuum that legends happily fill, and eventually fact and legend blur into each other. The legends resemble a computer virus that leaps from book to book, but are harder, even impossible, to eradicate.” – Sherman Stein, Archimedes: What Did He Do Besides Cry Eureka?, p. 1. Archimedes • Facts: – Lived in Syracuse – Applied mathematics to practical problems as well as more theoretical problems – Died in 212 BCE at the hands of a Roman soldier during the attack on Syracuse by the forces of general Marcellus. Plutarch, in the first century A.D., gave three different stories told about the details of his death. Archimedes • From sources written much later: – Died at the age of 75, which would put his birth at about 287 BCE (from The Book of Histories by Tzetzes, 12th century CE). – The “Eureka” story came from the Roman architect Vitruvius, about a century after Archimedes’ death. – Plutarch claimed Archimedes requested that a cylinder enclosing a sphere be put on his gravestone. Cicero claims to have found that gravestrone in about 75 CE. Archimedes • From sources written much later: – From about a century after his death come tales of his prowess as a military engineer, creating catapults and grappling hooks connected to levers that lifted boats from the sea. – Another legend has it that he invented parabolic mirrors that set ships on fire.
    [Show full text]
  • Some Curves and the Lengths of Their Arcs Amelia Carolina Sparavigna
    Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna To cite this version: Amelia Carolina Sparavigna. Some Curves and the Lengths of their Arcs. 2021. hal-03236909 HAL Id: hal-03236909 https://hal.archives-ouvertes.fr/hal-03236909 Preprint submitted on 26 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna Department of Applied Science and Technology Politecnico di Torino Here we consider some problems from the Finkel's solution book, concerning the length of curves. The curves are Cissoid of Diocles, Conchoid of Nicomedes, Lemniscate of Bernoulli, Versiera of Agnesi, Limaçon, Quadratrix, Spiral of Archimedes, Reciprocal or Hyperbolic spiral, the Lituus, Logarithmic spiral, Curve of Pursuit, a curve on the cone and the Loxodrome. The Versiera will be discussed in detail and the link of its name to the Versine function. Torino, 2 May 2021, DOI: 10.5281/zenodo.4732881 Here we consider some of the problems propose in the Finkel's solution book, having the full title: A mathematical solution book containing systematic solutions of many of the most difficult problems, Taken from the Leading Authors on Arithmetic and Algebra, Many Problems and Solutions from Geometry, Trigonometry and Calculus, Many Problems and Solutions from the Leading Mathematical Journals of the United States, and Many Original Problems and Solutions.
    [Show full text]
  • Post-Euclid Greek Mathematics
    Archimedes Apollonius and the Conics How Apollonius described and classified the conic sections Some high points of Greek mathematics after Euclid Algebra Through History October 2019 Algebra Through History Greek Math Post Euclid Archimedes Apollonius and the Conics How Apollonius described and classified the conic sections Outline 1 Archimedes 2 Apollonius and the Conics 3 How Apollonius described and classified the conic sections Algebra Through History Greek Math Post Euclid Archimedes Apollonius and the Conics How Apollonius described and classified the conic sections Who was Archimedes? Lived ca. 287 - 212 BCE, mostly in Greek city of Syracuse in Sicily Studied many topics in what we would call mathematics, physics, engineering (less distinction between them at the time) We don’t know much about his actual life; much of his later reputation was based on somewhat dubious anecdotes, e.g. the “eureka moment,” inventions he was said to have produced to aid in defense of Syracuse during Roman siege in which he was killed, etc. Perhaps most telling: we do know he designed a tombstone for himself illustrating the discovery he wanted most to be remembered for (discussed by Plutarch, Cicero) Algebra Through History Greek Math Post Euclid Archimedes Apollonius and the Conics How Apollonius described and classified the conic sections Figure: Sphere inscribed in cylinder of equal radius 3Vsphere = 2Vcyl and Asphere = Acyl (lateral area) Algebra Through History Greek Math Post Euclid Archimedes Apollonius and the Conics How Apollonius described and classified the conic sections Surviving works On the Equilibrium of Planes (2 books) On Floating Bodies (2 books) Measurement of a Circle On Conoids and Spheroids On Spirals On the Sphere and Cylinder (2 books) Algebra Through History Greek Math Post Euclid Archimedes Apollonius and the Conics How Apollonius described and classified the conic sections Surviving works, cont.
    [Show full text]
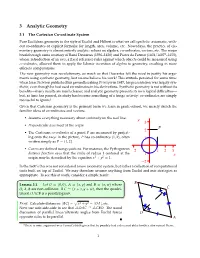
  • 3 Analytic Geometry
    3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2).
    [Show full text]
  • Synthetic and Analytic Geometry
    CHAPTER I SYNTHETIC AND ANALYTIC GEOMETRY The purpose of this chapter is to review some basic facts from classical deductive geometry and coordinate geometry from slightly more advanced viewpoints. The latter reflect the approaches taken in subsequent chapters of these notes. 1. Axioms for Euclidean geometry During the 19th century, mathematicians recognized that the logical foundations of their subject had to be re-examined and strengthened. In particular, it was very apparent that the axiomatic setting for geometry in Euclid's Elements requires nontrivial modifications. Several ways of doing this were worked out by the end of the century, and in 1900 D. Hilbert1 (1862{1943) gave a definitive account of the modern foundations in his highly influential book, Foundations of Geometry. Mathematical theories begin with primitive concepts, which are not formally defined, and as- sumptions or axioms which describe the basic relations among the concepts. In Hilbert's setting there are six primitive concepts: Points, lines, the notion of one point lying between two others (betweenness), congruence of segments (same distances between the endpoints) and congruence of angles (same angular measurement in degrees or radians). The axioms on these undefined concepts are divided into five classes: Incidence, order, congruence, parallelism and continuity. One notable feature of this classification is that only one class (congruence) requires the use of all six primitive concepts. More precisely, the concepts needed for the axiom classes are given as follows: Axiom class Concepts required Incidence Point, line, plane Order Point, line, plane, betweenness Congruence All six Parallelism Point, line, plane Continuity Point, line, plane, betweenness Strictly speaking, Hilbert's treatment of continuity involves congruence of segments, but the continuity axiom may be formulated without this concept (see Forder, Foundations of Euclidean Geometry, p.
    [Show full text]
  • Is Geometry Analytic? Mghanga David Mwakima
    IS GEOMETRY ANALYTIC? MGHANGA DAVID MWAKIMA 1. INTRODUCTION In the fourth chapter of Language, Truth and Logic, Ayer undertakes the task of showing how a priori knowledge of mathematics and logic is possible. In doing so, he argues that only if we understand mathematics and logic as analytic,1 by which he memorably meant “devoid of factual content”2, do we have a justified account of 3 a priori knowledgeδιανοια of these disciplines. In this chapter, it is not clear whether Ayer gives an argument per se for the analyticity of mathematics and logic. For when one reads that chapter, one sees that Ayer is mainly criticizing the views held by Kant and Mill with respect to arithmetic.4 Nevertheless, I believe that the positive argument is present. Ayer’s discussion of geometry5 in this chapter shows that it is this discussion which constitutes his positive argument for the thesis that analytic sentences are true 1 Now, I am aware that ‘analytic’ was understood differently by Kant, Carnap, Ayer, Quine, and Putnam. It is not even clear whether there is even an agreed definition of ‘analytic’ today. For the purposes of my paper, the meaning of ‘analytic’ is Carnap’s sense as described in: Michael, Friedman, Reconsidering Logical Positivism (New York: Cambridge University Press, 1999), in terms of the relativized a priori. 2 Alfred Jules, Ayer, Language, Truth and Logic (New York: Dover Publications, 1952), p. 79, 87. In these sections of the book, I think the reason Ayer chose to characterize analytic statements as “devoid of factual” content is in order to give an account of why analytic statements could not be shown to be false on the basis of observation.
    [Show full text]
  • A Diagrammatic Formal System for Euclidean Geometry
    A DIAGRAMMATIC FORMAL SYSTEM FOR EUCLIDEAN GEOMETRY A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy by Nathaniel Gregory Miller May 2001 c 2001 Nathaniel Gregory Miller ALL RIGHTS RESERVED A DIAGRAMMATIC FORMAL SYSTEM FOR EUCLIDEAN GEOMETRY Nathaniel Gregory Miller, Ph.D. Cornell University 2001 It has long been commonly assumed that geometric diagrams can only be used as aids to human intuition and cannot be used in rigorous proofs of theorems of Euclidean geometry. This work gives a formal system FG whose basic syntactic objects are geometric diagrams and which is strong enough to formalize most if not all of what is contained in the first several books of Euclid’s Elements.Thisformal system is much more natural than other formalizations of geometry have been. Most correct informal geometric proofs using diagrams can be translated fairly easily into this system, and formal proofs in this system are not significantly harder to understand than the corresponding informal proofs. It has also been adapted into a computer system called CDEG (Computerized Diagrammatic Euclidean Geometry) for giving formal geometric proofs using diagrams. The formal system FG is used here to prove meta-mathematical and complexity theoretic results about the logical structure of Euclidean geometry and the uses of diagrams in geometry. Biographical Sketch Nathaniel Miller was born on September 5, 1972 in Berkeley, California, and grew up in Guilford, CT, Evanston, IL, and Newtown, CT. After graduating from Newtown High School in 1990, he attended Princeton University and graduated cum laude in mathematics in 1994.
    [Show full text]
  • Apollonius Problem
    Journal of Computer-Generated Euclidean Geometry Apollonius Problem Deko Dekov Abstract. Given three non-intersecting circles, there are eight circles that are tangent to each of the given circles. We note that these eight circles form four pairs of circles such that the circles of a pair are inverses in the radical circle of the given three circles. The famous Apollonius problem includes the following problem: Given three non- intersecting circles, to construct all circles that are tangent to each of the given circles. There are eight total solutions. Construction of these eight circles, using the method due to Joseph Gergonne (1771-1859), is given, e.g. in Geometric Constructions [5]. Denote by 1 and 2 the Apollonius circles tangent respective externally and internally to the three given circles. If the given three circles are the three excircles of a given triangle, then circle 1 is the nine- point circle and circle 2 is the Apollonius circle of the given triangle. Paul Yiu [9] (see also Grinberg and Yiu [3]) noticed that the Apollonius circle of the given triangle is inverse image of the nine-point circle in the radical circle of the excircles. If the given three circles are the three Lucas circles of a given triangle, then circle 1 is the inner Soddy circle of the Lucas circles and circle 2 is the outer Soddy circle of the Lucas circles. In this case circle 2 coincides with the circumcircle of the given triangle. Peter Moses [6] noticed that the inner Soddy circle of the Lucas circles is the inverse image of the circumcircle of the given triangle.
    [Show full text]
  • Notes on Greek Mathematics
    MATHEMATICS IN ANCIENT GREECE Periods in Greek history [AG]. Archaic Period: 750 BC to 490 BC (Emergence of city- states to Battle of Marathon) The Iliad and the Odyssey were composed c. 750-720 (based on the `Trojan war’ of 1250-1225 BC.) Between 670-500 BC, many city-states were ruled by tyrants (a word borrowed into the Greek language from Asia Minor, to signify a man who seizes control of the state by a coup and governs illegally.) Classical Period: 490 to 323 BC (Battle of Marathon to death of Alexander). The years from 480 (Persians driven from Greece) to 430 saw the rise of Athenian democracy (under Pericles). The Parthenon was built, 447-432. Playwrights Sophocles, Aristophanes, Euripides were active in Athens (c. 430-400). Following undeclared war between Athens and Sparta from 460-445, the Peloponnesian war (431-404; account by Thucydides) kept these two states (and their allies throughout the region) busy. This led to the ascendance of Sparta and the `rule of thirty tyrants’ in Athens (404-403). Socrates was tried and executed in 399. His follower Plato wrote his dialogues (399-347) and founded the Academy. The accession of Philip II of Macedon (359) signals the beginning of a period of Macedonian rule. Philip invaded Asia in 336, and was assassinated the same year. His successor Alexander III (`the Great’, 356-323 BC) continued the program of world conquest over the next 13 years, invading India in 325 BC. Hellenistic Period (323-30 BC). Science, mathematics (Euclid) and culture flourished in Egypt (Alexandria) under the Ptolemaic dynasty.
    [Show full text]