DOCSLIB.ORG

Doubling the Cube: a New Interpretation of Its Significance for Early Greek Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Doubling the Cube: a New Interpretation of Its Significance for Early Greek Geometry HISTORIA MATHEMATICA 22 (1995), 119-137 Doubling the Cube: A New Interpretation of Its Significance for Early Greek Geometry KEN SAITO Faculty of Letters, Chiba University, Yayoi-cho, lnage-ku, Chiba, 263 Japan It is widely known that Hippocrates of Chios reduced the problem of doubling the cube to the problem of finding two mean proportionals between two given lines. Nothing, however, is known about how this reduction was justified. To answer this question, propositions and patterns of arguments in Books VI, XI, and XII of the Elements are examined. A reconstruction modelled after Archimedes' On Sphere and Cylinder, Proposition II-1, is proposed, and its plausibility is discussed. © 1995 AcademicPress, Inc. I1 est admis qu'Hippocrate de Chio a r6duit la duplication du cube au probl~me de la recherche de deux moyennes proportionnelles entre deux segments donn6s, mais rien n'est certain quant ~ la justification de cette r6duction. Pour r6pondre ~ cette question, sont exami- n6es les propositions comme les argumentations caract6ristiques des livres VI, XI, et XII des Elements. Une reconstruction sera propos6e d'apr~s De la sphere et du cylindre, proposition II-1 d'Archimbde, et son caract6re plausible sera discut6. © 1995 AcademicPress, Inc. Es ist wohlbekannt, daft Hippocrates von Chios das Problem der Verdoppelung des Wtirfels auf das Problem der Auffindung von zwei mittleren Proportionalen zwischen zwei gegebenen Geraden zurtickfiihrte. Jedoch ist nichts bekannt tiber die Rechffertigung dieser Reduktion. Um diese Frage zu beantworten, werden S~itze und Strukturen von Argumenten aus den Btichern VI, XI, und XII der Elemente untersucht. Eine Rekonstruktion wird dann vorgeschla- gen, die sich auf Satz II-1 in Archimedes Uber Kugel und Zylinder stiitzt, und ihre Plausibilitat wird diskutiert. © 1995 Academic Press, Inc. MSC 1991 subject classifications: 01A20, 51-03. KEY WORDS: Theory of proportion, Euclid, Archimedes. 1. INTRODUCTION The problem of doubling the cube is one of the central problems in Greek mathematics. Since it attracted many mathematicians of the period, we possess exceptionally rich ancient materials on this problem. As is well known, Hippocrates of Chios (ft. ca. 440 B.C.) is said to have originated the tradition of investigating cube duplication. Several sources credit him with reducing this problem to another, that of finding two mean proportionals between two given lines. For example, in his commentary to Archimedes' On Sphere and Cylinder (hereafter SC), Eutocius cites Eratosthenes: And it was sought among the geometers in what way one could double the given solid, keeping it in the same shape, and they called this sort of problem the duplication of the cube. And when they all puzzled for a long time, Hippocrates of Chios first conceived that if, for two 119 0315-0860/95 $6.00 Copyright © 1995 by Academic Press, Inc. All rights of reproduction in any form reserved. 120 KEN SAITO HM 22 given lines, two mean proportionals were found in continued proportion, the cube will be doubled. Whence he turned his puzzle into another no less puzzling) Hereafter we call this transformation of cube duplication into the problem of finding two mean proportionals "Hippocrates' reduction." It was in this reduced form that the solution of cube duplication was sought during antiquity. The traditions of these ancient studies have recently been so thoroughly studied by Knorr [9, 11-153] that it seems as if nothing further could be teased out of the extant materials. In this article, however, we concentrate on a problem about which almost all the ancient sources are strangely taciturn: how cube duplication was reduced to finding two mean proportionals between two given lines. Strangely enough, in contrast to the abundance of solutions for inserting two mean proportionals, we have little testimony on how Hippocrates' reduction was proved in antiquity. No extant text explains how Hippocrates arrived at this reduction. It would therefore seem worth- while to try to understand the kind of arguments he was likely to have made. 2 Throughout this paper, we will be less concerned with the heuristic context that motivated Hippocrates' work than with the justification of the discovery, the proof of the equivalence of cube duplication to finding two mean proportionals. Our concern will lead us to propose a new interpretation of the status of the theory of proportion in the early stage of Greek mathematics, where we will highlight a group of propositions which may have served as a tool for problem-solving (including that of cube duplication) for the mathematicians of the period. 2. THE PROBLEM AND ITS REDUCTION First, let us briefly analyze the problem of doubling the cube, taking into account ancient testimonies and modern studies on its reduction. Cube duplication is a problem that appears to have been originally stated as follows: [CD] To find a cube which is twice as large (in size, not side) as a given one. Fairly early on, however, this problem was studied in the following generalized form: [CDx] To find a cube whose ratio to a given cube equals the ratio of two given lines (not necessarily in the ratio 2:1) (see also [8, 23]). This generalized problem was then reduced to the following problem: 1 [5, 3:88]. We cite Knorr's translation in [9, 147]. Knorr persuasively asserts the genuineness of Eratosthenes' accounts. See [8, 17-24] and [9, 131-153]. 2 It might be doubted if Hippocrates really proved the truth of his reduction, since Eratosthenes simply says that Hippocrates "first conceived" the truth of the reduction. Therefore, the reader with maximum reserve should read the phrase "Hippocrates' proof (or justification) of his reduction" in this paper as "the first rigorous proof of Hippocrates' reduction." This proof was surely found very soon, if not by Hippocrates himself, since it was concerned with such an important problem as cube duplication. Archytas already contrived a method to insert two mean proportionals [5, 3:84-88; 9, 100-110], so that we may assume that the proof was already available to Archytas. It seems to us that the attribution of both the discovery and the proof of the "reduction" to Hippocrates himself fits better with other testimonies which rank him as one of the great mathematicians of the period. HM 22 DOUBLING THE CUBE 121 [CDxr] To find two mean proportionals between two given lines. Thus given two lines a, b, one must find x, y, such that a : x = x : y = y : b. The last problem, [CDxr], was usually investigated by the ancients under the name of cube duplication, although strictly speaking, this only covers the case b = 2a. We have a few sources that demonstrate the truth of Hippocrates' reduction, and they are based on the use of the concept of triplicate ratio (as used in a proposition like Elements XI-33), or the compounding of ratios. We can confirm this in Diocles [15, 102], Pappus [6, 1:66-68] (see also [9, 90-91]) and Philoponus [18, 104-105] (for translation, see [9, 20]). We cannot, however, regard these argu- ments as reflecting the first proof of Hippocrates' reduction for reasons that will be explained below. Some of the modern reconstructions follow the same lines as these authors of late antiquity. For example, Knorr explains the equivalence of cube duplication [CDx] and its reduction [CDxr] as follows: If for any two given lines, A and B, we can insert the two mean proportionals, X and Y, then A : X = X : Y = Y: B. Thus, by compounding the ratios, one has (A : X) 3 = (A : X)(X : Y)(Y : B), that is, A 3 : X 3 = A : B. Thus, X will be the side of a cube in the given ratio (B : A) to the given cube (m3). [8, 23] In this passage, Knorr is less interested in restoring Hippocrates' line of thought than in convincing modern readers of the truth of Hippocrates' reduction. Indeed, he does not pretend to restore any ancient argument. Using modern notations, he assumes the equivalence of triplicate ratio with the operation of compounding the same ratio three times, 3 and he further assumes that the triplicate ratio of two lines is equal to the ratio of the cubes on them. The truth of the former, though evident to us, is not explicitly proved in the extant Elements, while the latter is a special case of Elements XI-33. 4 In earlier studies [12; 13], we have argued that the concepts of duplicate and triplicate ratio, as well as that of compound ratio, appear to have been relatively late arrivals in the corpus of Greek mathematics, and that the same holds true for Proposition XI-33. If this thesis is correct, then these notions were certainly not available to Hippocrates when he formulated his reduction of cube duplication. It would, therefore, be worthwhile to search for a proof without these notions. ~ In this context, we should note another way to formulate cube duplication which must have been clear to Greek geometers from the time of Hippocrates. The problem [CDx] can easily be represented in the following more geometric form: [CDxg] Given a rectangular prism on a square base, to find a cube equal to it. 3 Knorr is far from the first to make this assumption. For example Heath, in his account of Hippocrates' reduction, states that "Hippocrates could work with compound ratios" [3, 1: 200]. 4 Another modern reconstruction in [1, 57ff.] is based on the corollary of XI-33. 5 In this respect, two modern reconstructions [16, 119; 14, 128] are to be noted. These authors do not resort to multiplicate and compound ratios, but use instead more fundamental theorems. However, as they did not intend to offer historical reconstructions, they offered no textual evidence for these arguments.
Load more

Recommended publications
  • The Holistic Hippocrates: 'Treating the Patient, Not Just the Disease'
    King, Helen. "The Holistic Hippocrates: ‘Treating the Patient, Not Just the Disease’." Hippocrates Now: The ‘Father of Medicine’ in the Internet Age. London: Bloomsbury Academic, 2020. 133–154. Bloomsbury Collections. Web. 24 Sep. 2021. <http:// dx.doi.org/10.5040/9781350005921.ch-007>. Downloaded from Bloomsbury Collections, www.bloomsburycollections.com, 24 September 2021, 04:27 UTC. Copyright © Helen King 2020. You may share this work for non-commercial purposes only, provided you give attribution to the copyright holder and the publisher, and provide a link to the Creative Commons licence. 7 Th e Holistic Hippocrates: ‘Treating the Patient, N o t J u s t t h e D i s e a s e ’ I n t h i s fi nal chapter I want to look at the Hippocrates of today not through specifi c uses in news stories or in quotes, but through the invocation of his name in holistic (or, as we shall see, ‘wholistic’) medicine. Holism today presents itself as a return to a superior past, and brings Hippocrates in as part of this strategy. Th e model of the history of medicine implicit – or sometimes explicit – in holistic users of Hippocrates is one in which there was a golden age until ‘the turn away from holism in medicine allowed diseases to be located in specifi c organs, tissues or cells’.1 While there is something in this where ancient medicine is concerned, with its basis in fl uids rather than organs, this is of course also a tried and tested strategy for convincing an audience of the value of a ‘new’ thing: you claim it is ‘old’, or ancient, or just traditional.
    [Show full text]
  • Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
    Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non­ L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non­ sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission.
    [Show full text]
  • Squaring the Circle a Case Study in the History of Mathematics the Problem
    Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A.
    [Show full text]
  • Plato As "Architectof Science"
    Plato as "Architectof Science" LEONID ZHMUD ABSTRACT The figureof the cordialhost of the Academy,who invitedthe mostgifted math- ematiciansand cultivatedpure research, whose keen intellectwas able if not to solve the particularproblem then at least to show the methodfor its solution: this figureis quite familiarto studentsof Greekscience. But was the Academy as such a centerof scientificresearch, and did Plato really set for mathemati- cians and astronomersthe problemsthey shouldstudy and methodsthey should use? Oursources tell aboutPlato's friendship or at leastacquaintance with many brilliantmathematicians of his day (Theodorus,Archytas, Theaetetus), but they were neverhis pupils,rather vice versa- he learnedmuch from them and actively used this knowledgein developinghis philosophy.There is no reliableevidence that Eudoxus,Menaechmus, Dinostratus, Theudius, and others, whom many scholarsunite into the groupof so-called"Academic mathematicians," ever were his pupilsor close associates.Our analysis of therelevant passages (Eratosthenes' Platonicus, Sosigenes ap. Simplicius, Proclus' Catalogue of geometers, and Philodemus'History of the Academy,etc.) shows thatthe very tendencyof por- trayingPlato as the architectof sciencegoes back to the earlyAcademy and is bornout of interpretationsof his dialogues. I Plato's relationship to the exact sciences used to be one of the traditional problems in the history of ancient Greek science and philosophy.' From the nineteenth century on it was examined in various aspects, the most significant of which were the historical, philosophical and methodological. In the last century and at the beginning of this century attention was paid peredominantly, although not exclusively, to the first of these aspects, especially to the questions how great Plato's contribution to specific math- ematical research really was, and how reliable our sources are in ascrib- ing to him particular scientific discoveries.
    [Show full text]
  • 15 Famous Greek Mathematicians and Their Contributions 1. Euclid
    15 Famous Greek Mathematicians and Their Contributions 1. Euclid He was also known as Euclid of Alexandria and referred as the father of geometry deduced the Euclidean geometry. The name has it all, which in Greek means “renowned, glorious”. He worked his entire life in the field of mathematics and made revolutionary contributions to geometry. 2. Pythagoras The famous ‘Pythagoras theorem’, yes the same one we have struggled through in our childhood during our challenging math classes. This genius achieved in his contributions in mathematics and become the father of the theorem of Pythagoras. Born is Samos, Greece and fled off to Egypt and maybe India. This great mathematician is most prominently known for, what else but, for his Pythagoras theorem. 3. Archimedes Archimedes is yet another great talent from the land of the Greek. He thrived for gaining knowledge in mathematical education and made various contributions. He is best known for antiquity and the invention of compound pulleys and screw pump. 4. Thales of Miletus He was the first individual to whom a mathematical discovery was attributed. He’s best known for his work in calculating the heights of pyramids and the distance of the ships from the shore using geometry. 5. Aristotle Aristotle had a diverse knowledge over various areas including mathematics, geology, physics, metaphysics, biology, medicine and psychology. He was a pupil of Plato therefore it’s not a surprise that he had a vast knowledge and made contributions towards Platonism. Tutored Alexander the Great and established a library which aided in the production of hundreds of books.
    [Show full text]
  • Hippocrates: Facts and Fiction 1. Introduction
    Acta Theologica Supplementum 7 2005 HIPPOCRATES: FACTS AND FICTION ABSTRACT Hippocrates, the Father of Medicine, is reviewed as a historical person and in terms of his contribution to medicine in order to distinguish fact from fiction. Contem- porary and later sources reveal that many (possibly untrue) legends accumulated around this enigmatic figure. The textual tradition and the composition of the so- called Corpus Hippocraticum, the collection of medical works written mainly in the 5th and 4th centuries BC (of which possibly only about five can be ascribed to Hip- pocrates himself) are discussed. The origin of the Hippocratic Oath, and the impact of the Hippocratic legacy on modern medicine are considered. 1. INTRODUCTION This article considers the historicity of Hippocrates, the Father of Me- dicine, distinguishes fact from fiction and assesses his contribution to the discipline in the context of the many myths, which are shown by both contemporary and later sources to have arisen about this enig- matic figure. The textual transmission and compilation of the Corpus Hippocraticum, a collection of medical texts written mainly in the 5th and 4th centuries BC (of which only perhaps five can be ascribed to Hippocrates with any degree of certainty), will also be discussed. Fi- nally, the origin of the Hippocratic Oath and the value of the Hippo- cratic legacy to modern medicine will be examined. Hippocrates has enjoyed unrivalled acclaim as the Father of Medi- cine for two and a half millennia. Yet he is also an enigmatic figure, and there is much uncertainty about his life and his true contribution to medicine.
    [Show full text]
  • ANCIENT PROBLEMS VS. MODERN TECHNOLOGY 1. Geometric Constructions Some Problems, Such As the Search for a Construction That Woul
    ANCIENT PROBLEMS VS. MODERN TECHNOLOGY SˇARKA´ GERGELITSOVA´ AND TOMA´ Sˇ HOLAN Abstract. Geometric constructions using a ruler and a compass have been known for more than two thousand years. It has also been known for a long time that some problems cannot be solved using the ruler-and-compass method (squaring the circle, angle trisection); on the other hand, there are other prob- lems that are yet to be solved. Nowadays, the focus of researchers’ interest is different: the search for new geometric constructions has shifted to the field of recreational mathematics. In this article, we present the solutions of several construction problems which were discovered with the help of a computer. The aim of this article is to point out that computer availability and perfor- mance have increased to such an extent that, today, anyone can solve problems that have remained unsolved for centuries. 1. Geometric constructions Some problems, such as the search for a construction that would divide a given angle into three equal parts, the construction of a square having an area equal to the area of the given circle or doubling the cube, troubled mathematicians already hundreds and thousands of years ago. Today, we not only know that these problems have never been solved, but we are even able to prove that such constructions cannot exist at all [8], [10]. On the other hand, there is, for example, the problem of finding the center of a given circle with a compass alone. This is a problem that was admired by Napoleon Bonaparte [11] and one of the problems that we are able to solve today (Mascheroni found the answer long ago [9]).
    [Show full text]
  • Modern Commentaries on Hippocrates1
    MODERN COMMENTARIES ON HIPPOCRATES1 By JONATHAN WRIGHT, M.D. PLEASANTVILLE, N. Y. PART I ERHAPS it is not the only way, but disturb us if Plato is thought by the young one of the ways of judging of the lady at the library to have written some­ excellence of a work of science or thing on astronomy or if the man who literature is to take note of the preaches in our church thinks Aristotle discussion the author has elicited in wasless a monk. We ourselves may be unable talentedP readers and the stimulation of to get up any enthusiasm for either. But the faculties thereby evidenced. In the when we learn that all these men have by conceit and braggadocio of Falstaff, aside their words tapped the ocean of thought in from his being the butt of jokes, we every era of civilization since they lived perceive he is conscious of the quality of and at their magic touch abundant streams his mind when he says he is not only witty of mental activity have gone forth to enrich himself, but is the cause of wit in others. the world, when we once realize what an There is no standard of truth whereby ever living power they still exercise over the the accuracy of theory and practice of one best minds which humanity produces, then age can be judged by another, though there what Dotty says about Ibsen or what Bill are underlying general principles which per­ Broker thinks of Kipling, that the Reverend sist as much perhaps by their vagueness Mr.
    [Show full text]
  • Can One Design a Geometry Engine? on the (Un) Decidability of Affine
    Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A.
    [Show full text]
  • A Concise History of the Philosophy of Mathematics
    A Thumbnail History of the Philosophy of Mathematics "It is beyond a doubt that all our knowledge begins with experience." - Imannuel Kant ( 1724 – 1804 ) ( However naïve realism is no substitute for truth [1] ) [1] " ... concepts have reference to sensible experience, but they are never, in a logical sense, deducible from them. For this reason I have never been able to comprehend the problem of the á priori as posed by Kant", from "The Problem of Space, Ether, and the Field in Physics" ( "Das Raum-, Äether- und Feld-Problem der Physik." ), by Albert Einstein, 1934 - source: "Beyond Geometry: Classic Papers from Riemann to Einstein", Dover Publications, by Peter Pesic, St. John's College, Sante Fe, New Mexico Mathematics does not have a universally accepted definition during any period of its development throughout the history of human thought. However for the last 2,500 years, beginning first with the pre - Hellenic Egyptians and Babylonians, mathematics encompasses possible deductive relationships concerned solely with logical truths derived by accepted philosophic methods of logic which the classical Greek thinkers of antiquity pioneered. Although it is normally associated with formulaic algorithms ( i.e., mechanical methods ), mathematics somehow arises in the human mind by the correspondence of observation and inductive experiential thinking together with its practical predictive powers in interpreting future as well as "seemingly" ephemeral phenomena. Why all of this is true in human progress, no one can answer faithfully. In other words, human experiences and intuitive thinking first suggest to the human mind the abstract symbols for which the economy of human thinking mathematics is well known; but it is those parts of mathematics most disconnected from observation and experience and therefore relying almost wholly upon its internal, self - consistent, deductive logics giving mathematics an independent reified, almost ontological, reality, that mathematics most powerfully interprets the ultimate hidden mysteries of nature.
    [Show full text]
  • Thales of Miletus Hippocrates I Replaced Superstition with Science. I
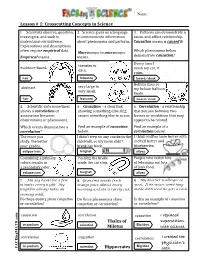
    ® Name: ____________________ Lesson # 1: Crosscutting Concepts in Science hb g7fcj 1. Scientists observe, question, 2. Science gives us a language 3. Patterns can demonstrate a investigate, and seek to to communicate information cause-and-effect relationship. understand our universe. about phenomena and patterns. Causation means a caused b. Explanations and descriptions often require empirical data. Which phenomena below Macroscopic to microscopic Empirical means… means… demonstrate causation? Every time I theories to evidence-based. wash my car, it data. rains. hair features beard/cloak Helium rises so very large to abstract. my helium balloon very small. floats. hair features beard/cloak 4. Scientific data sometimes 5. Causation – a clear link 6. Correlation - a relationship shows a correlation or showing something directing that you see between two association between causes something else to occur. factors or conditions that may observations or phenomena. appear to be related. Which events demonstrate a Find an example of causation Find an example of a correlation? below. correlation below. The more you I didn’t step on any cracks in the I think waffles taste better with study, the better sidewalk, so my mom didn’t melted butter and your grades. break her back. blueberries. eclipse icon magnet olives Combining 2 primary Pushing the brake People who watch lots colors results in made the car stop. of television eat lots a secondary color. of junk food. magnet eclipse icon olives 7. My dog barks for a few 8. Grandma drinks fresh 9. My brother is allergic to minutes every night. My orange juice almost every wool. If he wears something neighbor always takes an morning and she is rarely sick.
    [Show full text]
  • Pappus of Alexandria: Book 4 of the Collection
    Pappus of Alexandria: Book 4 of the Collection For other titles published in this series, go to http://www.springer.com/series/4142 Sources and Studies in the History of Mathematics and Physical Sciences Managing Editor J.Z. Buchwald Associate Editors J.L. Berggren and J. Lützen Advisory Board C. Fraser, T. Sauer, A. Shapiro Pappus of Alexandria: Book 4 of the Collection Edited With Translation and Commentary by Heike Sefrin-Weis Heike Sefrin-Weis Department of Philosophy University of South Carolina Columbia SC USA [email protected] Sources Managing Editor: Jed Z. Buchwald California Institute of Technology Division of the Humanities and Social Sciences MC 101–40 Pasadena, CA 91125 USA Associate Editors: J.L. Berggren Jesper Lützen Simon Fraser University University of Copenhagen Department of Mathematics Institute of Mathematics University Drive 8888 Universitetsparken 5 V5A 1S6 Burnaby, BC 2100 Koebenhaven Canada Denmark ISBN 978-1-84996-004-5 e-ISBN 978-1-84996-005-2 DOI 10.1007/978-1-84996-005-2 Springer London Dordrecht Heidelberg New York British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Library of Congress Control Number: 2009942260 Mathematics Classification Number (2010) 00A05, 00A30, 03A05, 01A05, 01A20, 01A85, 03-03, 51-03 and 97-03 © Springer-Verlag London Limited 2010 Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms of licenses issued by the Copyright Licensing Agency.
    [Show full text]