DOCSLIB.ORG

Raman Spectroscopy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Raman Spectroscopy Raman spectroscopy 1 1. DESCRIPTION OF THE RAMAN EXPERIMENT 1.1 General Description Raman spectroscopy is a technique for observing vibrational, rotational, electronic and other low-frequency modes in a system. It relies on inelastic scattering (i.e Raman scattering) of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range. The laser light indices transitions between different energy states in crystals or molecules, resulting in an energy loss (Stokes process) or an energy gain (anti-Stokes process) in the scattered light [1]. These energy shifts of the photons correspond to specific excitations in a material. They are detected by a special optical spectrometer. Light can interact with matter in a number of different ways. Refraction, reflection and absorption, that you are familiar with, are the most common ones. Refracted light changes direction, which is used in lens and prism optics. Absorbed photons disappear, giving off their energy to the absorbing material. During reflection light bounces off the surfaces or interfaces of materials. When thinking of light in terms of photons, reflection from surfaces is a type of scattering. There are other types. You are probably familiar with Compton scattering when high energy photons scatter from free electrons exchanging energy and momentum with them. This lab focuses on Raman scattering, where visible light interacts with crystals while exchanging energy with them. The simplest (but not quite correct as described below) way to understand Raman scattering is to imagine that a photon gives off some but not all of its energy to the material. In the process the photons do not disappear, but loose or gain some energy, i.e. they change their wavelength. By measuring the spectrum of the Raman-scattered light one can learn a great deal about the excitation spectrum of the material. Raman scattering is used widely in chemistry to identify materials based on their Raman spectra. In physics Raman scattering is used for investigating a wide variety of materials. It provides information about how atoms vibrate and about electronic excitations. In this lab we will perform experiments on two quantum materials, Silicon, which is widely used in electronics and YBaCuO, which is closely related to high temperature superconductors. 2 1.2 Basic Theory Raman scattering can be understood on an intuitive level starting from basic quantum mechanics. Due to Heisenberg energy-time uncertainty principle, a photon can be absorbed without conservation of energy as long as it is emitted a short time after. This process is called virtual absorption and the shortly-lived (virtual) excited state is called the intermedi- ate state. Most photons that are absorbed like this are reemitted a very short time later with the same wavelength and no excitation in the material is created or destroyed in the end. This process is called Rayleigh scattering. It actually interferes with Raman measurements and Raman spectrometer we are going to use is designed to filter it out. During Raman scattering the intermediate virtual state is involved in the same way, but wavelength of the emitted photon is different from the incident one. In this case the energy has to be conserved between the initial and the final state, because both the incident and scattered photon have a long lifetime. In order to conserve energy an excitation is created inside the material. For example an electron can jump into a different orbital or an atomic lattice vibration is induced or annihilated. The energy of this excitation must equal to the difference between the incident and scattered photon. If there is no excitation that would satisfy this rule, then the scattering process is impossible. Therefore, Raman scattering can occur only if the difference between the incident and scattered photon energies is equal to the energy of an excitation inside the material. Let's see how this works starting from the quantum mechanical Hamiltonian describing the interaction of light with electrons. If you don't understand the following equations, you will still be able to do the lab. First, consider the coupling between photons and electrons. The hamiltionian is shown as follows [2][3]: ^ 2 X [^pi + eA(~ri; t)=c] H^ = = H^ + H^ + H^ (1) 2m 0 1 2 i ^ 2 2 Z 2 X [eA(~ri; t)=c] e H^ = = d~rρ(~r) A^(~r ; t) (2) 1 2m 2mc2 i i X e e Z H^ = (^p · A^(~r ; t) + A^(~r ; t) · p^ ) = d~r^j(~r) · A^(~r; t); (3) 2 2mc i i i i c i ^ wherep ^i is the momentum operator, A(~ri; t) is the electromagnetic vector potential, P ^ charge density operator ρ(~r) = i δ(~r − ~ri), electron particle current operator j(~r) = 3 P p^iδ(~r−~ri)+δ(~r−~ri)^pi i 2m , and sum is over all electrons and we omit the term without the vector potential. As a result of one scattering event, the scattering medium makes a transition from state jii to state jfi and the laser light from jNLki to jNLk − 1;NSk0 = 1i. Here L and S are the polarization of light and k is the wavevector. Let X denote the Raman active excitation. If X is coupled to ~ρ(~r) and ~j(~r) and satisfies the symmetry requirements (see section 1.5), it will be Raman active. From perturbation theory, in the absence of a significant number of photons in the scattered channel, we get the following second order scattering cross section: d2σ ! !3 n V 2 L S S X −βi 2 = 4 e jhfj χLS jiij δ(!L − !S − !) (4) d!dΩ nLc i;f in which 2 ~ ~ ~ ~ ~ ~ ~ ~ V e X hfj j(kS) · ~eS jmi hmj j(−kL) · ~eL jii hfj j(−kL) · ~eL jmi hmj j(−kS) · ~eS jii hfj χ jii = ( + ) LS ! ! ! − ! − ! − iη ! − ! + ! − iη L S m m i L m i L e2 − me!L!S~eL · ~eS hfj ρ(−~q) jii (5) ^ ^ where H1 contributes to the first order expansion and H2 to the second order term, ~eL and ~eS are polarization vectors of the incident and scattered photons respectively, !L and !S are their frequencies, jii ; jfi and jmi are the initial, final and (virtual) intermediate electronic states of second order perturbation theory, and !i;!f and !m are their energies. η is a positive infinitesimal, which is replaced by the damping parameter for state jmi, where appropriate nL and nS are the refractive index at !L and !S, me is the mass of the electron. 1.3 Notation for describing polarization geometries Notation for describing the result of a Raman experiment is a(bc)d, where a(d) is direction of momentum of incident (scattered) photons, and b(c) is the direction of polarization of incident (scattered) photons. For example, z(xy)¯z means that momentum of the incident photon is in the z direction, of scattered photon in the z direction; incident photon is polarized along x, scattered along y. In our experiment we use a quasi backscattering geometry, so the polarization configuration is z(ab)¯z. We just use ab below for simplicity. 4 1.4 Resonant Raman Scattering From equation (5), when either of the denominators goes to zero, we will get the resonant Raman Scattering. At the resonance condition, Raman signals are greatly enhanced. 1.5 Selection Rules Crystals are highly symmetric. There are two types of symmetries in crystals: Discrete translational symmetry and discrete point group symmetry. The translational symmetry means that certain translations take the crystal into itself. In addition certain rotations reflections, and inversion performed while keeping one point fixed also take the crystal into itself. For example, in a simple cubic crystal 90 degree rotations around any one atomic position take the crystal into itself, etc. Turns out that these symmetry operations have deep consequences for the physical properties of materials, including for what is observed in the Raman spectra. The formal theory is rather involved and is outside the scope of this lab. For our purposes it is important to realize that the wavelength of both incident and outgoing light is much longer than the interatomic distances, so one can think of every unit cell sitting in the oscillating effectively spatially uniform electric field of the incident light plus the electric field of the Raman-scattered light. Now, for example, consider an atomic vibration in a crystal with inversion symmetry induced by the Raman process. Inversion takes the equilibrium structure into itself, however, if you think of the phonon as a deviation from the equilibrium structure, inversion can take the phonon into minus itself (odd phonon) or into itself (even phonon) depending on the specifics of how the atoms vibrate. Photons in the incident and scattered light together are even under inversion, because the relative angle between their polarizations does not change. The scattering process starts out with the incident electric field only, and ends with the phonon and scattered electric field. But the symmetry of the entire system (electric field plus crystal) has to remain the same before and after scattering. Let's consider, for example, inversion. Originally, crystal is even under inversion and the incident electric field is odd, so the total system before scattering is odd under inversion. After the scattering, if the phonon is even under inversion, the system is still odd (because the scattered photon is odd), so this scattering process is allowed. If 5 the phonon is odd under inversion, then the symmetry after scattering is even, and such a process is forbidden. Each symmetry operation of the crystal imposes strict constraints on which incident/scattered photon polarization allows scattering from which phonons.
Load more

Recommended publications
  • Raman Scattering and Fluorescence
    Fluorescence 01 Raman Scattering and Fluorescence Introduction The existence of such virtual states also explains why the non-resonance Raman effect Raman scattering and Fluorescence emission does not depend on the wavelength of the are two competing phenomena, which have excitation, since no real states are involved in similar origins. Generally, a laser photon this interaction mechanism. In fact, the Raman bounces off a molecule and looses a certain spectrum generally does not depend on the amount of energy that allows the molecule to laser excitation. vibrate (Stokes process). The scattered photon is therefore less energetic and the associated However, when the energy of the excitation light exhibits a frequency shift. The various photon gets close to the transition energy frequency shifts associated with different between two electronic states, one then deals molecular vibrations give rise to a spectrum, with resonance Raman or resonance that is characteristic of a specific compound. fluorescence (fig.1, case (d)). The basic difference between these two processes is In contrast, fluorescence or luminescence related to the time scales involved, as well as emission follows an absorption process. For a with the nature of the so-called intermediate better understanding, one can refer to the states. In contrast with resonant fluorescent, diagram below. relaxed fluorescence results from the emission of a photon from the lowest vibrational level of an excited electronic state, following a direct absorption of the photon and relaxation of the molecule from its vibrationally excited level of the electronic state back to the lowest vibrational level of the electronic state. A fluorescence process typically requires more than 10-9 s.
    [Show full text]
  • Article Intends to Provide a for the Necessary Virtual Electronic Brief Overview of the Differences and Transition
    ADVANCES IN RAMAN TECHNIQUES Laser requirements and advances for Raman techniques Andreas Isemann Laser Quantum GmbH, 78467 Konstanz, Germany INTRODUCTION 473 nm and 1064 nm, a narrow Raman scattering as a probe of bandwidth output of few tens of GHz vibrational transitions has made or below 1 MHz if needed within the leaps and bounds since its discovery, linewidth of vibrational transitions and various schemes based on this for high resolution, low noise (less phenomenon have been developed than 0.02%) and excellent beam with great success. quality (fundamental transversal Applications range from basic electromagnetic mode TEM00) scientific research, to medical and provides optimised performance industrial instrumentation. Some for the resolution of the Raman schemes utilise linear Raman measurement needed. scattering, whilst others take advantage The wavelength is chosen based of high peak-power fields to probe on the sample under investigation, nonlinear Raman responses. with 532 nm being commonly used This article intends to provide a for the necessary virtual electronic brief overview of the differences and transition. In the following section, benefits, together with the laser source four examples from different areas of requirements and the advancements Raman applications show the diverse in techniques enabled by recent applications of linear Raman and what developments in lasers. advances have been achieved. An example of studying a real-world LINEAR RAMAN application, the successful control of Figure 1 An example of the RR microfluidic device counting of The advent of the laser in providing a food quality using Raman spectroscopy photosynthetic microorganisms. As the cells of the model strain high-intensity coherent light source and multivariate analysis, is described Synechocystis sp.
    [Show full text]
  • High Performance Raman Spectroscopy with Simple Optical Components ͒ ͒ W
    High performance Raman spectroscopy with simple optical components ͒ ͒ W. R. C. Somerville, E. C. Le Ru,a P. T. Northcote, and P. G. Etchegoinb The MacDiarmid Institute for Advanced Materials and Nanotechnology, School of Chemical and Physical Sciences, Victoria University of Wellington, P.O. Box 600, Wellington, New Zealand ͑Received 6 December 2009; accepted 19 April 2010͒ Several simple experimental setups for the observation of Raman scattering in liquids and gases are described. Typically these setups do not involve more than a small ͑portable͒ CCD-based spectrometer ͑without scanning͒, two lenses, and a portable laser. A few extensions include an inexpensive beam-splitter and a color filter. We avoid the use of notch filters in all of the setups. These systems represent some of the simplest but state-of-the-art Raman spectrometers for teaching/ demonstration purposes and produce high quality data in a variety of situations; some of them traditionally considered challenging ͑for example, the simultaneous detection of Stokes/anti-Stokes spectra or Raman scattering from gases͒. We show examples of data obtained with these setups and highlight their value for understanding Raman spectroscopy. We also provide an intuitive and nonmathematical introduction to Raman spectroscopy to motivate the experimental findings. © 2010 American Association of Physics Teachers. ͓DOI: 10.1119/1.3427413͔ I. INTRODUCTION and finish with a higher energy than the original one. This case corresponds to anti-Stokes Raman scattering. The Raman effect was discovered in 1928 by Raman1 and In reality, the photon is usually provided by a laser, which is now a major research tool with applications in physics, has a well defined frequency.
    [Show full text]
  • 22 DE88 014566 Introduction
    Influence of stimulated Raman scattering on the CONF-880435 — 22 conversion efficiency in four wave mixing DE88 014566 Rainer Wunderlich Max-Planck-Institut fur Kernphysik D6900 Heidelberg l.FRG M. A. Moore, W. R. Garrett and M. G. Payne Chemical Physics Section, Oak Ridge National Laboratory Oak Ridge ,TN 37831 USA Abstract: Secondary nonlinear optical effects following parametric four wave mixing in •odium vapor are investigated. The generated ultraviolet radiation induces stimulated Raman scattering and other four wave mixing process. Population transfer due to Raman transitions strongly influences the phase matching conditions for the primary mixing process. Pulse shortening and a reduction in conversion efficiency are observed. Introduction Tunable light sources in the ultraviolet (UV) and vacuum ultraviolet (VUV) region of the optical spectrum are important tools for the resonant excitation and ionisation of atoms and moleculs whose lowest excited states have energies above 6eV. Below 200nm tunable VUV light is most often produced by four wave mixing (FWM) in phase matched ga» mixtures. The tuning range has been extended belcw lQOnm (Hilber et. al 1987) using Kr as nonlinear medium. The efficiency of UV generation is increased by choosing an active medium with resonance enhancement of the third order nonlinear susceptibilty ,x (wc/v)> at the particular wavelength. Here we are concerned with loss processes of the generated UV due to further nonlinear processes like stimulated electronic Raman scattering and four wave mixing processes initiated by the UV which do not directly involve the generation of the UV itself. Processes which directly limit UV generation depend on the resonance structure of x*3* [uuv) • In case of a two photon resonance pump depletion due to two photon absorption and ionisation, bleaching of x^3' («i/v") due to population transfer (Heinrich et al 1983) and population transfer induced index changes (Puell et al 1980) limit the UV generation.
    [Show full text]
  • Optics, Lasers, and Molecules: a Study of Raman Spectroscopy
    OPTICS, LASERS, AND MOLECULES: A STUDY OF RAMAN SPECTROSCOPY Stephen Carr, Mojin Chen, Brian Delancy, Jason Elefant, Alice Huang, Nathaniel May, Avinash Moondra, John Nappo, Nicholas Paggi, Samuel Rosin, Marlee Silverstein, Daniel Zhang Advisor: Dr. Robert Murawski Assistant: Aaron Loether ABSTRACT Raman spectroscopy is a technique that can be used to examine the rotational and vibrational states of a molecule, as well as the number, strength, and identity of chemical bonds. It is a process in which photons interact with a sample to produce scattered radiation of varying wavelengths. Spectroscopy has been widely used across various fields to identify water and air pollutants, in addition to proving useful with a multitude of other applications. In this study of optics, lasers, and molecules, Raman spectroscopy was used to analyze different samples of water to test for impurities and the presence of foreign molecules. Samples tested included alcohols, water, and fertilizer. From the data collected, the accuracy of the setups could be confirmed by comparing alcohol spectra to accepted Raman readings and identify additional chemical components in fountain water and Glaceau SmartWater, a brand of bottled water. In addition, samples of various concentrations of fertilizer were analyzed to verify major chemical components as well as relate the concentration and intensity of the Raman signal. INTRODUCTION/BACKGROUND Optics Optics is the study of light and its interactions with matter. Light, or electromagnetic radiation, exhibits both wave and particle properties, and this wave-particle duality is responsible for many of light’s behaviors. The wave-like properties of this electromagnetic radiation are exhibited in behaviors such as reflection (return of a wave from the original medium off an interface back into the original medium), refraction (bending of a wave as it passes from one index of refraction to another) and diffraction (bending of waves as it passes through openings).
    [Show full text]
  • Femtosecond Time-Resolved Four-Wave Mixing Applied to the Investigation of Excited State Dynamics
    Femtosecond Time-Resolved Four-Wave Mixing Applied to the Investigation of Excited State Dynamics by Vinu V. Namboodiri A thesis submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy in Physics Approved by the thesis Committee: (Prof. Dr. Arnulf Materny) (Prof. Dr. Ulrich Kleinekathöfer) (PD Dr. Michael Schmitt) Date of Defence: May 18, 2010 School of Engineering and Science Femtosecond Time-Resolved Four-Wave Mixing Applied to the Investigation of Excited State Dynamics Dedicated to my family, friends and Sreeappan Abstract Laser spectroscopy in the frequency domain has, very early, developed into a pow- erful tool for the analysis of structural properties of molecules. The development of ultrafast lasers added a new dimension to conventional spectroscopy by rendering time resolved measurements possible. The high time resolution offered by picosecond and femtosecond laser pulses enabled the real time observation of extremely fast pro- cesses, such as vibrations and rotations of molecules. With pulses of duration about 100 fs, it is now possible to monitor processes such as internal conversion, vibrational relaxation, and many other processes occurring in the excited electronic states which leads to reactive or energy transfer pathways. The work presented in this thesis fo- cuses on the study of molecular dynamics in these excited electronic states using time- resolved four-wave mixing (FWM) techniques. It is demonstrated that, by combining the FWM process with an excitation pulse, it is possible to study molecular dynamics in the excited states of gaseous and condensed phase samples. The advantages of the four-wave mixing technique over the commonly used time-resolved fluorescence and pump-probe techniques are also discussed.
    [Show full text]
  • Rayleigh and Raman Scattering from Alkali Atoms
    atoms Article Rayleigh and Raman Scattering from Alkali Atoms Adam Singor 1,* , Dmitry Fursa 1 , Keegan McNamara 2 and and Igor Bray 1 1 Curtin Institute for Computation and Department of Physics and Astronomy, Curtin University, Perth, WA 6102, Australia; [email protected] (D.F.); [email protected] (I.B.) 2 Institute for Theoretical Physics, ETH Zurich, 8093 Zürich, Switzerland; [email protected] * Correspondence: [email protected] Received: 14 August 2020; Accepted: 3 September 2020; Published: 7 September 2020 Abstract: Two computational methods developed recently [McNamara, Fursa, and Bray, Phys. Rev. A 98, 043435 (2018)] for calculating Rayleigh and Raman scattering cross sections for atomic hydrogen have been extended to quasi one-electron systems. A comprehensive set of cross sections have been obtained for the alkali atoms: lithium, sodium, potassium, rubidium, and cesium. These cross sections are accurate for incident photon energies above and below the ionization threshold, but they are limited to energies below the excitation threshold of core electrons. The effect of spin-orbit interaction, importance of accounting for core polarization, and convergence of the cross sections have been investigated. Keywords: rayleigh; raman; photon scattering; alkali; complex scaling 1. Introduction A fully quantum mechanical approach to photon-atom scattering processes has been well understood since the mid 1920’s with the development of the Kramers–Heisenberg–Waller (KHW) matrix elements [1,2]. The KHW matrix elements describe photon-atom interactions to second order in perturbation theory. Since then, photon-atom and photon-molecule scattering cross sections have proved to be essential for many applications, such as modelling opacity and radiative transport [3–5], Raman spectroscopy [6], and quantum illumination and radar [7,8].
    [Show full text]
  • Coherent Raman Scattering
    3 1. Theory of Coherent Raman Scattering Eric Olaf Potma and Shaul Mukamel 1.1 Introduction: The Coherent Raman Interaction ............................4 1.2 Nonlinear Optical Processes ...... .. .......... .... ... .. .... .... ...5 1.2.1 Induced Polarization ................ .. .... ... .. ..... ......... .5 1.2.2 Nonlinear Polarization .. .... .. ... .... .. ... ......... ..........6 1.2.3 Magnitude of the Optical Nonlinearity ..... ............ ...... .. ...7 1.3 Classification of Raman Sensitive Techniques . .. .... .. .... .. .... .. .. ... ..8 1.3.1 Coherent versus Incoherent .. .... .. .. .... .. .. ... .. ..............8 1.3.2 Linear versus Nonlinear . .. .. .. ..... ............... .. .... .... .8 1.3.3 Homodyne versus Heterodyne Detection ...........................9 1.3.4 Spontaneous versus Stimulated .................... .............10 1.4 Classical Description of Matter and Field: The Spontaneous Raman Effect. ...10 1.4.1 Electronic and Nuclear Motions .... .. ... ..... .... .... .. .... ..10 1.4.2 Spontaneous Raman Scattering Signal. .. ...... .... ... .. .... 12 1.5 Classical Description of Matter and Field: Coherent Raman Scattering .... ...13 1.5.1 Driven Raman Mode .... .. ... .. ... .... .. ... .. .......... ...... .14 1.5.2 Probe Modulation .. .................... ..... .. ...... .......15 1.5.3 Energy Flow in Coherent Raman Scattering ...... ..... .... ... .. ...17 1.6 Semi-Classical Description: Quantum Matter and Classical Fields ... .. .... .21 1.6.1 Wavefunctions of Matter ............. ... ........ .. ...
    [Show full text]
  • 4.6 Raman Spectroscopy
    4.6 Raman Spectroscopy R.H. ATALLA, U.P. AGARWAL, and J.S. BOND 4.6.1 Introduction Raman scattering was first observed in 1928 and was used to investigate the vibrational states of many molecules in the 1930s. Initially, spectroscopic methods based on the phenomenon were used in research on the structure of relatively simple molecules. Over the past 20 years, however, the development of laser sources and new generations of monochromators and detectors has made possible the application of Raman spectroscopy to the solution of many problems of technological interest. In many industrial laboratories, Raman spectroscopy is routinely used, together with infrared spectroscopy, for acquisition of vibrational spectra. Raman spectrometer systems for routine analytical applications are com- mercially available. An important expansion of the potential of the technique has arisen from the use of the microprobe, which permits acquisition of spectra from domains as small as one micron. Application of Raman spectroscopy to lignin analytical chemistry is rela- tively new, and only limited information has been obtained. However, the technique offers several potential advantages and, though it is complementary to infrared spectroscopy, it gives information that is not accessible with the latter alone. 4.6.2 Principle The phenomena underlying Raman spectroscopy can be described by com- parison with infrared spectroscopy as shown schematically in Fig. 4.6.1. The primary event in infrared absorption is the transition of a molecule from a ground state (M) to a vibrationally excited state (M*) by absorption of an infrared photon with energy equal to the difference between the energies of the ground and the excited states.
    [Show full text]
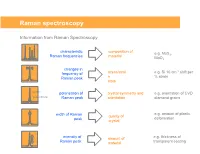
  • Raman Spectroscopy
    Raman spectroscopy Information from Raman Spectroscopy characteristic composition of e.g. MoS , Raman frequencies material 2 MoO3 changes in -1 frequency of stress/strai e.g. Si 10 cm shift per Raman peak n % strain state parallel polarisation of crystal symmetry and e.g. orientation of CVD perpendicular Raman peak orientation diamond grains e.g. amount of plastic width of Raman quality of deformation peak crystal intensity of amount of e.g. thickness of Raman peak material transparent coating Collecting the light The coupling of a Raman spectrometer with an optical microscope provides a number of advantages: 1) Confocal Light collection 2) High lateral spatial resolution 3) Excellent depth resolution 4) Large solid collection angle for the Raman light The basic function of a Raman system • Deliver the laser to the sampling point – With low power loss through the system – Illuminating an area consistent with sampling dimensions – Provide a selection/choice of laser wavelengths • Collect the Raman scatter – High aperture – High efficiency optics – High level of rejection of the scattered laser light • Disperse the scattered light – Short wavelength excitation requires high dispersion spectrometers • Detect the scattered light • Graphically / mathematically present the spectral data Laser wavelength selection concerns for classical Raman As the laser wavelength gets shorter Raman scattering efficiency increases The risk of fluorescence increases (except deep UV) The risk of sample damage / heating increases The cost of the spectrometer increases
    [Show full text]
  • What Is Raman Spectroscopy?
    What is Raman Spectroscopy? What is Raman Spectroscopy? Raman spectroscopy is an analytical technique where scattered light is used to measure the vibrational energy modes of a sample. It is named after the Indian physicist C. V. Raman who, together with his research partner K. S. Krishnan, was the first to observe Raman scattering in 1928.1 Raman spectroscopy can provide both chemical and structural information, as well as the identification of substances through their characteristic Raman ‘fingerprint’. Raman spectroscopy extracts this information through the detection of Raman scattering from the sample. What is Raman Scattering? When light is scattered by molecule, the oscillating electromagnetic field of a photon induces a polarisation of the molecular electron cloud which leaves the molecule in a higher energy state with the energy of the photon transferred to the molecule. This can be considered as the formation of a very short-lived complex between the photon and molecule which is commonly called the virtual state of the molecule. The virtual state is not stable and the photon is reemitted almost immediately, as scattered light. Figure 1 Three types of scattering processes that can occur when light interacts with a molecule. In the vast majority of scattering events, the energy of the molecule is unchanged after its interaction with the photon; and the energy, and therefore the wavelength, of the scattered photon is equal to that of the incident photon. This is called elastic (energy of scattering particle is conserved) or Rayleigh scattering and is the dominant process. In a much rarer event (approximately 1 in 10 million photons)2 Raman scattering occurs, which is an inelastic scattering process with a transfer of energy between the molecule and scattered photon.
    [Show full text]
  • Selecting an Excitation Wavelength for Raman Spectroscopy
    Electronically reprinted from March 2016 ® Molecular Spectroscopy Workbench Selecting an Excitation Wavelength for Raman Spectroscopy Were it not for the problem of photoluminescence, only one laser excitation wavelength would be neces- sary to perform Raman spectroscopy. Here, we examine the problem of photoluminescence from the material being analyzed and the substrate on which it is supported. We describe how to select an excita- tion wavelength that does not generate photoluminescence, reduces the noise level, and yields a Raman spectrum with a superior signal-to-noise ratio. Furthermore, we discuss the phenomenon of resonance Raman spectroscopy and the effect that laser excitation wavelength has on the Raman spectrum. David Tuschel ne of the most frequent questions that I hear from Another consideration when selecting an excitation people new to Raman spectroscopy is, “What laser wavelength can be the variation of the optical density of Oexcitation wavelength do I need?” Of course, the the material as a function of wavelength. If the material answer to that question is that it depends entirely upon the is transparent, then the depth of focus and focal volume materials one wishes to analyze. The Raman scattering of the laser beam will be dictated by the numerical aper- cross-section of the material is important and so too are its ture of the lens, the wavelength of the laser light, and the physical and optical properties. For example, if the sample real component of the sample’s refractive index at that is transparent to the excitation wavelength and thin enough, wavelength. However, if the sample is not transparent one can expect a spectral contribution from the substrate on (that is, the imaginary component of the refractive index which the sample is mounted or positioned.
    [Show full text]