Module 4. Understanding and Using Logs and Exponential Equations 4A
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

TI 83/84: Scientific Notation on Your Calculator
TI 83/84: Scientific Notation on your calculator this is above the comma, next to the square root! choose the proper MODE : Normal or Sci entering numbers: 2.39 x 106 on calculator: 2.39 2nd EE 6 ENTER reading numbers: 2.39E6 on the calculator means for us. • When you're in Normal mode, the calculator will write regular numbers unless they get too big or too small, when it will switch to scientific notation. • In Sci mode, the calculator displays every answer as scientific notation. • In both modes, you can type in numbers in scientific notation or as regular numbers. Humans should never, ever, ever write scientific notation using the calculator’s E notation! Try these problems. Answer in scientific notation, and round decimals to two places. 2.39 x 1016 (5) 2.39 x 109+ 4.7 x 10 10 (4) 4.7 x 10−3 3.01 103 1.07 10 0 2.39 10 5 4.94 10 10 5.09 1018 − 3.76 10−− 1 2.39 10 5 7.93 10 8 Remember to change your MODE back to Normal when you're done. Using the STORE key: Let's say that you want to store a number so that you can use it later, or that you want to store answers for several different variables, and then use them together in one problem. Here's how: Enter the number, then press STO (above the ON key), then press ALPHA and the letter you want. (The letters are in alphabetical order above the other keys.) Then press ENTER. -

Primitive Number Types
Primitive number types Values of each of the primitive number types Java has these 4 primitive integral types: byte: A value occupies 1 byte (8 bits). The range of values is -2^7..2^7-1, or -128..127 short: A value occupies 2 bytes (16 bits). The range of values is -2^15..2^15-1 int: A value occupies 4 bytes (32 bits). The range of values is -2^31..2^31-1 long: A value occupies 8 bytes (64 bits). The range of values is -2^63..2^63-1 and two “floating-point” types, whose values are approximations to the real numbers: float: A value occupies 4 bytes (32 bits). double: A value occupies 8 bytes (64 bits). Values of the integral types are maintained in two’s complement notation (see the dictionary entry for two’s complement notation). A discussion of floating-point values is outside the scope of this website, except to say that some bits are used for the mantissa and some for the exponent and that infinity and NaN (not a number) are both floating-point values. We don’t discuss this further. Generally, one uses mainly types int and double. But if you are declaring a large array and you know that the values fit in a byte, you can save ¾ of the space using a byte array instead of an int array, e.g. byte[] b= new byte[1000]; Operations on the primitive integer types Types byte and short have no operations. Instead, operations on their values int and long operations are treated as if the values were of type int. -

C++ Data Types
Software Design & Programming I Starting Out with C++ (From Control Structures through Objects) 7th Edition Written by: Tony Gaddis Pearson - Addison Wesley ISBN: 13-978-0-132-57625-3 Chapter 2 (Part II) Introduction to C++ The char Data Type (Sample Program) Character and String Constants The char Data Type Program 2-12 assigns character constants to the variable letter. Anytime a program works with a character, it internally works with the code used to represent that character, so this program is still assigning the values 65 and 66 to letter. Character constants can only hold a single character. To store a series of characters in a constant we need a string constant. In the following example, 'H' is a character constant and "Hello" is a string constant. Notice that a character constant is enclosed in single quotation marks whereas a string constant is enclosed in double quotation marks. cout << ‘H’ << endl; cout << “Hello” << endl; The char Data Type Strings, which allow a series of characters to be stored in consecutive memory locations, can be virtually any length. This means that there must be some way for the program to know how long the string is. In C++ this is done by appending an extra byte to the end of string constants. In this last byte, the number 0 is stored. It is called the null terminator or null character and marks the end of the string. Don’t confuse the null terminator with the character '0'. If you look at Appendix A you will see that the character '0' has ASCII code 48, whereas the null terminator has ASCII code 0. -

Floating Point Numbers
Floating Point Numbers CS031 September 12, 2011 Motivation We’ve seen how unsigned and signed integers are represented by a computer. We’d like to represent decimal numbers like 3.7510 as well. By learning how these numbers are represented in hardware, we can understand and avoid pitfalls of using them in our code. Fixed-Point Binary Representation Fractional numbers are represented in binary much like integers are, but negative exponents and a decimal point are used. 3.7510 = 2+1+0.5+0.25 1 0 -1 -2 = 2 +2 +2 +2 = 11.112 Not all numbers have a finite representation: 0.110 = 0.0625+0.03125+0.0078125+… -4 -5 -8 -9 = 2 +2 +2 +2 +… = 0.00011001100110011… 2 Computer Representation Goals Fixed-point representation assumes no space limitations, so it’s infeasible here. Assume we have 32 bits per number. We want to represent as many decimal numbers as we can, don’t want to sacrifice range. Adding two numbers should be as similar to adding signed integers as possible. Comparing two numbers should be straightforward and intuitive in this representation. The Challenges How many distinct numbers can we represent with 32 bits? Answer: 232 We must decide which numbers to represent. Suppose we want to represent both 3.7510 = 11.112 and 7.510 = 111.12. How will the computer distinguish between them in our representation? Excursus – Scientific Notation 913.8 = 91.38 x 101 = 9.138 x 102 = 0.9138 x 103 We call the final 3 representations scientific notation. It’s standard to use the format 9.138 x 102 (exactly one non-zero digit before the decimal point) for a unique representation. -

Floating Point Numbers and Arithmetic
Overview Floating Point Numbers & • Floating Point Numbers Arithmetic • Motivation: Decimal Scientific Notation – Binary Scientific Notation • Floating Point Representation inside computer (binary) – Greater range, precision • Decimal to Floating Point conversion, and vice versa • Big Idea: Type is not associated with data • MIPS floating point instructions, registers CS 160 Ward 1 CS 160 Ward 2 Review of Numbers Other Numbers •What about other numbers? • Computers are made to deal with –Very large numbers? (seconds/century) numbers 9 3,155,760,00010 (3.1557610 x 10 ) • What can we represent in N bits? –Very small numbers? (atomic diameter) -8 – Unsigned integers: 0.0000000110 (1.010 x 10 ) 0to2N -1 –Rationals (repeating pattern) 2/3 (0.666666666. .) – Signed Integers (Two’s Complement) (N-1) (N-1) –Irrationals -2 to 2 -1 21/2 (1.414213562373. .) –Transcendentals e (2.718...), π (3.141...) •All represented in scientific notation CS 160 Ward 3 CS 160 Ward 4 Scientific Notation Review Scientific Notation for Binary Numbers mantissa exponent Mantissa exponent 23 -1 6.02 x 10 1.0two x 2 decimal point radix (base) “binary point” radix (base) •Computer arithmetic that supports it called •Normalized form: no leadings 0s floating point, because it represents (exactly one digit to left of decimal point) numbers where binary point is not fixed, as it is for integers •Alternatives to representing 1/1,000,000,000 –Declare such variable in C as float –Normalized: 1.0 x 10-9 –Not normalized: 0.1 x 10-8, 10.0 x 10-10 CS 160 Ward 5 CS 160 Ward 6 Floating -

Princeton University COS 217: Introduction to Programming Systems C Primitive Data Types
Princeton University COS 217: Introduction to Programming Systems C Primitive Data Types Type: int Description: A (positive or negative) integer. Size: System dependent. On CourseLab with gcc217: 4 bytes. Example Variable Declarations: int iFirst; signed int iSecond; Example Literals (assuming size is 4 bytes): C Literal Binary Representation Note 123 00000000 00000000 00000000 01111011 decimal form -123 11111111 11111111 11111111 10000101 negative form 0173 00000000 00000000 00000000 01111011 octal form 0x7B 00000000 00000000 00000000 01111011 hexadecimal form 2147483647 01111111 11111111 11111111 11111111 largest -2147483648 10000000 00000000 00000000 00000000 smallest Type: unsigned int Description: A non-negative integer. Size: System dependent. sizeof(unsigned int) == sizeof(int). On CourseLab with gcc217: 4 bytes. Example Variable Declaration: unsigned int uiFirst; unsigned uiSecond; Example Literals (assuming size is 4 bytes): C Literal Binary Representation Note 123U 00000000 00000000 00000000 01111011 decimal form 0173U 00000000 00000000 00000000 01111011 octal form 0x7BU 00000000 00000000 00000000 01111011 hexadecimal form 4294967295U 11111111 11111111 11111111 11111111 largest 0U 00000000 00000000 00000000 00000000 smallest Type: long Description: A (positive or negative) integer. Size: System dependent. sizeof(long) >= sizeof(int). On CourseLab with gcc217: 8 bytes. Example Variable Declarations: long lFirst; long int iSecond; signed long lThird; signed long int lFourth; Page 1 of 5 Example Literals (assuming size is 8 bytes): -
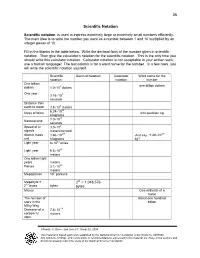
36 Scientific Notation
36 Scientific Notation Scientific notation is used to express extremely large or extremely small numbers efficiently. The main idea is to write the number you want as a number between 1 and 10 multiplied by an integer power of 10. Fill in the blanks in the table below. Write the decimal form of the number given in scientific notation. Then give the calculator’s notation for the scientific notation. This is the only time you should write this calculator notation. Calculator notation is not acceptable in your written work; use a human language! The last column is for a word name for the number. In a few rows, you will write the scientific notation yourself. Scientific Decimal Notation Calculator Word name for the notation notation number One billion one billion dollars dollars 1.0 ×10 9 dollars One year 3.16 ×10 7 seconds Distance from earth to moon 3.8 ×10 8 meters 6.24 ×10 23 Mass of Mars 624 sextillion kg kilograms 1.0 ×10 -9 Nanosecond seconds 8 Speed of tv 3.0 ×10 signals meters/second -27 -27 Atomic mass 1.66 ×10 Just say, “1.66 ×10 unit kilograms kg”! × 12 Light year 6 10 miles 15 Light year 9.5 ×10 meters One billion light years meters 16 Parsec 3.1 ×10 meters 6 Megaparsec 10 parsecs Megabyte = 220 = 1,048,576 20 2 bytes bytes bytes Micron One millionth of a meter The number of About one hundred stars in the billion Milky Way -14 Diameter of a 7.5 ×10 carbon-12 meters atom Rosalie A. -

Floating Point CSE410, Winter 2017
L07: Floating Point CSE410, Winter 2017 Floating Point CSE 410 Winter 2017 Instructor: Teaching Assistants: Justin Hsia Kathryn Chan, Kevin Bi, Ryan Wong, Waylon Huang, Xinyu Sui L07: Floating Point CSE410, Winter 2017 Administrivia Lab 1 due next Thursday (1/26) Homework 2 released today, due 1/31 Lab 0 scores available on Canvas 2 L07: Floating Point CSE410, Winter 2017 Unsigned Multiplication in C u ••• Operands: * bits v ••• True Product: u · v ••• ••• bits Discard bits: UMultw(u , v) ••• bits Standard Multiplication Function . Ignores high order bits Implements Modular Arithmetic w . UMultw(u , v)= u ∙ v mod 2 3 L07: Floating Point CSE410, Winter 2017 Multiplication with shift and add Operation u<<k gives u*2k . Both signed and unsigned u ••• Operands: bits k * 2k 0 ••• 0 1 0 ••• 0 0 True Product: bits u · 2k ••• 0 ••• 0 0 k Discard bits: bits UMultw(u , 2 ) ••• 0 ••• 0 0 k TMultw(u , 2 ) Examples: . u<<3 == u * 8 . u<<5 - u<<3 == u * 24 . Most machines shift and add faster than multiply • Compiler generates this code automatically 4 L07: Floating Point CSE410, Winter 2017 Number Representation Revisited What can we represent in one word? . Signed and Unsigned Integers . Characters (ASCII) . Addresses How do we encode the following: . Real numbers (e.g. 3.14159) . Very large numbers (e.g. 6.02×1023) Floating . Very small numbers (e.g. 6.626×10‐34) Point . Special numbers (e.g. ∞, NaN) 5 L07: Floating Point CSE410, Winter 2017 Floating Point Topics Fractional binary numbers IEEE floating‐point standard Floating‐point operations and rounding Floating‐point in C There are many more details that we won’t cover . -

Fortran Reference Guide
FORTRAN REFERENCE GUIDE Version 2017 TABLE OF CONTENTS Preface............................................................................................................xiv Audience Description.........................................................................................xiv Compatibility and Conformance to Standards........................................................... xiv Organization.................................................................................................... xv Hardware and Software Constraints.......................................................................xvi Conventions.................................................................................................... xvi Related Publications.........................................................................................xvii Chapter 1. Language Overview............................................................................... 1 1.1. Elements of a Fortran Program Unit.................................................................. 1 1.1.1. Fortran Statements................................................................................. 1 1.1.2. Free and Fixed Source............................................................................. 2 1.1.3. Statement Ordering................................................................................. 2 1.2. The Fortran Character Set.............................................................................. 3 1.3. Free Form Formatting.................................................................................. -

The Building Blocks: Data Types, Literals, and Variables
Quigley.book Page 31 Thursday, May 22, 2003 3:19 PM chapter 3 The Building Blocks: Data Types, Literals, and Variables 3.1 Data Types A program can do many things, including calculations, sorting names, preparing phone lists, displaying images, validating forms, ad infinitum. But in order to do anything, the program works with the data that is given to it. Data types specify what kind of data, such as numbers and characters, can be stored and manipulated within a program. Java- Script supports a number of fundamental data types. These types can be broken down into two categories, primitive data types and composite data types. 3.1.1 Primitive Data Types Primitive data types are the simplest building blocks of a program. They are types that can be assigned a single literal value such as the number 5.7, or a string of characters such as "hello". JavaScript supports three core or basic data types: • numeric • string • Boolean In addition to the three core data types, there are two other special types that consist of a single value: • null • undefined Numeric Literals. JavaScript supports both integers and floating-point numbers. Integers are whole numbers and do not contain a decimal point; e.g., 123 and –6. Inte- gers can be expressed in decimal (base 10), octal (base 8), and hexadecimal (base 16), and are either positive or negative values. See Example 3.1. 31 Quigley.book Page 32 Thursday, May 22, 2003 3:19 PM 32 Chapter 3 • The Building Blocks: Data Types, Literals, and Variables Floating-point numbers are fractional numbers such as 123.56 or –2.5. -

Scientific Notation TEACHER NOTES
Scientific Notation TEACHER NOTES Activity Overview This activity gives students an opportunity to see where large and small numbers are used and how scientific notation offers a convenient method of writing such numbers. Topic: Numbers and Operations Understand numbers, ways of representing numbers, relationships among numbers, and number systems Develop an understanding of large numbers and recognize and This activity utilizes MathPrintTM appropriately use exponential, scientific, and calculator notation functionality and includes screen captures taken from the TI-84 Teacher Preparation and Notes Plus C Silver Edition. It is also To download the data list and student worksheet, go to appropriate for use with the TI-83 education.ti.com/exchange/sn Plus, TI-84 Plus, and TI-84 Plus Silver Edition but slight variances may be found within the directions. Compatible Devices: TI-84 Plus Family TI-84 Plus C Silver Edition Associated Materials: Scientific_Notation_Student.pdf Scientific_Notation_Student.doc Tech Tips: Access free tutorials at http://education.ti.com/calculators /pd/US/Online-Learning/Tutorials Any required calculator files can be distributed to students via handheld-to-handheld transfer. ©2013 Texas Instruments Incorporated 1 education.ti.com Scientific Notation TEACHER NOTES Part 1 – Writing Scientific Notation in Expanded Form Questions 1 -4 Have students write their answers and check them on the calculator. Help students understand the form for scientific notation. Students can enter scientific notation numbers two different ways, using 10 or E. Note that the key is labeled EE but the display is E. 1. _ 3 . 7 7 * 1 0 ^ 8 2. _ 3 . 7 7 `£ 8 To check –3.77108, enter in one of the two ways shown above and see if it matches their answer. -

Floating-Point Arithmetic
Floating-Point Arithmetic if ((A + A) - A == A) { SelfDestruct() } Reading: Study Chapter 3. Comp 411 – Spring 2013 03/04/2013 L11 – Floating Point 1 Why Floating Point? Aren’t Integers enough? • Many applications require numbers with a VERY large range. (e.g. nanoseconds to centuries) • Most scientific applications need real numbers (e.g. π) But so far we have only used integers. • We *COULD* use integers with a fixed “binary” point • We *COULD* implement rational fractions using two integers (e.g. ½, 1023/102934) • Floating point is a better answer for most applications. Comp 411 – Spring 2013 03/04/2013 L11 – Floating Point 2 Recall Scientific Notation • Let’s start our discussion of floating point by recalling scientific notation from high school Significant Digits • Numbers represented in parts: Exponent 42 = 4.200 x 101 1024 = 1.024 x 103 -0.0625 = -6.250 x 10-2 • Arithmetic is done in pieces 3 Before adding, we must match the 1024 1.024 x 10 exponents, effectively “denormalizing” the smaller magnitude number - 42 - 0.042 x 103 982 0.982 x 103 2 9.820 x 10 We then “normalize” the final result so there is one digit to the left of the decimal point and adjust the exponent accordingly. Comp 411 – Spring 2013 03/04/2013 L11 – Floating Point 3 Multiplication in Scientific Notation • Is straightforward: – Multiply together the significant parts – Add the exponents In multiplication, how far is the most you will – Normalize if required ever normalize? • Examples: 1024 1.024 x 103 In addition? x 0.0625 6.250 x 10-2 64 6.400 x 101 42 4.200