DOCSLIB.ORG

Fortran Reference Guide

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fortran Reference Guide FORTRAN REFERENCE GUIDE Version 2017 TABLE OF CONTENTS Preface............................................................................................................xiv Audience Description.........................................................................................xiv Compatibility and Conformance to Standards........................................................... xiv Organization.................................................................................................... xv Hardware and Software Constraints.......................................................................xvi Conventions.................................................................................................... xvi Related Publications.........................................................................................xvii Chapter 1. Language Overview............................................................................... 1 1.1. Elements of a Fortran Program Unit.................................................................. 1 1.1.1. Fortran Statements................................................................................. 1 1.1.2. Free and Fixed Source............................................................................. 2 1.1.3. Statement Ordering................................................................................. 2 1.2. The Fortran Character Set.............................................................................. 3 1.3. Free Form Formatting................................................................................... 4 1.4. Fixed Formatting..........................................................................................5 1.4.1. Column Formatting..................................................................................5 1.4.2. Fixed Format Label Field.......................................................................... 5 1.4.3. Fixed Format Continuation Field................................................................. 5 1.4.4. Fixed Format Statement Field.................................................................... 6 1.4.5. Fixed Format Debug Statements..................................................................6 1.4.6. Tab Formatting.......................................................................................6 1.4.7. Fixed Input File Format Summary................................................................ 6 1.5. Include Fortran Source Files............................................................................ 7 1.6. Components of Fortran Statements................................................................... 7 1.6.1. Symbolic Names..................................................................................... 8 1.7. Expressions.................................................................................................8 1.7.1. Forming Expressions.................................................................................8 1.7.2. Expression Precedence Rules...................................................................... 9 1.7.3. Arithmetic Expressions............................................................................. 9 1.7.4. Relational Expressions.............................................................................11 1.7.5. Logical Expressions................................................................................ 12 1.7.6. Character Expressions............................................................................. 12 1.7.7. Character Concatenation......................................................................... 12 1.8. Symbolic Name Scope.................................................................................. 13 1.9. Assignment Statements.................................................................................13 1.9.1. Arithmetic Assignment............................................................................ 13 1.9.2. Logical Assignment.................................................................................14 1.9.3. Character Assignment............................................................................. 14 1.10. Listing Controls.........................................................................................15 1.11. OpenMP Directives..................................................................................... 15 Fortran Reference Guide Version 2017 | ii Chapter 2. Fortran Data Types.............................................................................. 16 2.1. Intrinsic Data Types..................................................................................... 16 2.1.1. Kind Parameter..................................................................................... 16 2.1.2. Number of Bytes Specification.................................................................. 17 2.2. Constants................................................................................................. 19 2.2.1. Integer Constants.................................................................................. 19 2.2.2. Binary, Octal and Hexadecimal Constants..................................................... 20 2.2.3. Real Constants......................................................................................20 2.2.4. Double Precision Constants.......................................................................21 2.2.5. Complex Constants................................................................................ 21 2.2.6. Double Complex Constants....................................................................... 21 2.2.7. Logical Constants.................................................................................. 21 2.2.8. Character Constants............................................................................... 22 2.2.9. Parameter Constants.............................................................................. 22 2.3. Structure Constructors................................................................................. 23 2.4. Derived Types............................................................................................ 24 2.5. Deferred Type Parameters............................................................................. 25 2.5.1. Typed Allocation................................................................................... 25 2.6. Arrays......................................................................................................26 2.6.1. Array Declaration Element....................................................................... 26 2.6.2. Deferred Shape Arrays............................................................................ 27 2.6.3. Subscripts............................................................................................27 2.6.4. Character Substring................................................................................27 2.6.5. Array Constructor Syntax......................................................................... 28 2.7. Fortran Pointers and Targets.......................................................................... 28 2.8. Fortran Binary, Octal and Hexadecimal Constants.................................................28 2.8.1. Octal and Hexadecimal Constants - Alternate Forms........................................ 29 2.9. Hollerith Constants......................................................................................30 2.10. Structures............................................................................................... 31 2.10.1. Records............................................................................................. 32 2.10.2. UNION and MAP Declarations................................................................... 33 2.10.3. Data Initialization................................................................................ 35 2.11. Pointer Variables....................................................................................... 35 2.11.1. Restrictions........................................................................................ 36 2.11.2. Pointer Assignment............................................................................... 37 Chapter 3. Fortran Statements.............................................................................. 38 3.1. Statement Format Overview.......................................................................... 38 3.1.1. Definition of Statement-related Terms.........................................................38 3.1.2. Origin of Statement............................................................................... 39 3.1.3. List-related Notation.............................................................................. 39 3.2. Fortran Statement Summary Table................................................................... 39 3.3. ACCEPT.................................................................................................... 44 3.4. ARRAY......................................................................................................45 Fortran Reference Guide Version 2017 | iii 3.5. BYTE....................................................................................................... 46 3.6. DECODE....................................................................................................47 3.7. DOUBLE COMPLEX....................................................................................... 48 3.8. DOUBLE
Load more

Recommended publications
  • TI 83/84: Scientific Notation on Your Calculator
    TI 83/84: Scientific Notation on your calculator this is above the comma, next to the square root! choose the proper MODE : Normal or Sci entering numbers: 2.39 x 106 on calculator: 2.39 2nd EE 6 ENTER reading numbers: 2.39E6 on the calculator means for us. • When you're in Normal mode, the calculator will write regular numbers unless they get too big or too small, when it will switch to scientific notation. • In Sci mode, the calculator displays every answer as scientific notation. • In both modes, you can type in numbers in scientific notation or as regular numbers. Humans should never, ever, ever write scientific notation using the calculator’s E notation! Try these problems. Answer in scientific notation, and round decimals to two places. 2.39 x 1016 (5) 2.39 x 109+ 4.7 x 10 10 (4) 4.7 x 10−3 3.01 103 1.07 10 0 2.39 10 5 4.94 10 10 5.09 1018 − 3.76 10−− 1 2.39 10 5 7.93 10 8 Remember to change your MODE back to Normal when you're done. Using the STORE key: Let's say that you want to store a number so that you can use it later, or that you want to store answers for several different variables, and then use them together in one problem. Here's how: Enter the number, then press STO (above the ON key), then press ALPHA and the letter you want. (The letters are in alphabetical order above the other keys.) Then press ENTER.
    [Show full text]
  • Primitive Number Types
    Primitive number types Values of each of the primitive number types Java has these 4 primitive integral types: byte: A value occupies 1 byte (8 bits). The range of values is -2^7..2^7-1, or -128..127 short: A value occupies 2 bytes (16 bits). The range of values is -2^15..2^15-1 int: A value occupies 4 bytes (32 bits). The range of values is -2^31..2^31-1 long: A value occupies 8 bytes (64 bits). The range of values is -2^63..2^63-1 and two “floating-point” types, whose values are approximations to the real numbers: float: A value occupies 4 bytes (32 bits). double: A value occupies 8 bytes (64 bits). Values of the integral types are maintained in two’s complement notation (see the dictionary entry for two’s complement notation). A discussion of floating-point values is outside the scope of this website, except to say that some bits are used for the mantissa and some for the exponent and that infinity and NaN (not a number) are both floating-point values. We don’t discuss this further. Generally, one uses mainly types int and double. But if you are declaring a large array and you know that the values fit in a byte, you can save ¾ of the space using a byte array instead of an int array, e.g. byte[] b= new byte[1000]; Operations on the primitive integer types Types byte and short have no operations. Instead, operations on their values int and long operations are treated as if the values were of type int.
    [Show full text]
  • The Machine That Builds Itself: How the Strengths of Lisp Family
    Khomtchouk et al. OPINION NOTE The Machine that Builds Itself: How the Strengths of Lisp Family Languages Facilitate Building Complex and Flexible Bioinformatic Models Bohdan B. Khomtchouk1*, Edmund Weitz2 and Claes Wahlestedt1 *Correspondence: [email protected] Abstract 1Center for Therapeutic Innovation and Department of We address the need for expanding the presence of the Lisp family of Psychiatry and Behavioral programming languages in bioinformatics and computational biology research. Sciences, University of Miami Languages of this family, like Common Lisp, Scheme, or Clojure, facilitate the Miller School of Medicine, 1120 NW 14th ST, Miami, FL, USA creation of powerful and flexible software models that are required for complex 33136 and rapidly evolving domains like biology. We will point out several important key Full list of author information is features that distinguish languages of the Lisp family from other programming available at the end of the article languages and we will explain how these features can aid researchers in becoming more productive and creating better code. We will also show how these features make these languages ideal tools for artificial intelligence and machine learning applications. We will specifically stress the advantages of domain-specific languages (DSL): languages which are specialized to a particular area and thus not only facilitate easier research problem formulation, but also aid in the establishment of standards and best programming practices as applied to the specific research field at hand. DSLs are particularly easy to build in Common Lisp, the most comprehensive Lisp dialect, which is commonly referred to as the “programmable programming language.” We are convinced that Lisp grants programmers unprecedented power to build increasingly sophisticated artificial intelligence systems that may ultimately transform machine learning and AI research in bioinformatics and computational biology.
    [Show full text]
  • INTRODUCTION to PL/1 PL/I Is a Structured Language to Develop Systems and Applications Programs (Both Business and Scientific)
    INTRODUCTION TO PL/1 PL/I is a structured language to develop systems and applications programs (both business and scientific). Significant features : v Allows Free format v Regards a program as a continuous stream of data v Supports subprogram and functions v Uses defaults 1 Created by Sanjay Sinha Building blocks of PL/I : v Made up of a series of subprograms and called Procedure v Program is structured into a MAIN program and subprograms. v Subprograms include subroutine and functions. Every PL/I program consists of : v At least one Procedure v Blocks v Group 2 Created by Sanjay Sinha v There must be one and only one MAIN procedure to every program, the MAIN procedure statement consists of : v Label v The statement ‘PROCEDURE OPTIONS (MAIN)’ v A semicolon to mark the end of the statement. Coding a Program : 1. Comment line(s) begins with /* and ends with */. Although comments may be embedded within a PL/I statements , but it is recommended to keep the embedded comments minimum. 3 Created by Sanjay Sinha 2. The first PL/I statement in the program is the PROCEDURE statement : AVERAGE : PROC[EDURE] OPTIONS(MAIN); AVERAGE -- it is the name of the program(label) and compulsory and marks the beginning of a program. OPTIONS(MAIN) -- compulsory for main programs and if not specified , then the program is a subroutine. A PL/I program is compiled by PL/I compiler and converted into the binary , Object program file for link editing . 4 Created by Sanjay Sinha Advantages of PL/I are : 1. Better integration of sets of programs covering several applications.
    [Show full text]
  • C++ Data Types
    Software Design & Programming I Starting Out with C++ (From Control Structures through Objects) 7th Edition Written by: Tony Gaddis Pearson - Addison Wesley ISBN: 13-978-0-132-57625-3 Chapter 2 (Part II) Introduction to C++ The char Data Type (Sample Program) Character and String Constants The char Data Type Program 2-12 assigns character constants to the variable letter. Anytime a program works with a character, it internally works with the code used to represent that character, so this program is still assigning the values 65 and 66 to letter. Character constants can only hold a single character. To store a series of characters in a constant we need a string constant. In the following example, 'H' is a character constant and "Hello" is a string constant. Notice that a character constant is enclosed in single quotation marks whereas a string constant is enclosed in double quotation marks. cout << ‘H’ << endl; cout << “Hello” << endl; The char Data Type Strings, which allow a series of characters to be stored in consecutive memory locations, can be virtually any length. This means that there must be some way for the program to know how long the string is. In C++ this is done by appending an extra byte to the end of string constants. In this last byte, the number 0 is stored. It is called the null terminator or null character and marks the end of the string. Don’t confuse the null terminator with the character '0'. If you look at Appendix A you will see that the character '0' has ASCII code 48, whereas the null terminator has ASCII code 0.
    [Show full text]
  • A Block Design for Introductory Functional Programming in Haskell
    A Block Design for Introductory Functional Programming in Haskell Matthew Poole School of Computing University of Portsmouth, UK [email protected] Abstract—This paper describes the visual design of blocks for the learner, and to avoid syntax and type-based errors entirely editing code in the functional language Haskell. The aim of the through blocks-based program construction. proposed blocks-based environment is to support students’ initial steps in learning functional programming. Expression blocks and There exists some recent work in representing functional slots are shaped to ensure constructed code is both syntactically types within blocks-based environments. TypeBlocks [9] in- correct and preserves conventional use of whitespace. The design cludes three basic type connector shapes (for lists, tuples aims to help students learn Haskell’s sophisticated type system and functions) which can be combined in any way and to which is often regarded as challenging for novice functional any depth. The prototype blocks editor for Bootstrap [10], programmers. Types are represented using text, color and shape, [11] represents each of the five types of a simple functional and empty slots indicate valid argument types in order to ensure language using a different color, with a neutral color (gray) that constructed code is well-typed. used for polymorphic blocks; gray blocks change color once their type has been determined during program construction. I. INTRODUCTION Some functional features have also been added to Snap! [12] Blocks-based environments such as Scratch [1] and Snap! and to a modified version of App Inventor [13]. [2] offer several advantages over traditional text-based lan- This paper is structured as follows.
    [Show full text]
  • Floating Point Numbers
    Floating Point Numbers CS031 September 12, 2011 Motivation We’ve seen how unsigned and signed integers are represented by a computer. We’d like to represent decimal numbers like 3.7510 as well. By learning how these numbers are represented in hardware, we can understand and avoid pitfalls of using them in our code. Fixed-Point Binary Representation Fractional numbers are represented in binary much like integers are, but negative exponents and a decimal point are used. 3.7510 = 2+1+0.5+0.25 1 0 -1 -2 = 2 +2 +2 +2 = 11.112 Not all numbers have a finite representation: 0.110 = 0.0625+0.03125+0.0078125+… -4 -5 -8 -9 = 2 +2 +2 +2 +… = 0.00011001100110011… 2 Computer Representation Goals Fixed-point representation assumes no space limitations, so it’s infeasible here. Assume we have 32 bits per number. We want to represent as many decimal numbers as we can, don’t want to sacrifice range. Adding two numbers should be as similar to adding signed integers as possible. Comparing two numbers should be straightforward and intuitive in this representation. The Challenges How many distinct numbers can we represent with 32 bits? Answer: 232 We must decide which numbers to represent. Suppose we want to represent both 3.7510 = 11.112 and 7.510 = 111.12. How will the computer distinguish between them in our representation? Excursus – Scientific Notation 913.8 = 91.38 x 101 = 9.138 x 102 = 0.9138 x 103 We call the final 3 representations scientific notation. It’s standard to use the format 9.138 x 102 (exactly one non-zero digit before the decimal point) for a unique representation.
    [Show full text]
  • Floating Point Numbers and Arithmetic
    Overview Floating Point Numbers & • Floating Point Numbers Arithmetic • Motivation: Decimal Scientific Notation – Binary Scientific Notation • Floating Point Representation inside computer (binary) – Greater range, precision • Decimal to Floating Point conversion, and vice versa • Big Idea: Type is not associated with data • MIPS floating point instructions, registers CS 160 Ward 1 CS 160 Ward 2 Review of Numbers Other Numbers •What about other numbers? • Computers are made to deal with –Very large numbers? (seconds/century) numbers 9 3,155,760,00010 (3.1557610 x 10 ) • What can we represent in N bits? –Very small numbers? (atomic diameter) -8 – Unsigned integers: 0.0000000110 (1.010 x 10 ) 0to2N -1 –Rationals (repeating pattern) 2/3 (0.666666666. .) – Signed Integers (Two’s Complement) (N-1) (N-1) –Irrationals -2 to 2 -1 21/2 (1.414213562373. .) –Transcendentals e (2.718...), π (3.141...) •All represented in scientific notation CS 160 Ward 3 CS 160 Ward 4 Scientific Notation Review Scientific Notation for Binary Numbers mantissa exponent Mantissa exponent 23 -1 6.02 x 10 1.0two x 2 decimal point radix (base) “binary point” radix (base) •Computer arithmetic that supports it called •Normalized form: no leadings 0s floating point, because it represents (exactly one digit to left of decimal point) numbers where binary point is not fixed, as it is for integers •Alternatives to representing 1/1,000,000,000 –Declare such variable in C as float –Normalized: 1.0 x 10-9 –Not normalized: 0.1 x 10-8, 10.0 x 10-10 CS 160 Ward 5 CS 160 Ward 6 Floating
    [Show full text]
  • Kednos PL/I for Openvms Systems User Manual
    ) Kednos PL/I for OpenVMS Systems User Manual Order Number: AA-H951E-TM November 2003 This manual provides an overview of the PL/I programming language. It explains programming with Kednos PL/I on OpenVMS VAX Systems and OpenVMS Alpha Systems. It also describes the operation of the Kednos PL/I compilers and the features of the operating systems that are important to the PL/I programmer. Revision/Update Information: This revised manual supersedes the PL/I User’s Manual for VAX VMS, Order Number AA-H951D-TL. Operating System and Version: For Kednos PL/I for OpenVMS VAX: OpenVMS VAX Version 5.5 or higher For Kednos PL/I for OpenVMS Alpha: OpenVMS Alpha Version 6.2 or higher Software Version: Kednos PL/I Version 3.8 for OpenVMS VAX Kednos PL/I Version 4.4 for OpenVMS Alpha Published by: Kednos Corporation, Pebble Beach, CA, www.Kednos.com First Printing, August 1980 Revised, November 1983 Updated, April 1985 Revised, April 1987 Revised, January 1992 Revised, May 1992 Revised, November 1993 Revised, April 1995 Revised, October 1995 Revised, November 2003 Kednos Corporation makes no representations that the use of its products in the manner described in this publication will not infringe on existing or future patent rights, nor do the descriptions contained in this publication imply the granting of licenses to make, use, or sell equipment or software in accordance with the description. Possession, use, or copying of the software described in this publication is authorized only pursuant to a valid written license from Kednos Corporation or an anthorized sublicensor.
    [Show full text]
  • Princeton University COS 217: Introduction to Programming Systems C Primitive Data Types
    Princeton University COS 217: Introduction to Programming Systems C Primitive Data Types Type: int Description: A (positive or negative) integer. Size: System dependent. On CourseLab with gcc217: 4 bytes. Example Variable Declarations: int iFirst; signed int iSecond; Example Literals (assuming size is 4 bytes): C Literal Binary Representation Note 123 00000000 00000000 00000000 01111011 decimal form -123 11111111 11111111 11111111 10000101 negative form 0173 00000000 00000000 00000000 01111011 octal form 0x7B 00000000 00000000 00000000 01111011 hexadecimal form 2147483647 01111111 11111111 11111111 11111111 largest -2147483648 10000000 00000000 00000000 00000000 smallest Type: unsigned int Description: A non-negative integer. Size: System dependent. sizeof(unsigned int) == sizeof(int). On CourseLab with gcc217: 4 bytes. Example Variable Declaration: unsigned int uiFirst; unsigned uiSecond; Example Literals (assuming size is 4 bytes): C Literal Binary Representation Note 123U 00000000 00000000 00000000 01111011 decimal form 0173U 00000000 00000000 00000000 01111011 octal form 0x7BU 00000000 00000000 00000000 01111011 hexadecimal form 4294967295U 11111111 11111111 11111111 11111111 largest 0U 00000000 00000000 00000000 00000000 smallest Type: long Description: A (positive or negative) integer. Size: System dependent. sizeof(long) >= sizeof(int). On CourseLab with gcc217: 8 bytes. Example Variable Declarations: long lFirst; long int iSecond; signed long lThird; signed long int lFourth; Page 1 of 5 Example Literals (assuming size is 8 bytes):
    [Show full text]
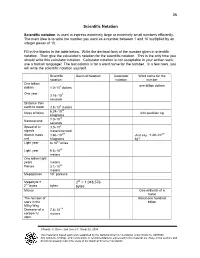
  • 36 Scientific Notation
    36 Scientific Notation Scientific notation is used to express extremely large or extremely small numbers efficiently. The main idea is to write the number you want as a number between 1 and 10 multiplied by an integer power of 10. Fill in the blanks in the table below. Write the decimal form of the number given in scientific notation. Then give the calculator’s notation for the scientific notation. This is the only time you should write this calculator notation. Calculator notation is not acceptable in your written work; use a human language! The last column is for a word name for the number. In a few rows, you will write the scientific notation yourself. Scientific Decimal Notation Calculator Word name for the notation notation number One billion one billion dollars dollars 1.0 ×10 9 dollars One year 3.16 ×10 7 seconds Distance from earth to moon 3.8 ×10 8 meters 6.24 ×10 23 Mass of Mars 624 sextillion kg kilograms 1.0 ×10 -9 Nanosecond seconds 8 Speed of tv 3.0 ×10 signals meters/second -27 -27 Atomic mass 1.66 ×10 Just say, “1.66 ×10 unit kilograms kg”! × 12 Light year 6 10 miles 15 Light year 9.5 ×10 meters One billion light years meters 16 Parsec 3.1 ×10 meters 6 Megaparsec 10 parsecs Megabyte = 220 = 1,048,576 20 2 bytes bytes bytes Micron One millionth of a meter The number of About one hundred stars in the billion Milky Way -14 Diameter of a 7.5 ×10 carbon-12 meters atom Rosalie A.
    [Show full text]
  • E.W. Dijkstra Archive: on the Cruelty of Really Teaching Computing Science
    On the cruelty of really teaching computing science Edsger W. Dijkstra. (EWD1036) http://www.cs.utexas.edu/users/EWD/ewd10xx/EWD1036.PDF The second part of this talk pursues some of the scientific and educational consequences of the assumption that computers represent a radical novelty. In order to give this assumption clear contents, we have to be much more precise as to what we mean in this context by the adjective "radical". We shall do so in the first part of this talk, in which we shall furthermore supply evidence in support of our assumption. The usual way in which we plan today for tomorrow is in yesterday’s vocabulary. We do so, because we try to get away with the concepts we are familiar with and that have acquired their meanings in our past experience. Of course, the words and the concepts don’t quite fit because our future differs from our past, but then we stretch them a little bit. Linguists are quite familiar with the phenomenon that the meanings of words evolve over time, but also know that this is a slow and gradual process. It is the most common way of trying to cope with novelty: by means of metaphors and analogies we try to link the new to the old, the novel to the familiar. Under sufficiently slow and gradual change, it works reasonably well; in the case of a sharp discontinuity, however, the method breaks down: though we may glorify it with the name "common sense", our past experience is no longer relevant, the analogies become too shallow, and the metaphors become more misleading than illuminating.
    [Show full text]