DOCSLIB.ORG

Floating Point Numbers and Arithmetic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Floating Point Numbers and Arithmetic Overview Floating Point Numbers & • Floating Point Numbers Arithmetic • Motivation: Decimal Scientific Notation – Binary Scientific Notation • Floating Point Representation inside computer (binary) – Greater range, precision • Decimal to Floating Point conversion, and vice versa • Big Idea: Type is not associated with data • MIPS floating point instructions, registers CS 160 Ward 1 CS 160 Ward 2 Review of Numbers Other Numbers •What about other numbers? • Computers are made to deal with –Very large numbers? (seconds/century) numbers 9 3,155,760,00010 (3.1557610 x 10 ) • What can we represent in N bits? –Very small numbers? (atomic diameter) -8 – Unsigned integers: 0.0000000110 (1.010 x 10 ) 0to2N -1 –Rationals (repeating pattern) 2/3 (0.666666666. .) – Signed Integers (Two’s Complement) (N-1) (N-1) –Irrationals -2 to 2 -1 21/2 (1.414213562373. .) –Transcendentals e (2.718...), π (3.141...) •All represented in scientific notation CS 160 Ward 3 CS 160 Ward 4 Scientific Notation Review Scientific Notation for Binary Numbers mantissa exponent Mantissa exponent 23 -1 6.02 x 10 1.0two x 2 decimal point radix (base) “binary point” radix (base) •Computer arithmetic that supports it called •Normalized form: no leadings 0s floating point, because it represents (exactly one digit to left of decimal point) numbers where binary point is not fixed, as it is for integers •Alternatives to representing 1/1,000,000,000 –Declare such variable in C as float –Normalized: 1.0 x 10-9 –Not normalized: 0.1 x 10-8, 10.0 x 10-10 CS 160 Ward 5 CS 160 Ward 6 Floating Point Representation [1] Floating Point Representation [2] yyyy 38 • Normal format: +1.xxxxxxxxxxtwo*2 two • What if result too large? (> 2.0x10 ) • Multiple of Word Size (32 bits) – Overflow! – Overflow => Exponent larger than 31 30 23 22 0 represented in 8-bit Exponent field S Exponent Significand • What if result too small? (>0, < 2.0x10-38 ) 1 bit 8 bits 23 bits – Underflow! • S represents Sign of significand (number) – Underflow => Negative exponent larger than Exponent represents y’s represented in 8-bit Exponent field Significand represents x’s • How to reduce chances of overflow or underflow? • Represent numbers as small as 2.0 x 10-38 to as large as 2.0 x 1038 CS 160 Ward 7 CS 160 Ward 8 Double Precision Fl. Pt. IEEE 754 Fl. Pt. Standard [1] • Next Multiple of Word Size (64 bits) • Single Precision, DP similar 31 30 20 19 0 • Sign bit: 1 means negative S Exponent Significand 0 means positive 1 bit 11 bits 20 bits Significand (cont’d) • Significand: 32 bits – To pack more bits, leading 1 implicit for • Double Precision (vs. Single Precision) normalized numbers – 1 + 23 bits single, 1 + 52 bits double – C variable declared as double – always true: 0 < Significand < 1 – Represent numbers almost as small as 2.0 x 10-308 to almost as large as 2.0 x 10308 • Note: 0 has no leading 1, so reserve – But primary advantage is greater accuracy exponent value 0 just for number 0 due to larger significand CS 160 Ward 9 CS 160 Ward 10 IEEE 754 Fl. Pt. Standard [2] IEEE 754 Fl. Pt. Standard [3] •Negative Exponent? •Called Biased Notation, where bias is number –2’s comp? 1.0 x 2-1 v. 1.0 x2+1 (1/2 v. 2) subtract to get real number –IEEE 754 uses bias of 127 for single precision 1/2 0 1111 1111 000 0000 0000 0000 0000 0000 –Subtract 127 from Exponent field to get actual value for 2 0 0000 0001 000 0000 0000 0000 0000 0000 exponent –1023 is bias for double precision –This notation using integer compare of 1/2 v. 2 makes 1/2 > 2! • Summary (single precision): •Instead, pick notation 0000 0001 is most 3130 2322 0 negative, and 1111 1111 is most positive S Exponent Significand –1.0 x 2-1 v. 1.0 x2+1 (1/2 v. 2) 1 bit 8 bits 23 bits 1/2 0 0111 1110 000 0000 0000 0000 0000 0000 • (-1)S x (1 + Significand) x 2(Exponent-127) 2 0 1000 0000 000 0000 0000 0000 0000 0000 – Double precision identical, except with exponent bias of 1023 and significand of 52 bits CS 160 Ward 11 CS 160 Ward 12 Understanding the Significand [1] Understanding the Significand [2] • Method 1 (Fractions): • Method 2 (Place Values): – Convert from scientific notation – In decimal: 0.34010 => 34010/100010 0 -1 => 3410/10010 – In decimal: 1.6732 = (1x10 ) + (6x10 ) + (7x10-2) + (3x10-3) + (2x10-4) – In binary: 0.110 => 110 /1000 = 6 /8 2 2 2 10 10 0 -1 -2 => 11 /100 = 3 /4 – In binary: 1.1001 = (1x2 ) + (1x2 ) + (0x2 ) 2 2 10 10 + (0x2-3) + (1x2-4) – Advantage: less purely numerical, more thought – Interpretation of value in each position extends oriented; this method usually helps people beyond the decimal/binary point understand the meaning of the significand better – Advantage: good for quickly calculating significand value; use this method for translating FP numbers CS 160 Ward 13 CS 160 Ward 14 Ex: Converting Binary FP to Decimal Continuing Example: Binary to ??? 0 0110 1000 101 0101 0100 0011 0100 0010 0011 0100 0101 0101 0100 0011 0100 0010 • Convert 2’s Comp. Binary to Integer: • Sign: 0 => positive 229+228+226+222+220+218+216+214+29+28+26+ 21 • Exponent: = 878,003,010ten – 0110 1000two = 104ten • Convert Binary to Instruction: – Bias adjustment: 104 - 127 = -23 0011 0100 0101 0101 0100 0011 0100 0010 • Significand: 13 221 17218 – 1 + 1x2-1+ 0x2-2 + 1x2-3 + 0x2-4 + 1x2-5 +... =1+2-1+2-3 +2-5 +2-7 +2-9 +2-14 +2-15 +2-17 +2-22 ori $s5, $v0, 17218 = 1.0 + 0.666115 • Convert Binary to ASCII: -23 -7 • Represents: 1.666115ten*2 ~ 1.986*10 0011 0100 0101 0101 0100 0011 0100 0010 (about 2/10,000,000) 4UCB CS 160 Ward 15 CS 160 Ward 16 Big Idea: Type not associated with Data Converting Decimal to FP [1] 0011 0100 0101 0101 0100 0011 0100 0010 • Simple Case: If denominator is an exponent of •What does bit pattern mean: 2 (2, 4, 8, 16, etc.), then it’s easy. –1.986 *10-7? 878,003,010? “4UCB”? • Show IEEE 32-bit representation of -0.75 ori $s5, $v0, 17218? – -0.75 = -3/4 •Data can be anything; operation of instruction that accesses operand determines its type! – -11two/100two = -0.11two -1 –Side-effect of stored program concept: – Normalized to -1.1two x 2 instructions stored as numbers – (-1)S x (1 + Significand) x 2(Exponent-127) •Power/danger of unrestricted addresses/ pointers: use ASCII as Fl. Pt., instructions as data, integers – (-1)1 x (1 + .100 0000 ... 0000) x 2(126-127) as instructions, ... 1 0111 1110 100 0000 0000 0000 0000 0000 CS 160 Ward 17 CS 160 Ward 18 Converting Decimal to FP [2] Converting Decimal to FP [3] • Not So Simple Case: If denominator is not an • Fact: All rational numbers have a exponent of 2. repeating pattern when written out in – Then we can’t represent number precisely, but that’s decimal. why we have so many bits in significand: for • Fact: This still applies in binary. precision – Once we have significand, normalizing a number to • To finish conversion: get the exponent is easy. – Write out binary number with repeating – So how do we get the significand of a neverending pattern. number? – Cut it off after correct number of bits (different for single vs. double precision). – Derive Sign, Exponent and Significand fields. CS 160 Ward 19 CS 160 Ward 20 Hairy Example [1] Hairy Example [2] • How to represent 1/3 in IEEE 32-bit? • Sign: 0 • 1/3 • Exponent = -2 + 127 = 125 =01111101 = 0.33333…10 10 2 = 0.25 + 0.0625 + 0.015625 + 0.00390625 • Significand = 0101010101… + 0.0009765625 + … 0 0111 1101 0101 0101 0101 0101 0101 010 = 1/4 + 1/16 + 1/64 + 1/256 + 1/1024 + … = 2-2 + 2-4 + 2-6 + 2-8 + 2-10 + … 0 = 0.0101010101… 2 * 2 -2 = 1.0101010101… 2 * 2 CS 160 Ward 21 CS 160 Ward 22 Representation for +/- Infinity Representation for 0 • In FP, divide by zero should produce +/- • Represent 0? infinity, not overflow. – exponent all zeroes • Why? – significand all zeroes too – OK to do further computations with infinity – What about sign? e.g., X/0 > Y may be a valid comparison – +0: 0 00000000 00000000000000000000000 • IEEE 754 represents +/- infinity – -0: 1 00000000 00000000000000000000000 • Why two zeroes? – Most positive exponent reserved for infinity – Helps in some limit comparisons – Significands all zeroes CS 160 Ward 23 CS 160 Ward 24 Special Numbers FP Addition • What have we defined so far? • Much more difficult than with integers (Single Precision) • Can’t just add significands Exponent Significand Object • How do we do it? 00 0 – De-normalize to match exponents 0 nonzero Denormalized – Add significands to get resulting significand 1-254 anything +/- fl. pt. # – Keep the same exponent 255 0 +/- infinity – Normalize (possibly changing exponent) 255 nonzero ??? • Note: If signs differ, just perform a subtract instead. CS 160 Ward 25 CS 160 Ward 26 FP Subtraction FP Addition/Subtraction • Similar to addition • Problems in implementing FP add/sub: • How do we do it? – If signs differ for add (or same for sub), what will be the sign of the result? – De-normalize to match exponents – Subtract significands • Question: How do we integrate this into the integer arithmetic unit? – Keep the same exponent – Normalize (possibly changing exponent) • Answer: We don’t! CS 160 Ward 27 CS 160 Ward 28 Fl.
Load more

Recommended publications
  • TI 83/84: Scientific Notation on Your Calculator
    TI 83/84: Scientific Notation on your calculator this is above the comma, next to the square root! choose the proper MODE : Normal or Sci entering numbers: 2.39 x 106 on calculator: 2.39 2nd EE 6 ENTER reading numbers: 2.39E6 on the calculator means for us. • When you're in Normal mode, the calculator will write regular numbers unless they get too big or too small, when it will switch to scientific notation. • In Sci mode, the calculator displays every answer as scientific notation. • In both modes, you can type in numbers in scientific notation or as regular numbers. Humans should never, ever, ever write scientific notation using the calculator’s E notation! Try these problems. Answer in scientific notation, and round decimals to two places. 2.39 x 1016 (5) 2.39 x 109+ 4.7 x 10 10 (4) 4.7 x 10−3 3.01 103 1.07 10 0 2.39 10 5 4.94 10 10 5.09 1018 − 3.76 10−− 1 2.39 10 5 7.93 10 8 Remember to change your MODE back to Normal when you're done. Using the STORE key: Let's say that you want to store a number so that you can use it later, or that you want to store answers for several different variables, and then use them together in one problem. Here's how: Enter the number, then press STO (above the ON key), then press ALPHA and the letter you want. (The letters are in alphabetical order above the other keys.) Then press ENTER.
    [Show full text]
  • Primitive Number Types
    Primitive number types Values of each of the primitive number types Java has these 4 primitive integral types: byte: A value occupies 1 byte (8 bits). The range of values is -2^7..2^7-1, or -128..127 short: A value occupies 2 bytes (16 bits). The range of values is -2^15..2^15-1 int: A value occupies 4 bytes (32 bits). The range of values is -2^31..2^31-1 long: A value occupies 8 bytes (64 bits). The range of values is -2^63..2^63-1 and two “floating-point” types, whose values are approximations to the real numbers: float: A value occupies 4 bytes (32 bits). double: A value occupies 8 bytes (64 bits). Values of the integral types are maintained in two’s complement notation (see the dictionary entry for two’s complement notation). A discussion of floating-point values is outside the scope of this website, except to say that some bits are used for the mantissa and some for the exponent and that infinity and NaN (not a number) are both floating-point values. We don’t discuss this further. Generally, one uses mainly types int and double. But if you are declaring a large array and you know that the values fit in a byte, you can save ¾ of the space using a byte array instead of an int array, e.g. byte[] b= new byte[1000]; Operations on the primitive integer types Types byte and short have no operations. Instead, operations on their values int and long operations are treated as if the values were of type int.
    [Show full text]
  • Design of 32 Bit Floating Point Addition and Subtraction Units Based on IEEE 754 Standard Ajay Rathor, Lalit Bandil Department of Electronics & Communication Eng
    International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 2 Issue 6, June - 2013 Design Of 32 Bit Floating Point Addition And Subtraction Units Based On IEEE 754 Standard Ajay Rathor, Lalit Bandil Department of Electronics & Communication Eng. Acropolis Institute of Technology and Research Indore, India Abstract Precision format .Single precision format, Floating point arithmetic implementation the most basic format of the ANSI/IEEE described various arithmetic operations like 754-1985 binary floating-point arithmetic addition, subtraction, multiplication, standard. Double precision and quad division. In science computation this circuit precision described more bit operation so at is useful. A general purpose arithmetic unit same time we perform 32 and 64 bit of require for all operations. In this paper operation of arithmetic unit. Floating point single precision floating point arithmetic includes single precision, double precision addition and subtraction is described. This and quad precision floating point format paper includes single precision floating representation and provide implementation point format representation and provides technique of various arithmetic calculation. implementation technique of addition and Normalization and alignment are useful for subtraction arithmetic calculations. Low operation and floating point number should precision custom format is useful for reduce be normalized before any calculation [3]. the associated circuit costs and increasing their speed. I consider the implementation ofIJERT IJERT2. Floating Point format Representation 32 bit addition and subtraction unit for floating point arithmetic. Floating point number has mainly three formats which are single precision, double Keywords: Addition, Subtraction, single precision and quad precision. precision, doubles precision, VERILOG Single Precision Format: Single-precision HDL floating-point format is a computer number 1.
    [Show full text]
  • C++ Data Types
    Software Design & Programming I Starting Out with C++ (From Control Structures through Objects) 7th Edition Written by: Tony Gaddis Pearson - Addison Wesley ISBN: 13-978-0-132-57625-3 Chapter 2 (Part II) Introduction to C++ The char Data Type (Sample Program) Character and String Constants The char Data Type Program 2-12 assigns character constants to the variable letter. Anytime a program works with a character, it internally works with the code used to represent that character, so this program is still assigning the values 65 and 66 to letter. Character constants can only hold a single character. To store a series of characters in a constant we need a string constant. In the following example, 'H' is a character constant and "Hello" is a string constant. Notice that a character constant is enclosed in single quotation marks whereas a string constant is enclosed in double quotation marks. cout << ‘H’ << endl; cout << “Hello” << endl; The char Data Type Strings, which allow a series of characters to be stored in consecutive memory locations, can be virtually any length. This means that there must be some way for the program to know how long the string is. In C++ this is done by appending an extra byte to the end of string constants. In this last byte, the number 0 is stored. It is called the null terminator or null character and marks the end of the string. Don’t confuse the null terminator with the character '0'. If you look at Appendix A you will see that the character '0' has ASCII code 48, whereas the null terminator has ASCII code 0.
    [Show full text]
  • Floating Point Representation (Unsigned) Fixed-Point Representation
    Floating point representation (Unsigned) Fixed-point representation The numbers are stored with a fixed number of bits for the integer part and a fixed number of bits for the fractional part. Suppose we have 8 bits to store a real number, where 5 bits store the integer part and 3 bits store the fractional part: 1 0 1 1 1.0 1 1 $ 2& 2% 2$ 2# 2" 2'# 2'$ 2'% Smallest number: Largest number: (Unsigned) Fixed-point representation Suppose we have 64 bits to store a real number, where 32 bits store the integer part and 32 bits store the fractional part: "# "% + /+ !"# … !%!#!&. (#(%(" … ("% % = * !+ 2 + * (+ 2 +,& +,# "# "& & /# % /"% = !"#× 2 +!"&× 2 + ⋯ + !&× 2 +(#× 2 +(%× 2 + ⋯ + ("%× 2 0 ∞ (Unsigned) Fixed-point representation Range: difference between the largest and smallest numbers possible. More bits for the integer part ⟶ increase range Precision: smallest possible difference between any two numbers More bits for the fractional part ⟶ increase precision "#"$"%. '$'#'( # OR "$"%. '$'#'(') # Wherever we put the binary point, there is a trade-off between the amount of range and precision. It can be hard to decide how much you need of each! Scientific Notation In scientific notation, a number can be expressed in the form ! = ± $ × 10( where $ is a coefficient in the range 1 ≤ $ < 10 and + is the exponent. 1165.7 = 0.0004728 = Floating-point numbers A floating-point number can represent numbers of different order of magnitude (very large and very small) with the same number of fixed bits. In general, in the binary system, a floating number can be expressed as ! = ± $ × 2' $ is the significand, normally a fractional value in the range [1.0,2.0) .
    [Show full text]
  • Floating Point Numbers
    Floating Point Numbers CS031 September 12, 2011 Motivation We’ve seen how unsigned and signed integers are represented by a computer. We’d like to represent decimal numbers like 3.7510 as well. By learning how these numbers are represented in hardware, we can understand and avoid pitfalls of using them in our code. Fixed-Point Binary Representation Fractional numbers are represented in binary much like integers are, but negative exponents and a decimal point are used. 3.7510 = 2+1+0.5+0.25 1 0 -1 -2 = 2 +2 +2 +2 = 11.112 Not all numbers have a finite representation: 0.110 = 0.0625+0.03125+0.0078125+… -4 -5 -8 -9 = 2 +2 +2 +2 +… = 0.00011001100110011… 2 Computer Representation Goals Fixed-point representation assumes no space limitations, so it’s infeasible here. Assume we have 32 bits per number. We want to represent as many decimal numbers as we can, don’t want to sacrifice range. Adding two numbers should be as similar to adding signed integers as possible. Comparing two numbers should be straightforward and intuitive in this representation. The Challenges How many distinct numbers can we represent with 32 bits? Answer: 232 We must decide which numbers to represent. Suppose we want to represent both 3.7510 = 11.112 and 7.510 = 111.12. How will the computer distinguish between them in our representation? Excursus – Scientific Notation 913.8 = 91.38 x 101 = 9.138 x 102 = 0.9138 x 103 We call the final 3 representations scientific notation. It’s standard to use the format 9.138 x 102 (exactly one non-zero digit before the decimal point) for a unique representation.
    [Show full text]
  • Floating Point Numbers Dr
    Numbers Representaion Floating point numbers Dr. Tassadaq Hussain Riphah International University Real Numbers • Two’s complement representation deal with signed integer values only. • Without modification, these formats are not useful in scientific or business applications that deal with real number values. • Floating-point representation solves this problem. Floating-Point Representation • If we are clever programmers, we can perform floating-point calculations using any integer format. • This is called floating-point emulation, because floating point values aren’t stored as such; we just create programs that make it seem as if floating- point values are being used. • Most of today’s computers are equipped with specialized hardware that performs floating-point arithmetic with no special programming required. —Not embedded processors! Floating-Point Representation • Floating-point numbers allow an arbitrary number of decimal places to the right of the decimal point. For example: 0.5 0.25 = 0.125 • They are often expressed in scientific notation. For example: 0.125 = 1.25 10-1 5,000,000 = 5.0 106 Floating-Point Representation • Computers use a form of scientific notation for floating-point representation • Numbers written in scientific notation have three components: Floating-Point Representation • Computer representation of a floating-point number consists of three fixed-size fields: • This is the standard arrangement of these fields. Note: Although “significand” and “mantissa” do not technically mean the same thing, many people use these terms interchangeably. We use the term “significand” to refer to the fractional part of a floating point number. Floating-Point Representation • The one-bit sign field is the sign of the stored value.
    [Show full text]
  • A Decimal Floating-Point Speciftcation
    A Decimal Floating-point Specification Michael F. Cowlishaw, Eric M. Schwarz, Ronald M. Smith, Charles F. Webb IBM UK IBM Server Division P.O. Box 31, Birmingham Rd. 2455 South Rd., MS:P310 Warwick CV34 5JL. UK Poughkeepsie, NY 12601 USA [email protected] [email protected] Abstract ing is required. In the fixed point formats, rounding must be explicitly applied in software rather than be- Even though decimal arithmetic is pervasive in fi- ing provided by the hardware. To address these and nancial and commercial transactions, computers are other limitations, we propose implementing a decimal stdl implementing almost all arithmetic calculations floating-point format. But what should this format be? using binary arithmetic. As chip real estate becomes This paper discusses the issues of defining a decimal cheaper it is becoming likely that more computer man- floating-point format. ufacturers will provide processors with decimal arith- First, we consider the goals of the specification. It metic engines. Programming languages and databases must be compliant with standards already in place. are expanding the decimal data types available whale One standard we consider is the ANSI X3.274-1996 there has been little change in the base hardware. As (Programming Language REXX) [l]. This standard a result, each language and application is defining a contains a definition of an integrated floating-point and different arithmetic and few have considered the efi- integer decimal arithmetic which avoids the need for ciency of hardware implementations when setting re- two distinct data types and representations. The other quirements. relevant standard is the ANSI/IEEE 854-1987 (Radix- In this paper, we propose a decimal format which Independent Floating-point Arithmetic) [a].
    [Show full text]
  • Princeton University COS 217: Introduction to Programming Systems C Primitive Data Types
    Princeton University COS 217: Introduction to Programming Systems C Primitive Data Types Type: int Description: A (positive or negative) integer. Size: System dependent. On CourseLab with gcc217: 4 bytes. Example Variable Declarations: int iFirst; signed int iSecond; Example Literals (assuming size is 4 bytes): C Literal Binary Representation Note 123 00000000 00000000 00000000 01111011 decimal form -123 11111111 11111111 11111111 10000101 negative form 0173 00000000 00000000 00000000 01111011 octal form 0x7B 00000000 00000000 00000000 01111011 hexadecimal form 2147483647 01111111 11111111 11111111 11111111 largest -2147483648 10000000 00000000 00000000 00000000 smallest Type: unsigned int Description: A non-negative integer. Size: System dependent. sizeof(unsigned int) == sizeof(int). On CourseLab with gcc217: 4 bytes. Example Variable Declaration: unsigned int uiFirst; unsigned uiSecond; Example Literals (assuming size is 4 bytes): C Literal Binary Representation Note 123U 00000000 00000000 00000000 01111011 decimal form 0173U 00000000 00000000 00000000 01111011 octal form 0x7BU 00000000 00000000 00000000 01111011 hexadecimal form 4294967295U 11111111 11111111 11111111 11111111 largest 0U 00000000 00000000 00000000 00000000 smallest Type: long Description: A (positive or negative) integer. Size: System dependent. sizeof(long) >= sizeof(int). On CourseLab with gcc217: 8 bytes. Example Variable Declarations: long lFirst; long int iSecond; signed long lThird; signed long int lFourth; Page 1 of 5 Example Literals (assuming size is 8 bytes):
    [Show full text]
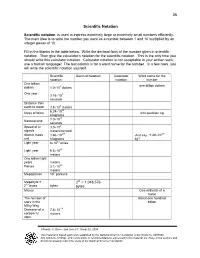
  • 36 Scientific Notation
    36 Scientific Notation Scientific notation is used to express extremely large or extremely small numbers efficiently. The main idea is to write the number you want as a number between 1 and 10 multiplied by an integer power of 10. Fill in the blanks in the table below. Write the decimal form of the number given in scientific notation. Then give the calculator’s notation for the scientific notation. This is the only time you should write this calculator notation. Calculator notation is not acceptable in your written work; use a human language! The last column is for a word name for the number. In a few rows, you will write the scientific notation yourself. Scientific Decimal Notation Calculator Word name for the notation notation number One billion one billion dollars dollars 1.0 ×10 9 dollars One year 3.16 ×10 7 seconds Distance from earth to moon 3.8 ×10 8 meters 6.24 ×10 23 Mass of Mars 624 sextillion kg kilograms 1.0 ×10 -9 Nanosecond seconds 8 Speed of tv 3.0 ×10 signals meters/second -27 -27 Atomic mass 1.66 ×10 Just say, “1.66 ×10 unit kilograms kg”! × 12 Light year 6 10 miles 15 Light year 9.5 ×10 meters One billion light years meters 16 Parsec 3.1 ×10 meters 6 Megaparsec 10 parsecs Megabyte = 220 = 1,048,576 20 2 bytes bytes bytes Micron One millionth of a meter The number of About one hundred stars in the billion Milky Way -14 Diameter of a 7.5 ×10 carbon-12 meters atom Rosalie A.
    [Show full text]
  • Floating Point CSE410, Winter 2017
    L07: Floating Point CSE410, Winter 2017 Floating Point CSE 410 Winter 2017 Instructor: Teaching Assistants: Justin Hsia Kathryn Chan, Kevin Bi, Ryan Wong, Waylon Huang, Xinyu Sui L07: Floating Point CSE410, Winter 2017 Administrivia Lab 1 due next Thursday (1/26) Homework 2 released today, due 1/31 Lab 0 scores available on Canvas 2 L07: Floating Point CSE410, Winter 2017 Unsigned Multiplication in C u ••• Operands: * bits v ••• True Product: u · v ••• ••• bits Discard bits: UMultw(u , v) ••• bits Standard Multiplication Function . Ignores high order bits Implements Modular Arithmetic w . UMultw(u , v)= u ∙ v mod 2 3 L07: Floating Point CSE410, Winter 2017 Multiplication with shift and add Operation u<<k gives u*2k . Both signed and unsigned u ••• Operands: bits k * 2k 0 ••• 0 1 0 ••• 0 0 True Product: bits u · 2k ••• 0 ••• 0 0 k Discard bits: bits UMultw(u , 2 ) ••• 0 ••• 0 0 k TMultw(u , 2 ) Examples: . u<<3 == u * 8 . u<<5 - u<<3 == u * 24 . Most machines shift and add faster than multiply • Compiler generates this code automatically 4 L07: Floating Point CSE410, Winter 2017 Number Representation Revisited What can we represent in one word? . Signed and Unsigned Integers . Characters (ASCII) . Addresses How do we encode the following: . Real numbers (e.g. 3.14159) . Very large numbers (e.g. 6.02×1023) Floating . Very small numbers (e.g. 6.626×10‐34) Point . Special numbers (e.g. ∞, NaN) 5 L07: Floating Point CSE410, Winter 2017 Floating Point Topics Fractional binary numbers IEEE floating‐point standard Floating‐point operations and rounding Floating‐point in C There are many more details that we won’t cover .
    [Show full text]
  • Fortran Reference Guide
    FORTRAN REFERENCE GUIDE Version 2017 TABLE OF CONTENTS Preface............................................................................................................xiv Audience Description.........................................................................................xiv Compatibility and Conformance to Standards........................................................... xiv Organization.................................................................................................... xv Hardware and Software Constraints.......................................................................xvi Conventions.................................................................................................... xvi Related Publications.........................................................................................xvii Chapter 1. Language Overview............................................................................... 1 1.1. Elements of a Fortran Program Unit.................................................................. 1 1.1.1. Fortran Statements................................................................................. 1 1.1.2. Free and Fixed Source............................................................................. 2 1.1.3. Statement Ordering................................................................................. 2 1.2. The Fortran Character Set.............................................................................. 3 1.3. Free Form Formatting..................................................................................
    [Show full text]