Evaluation of Spatial Pattern of Altered Flow Regimes on a River Network Using a Distributed Hydrological Model
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Vol2 Case History English(1-206)
Renewal & Upgrading of Hydropower Plants IEA Hydro Technical Report _______________________________________ Volume 2: Case Histories Report March 2016 IEA Hydropower Agreement: Annex XI AUSTRALIA USA Table of contents㸦Volume 2㸧 ࠙Japanࠚ Jp. 1 : Houri #2 (Miyazaki Prefecture) P 1 㹼 P 5ۑ Jp. 2 : Kikka (Kumamoto Prefecture) P 6 㹼 P 10ۑ Jp. 3 : Hidaka River System (Hokkaido Electric Power Company) P 11 㹼 P 19ۑ Jp. 4 : Kurobe River System (Kansai Electric Power Company) P 20 㹼 P 28ۑ Jp. 5 : Kiso River System (Kansai Electric Power Company) P 29 㹼 P 37ۑ Jp. 6 : Ontake (Kansai Electric Power Company) P 38 㹼 P 46ۑ Jp. 7 : Shin-Kuronagi (Kansai Electric Power Company) P 47 㹼 P 52ۑ Jp. 8 : Okutataragi (Kansai Electric Power Company) P 53 㹼 P 63ۑ Jp. 9 : Okuyoshino / Asahi Dam (Kansai Electric Power Company) P 64 㹼 P 72ۑ Jp.10 : Shin-Takatsuo (Kansai Electric Power Company) P 73 㹼 P 78ۑ Jp.11 : Yamasubaru , Saigo (Kyushu Electric Power Company) P 79 㹼 P 86ۑ Jp.12 : Nishiyoshino #1,#2(Electric Power Development Company) P 87 㹼 P 99ۑ Jp.13 : Shin-Nogawa (Yamagata Prefecture) P100 㹼 P108ۑ Jp.14 : Shiroyama (Kanagawa Prefecture) P109 㹼 P114ۑ Jp.15 : Toyomi (Tohoku Electric Power Company) P115 㹼 P123ۑ Jp.16 : Tsuchimurokawa (Tokyo Electric Power Company) P124㹼 P129ۑ Jp.17 : Nishikinugawa (Tokyo Electric Power Company) P130 㹼 P138ۑ Jp.18 : Minakata (Chubu Electric Power Company) P139 㹼 P145ۑ Jp.19 : Himekawa #2 (Chubu Electric Power Company) P146 㹼 P154ۑ Jp.20 : Oguchi (Hokuriku Electric Power Company) P155 㹼 P164ۑ Jp.21 : Doi (Chugoku Electric Power Company) -

The Federal Capital Territory Reduction of Non-Revenue Water Project
Federal Capital Territory Administration Federal Capital Territory Administration Federal Capital Territory Water Board Federal Capital Territory Water Board Federal RepublicCapital Territory of Nigeria Administration Federal Republic of Nigeria Federal Capital Territory Water Board Federal Republic of Nigeria THE FEDERAL CAPITAL TERRITORY REDUCTIONTHE FEDERAL OF NON-REVENUECAPITAL TERRITORY WATER REDUCTION OFPROJECT NON-REVENUE WATER PROJECTIN FEDERAL REPUBLICIN OF NIGERIA FEDERALPROJECT REPUBLIC FINAL REPORTOF NIGERIA (SUPPORTINGPROJECT FINALREPORT, REPORT VOL. 2/2) (SUPPORTING REPORT, VOL. 2/2) January 2019 January 2019 January 2019 Japan International Cooperation Agency Japan International Cooperation Agency Yachiyo Engineering Co., Ltd Japan YachiyoInternational Engineering Cooperation Co., Ltd Agency GE Yokohama Water Co., Ltd GEGE YachiyoYokohama Engineering Water Co., Co., Ltd Ltd JR JR GEJR Yokohama Water Co., Ltd 19-005 1919-005 - 005 JR 19-005 Federal Capital Territory Administration Federal Capital Territory Administration Federal Capital Territory Water Board Federal Capital Territory Water Board Federal RepublicCapital Territory of Nigeria Administration Federal Republic of Nigeria Federal Capital Territory Water Board Federal Republic of Nigeria THE FEDERAL CAPITAL TERRITORY REDUCTIONTHE FEDERAL OF NON-REVENUECAPITAL TERRITORY WATER REDUCTION OFPROJECT NON-REVENUE WATER PROJECTIN FEDERAL REPUBLICIN OF NIGERIA FEDERALPROJECT REPUBLIC FINAL REPORTOF NIGERIA (SUPPORTINGPROJECT FINALREPORT, REPORT VOL. 2/2) (SUPPORTING REPORT, -

Rising Sun Weekly Email Dispatch
March 19, 2018 + Volume 3, No. 2 SERVING THE U.S. ARMY JAPAN COMMUNITY http://www.facebook.com/USAGJ Rising Sun Weekly Email Dispatch INSIDE THIS VOLUME USAG Japan Social Media Network: Cover: Women's History Month Facebook - http://www.facebook.com/usagj 2 Airbag Recall Vimeo - http://www.vimeo.com/usagj 4 Honoring Vietnam Veterans Twitter - http://www.twitter.com/usagjapan 5 2018 Road Tax Program Flickr - http://www.flickr.com/usagj 6 Read Across America Campaign YouTube - http://www.youtube.com/usagjapan 8 Road Closures Pinterest- http://www.pinterest.com/garrisonjapan/ 9 DFAC Menu Slideshare - http://www.slideshare.net/usagj March 19, 2018 + Volume 3, No. 2 SERVING THE U.S. ARMY JAPAN COMMUNITY http://www.facebook.com/USAGJ Rising Sun Weekly Email Dispatch Safety Alert: Airbag Recall Hot Voting News The manufacturer of Takata airbags is Are you or your friends voting absentee recalling millions of vehicles due to in the Arizona District 8 Special General airbag defects. election? Recall repairs for affected vehicles are You must be registered to vote by March FREE and should be done before May 26, 2018. That's in less than two weeks! 1, 2018 to pass JCI renewal inspections happening on or after this date. Do it now at http://FVAP.gov/Arizona Visit https://www.nhtsa.gov/recall-spotlight/takata-air-bags (ENGLISH) or https:// It's a midterm election year, and you don't www.jaspa.or.jp/portals/recallsearch/index.html (JAPANESE) to determine if your have to wait until November to have your vehicle falls under the recall. -

OC (2015) Evaluation of Spatial Pattern of Altered Flow Regimes On
RESEARCH ARTICLE Evaluation of Spatial Pattern of Altered Flow Regimes on a River Network Using a Distributed Hydrological Model Masahiro Ryo1¤a*, Yuichi Iwasaki2¤b, Chihiro Yoshimura1, Oliver C. Saavedra V.1 1 Department of Civil Engineering, Tokyo Institute of Technology, Meguro-ku, Tokyo, Japan, 2 Department of Fish, Wildlife, and Conservation Biology, Colorado State University, Fort Collins, Colorado, United States of America ¤a Current Address: Department of Aquatic Ecology, Eawag, Duebendorf, Switzerland ¤b Current Address: Research Center for Life and Environmental Sciences, Toyo University, Oura, Gunma, Japan * [email protected] Abstract Alteration of the spatial variability of natural flow regimes has been less studied than that of OPEN ACCESS the temporal variability, despite its ecological importance for river ecosystems. Here, we aimed to quantify the spatial patterns of flow regime alterations along a river network in the Citation: Ryo M, Iwasaki Y, Yoshimura C, Saavedra V. OC (2015) Evaluation of Spatial Pattern of Altered Sagami River, Japan, by estimating river discharge under natural and altered flow condi- Flow Regimes on a River Network Using a tions. We used a distributed hydrological model, which simulates hydrological processes Distributed Hydrological Model. PLoS ONE 10(7): spatiotemporally, to estimate 20-year daily river discharge along the river network. Then, 33 e0133833. doi:10.1371/journal.pone.0133833 hydrologic indices (i.e., Indicators of Hydrologic Alteration) were calculated from the simu- Editor: Zhong-Ke Gao, Tianjin University, CHINA lated discharge to estimate the spatial patterns of their alterations. Some hydrologic indices Received: January 8, 2015 were relatively well estimated such as the magnitude and timing of maximum flows, monthly Accepted: July 2, 2015 median flows, and the frequency of low and high flow pulses. -

Japan's Experiences on Water Supply Development
Cover photos Upper left: Leakage survey around 1949, Nagoya City Waterworks and Sewerage Bureau. Upper right: Construction site of water distribution pipe in 1912, Nagoya City Waterworks and Sewerage Bureau. Bottom left: Carrying water before the development of water supply, Susumu Hani, the film “Water in Our Life,” Iwanami Productions, 1952. Lower middle: Water tanker for the drought of 1978, Fukuoka City Waterworks Bureau. Bottom right: Ogouchi Dam without water during drought of 1964, Bureau of Waterworks, Tokyo Metropolitan Government. Japan's Experiences on Water Supply Development March 2017 Japan International Cooperation Agency Water Partners Jp Co., Ltd. Nihon Suido Consultants Co., Ltd. Preface Access to safe water is an essential part of human rights and the foundation for a healthy life. However, even today, the world witnesses many instances of people lacking access to this essential commodity. To counter this situation, a new global agenda - the Sustainable Development Goals (SDGs) - was unanimously adopted by the member states of the United Nations in 2015. The agenda included a dedicated goal on water (Goal 6) that aims to “ensure availability and sustainable management of water and sanitation for all.” Target 6.1 of Goal 6 estimates that “by 2030, achieve universal and equitable access to safe and affordable drinking water for all.” Japan has been contributing for years to the development of the water supply sector. When Japan started to construct modern water supply systems, it faced vast challenges with regard to expansion of service coverage and improvement of service quality, as is the case in most developing countries. However, it overcame these challenges with the help of proactive efforts, including the introduction of the overseas technology, and achieved the objective of nationwide coverage of safe water supply. -

Rising Sun Weekly Email Dispatch
March 12, 2018 + Volume 3, No. 1 SERVING THE U.S. ARMY JAPAN COMMUNITY http://www.facebook.com/USAGJ Rising Sun Weekly Email Dispatch INSIDE THIS VOLUME USAG Japan Social Media Network: C Easter Egg Hunt Facebook - http://www.facebook.com/usagj 2 Local Nationals Town Hall Vimeo - http://www.vimeo.com/usagj 4 Lent-Easter Events 2018 Twitter - http://www.twitter.com/usagjapan 5 2018 Road Tax Program Flickr - http://www.flickr.com/usagj 6 Read Across America Campaign YouTube - http://www.youtube.com/usagjapan 7 MWR March Calendar Pinterest- http://www.pinterest.com/garrisonjapan/ 9 DFAC Menu Slideshare - http://www.slideshare.net/usagj March 12, 2018 + Volume 3, No. 1 SERVING THE U.S. ARMY JAPAN COMMUNITY http://www.facebook.com/USAGJ Rising Sun Weekly Email Dispatch USAJOBS Adopts New Login Hot Voting News USAJOBS has adopted Login.Gov as a platform to make the federal application As we begin the month of March, we also process easier, more secure. What does this begin the 2018 Election Season. change mean to your USAJOBS account? As of March 6, 2018 there are 16 different States holding Primaries or Special Elections over the next 90 days in preparation for the Nothing will happen to the information Nov. 6, 2018 General Election. already stored in your USAJOBS account and profile. You will be able to keep all of your Please check https://www.fvap.gov/guide/ applications as well saved searches and job upcoming-elections to see if your State is announcements. one of them. Once you set up a login.gov account, you will connect the account to your USAJOBS If you requested your absentee ballot and profile. -

And the Muda River Basin (Malaysia)
resources Article Comparative Research on River Basin Management in the Sagami River Basin (Japan) and the Muda River Basin (Malaysia) Lay Mei Sim 1,*, Akio Onishi 2, Olivier Gervais 3 and Ngai Weng Chan 1 1 School of Humanities, Geography Department, University Science of Malaysia, Penang 11800, Malaysia; [email protected] 2 School of Data Science, Yokohama City University, 22-2 Seto, Kanazawa-ku, Yokohama-shi 236-0027, Japan; [email protected] 3 Department of Integrative Genomics, Tohoku Medical Megabank Organization, Tohoku University, 2-1 Seiryo-machi, Aoba-ku, Sendai, Miyagi 980-8573, Japan; [email protected] * Correspondence: [email protected]; Tel.: +60-125-875-690 Received: 20 March 2018; Accepted: 15 May 2018; Published: 24 May 2018 Abstract: In the world, river basins often interwoven into two or more states or prefectures and because of that, disputes over water are common. Nevertheless, not all shared river basins are associated with water conflicts. Rivers in Japan and Malaysia play a significant role in regional economic development. They also play a significant role as water sources for industrial, domestic, agricultural, aquaculture, hydroelectric power generation, and the environment. The research aim is to determine the similarities and differences between the Sagami and Muda River Basins in order to have a better understanding of the governance needed for effectively implementing the lessons drawn from the Sagami River Basin for improving the management of the Muda River Basin in Malaysia. This research adopts qualitative and quantitative approaches. Semi-structured interviews were held with the key stakeholders from both basins and show that Japan has endeavored to present policy efforts to accommodate the innovative approaches in the management of their water resources, including the establishment of a river basin council. -
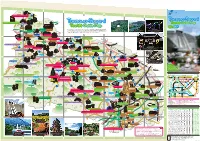
Open to the Public
A B C D E F 521 Wada no Sato Experience Center "Village House" G H Mt. Jimba Tanzawa-Sagami 100 Japanese Rural Villages・ Sanogawa Area To Hachioji Tanzawa Sagami Jimba no Yu - Tourist Guide Map 522 1 Touristst GuGuiddee Mapp 1 たび相模 Ishii House 旅 丹沢・相模 観光ナビ Expresswa uo y Ch Sagamiko-Higashi Kanagawa Prefectural Government Website: Tanzawa-Sagami Tourist Guide To Kofu Obarajuku Honjin Midori's Love Letter Lake Tsukui Ogura Bridge Sagamiko IC IC provides sightseeing information: places to visit, souvenirs to purchase, and Midori Ward Sagamihara City (Fujino area) Midori Ward Sagamihara City (Tsukui area) Midori Ward Sagamihara City (Shiroyama area) K MAP - MAP - MAP - osh A 2 /D 2 Guide: Nature /E 2 Guide: History u Higway e in . It's updated regularly. Check it out online! L 20 To Takao events to experience 20 uo Ch Fujino JR Sagamiko Lake Sagami Yoshino-juku Fujiya Sagamiko Memorial Hall Prefectural Sagamiko Park To Hachioji Lake Shiroyama Shiroyama lake promenade To Hachioji To Hachioji Art Walk Sagamiko Resort Pleasure Forest Shokakuji Temple 515 Sagamihara City Mt.Sekiro To Chofu Ozaki Gakudo Memorial House Midori Ward Lake Tsukui 413 (Shiroyama Area) Hashimoto e Fujino Hot Springs Higashiotaru no Yu Lin ihara gam io Sa 2 Prefectural Fujino Art House Sagamihara City 412 Sagamihara City Ke 2 517 J Midori Ward Midori Ward R Y ok Obarajuku Honjin Shinohara no Sato Center oh (Sagamiko Area) am a Midori Ward Sagamihara City (Sagamiko area) Lin Ogura Bridge e /MAP C-1 Guide: History Fujino Yamanami Hot Springs IC Sagamihara Sagamigawa Nature Village Park 518 Sagamihara Prefectural Tsukuiko-Shiroyama Park 508 Minami- 129 Hashimoto Sagamihara City Yabe Kami-Ooshima Campgrounds Midori Ward 16 Doshi Riv. -

Kanagawa Prefectural Aikawa Park
Kanagawa sightseeing charm creation conference Central of <Flowers> the Prefecture Aikawa Town Renowned spot for azaleas, the official flower of Aikawa Town Tourist Attraction No. 1349 Kanagawa Prefectural Aikawa Park Kanagawa Prefectural Aikawa Park is a terraced park which extends directly below Miyagase Dam, one of the largest gravity type concrete dams in Japan. The park's expansive grounds, which cover 51 hectares, have been planted with Explanation of 40,000 azaleas with a total of 40 varieties. Visitors to the park can enjoy impressive Tourist Attraction seasonal sights, from colorful slopes of azalea flowers that come into bloom in spring to breezy hills with stunning views of Yokohama's famous landmarks on clear days. Aikawa Park Azalea Festival is held here every year on April 29. Visitors can enjoy a variety of beautiful seasonal flowers and sights,including selling point 40,000 azaleas with a total of 40 varieties. Address 5423 Hanbara, Aikawa-machi, Aiko-gun, Kanagawa Opening Hours 8:30 am to 6:00 pm (April - September) 8:30 am to 5:00 pm (October - March the following year) Parking fees are paid in advance. Standard size cars: ¥500; medium-sized / large vehicles: ¥1,500; two-wheeled vehicles: ¥100 Availability of Parking Parking fees include a ¥20 contribution to a greenery fund. * Parking is free of charge during Azalea Festival days. URL http://www.aikawa-park.jp/publics/index/4/ Recommended Season End of April - end of May Access (period when the azaleas are in bloom) From Hon-Atsugi Station on the Odakyu Group/Individual Mark Group Individual Odawara Line, take a Kanagawa Chuo Kotsu Bus bound for Hanbara via the Target Regions Europe, North America, Oceania, Asia Center for 60 minutes, and walk from Hanbara Bus stop for 20 minutes. -

Evaluation of Spatial Pattern of Altered Flow Regimes on a River Network Using a Distributed Hydrological Model
Research Collection Journal Article Evaluation of Spatial Pattern of Altered Flow Regimes on a River Network Using a Distributed Hydrological Model Author(s): Ryo, Masahiro; Iwasaki, Yuichi; Yoshimura, Chihiro; Saavedra Valeriano, Oliver C. Publication Date: 2015-07-24 Permanent Link: https://doi.org/10.3929/ethz-b-000110936 Originally published in: PLoS ONE 10(7), http://doi.org/10.1371/journal.pone.0133833 Rights / License: Creative Commons Attribution 4.0 International This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library RESEARCH ARTICLE Evaluation of Spatial Pattern of Altered Flow Regimes on a River Network Using a Distributed Hydrological Model Masahiro Ryo1¤a*, Yuichi Iwasaki2¤b, Chihiro Yoshimura1, Oliver C. Saavedra V.1 1 Department of Civil Engineering, Tokyo Institute of Technology, Meguro-ku, Tokyo, Japan, 2 Department of Fish, Wildlife, and Conservation Biology, Colorado State University, Fort Collins, Colorado, United States of America ¤a Current Address: Department of Aquatic Ecology, Eawag, Duebendorf, Switzerland ¤b Current Address: Research Center for Life and Environmental Sciences, Toyo University, Oura, Gunma, Japan * [email protected] Abstract Alteration of the spatial variability of natural flow regimes has been less studied than that of OPEN ACCESS the temporal variability, despite its ecological importance for river ecosystems. Here, we aimed to quantify the spatial patterns of flow regime alterations along a river network in the Citation: Ryo M, Iwasaki Y, Yoshimura C, Saavedra V. OC (2015) Evaluation of Spatial Pattern of Altered Sagami River, Japan, by estimating river discharge under natural and altered flow condi- Flow Regimes on a River Network Using a tions. -

Resource Mobilization Information Digest No 215 September 2013 Environmental Fiscal Reforms in Japan
o Resource Mobilization Information Digest N 215 September 2013 Environmental fiscal reforms in Japan Contents Conserving forest environments with tax revenues ..................................................................................... 2 Tochigi Prefectural Tax for Healthy Forest-Making ...................................................................................... 3 Increased tax rates for the Prefectural Inhabitant Tax on individuals to fund water source environment programms .................................................................................................................................................... 7 Kanagawa Basic Policies for Conservation and Restoration of Water Source Environment .................... 9 Kanagawa Five-Year Action Plan for Conservation and Restoration of Water Source Environment ..... 10 Japan indicated1 that some cases have been introduced at the following website: http://www.biodic.go.jp/biodiversity/shiraberu/policy/pes/en/index.html Conserving forest environments with tax revenues Forests provide the services of producing substances that we use as wood and food, recharging water, preventing floods and sediment disaster in large storms, absorbing CO2 and mitigating climate change as well as providing habitats for diverse living creatures and sites for recreation and environmental education. Forests cover two-thirds of Japan. Although forest coverage has not changed in over 40 years, decreased demand for domestic wood and lower timber prices, tree thinning and other forest -

Climatic Zone: Subjects: Effects: Project Name: Country
IEA Hydropower Implementing Agreement Annex VIII - Hydropower Good Practices: Environmental Mitigation Measures and Benefits Case Study 14-03: Development of Regional Industries – Miyagase Dam, Japan Key Issues: 14- Development of Regional Industries 1-Biological Diversity 7-Resttlement Climatic Zone: Cf : Temperate Humid Climate Subjects: - Development of Sightseeing and Other Facilities to Vitalize the Area Around the Dam Effects: - Nature preservation - Stimulation of local industries through development of sightseeing spots Project Name: Miyagase Dam Country ::: Kanagawa Prefecture, Japan(Asia) Implementing Party & Period - Project: the Ministry of Land, Infrastructure and Transport 1987.11 through 2001.4 - Good Practice: the Ministry of Land, Infrastructure and Transport 2001.4 - Keywords: Environmental protection, biotope, stimulation of local development, vitalization of the water source area, tourism development Abstract ::: Activities, including the development of biotopes, were conducted to restore the natural environment in the area impacted by the dam development project. In addition, activities to develop sightseeing facilities such as an information center were conducted after completion of the dam to stimulate local development. The number of tourists visiting Kiyokawa Village, where the dam had been constructed, and the total tourist spending increased more than five times compared to the figures before the implementation of the project. (See Fig. 4) 1. Outline of the Project The Miyagase Dam is a concrete gravity dam with a height of 156 m, a volume of approximately 2 million m 3 and a gross storage capacity of approximately 200 million m 3. It was constructed on the Nakatsu River, which is a tributary of the Sagami River, a first-class river originating in the Tanzawa Mountain Range located in the western part of Kanagawa Prefecture, to serve the multiple purposes of flood control, river environment improvement, city water supply and power generation.