DOCSLIB.ORG

A Dirac Delta Operator

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Dirac Delta Operator Mathematics and Statistics 9(2): 179-187, 2021 http://www.hrpub.org DOI: 10.13189/ms.2021.090213 A Dirac Delta Operator Juan Carlos Ferrando Centro de Investigacion Operativa, Universidad Miguel Hernandez, E-03202 Elche, Spain Received February 1, 2021; Revised March 18, 2021; Accepted April 9, 2021 Cite This Paper in the following Citation Styles (a): [1] Juan Carlos Ferrando, ”A Dirac Delta Operator,” Mathematics and Statistics, Vol.9, No.2, pp. 179-187, 2021. DOI: 10.13189/ms.2021.090213. (b): Juan Carlos Ferrando, (2021). A Dirac Delta Operator. Mathematics and Statistics, 9(2), 179-187. DOI: 10.13189/ms.2021.090213. Copyright ©2021 by authors, all rights reserved. Authors agree that this article remains permanently open access under the terms of the Creative Commons Attribution License 4.0 International License Abstract If T is a (densely defined) self-adjoint opera- operator λ 7! δ (λI − T ) at T by tor acting on a complex Hilbert space H and I stands for Z +1 the identity operator, we introduce the delta function opera- f (T ) = f (λ) δ (λI − T ) dλ (1.1) tor λ 7! δ (λI − T ) at T . When T is a bounded operator, −∞ then δ (λI − T ) is an operator-valued distribution. If T is un- bounded, δ (λI − T ) is a more general object that still retains for each f 2 C (R), i. e., for each real-valued continuous func- some properties of distributions. We provide an explicit repre- tion f (λ). Here dλ is the Lebesgue measure of R, but the sentation of δ (λI − T ) in some particular cases, derive vari- right-hand side of (1.1) is not a true integral. If T is a bounded ous operative formulas involving δ (λI − T ) and give several operator, we shall see at once that δ (λI − T ) must be regarded applications of its usage in Spectral Theory as well as in Quan- as a vector-valued distribution, i. e., as a continuous linear map tum Mechanics. from the space D (R) into the locally convex space L (H) of Keywords Hilbert Space, Self-adjoint Operator, Vector- the bounded linear operators (endomorphisms) on H equipped valued Distribution, Spectral Measure with the strong operator topology [10, 11], whose action on f 2 D (R) we denote as an integral. If T is unbounded we shall see that δ (λI − T ) still retains some useful distributional-like properties. The previous equation means Z +1 δ (λI − T ) hy; f (T ) xi = f (λ) hy; δ (λI − T ) xi dλ (1.2) 1 The delta function −∞ The scalar delta ‘function’ λ 7! δ (λ − a) along with its for each (x; y) 2 D (f (T )) × H, where D (f (T )) stands for derivatives were introduced by Paul Dirac in [1], and later in the domain of the self-adjoint operator f (T ). [2, Section 15], although its definition can be traced back to Let us recall that if T is a (densely defined) self-adjoint op- Heaviside. The rigorous treatment of this object in the context erator, there is a unique spectral family fEλ : λ 2 Rg of self- of distribution theory is due to Laurent Schwartz [6, 12]. In this adjoint operators defined on the whole of H that satisfy (i) paper we extend the definition of δ (λ − a) from real numbers Eλ ≤ Eµ and EλEµ = Eλ for λ ≤ µ, (ii) lim!0+ Eλ+x = to self-adjoint operators on a Hilbert space H. We denote by Eλx, and (iii) limλ→−∞ Eλx = 0 and limλ!1 Eλx = x in H x 2 H D (T ) T D (R) =−! lim D ([−n; n]) the linear space of infinitely differen- for all . The domain of consists of those tiable complex-valued functions of compact support, equipped x 2 H such that with the inductive limit topology. As usual in physics we shall Z +1 2 2 assume that the scalar product in H is anti-linear for the first jλj d kEλxk < 1: variable. −∞ If T is a densely defined self-adjoint operator1 on H and I In this case, the spectral theorem (cf. [8, Section 107]) and stands for the identity operator, we define the delta function the Borel-measurable functional calculus provide a self-adjoint operator f (T ) defined by 1In what follows σ (T ) will denote the spectrum of T . Recall that the residual spectrum of a self-adjoint operator T is empty, so that σ (T ) = Z +1 σp (T ) [ σc (T ), where σp (T ) denotes the point spectrum (the eigenvalues) f (T ) = f (λ) dE (1.3) and σ (T ) the continuous spectrum of T . λ c −∞ 180 A Dirac Delta Operator for each Borel-measurable function f (λ), whose domain If λ 7! Y (λ − µ) denotes the unit step function at µ 2 R, given by Y (λ − µ) = 0 if λ < µ and Y (λ − µ) = 1 if λ ≥ µ, Z +1 2 2 since Eλ = Y (λI − T ) for each λ 2 R, formally D (f (T )) = x 2 H : jf (λ)j d kEλxk < 1 −∞ 0 dEλ/dλ = Y (λI − T ) : (1.7) is dense in H. Observe that if T is bounded, f (T ) need not So, from (1.6) and (1.7) we get Y 0 (λI − T ) = δ (λI − T ). be bounded. Moreover, since λ 7! Eλ is constant on the set R n σ (T ) of T , an open set in R, equation (1.3) tell us that Proposition 1. If T is a bounded self-adjoint operator on H f (λ) need not be defined on n σ (T ). 1 R and f 2 C (R), then Thanks to (1.3) the definition of δ (λI − T ) may be extended Z +1 to Borel-measurable functions by declaring that the equation 0 0 (1.1) holds for (x; y) 2 D (f (T )) × H and each Borel func- f (λ) δ (λI − T ) dλ = −f (T ) : −∞ tion f. But, by reasons that will become clear later, we shall restrict ourselves to those Borel functions which are continuous The same equality holds if T is unbounded but f 2 D (R). at each point of σp (T ). Moreover, working with the real and complex parts, no difficulty arises if the function f involved If T is a self-adjoint operator and f 2 Bp (R), then in the equation (1.1) is complex-valued (except that f (T ) is Z + 1 Z + 1 2 2 no longer a self-adjoint operator whenever Imf 6= 0). Thus, jf (λ)j δ (λI − T ) dλ = jf (λ)j dEλ: unless otherwise stated, we shall assume that both in (1.1) and −∞ −∞ (1.3) the function f is complex-valued. Note that the complex where the latter equality is the definition of jf (T )j2. So, we Stieltjes measure d hEλx; yi need not be dλ-continuous. In have the following result. what follows we shall denote by Bp (R) the linear space over C consisting of all complex-valued Borel-measurable functions Proposition 2. If T is self-adjoint and f 2 Bp (R), then of one real variable which are continuous on σp (T ). 1 + 1 If fn ! f in D (R), the sequence ffngn=1 is uniformly Z hf (T ) y; f (T ) xi = jf (λ)j2 hy; δ (λI − T ) xi dλ bounded and fn (x) ! f (x) at each x 2 . So, if T is R −∞ bounded on H (equivalently, self-adjoint on the whole of H) it turns out that fn (T ) ! f (T ) in the strong operator topol- for every x; y 2 D (f (T )). ogy [3, 10.2.8 Corollary]. Therefore, in this case δ (λI − T ) is an L (H)-valued distribution. Proof. We adapt a classic argument. Indeed, for every x; y 2 As all integrals considered so far are over σ (T ), we have D (f (T )) we have Z + 1 δ (λI − T ) = 0 8λ2 = σ (T ) : (1.4) hf (T ) y; f (T ) xi = f (λ) d hf (T ) y; Eλxi : −∞ Also δ (−λI + T ) = δ (λI − T ) for all λ 2 . On the other R E E = E µ ≤ λ hE y; xi hand, if µ 2 σ (T ) and y is an eigenvector corresponding to Since µ λ µ whenever , and λ does not p µ the eigenvalue µ, clearly depend on , by splitting the integral we get Z + 1 Z λ δ (λI − T ) y = δ (λ − µ) y (1.5) f (µ) d hEµy; Eλxi = f (µ) d hy; Eµxi ; (1.8) −∞ −∞ for every λ 2 R. In the particular case when Ta is the linear where clearly the first integral is hf (T ) y; Eλxi. Plugging operator defined on H by Tax = ax for a fixed a 2 R, then Ta d hf (T ) y; Eλxi into (1.8), we are done. is a self-adjoint linear operator with σ (Ta) = σp (Ta) = fag. In this case δ (λI − Ta) x = δ (λ − a) x for every x 2 H, i. e., Corollary 3. Under the same conditions of the previous theo- δ (λI − Ta) = δ (λ − a) I. rem, the equality D E Since equality f (T )y y; x = hy; f (T ) xi holds for all Z + 1 2 2 x; y 2 D (f (T )) and each f 2 Bp (R), we may infer that kf (T ) xk = jf (λ)j hx; δ (λI − T ) xi dλ (1.9) −∞ hy; δ (λI − T ) xi = hδ (λI − T ) y; xi holds for every x 2 D (f (T )).
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Or Continuous Spectrum and Not to the Line Spectra. in the X-Ray Region, In
    662 PHYSICS: W. D UA NE PROC. N. A. S. intensity is greatest close to -80 and that it falls off regularly as the angle departs therefrom. We conclude, therefore, that the momentum of the electron in its orbit uithin the atom does not affect the direction of ejection in the way denanded by the theory of Auger and Perrin. While this does not constitute definite evidence against the physical reality of electronic orbits, it is a serious difficulty for the conception. A detailed discussion of the general question here raised in the light of new experimental results will be published elsewhere. 1 Auger, P., J. Physique Rad., 8, 1927 (85-92). 2 Loughridge, D. H., in press. 3 Bothe, W., Zs. Physik, 26, 1924 (59-73). 4 Auger, P., and Perrin, F., J. Physique Rad., 8, 1927 (93-111). 6 Bothe, W., Zs. Physik, 26,1924 (74-84). 6 Watson, E. C., in press. THE CHARACTER OF THE GENERAL, OR CONTINUOUS SPEC- TRUM RADIA TION By WILLIAM DuANX, DJPARTMSNT OF PHysIcs, HARVARD UNIVERSITY Communicated August 6, 1927 The impacts of electrons against atoms produce two different kinds of radiation-the general, or continuous spectrum and the line spectra. By far the greatest amount of energy radiated belongs to the general, or continuous spectrum and not to the line spectra. In the X-ray region, in particular, the continuous, or general radiation spectrum carries most of the radiated energy. In spite of this, and because the line spectra have an important bearing on atomic structure, the general radiation has received much less attention than the line spectra in the recent de- velopment of fundamental ideas in physical science.
    [Show full text]
  • Discrete-Continuous and Classical-Quantum
    Under consideration for publication in Math. Struct. in Comp. Science Discrete-continuous and classical-quantum T. Paul C.N.R.S., D.M.A., Ecole Normale Sup´erieure Received 21 November 2006 Abstract A discussion concerning the opposition between discretness and continuum in quantum mechanics is presented. In particular this duality is shown to be present not only in the early days of the theory, but remains actual, featuring different aspects of discretization. In particular discreteness of quantum mechanics is a key-stone for quantum information and quantum computation. A conclusion involving a concept of completeness linking dis- creteness and continuum is proposed. 1. Discrete-continuous in the old quantum theory Discretness is obviously a fundamental aspect of Quantum Mechanics. When you send white light, that is a continuous spectrum of colors, on a mono-atomic gas, you get back precise line spectra and only Quantum Mechanics can explain this phenomenon. In fact the birth of quantum physics involves more discretization than discretness : in the famous Max Planck’s paper of 1900, and even more explicitly in the 1905 paper by Einstein about the photo-electric effect, what is really done is what a computer does: an integral is replaced by a discrete sum. And the discretization length is given by the Planck’s constant. This idea will be later on applied by Niels Bohr during the years 1910’s to the atomic model. Already one has to notice that during that time another form of discretization had appeared : the atomic model. It is astonishing to notice how long it took to accept the atomic hypothesis (Perrin 1905).
    [Show full text]
  • Spectrum (Functional Analysis) - Wikipedia, the Free Encyclopedia
    Spectrum (functional analysis) - Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/Spectrum_(functional_analysis) Spectrum (functional analysis) From Wikipedia, the free encyclopedia In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the identity operator. The study of spectra and related properties is known as spectral theory, which has numerous applications, most notably the mathematical formulation of quantum mechanics. The spectrum of an operator on a finite-dimensional vector space is precisely the set of eigenvalues. However an operator on an infinite-dimensional space may have additional elements in its spectrum, and may have no eigenvalues. For example, consider the right shift operator R on the Hilbert space ℓ2, This has no eigenvalues, since if Rx=λx then by expanding this expression we see that x1=0, x2=0, etc. On the other hand 0 is in the spectrum because the operator R − 0 (i.e. R itself) is not invertible: it is not surjective since any vector with non-zero first component is not in its range. In fact every bounded linear operator on a complex Banach space must have a non-empty spectrum. The notion of spectrum extends to densely-defined unbounded operators. In this case a complex number λ is said to be in the spectrum of such an operator T:D→X (where D is dense in X) if there is no bounded inverse (λI − T)−1:X→D.
    [Show full text]
  • Continuous Spectrum—Kirchoff's First
    Continuous Spectrum—Kirchoff’s First Law • A hot opaque substance (solid, liquid or gas) gives off a continuous spectrum, that is, a spectrum containing energy at all wavelengths. • Examples where a continuous spectrum will be found: • An incandescent bulb. • A pool of molten iron • Lava flowing from a volcano. • A hot, ionized, opaque gas (such as below the Sun’s atmosphere). • A continuous spectrum approximates a black body spectrum, the spectrum observed from a perfectly black substance heated to a high temperature. No real spectrum is a perfect black body spectrum, but many are good approximations to it. AST 303: Chapter 13 1 Black-body (Continuous) Spectrum • The energy distribution of a black body spectrum looks like this: 1000 Visible 100 10 UV Infrared Intensity (arbitrary units) 1 1000 3000 10000 30000 100000 Wavelength (Ångstroms) AST 303: Chapter 13 2 Wien’s Law—Temperature Dependence (1) • We are familiar with the fact that the color of a heated object changes as its temperature changes. As we heat a substance, it first glows a dull red; then a bright red, then orange, yellow, white, and finally bluish-white. This happens because the distribution of energy with wavelength shifts to predominantly shorter and shorter wavelengths as the temperature rises. • Mathematically, we can calculate the wavelength of maximum emission: 3 !107 Wavelength of Maximum = Å T where T is the temperature in degrees Kelvin. AST 303: Chapter 13 3 How Color Varies with Temperature AST 303: Chapter 13 4 Emission Spectra—Kirchoff’s Second Law • When a transparent gas is heated to a high temperature, one sees an emission spectrum, also known as a bright-line spectrum.
    [Show full text]
  • Continuous Spectrum X-Rays from Thin Targets
    RP 60 CONTINUOUS SPECTRUM X RAYS FROM THIN TARGETS * By Warren W. Nicholas 2 Technique is described for the use of thin metal foils as anticathodes in X-ray- tubes. The continuous radiation from these foils is analyzed by a crystal, the intensities being measured by a photographic comparison method. It is indicated that the high-frequency limit of the continuous spectrum from an infinitely thin target consists of a finite discontinuity. (The corresponding thick target spectrum has only a discontinuity of slope.) The energy distributions on a frequency scale are approximately horizontal, for gold and for aluminum, and for ^=40°, 90°, and 140°, where \I/ is the angle between measured X rays and cathode stream; this agrees with Kramer's, but not with Wentzel's, theory. The intensities for these values of \p are roughly 3:2:1, respectively; theories have not yet been constructed for the variation with \p of resolved energy, but it is pointed out that the observations do not support a supposed quantum process in which a single cathode ray, losing energy hv by interaction with a nucleus, radiates a single frequency v in the continuous spectrum. The observations do not support the "absorption" process assumed by Lenard, in which cathode rays, in penetrating a metal, suffered large losses of speed not accompanied by radiation. The manner in which thick target spectra are synthesized from thin is discussed, and empirical laws are formulated describing the dependence on of thick target continuous spectrum energy. A structure for the moving \f/ electron is proposed which explains classically X ray continuous spectrum phenomena, and seems to have application in other fields as well.
    [Show full text]
  • X-Ray Emission Spectrum
    X-ray Emission Spectrum Dr. Ahmed Alsharef Farah Dr. Ahmed Alsharef Farah 1 • X-ray photons produced by an X-ray tube are heterogeneous in energy. • The energy spectrum shows a continuous distribution of energies for the bremsstrahlung photons superimposed by characteristic radiation of discrete energies. Dr. Ahmed Alsharef Farah 2 There are two types of X-ray spectrum: 1. Bremsstrahlung or continuous spectrum. 2. Characteristic spectrum. Dr. Ahmed Alsharef Farah 3 • A bremsstrahlung spectrum consists of X- ray photons of all energies up to maximum in a continuous fashion, which is also known as white radiation, because of its similarity to white light. • A characteristic spectrum consists of X-ray photons of few energy, which is also called as line spectrum. • The position of the characteristic radiation depends upon the atomic number of the target. Dr. Ahmed Alsharef Farah 4 Dr. Ahmed Alsharef Farah 5 Characteristic X-ray Spectrum: • The discrete energies of characteristic x- rays are characteristic of the differences between electron binding energies in a particular element. • A characteristic x-ray from tungsten, for example, can have 1 of 15 different energies and no others. Dr. Ahmed Alsharef Farah 6 Characteristic X-rays of Tungsten and Their Effective Energies (keV). Dr. Ahmed Alsharef Farah 7 Characteristic x-ray emission spectrum for tungsten contains 15 different x-ray energies. Dr. Ahmed Alsharef Farah 8 • Such a plot is called the characteristic x-ray emission spectrum. • Five vertical lines representing K x-rays and four vertical lines representing L x-rays are included. • The lower energy lines represent characteristic emissions from the outer electron shells.
    [Show full text]
  • Flexible Learning Approach to Physics (FLAP)
    ATOMIC SPECTRA AND THE HYDROGEN ATOM MODULE P8.2 F PAGE P8.2.1 Module P8.2 Atomic spectra and the hydrogen atom 1 Opening items 1 Ready to study? 2 The production of atomic spectra 3 Study comment To study this module you will need to understand the following terms: 2.1 Characteristic emission spectra 3 absolute temperature, angular momentum, angular frequency, atom, Boltzmann’s constant, 2.2 Continuous emission spectra; the centripetal force, circular motion, Coulomb’s law, diffraction grating, dispersion, electric black-body spectrum 4 potential energy, electromagnetic radiation, electromagnetic spectrum (including ultraviolet 2.3 Absorption spectra 4 and infrared), electronvolt, energy conservation, force, frequency the grating relation 2.4 Summary of Section 2 5 λ2 2 1 1θ (n = d sin n), kinetic energy, molecule momentum, momentum conservation, Newton’s 3 The emission spectrum of laws of motion, orders of diffraction, wavelength. In addition, some familiarity with the use atomic hydrogen 5 of basic algebra, exponentials, graph plotting, logarithms and trigonometric functions will 3.1 The visible spectrum of atomic be assumed. If you are uncertain about any of these terms, review them now by reference to hydrogen; Balmer’s formula 6 the Glossary, which will also indicate where in FLAP they are developed. 3.2 The ultraviolet and infrared series of lines for hydrogen 6 Module summary 3.3 Summary of Section 3 7 1 The spectrum of a sample of electromagnetic radiation shows the way in which 4 Bohr’s model for the hydrogen atom 7 the energy carried by that radiation is distributed with respect to wavelength 4.1 The four postulates 7 (or frequency).
    [Show full text]
  • Electromagnetic Radiation Production of Light
    Electromagnetic Radiation Production of Light Full window version (looks a little nicer). Click <Back> button to get back to small framed version with content indexes. This material (and images) is copyrighted!. See my copyright notice for fair use practices. When light is passed through a prism or a diffraction grating to produce a spectrum, the type of spectrum you will see depends on what kind of object is producing the light: is it a thick or thin gas, is it hot or cool, is it a gas or a solid? There are two basic types of spectra: continuous spectrum (energy at all wavelengths) and discrete spectrum (energy at only certain wavelengths). Astronomers usually refer to the two types of discrete spectra: emission lines (bright lines) and absorption lines (dark lines in an otherwise continuous spectrum) as different types of spectra. Continuous Spectrum A rainbow is an example of a continuous spectrum. Most continuous spectra are from hot, dense objects like stars, planets, or moons. The continuous spectrum from these kinds of objects is also called a thermal spectrum, because hot, dense objects will emit electromagnetic radiation at all wavelengths or colors. Any solid, liquid and dense (thick) gas at a temperature above absolute zero will produce a thermal spectrum. A thermal spectrum is the simplest type of spectrum because its shape depends on only the temperature. A discrete spectrum is more complex because it depends on temperature and other things like the chemical composition of the object, the gas density, surface gravity, speed, etc. Exotic objects like neutron stars and black holes can produce another type of continuous spectrum called ``synchrotron spectrum'' from charged particles swirling around magnetic fields, but I will discuss them in another chapter later on.
    [Show full text]
  • Characteristic and Continuous X-Rays Jitender Singh| October 18, 2019
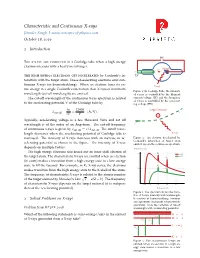
    Characteristic and Continuous X-rays Jitender Singh| www.concepts-of-physics.com October 18, 2019 1 Introduction HV • • The x-rays are produced in a Coolidge tube when a high energy −+ electron interacts with a heavy metal target. Anode e− +−• Cathode • The high energy electrons get decelerated by Coulomb’s in- LV teraction with the target atom. These decelerating electrons emit con- tinuous X-rays (or bremsstrahlung). When an electron loses its en- X-ray tire energy in a single Coulomb’s interaction then X-rays of minimum Figure 1: In Coolidge Tube, the intensity wavelength (cut-off wavelength) are emitted. of x-rays is controlled by the filament The cut-off wavelength of the continuous X-ray spectrum is related current/voltage (LV) and the frequency of x-rays is controlled by the accelerat- to the accelerating potential V of the Coolidge tube by ing voltage (HV). hc 12400 Target Nucleus • − lcut off = ≈ (Å/V). e eV V + Typically, accelerating voltage is a few thousand Volts and cut off • − wavelength is of the order of an Angstrom. The cut-off frequency e of continuous x-rays is given by ncut off = c/lcut off. The cutoff wave- length decreases when the accelerating potential of Coolidge tube is X-ray increased. The intensity of X-rays increases with an increase in ac- Figure 2: An electron decelerated by Coulomb’s interaction of target atom celerating potential as shown in the figure. The intensity of X-rays emits X-rays in the continuous spectrum. depends on multiple factors. Relative Intensity The high energy electrons also knock out an inner shell electron of 1.0 K a 50 kV the target atom.
    [Show full text]
  • The Spectrum of Atomic Hydrogen
    The Spectrum of Atomic Hydrogen For almost a century light emitted by the simplest of atoms has been the chief experimental basis for theories of the structure of matter. Exploration of the hydrogen spectrum continues, now aided by lasers by Theodor W. Hansch, Arthur L. Schawlow and George W. Series he spectrum of the hydrogen atom sorbed. glvmg rise to dark lines on a that he could account for the positions has proved to be the Rosetta stone bright background. of all the known lines by applying a sim­ Tof modern physics: once this pat­ Hydrogen is the simplest of atoms. be­ ple empirical formula. The entire set of tern of lines had been deciphered much ing made up of a single electron and a lines has since come to be known as the else could also be understood. Most no­ nucleus that consists of a single proton. Balmer series. Another group of lines. tably. it was largely the effort to explain and so it can be expected to have the the Lyman series. lies in the far ultravio­ the spectrum of light emitted by the hy­ simplest spectrum. The spectrum is not. let. and there are other series at longer drogen atom that inspired the laws of however. an easy one to record. The wavelengths. Within each series the in­ quantum mechanics. Those laws have most prominent line was detected in dividual lines are designated by Greek since been found to apply not only to 1853 by Anders Jonas Angstrom. (The letters. starting with the line of longest the hydrogen atom but also to other common unit for measuring wave­ wavelength.
    [Show full text]
  • The Formalism of Quantum Mechanics Relevant Sections in Text
    The formalism of quantum mechanics The formalism of quantum mechanics Relevant sections in text: Chapter 3 Now for some formalism::: We have now acquired a little familiarity with how quantum mechanics works via some simple examples. Our approach has been rather informal; we have not clearly stated the rules of the game. The situation is analogous to one way of studying Newtonian mechanics. In your first exposure to Newtonian mechanics you may have had the following experience. First, we introduce some basic concepts, such as vectors, force, acceleration, energy, etc. We learn, to some extent, how to use these concepts by studying some simple examples. Along the way, we state (perhaps without full generality) some of the key laws that are being used. Second, we make things a bit more systematic, e.g., by carefully stating Newton's laws. More or less, we have completed the first of the steps. Now we must complete the second step. To formulate the laws (or postulates) of quantum mechanics, we need to spend a little time giving some mathematical method to the madness we have been indulging in so far. In particular, we need to give a linear algebraic type of interpretation to the apparatus of wave functions, operators, expectation values, and so forth. We begin by developing a point of view in which states of the system are elements of a (very large) vector space. I assume that you are already familiar with the fundamentals of linear algebra (vector spaces, bases, linear transformations, eigenvalue problems, etc. ). If you need some remedial work, have a look at the first section of chapter 3 in the text.
    [Show full text]