DOCSLIB.ORG

Polyhedra VEF

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Polyhedra VEF Polyhedra KEY Polyhedra (Polyhedron, singular) are 3-D objects with faces that are polygons. Doing math is just like paradise. ☺ (F) Faces are the flat smooth surfaces. The faces are 2-D polygons. (E) Edges are where two faces meet. (V) Vertices are the “points” where edges meet. NOTE: Remember to keep the vocabulary straight for our formulas! For example, a “six-sided die” is considered to be a cube with 6 faces , NOT 6 sides! We will now introduce a new vocabulary phrase “ sides of faces ”. This is different from a “Face” or from an “Edge”. When viewing a polygon face, think of it as a 2-D object. Therefore, we can view the sides of the polygon as “sides of faces”. “Side of a face” is different than an “Edge” since an “Edge” is a 3-D label. In fact, each “Edge” is composed of two “sides of faces” because each edge is where two faces meet. If we go around a polyhedron and count the total number of “sides of faces” from all of its polygon faces, then we have in fact counted all of the edges of the polyhedron twice! This gives us the following formula: Total Sides of Faces = 2E . Together with Euler’s famous formula for polyhedra, V – E + F = 2 , we are able to determine the number of edges and vertices of any polyhedron just by knowing the number and type of polygon faces that it has. NOTE: we consider only convex polyhedra. 1 Polyhedra KEY Total Sides of Faces = 2E V – E + F = 2 1. A cube has six faces which are all squares. How many edges and vertices does it have? type of face Square # of each face 6 # of sides per face 4 total sides of faces 24 Total Sides of Faces 2E 24 2E 12 E V – E F 2 V – 12 6 2 V – 6 2 V 8 A cube has 12 edges and 8 vertices. 2. Dice are often used in gaming such as the role-playing game Dungeons & Dragons . The 20- sided die is a type of polyhedron called an icosahedron. It has 20 faces all of which are equilateral triangles. How many edges and vertices does an icosahedron have? type of face Triangle # of each face 20 # of sides per face 3 total sides of faces 60 Total Sides of Faces 2E 60 2E 30 E V – E F 2 V – 30 20 2 V – 10 2 V 12 An icosahedron has 30 edges and 12 vertices. 2 Polyhedra KEY 3. Suppose a convex polyhedron has 11 faces, of which 4 are triangles, 5 are quadrilaterals, and 2 are hexagons. How many vertices and edges does it have? type of face Triangle Quadrilateral Hexagon # of each face 4 5 2 # of sides per face 3 4 6 total sides of faces 12 20 12 Total Sides of Faces 2E 122012 2E 44 2E 22 E V – E F 2 V – 22 11 2 V – 11 2 V 13 The convex polyhedron has 22 edges and 13 vertices. 3 Polyhedra KEY 4. The cuboctahedron is a polyhedron that can be constructed by slicing off the corners of a cube through the midpoints of the edges as shown below. a. How many triangle faces does a cuboctahedron have? The cuboctahedron has one triangle face for each vertex from the previous cube. Since the cube has 8 vertices (see question #1) then it follows that the cuboctahedron has 8 triangle faces. b. How many square faces does a cuboctahedron have? The cuboctahedron has one square face for each left-over face from the previous cube. Since the cube has 6 faces (see question #1) then it follows that the cuboctahedron has 6 square faces. c. How many edges and vertices does a cuboctahedron have? type of face Triangle Square # of each face 8 6 # of sides per face 3 4 total sides of faces 24 24 Total Sides of Faces 2E 24 24 2E 48 2E 24 E NOTE: F 8 6 14 V – E F 2 V – 24 14 2 V – 10 2 V 12 The cuboctahedron has 24 edges and 12 vertices. 4 Polyhedra KEY ADDITIONAL EXERCISES 5. A “net” for a polyhedron is a squashed version that shows, in a 2-D way, how the polygon faces are connected to each other. In fact, if you were to cut out the net image from this piece of paper, you could fold it back up into the 3-D polyhedron! To the right is the net for the Pentagonal Rotunda. You can see that it has 17 faces, of which 6 are pentagons, 10 are triangles, and 1 is a decagon. How many edges and vertices does it have? type of face Pentagon Triangle Decagon # of each face 6 10 1 # of sides per face 5 3 10 total sides of faces 30 30 10 Total Sides of Faces 2E 30 30 10 2E 70 2E 35 E V – E F 2 V – 35 17 2 V – 18 2 V 20 The Pentagonal Rotunda has 35 edges and 20 vertices. 5 Polyhedra KEY 6. Below is the net and image for the Augmented Dodecahedron. How many edges and vertices does it have? type of face Pentagon Triangle # of each face 11 5 # of sides per face 5 3 total sides of faces 55 15 Total Sides of Faces 2E 55 15 2E 70 2E 35 E NOTE: F 11 5 16 V – E F 2 V – 35 16 2 V – 19 2 V 21 The Augmented Dodecahedron has 35 edges and 21 vertices. 6 Polyhedra KEY 7. Below is the net for the Pentagonal Orthocupolarontunda. How many edges and vertices does it have? type of face Triangle Square Pentagon # of each face 15 5 7 # of sides per face 3 4 5 total sides of faces 45 20 35 Total Sides of Faces 2E 45 20 35 2E 100 2E 50 E NOTE: F 15 5 7 27 V – E F 2 V – 50 27 2 V – 23 2 V 25 The Pentagonal Orthocupolarontunda has 50 edges and 25 vertices. 7 Polyhedra KEY 8. Below is the net and image for the Hexagonal Antiprism. How many edges and vertices does it have? type of face Triangle Hexagon # of each face 12 2 # of sides per face 3 6 total sides of faces 36 12 Total Sides of Faces 2E 36 12 2E 48 2E 24 E NOTE: F 12 2 14 V – E F 2 V – 24 14 2 V – 10 2 V 12 The Hexagonal Antiprism has 24 edges and 12 vertices. 8 Polyhedra KEY 9. The 8-sided die is a type of polyhedron called an octahedron. It is a polyhedron with eight triangle faces. How many vertices and edges does it have? type of face Triangle # of each face 8 # of sides per face 3 total sides of faces 24 Total Sides of Faces 2E 24 2E 12 E V – E F 2 V – 12 8 2 V – 4 2 V 6 An octahedron has 12 edges and 6 vertices. 9 Polyhedra KEY 10. The truncated octahedron can be constructed by slicing off the corners of an octahedron so that a square is formed. a. How many square faces does a truncated octahedron have? The truncated octahedron has one square face for each vertex from the original octahedron. Since an octahedron has 6 vertices (see question #9) then it follows that the truncated octahedron has 6 square faces. b. How many hexagon faces does a truncated octahedron have? The truncated octahedron has one hexagon face for each left-over face from the original octahedron. Since an octahedron has 8 faces (see question #9) then it follows that the truncated octahedron has 8 hexagon faces. c. How many edges and vertices does a truncated octahedron have? type of face Square Hexagon # of each face 6 8 # of sides per face 4 6 total sides of faces 24 48 Total Sides of Faces 2E 24 48 2E 72 2E 36 E NOTE: F 6 8 14 V – E F 2 V – 36 14 2 V – 22 2 V 24 The truncated octahedron has 36 edges and 24 vertices. 10 Polyhedra KEY 11. The truncated icosahedron can be constructed by slicing off the corners of an icosahedron so that a pentagon is formed. a. How many pentagon faces does the truncated icosahedron have? The truncated icosahedron has one pentagon face for each vertex from the original icosahedron. Since an icosahedron has 12 vertices (see question #2) then it follows that the truncated icosahedron has 12 pentagon faces. b. How many hexagon faces does the truncated icosahedron have? The truncated icosahedron has one hexagon face for each left-over face from the original icosahedron. Since an icosahedron has 20 faces (see question #2) then it follows that the truncated icosahedron has 20 hexagon faces. c. How many edges and vertices does the truncated icosahedron have? type of face Pentagon Hexagon # of each face 12 20 # of sides per face 5 6 total sides of faces 60 120 Total Sides of Faces 2E 60 120 2E 180 2E 90 E NOTE: F 12 20 32 V – E F 2 V – 90 32 2 V – 58 2 V 60 The truncated icosahedron has 90 edges and 60 vertices. 11 Polyhedra KEY 12. The Trapezoidal Hexecontahedron is a polyhedron with 60 quadrilateral faces. How many vertices and edges does it have? type of face Quadrilateral # of each face 60 # of sides per face 4 total sides of faces 240 Total Sides of Faces 2E 240 2E 120 E V – E F 2 V – 120 60 2 V – 60 2 V 62 The Trapezoidal Hexecontahedron has 120 edges and 62 vertices.
Load more

Recommended publications
  • Lecture 3 1 Geometry of Linear Programs
    ORIE 6300 Mathematical Programming I September 2, 2014 Lecture 3 Lecturer: David P. Williamson Scribe: Divya Singhvi Last time we discussed how to take dual of an LP in two different ways. Today we will talk about the geometry of linear programs. 1 Geometry of Linear Programs First we need some definitions. Definition 1 A set S ⊆ <n is convex if 8x; y 2 S, λx + (1 − λ)y 2 S, 8λ 2 [0; 1]. Figure 1: Examples of convex and non convex sets Given a set of inequalities we define the feasible region as P = fx 2 <n : Ax ≤ bg. We say that P is a polyhedron. Which points on this figure can have the optimal value? Our intuition from last time is that Figure 2: Example of a polyhedron. \Circled" corners are feasible and \squared" are non feasible optimal solutions to linear programming problems occur at \corners" of the feasible region. What we'd like to do now is to consider formal definitions of the \corners" of the feasible region. 3-1 One idea is that a point in the polyhedron is a corner if there is some objective function that is minimized there uniquely. Definition 2 x 2 P is a vertex of P if 9c 2 <n with cT x < cT y; 8y 6= x; y 2 P . Another idea is that a point x 2 P is a corner if there are no small perturbations of x that are in P . Definition 3 Let P be a convex set in <n. Then x 2 P is an extreme point of P if x cannot be written as λy + (1 − λ)z for y; z 2 P , y; z 6= x, 0 ≤ λ ≤ 1.
    [Show full text]
  • Snub Cell Tetricosa
    E COLE NORMALE SUPERIEURE ________________________ A Zo o of ` embeddable Polytopal Graphs Michel DEZA VP GRISHUHKIN LIENS ________________________ Département de Mathématiques et Informatique CNRS URA 1327 A Zo o of ` embeddable Polytopal Graphs Michel DEZA VP GRISHUHKIN LIENS January Lab oratoire dInformatique de lEcole Normale Superieure rue dUlm PARIS Cedex Tel Adresse electronique dmiensfr CEMI Russian Academy of Sciences Moscow A zo o of l embeddable p olytopal graphs MDeza CNRS Ecole Normale Superieure Paris VPGrishukhin CEMI Russian Academy of Sciences Moscow Abstract A simple graph G V E is called l graph if for some n 2 IN there 1 exists a vertexaddressing of each vertex v of G by a vertex av of the n cub e H preserving up to the scale the graph distance ie d v v n G d av av for all v 2 V We distinguish l graphs b etween skeletons H 1 n of a variety of well known classes of p olytop es semiregular regularfaced zonotop es Delaunay p olytop es of dimension and several generalizations of prisms and antiprisms Introduction Some notation and prop erties of p olytopal graphs and hypermetrics Vector representations of l metrics and hypermetrics 1 Regularfaced p olytop es Regular p olytop es Semiregular not regular p olytop es Regularfaced not semiregularp olytop es of dimension Prismatic graphs Moscow and Glob e graphs Stellated k gons Cup olas Antiwebs Capp ed antiprisms towers and fullerenes regularfaced not semiregular p olyhedra Zonotop es Delaunay p olytop es Small
    [Show full text]
  • Equivelar Octahedron of Genus 3 in 3-Space
    Equivelar octahedron of genus 3 in 3-space Ruslan Mizhaev ([email protected]) Apr. 2020 ABSTRACT . Building up a toroidal polyhedron of genus 3, consisting of 8 nine-sided faces, is given. From the point of view of topology, a polyhedron can be considered as an embedding of a cubic graph with 24 vertices and 36 edges in a surface of genus 3. This polyhedron is a contender for the maximal genus among octahedrons in 3-space. 1. Introduction This solution can be attributed to the problem of determining the maximal genus of polyhedra with the number of faces - . As is known, at least 7 faces are required for a polyhedron of genus = 1 . For cases ≥ 8 , there are currently few examples. If all faces of the toroidal polyhedron are – gons and all vertices are q-valence ( ≥ 3), such polyhedral are called either locally regular or simply equivelar [1]. The characteristics of polyhedra are abbreviated as , ; [1]. 2. Polyhedron {9, 3; 3} V1. The paper considers building up a polyhedron 9, 3; 3 in 3-space. The faces of a polyhedron are non- convex flat 9-gons without self-intersections. The polyhedron is symmetric when rotated through 1804 around the axis (Fig. 3). One of the features of this polyhedron is that any face has two pairs with which it borders two edges. The polyhedron also has a ratio of angles and faces - = − 1. To describe polyhedra with similar characteristics ( = − 1) we use the Euler formula − + = = 2 − 2, where is the Euler characteristic. Since = 3, the equality 3 = 2 holds true.
    [Show full text]
  • The Continuum of Space Architecture: from Earth to Orbit
    42nd International Conference on Environmental Systems AIAA 2012-3575 15 - 19 July 2012, San Diego, California The Continuum of Space Architecture: From Earth to Orbit Marc M. Cohen1 Marc M. Cohen Architect P.C. – Astrotecture™, Palo Alto, CA, 94306 Space architects and engineers alike tend to see spacecraft and space habitat design as an entirely new departure, disconnected from the Earth. However, at least for Space Architecture, there is a continuum of development since the earliest formalizations of terrestrial architecture. Moving out from 1-G, Space Architecture enables the continuum from 1-G to other gravity regimes. The history of Architecture on Earth involves finding new ways to resist Gravity with non-orthogonal structures. Space Architecture represents a new milestone in this progression, in which gravity is reduced or altogether absent from the habitable environment. I. Introduction EOMETRY is Truth2. Gravity is the constant.3 Gravity G is the constant – perhaps the only constant – in the evolution of life on Earth and the human response to the Earth’s environment.4 The Continuum of Architecture arises from geometry in building as a primary human response to gravity. It leads to the development of fundamental components of construction on Earth: Column, Wall, Floor, and Roof. According to the theoretician Abbe Laugier, the column developed from trees; the column engendered the wall, as shown in FIGURE 1 his famous illustration of “The Primitive Hut.” The column aligns with the human bipedal posture, where the spine, pelvis, and legs are the gravity- resisting structure. Caryatids are the highly literal interpretation of this phenomenon of standing to resist gravity, shown in FIGURE 2.
    [Show full text]
  • Composite Concave Cupolae As Geometric and Architectural Forms
    Journal for Geometry and Graphics Volume 19 (2015), No. 1, 79–91. Composite Concave Cupolae as Geometric and Architectural Forms Slobodan Mišić1, Marija Obradović1, Gordana Ðukanović2 1Faculty of Civil Engineering, University of Belgrade Bulevar kralja Aleksandra 73, 11000 Belgrade, Serbia emails: [email protected], [email protected] 2Faculty of Forestry, University of Belgrade, Serbia email: [email protected] Abstract. In this paper, the geometry of concave cupolae has been the starting point for the generation of composite polyhedral structures, usable as formative patterns for architectural purposes. Obtained by linking paper folding geometry with the geometry of polyhedra, concave cupolae are polyhedra that follow the method of generating cupolae (Johnson’s solids: J3, J4 and J5); but we removed the convexity criterion and omitted squares in the lateral surface. Instead of alter- nating triangles and squares there are now two or more paired series of equilateral triangles. The criterion of face regularity is respected, as well as the criterion of multiple axial symmetry. The distribution of the triangles is based on strictly determined and mathematically defined parameters, which allows the creation of such structures in a way that qualifies them as an autonomous group of polyhedra — concave cupolae of sorts II, IV, VI (2N). If we want to see these structures as polyhedral surfaces (not as solids) connecting the concept of the cupola (dome) in the architectural sense with the geometrical meaning of (concave) cupola, we re- move the faces of the base polygons. Thus we get a deltahedral structure — a shell made entirely from equilateral triangles, which is advantageous for the purpose of prefabrication.
    [Show full text]
  • 1 Lifts of Polytopes
    Lecture 5: Lifts of polytopes and non-negative rank CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Lifts of polytopes 1.1 Polytopes and inequalities Recall that the convex hull of a subset X n is defined by ⊆ conv X λx + 1 λ x0 : x; x0 X; λ 0; 1 : ( ) f ( − ) 2 2 [ ]g A d-dimensional convex polytope P d is the convex hull of a finite set of points in d: ⊆ P conv x1;:::; xk (f g) d for some x1;:::; xk . 2 Every polytope has a dual representation: It is a closed and bounded set defined by a family of linear inequalities P x d : Ax 6 b f 2 g for some matrix A m d. 2 × Let us define a measure of complexity for P: Define γ P to be the smallest number m such that for some C s d ; y s ; A m d ; b m, we have ( ) 2 × 2 2 × 2 P x d : Cx y and Ax 6 b : f 2 g In other words, this is the minimum number of inequalities needed to describe P. If P is full- dimensional, then this is precisely the number of facets of P (a facet is a maximal proper face of P). Thinking of γ P as a measure of complexity makes sense from the point of view of optimization: Interior point( methods) can efficiently optimize linear functions over P (to arbitrary accuracy) in time that is polynomial in γ P . ( ) 1.2 Lifts of polytopes Many simple polytopes require a large number of inequalities to describe.
    [Show full text]
  • Geometry © 2000 Springer-Verlag New York Inc
    Discrete Comput Geom OF1–OF15 (2000) Discrete & Computational DOI: 10.1007/s004540010046 Geometry © 2000 Springer-Verlag New York Inc. Convex and Linear Orientations of Polytopal Graphs J. Mihalisin and V. Klee Department of Mathematics, University of Washington, Box 354350, Seattle, WA 98195-4350, USA {mihalisi,klee}@math.washington.edu Abstract. This paper examines directed graphs related to convex polytopes. For each fixed d-polytope and any acyclic orientation of its graph, we prove there exist both convex and concave functions that induce the given orientation. For each combinatorial class of 3-polytopes, we provide a good characterization of the orientations that are induced by an affine function acting on some member of the class. Introduction A graph is d-polytopal if it is isomorphic to the graph G(P) formed by the vertices and edges of some (convex) d-polytope P. As the term is used here, a digraph is d-polytopal if it is isomorphic to a digraph that results when the graph G(P) of some d-polytope P is oriented by means of some affine function on P. 3-Polytopes and their graphs have been objects of research since the time of Euler. The most important result concerning 3-polytopal graphs is the theorem of Steinitz [SR], [Gr1], asserting that a graph is 3-polytopal if and only if it is planar and 3-connected. Also important is the related fact that the combinatorial type (i.e., the entire face-lattice) of a 3-polytope P is determined by the graph G(P). Steinitz’s theorem has been very useful in studying the combinatorial structure of 3-polytopes because it makes it easy to recognize the 3-polytopality of a graph and to construct graphs that represent 3-polytopes without producing an explicit geometric realization.
    [Show full text]
  • Archimedean Solids
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
    [Show full text]
  • Shape Skeletons Creating Polyhedra with Straws
    Shape Skeletons Creating Polyhedra with Straws Topics: 3-Dimensional Shapes, Regular Solids, Geometry Materials List Drinking straws or stir straws, cut in Use simple materials to investigate regular or advanced 3-dimensional shapes. half Fun to create, these shapes make wonderful showpieces and learning tools! Paperclips to use with the drinking Assembly straws or chenille 1. Choose which shape to construct. Note: the 4-sided tetrahedron, 8-sided stems to use with octahedron, and 20-sided icosahedron have triangular faces and will form sturdier the stir straws skeletal shapes. The 6-sided cube with square faces and the 12-sided Scissors dodecahedron with pentagonal faces will be less sturdy. See the Taking it Appropriate tool for Further section. cutting the wire in the chenille stems, Platonic Solids if used This activity can be used to teach: Common Core Math Tetrahedron Cube Octahedron Dodecahedron Icosahedron Standards: Angles and volume Polyhedron Faces Shape of Face Edges Vertices and measurement Tetrahedron 4 Triangles 6 4 (Measurement & Cube 6 Squares 12 8 Data, Grade 4, 5, 6, & Octahedron 8 Triangles 12 6 7; Grade 5, 3, 4, & 5) Dodecahedron 12 Pentagons 30 20 2-Dimensional and 3- Dimensional Shapes Icosahedron 20 Triangles 30 12 (Geometry, Grades 2- 12) 2. Use the table and images above to construct the selected shape by creating one or Problem Solving and more face shapes and then add straws or join shapes at each of the vertices: Reasoning a. For drinking straws and paperclips: Bend the (Mathematical paperclips so that the 2 loops form a “V” or “L” Practices Grades 2- shape as needed, widen the narrower loop and insert 12) one loop into the end of one straw half, and the other loop into another straw half.
    [Show full text]
  • A Fun Approach to Teaching Geometry and Inspiring Creativity
    Proceedings of Bridges 2013: Mathematics, Music, Art, Architecture, Culture A Fun Approach to Teaching Geometry and Inspiring Creativity Ioana Browne, Michael Browne, Mircea Draghicescu*, Cristina Draghicescu, Carmen Ionescu ITSPHUN LLC 2023 NW Lovejoy St. Portland, OR 97209, USA [email protected] Abstract ITSPHUNTM geometric shapes can be easily combined to create an infinite number of structures both decorative and functional. We introduce this system of shapes, and discuss its use for teaching mathematics. At the workshop, we will provide a large number of pieces of various shapes, demonstrate their use, and give all participants the opportunity to build their own creations at the intersection of art and mathematics. Introduction Connecting pieces of paper by sliding them together along slits or cuts is a well-known method of building 3D objects ([2], [3], [4]). Based on this idea we developed a system of shapes1 that can be used to build arbitrarily complex structures. Among the geometric objects that can be built are Platonic, Archimedean, and Johnson solids, prisms and antiprisms, many nonconvex polyhedra, several space-filling tessellations, etc. Guided by an user’s imagination and creativity, simple objects can then be connected to form more complex constructs. ITSPHUN pieces made of various materials2 can be used for creative play, for making functional and decorative objects such as jewelry, lamps, furniture, and, in classroom, for teaching mathematical concepts.3 1Patent pending. 2We used many kinds of paper, cardboard, foam, several kinds of plastic, wood and plywood, wood veneer, fabric, and felt. 3In addition to models of geometric objects, ITSPHUN shapes have been used to make birds, animals, flowers, trees, houses, hats, glasses, and much more - see a few examples in the photo gallery at www.itsphun.com.
    [Show full text]
  • Digital Geometry Processing Mesh Basics
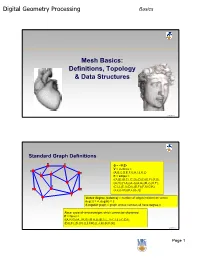
    Digital Geometry Processing Basics Mesh Basics: Definitions, Topology & Data Structures 1 © Alla Sheffer Standard Graph Definitions G = <V,E> V = vertices = {A,B,C,D,E,F,G,H,I,J,K,L} E = edges = {(A,B),(B,C),(C,D),(D,E),(E,F),(F,G), (G,H),(H,A),(A,J),(A,G),(B,J),(K,F), (C,L),(C,I),(D,I),(D,F),(F,I),(G,K), (J,L),(J,K),(K,L),(L,I)} Vertex degree (valence) = number of edges incident on vertex deg(J) = 4, deg(H) = 2 k-regular graph = graph whose vertices all have degree k Face: cycle of vertices/edges which cannot be shortened F = faces = {(A,H,G),(A,J,K,G),(B,A,J),(B,C,L,J),(C,I,L),(C,D,I), (D,E,F),(D,I,F),(L,I,F,K),(L,J,K),(K,F,G)} © Alla Sheffer Page 1 Digital Geometry Processing Basics Connectivity Graph is connected if there is a path of edges connecting every two vertices Graph is k-connected if between every two vertices there are k edge-disjoint paths Graph G’=<V’,E’> is a subgraph of graph G=<V,E> if V’ is a subset of V and E’ is the subset of E incident on V’ Connected component of a graph: maximal connected subgraph Subset V’ of V is an independent set in G if the subgraph it induces does not contain any edges of E © Alla Sheffer Graph Embedding Graph is embedded in Rd if each vertex is assigned a position in Rd Embedding in R2 Embedding in R3 © Alla Sheffer Page 2 Digital Geometry Processing Basics Planar Graphs Planar Graph Plane Graph Planar graph: graph whose vertices and edges can Straight Line Plane Graph be embedded in R2 such that its edges do not intersect Every planar graph can be drawn as a straight-line plane graph ©
    [Show full text]
  • Sonobe Assembly Guide for a Few Polyhedra
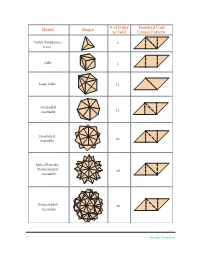
    Model Shape # of Units Finished Unit to Fold Crease Pattern Toshie Takahama’s 3 Jewel Cube 6 Large Cube 12 Octahedral Assembly 12 Icosahedral Assembly 30 Spiked Pentakis Dodecahedral 60 Assembly Dodecahedral 90 Assembly 2 Sonobe Variations Sonobe Assembly Basics Sonobe assemblies are essentially “pyramidized” constructing a polyhedron, the key thing to re- polyhedra, each pyramid consisting of three So- member is that the diagonal ab of each Sonobe nobe units. The figure below shows a generic So- unit will lie along an edge of the polyhedron. nobe unit and how to form one pyramid. When a Pocket Tab Forming one Tab pyramid Pocket b A generic Sonobe unit representation Sonobe Assembly Guide for a Few Polyhedra 1. Toshie’s Jewel: Crease three finished units as tabs and pockets. This assembly is also sometimes explained in the table on page 2. Form a pyramid known as a Crane Egg. as above. Then turn the assembly upside down 2. Cube Assembly: Crease six finished units as and make another pyramid with the three loose explained in the table on page 2. Each face will be made up of 3 the center square of one unit and the tabs of two other units. 4 Do Steps 1 and 2 to form one face. Do Steps 3 and 4 to form one corner or vertex. Continue 1 2 interlocking in this manner to arrive at the finished cube. Sonobe Variations 3 3. Large Cube Assembly: Crease 12 finished units as explained on page 2. 5 6 3 The 12-unit large cube is the only assembly that does not involve pyramidizing.
    [Show full text]