DOCSLIB.ORG

Bayesian Hypothesis Tests Using Nonparametric Statistics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bayesian Hypothesis Tests Using Nonparametric Statistics Statistica Sinica 18(2008), 1185-1200 BAYESIAN HYPOTHESIS TESTS USING NONPARAMETRIC STATISTICS Ying Yuan and Valen E. Johnson University of Texas and M.D. Anderson Cancer Center Abstract: Traditionally, the application of Bayesian testing procedures to classi- cal nonparametric settings has been restricted by difficulties associated with prior specification, prohibitively expensive computation, and the absence of sampling densities for data. To overcome these difficulties, we model the sampling distri- butions of nonparametric test statistics—rather than the sampling distributions of original data—to obtain the Bayes factors required for Bayesian hypothesis tests. We apply this methodology to construct Bayes factors from a wide class of non- parametric test statistics having limiting normal distributions and illustrate these methods with data. Finally, we consider the extension of our methodology to non- parametric test statistics having limiting χ2 distributions. Key words and phrases: Bayes factor, Kruskal-Wallis test, Logrank test, Mann- Whitney-Wilcoxon test, nonparametric hypothesis test, Wilcoxon signed rank test. 1. Introduction In parametric settings, the use of Bayesian methodology for conducting hy- pothesis tests has been limited by two factors. First, the calculation of Bayes factors often involves the evaluation of high-dimensional integrals. This can be a prohibitively expensive undertaking for non-statisticians, both from a numerical and conceptual perspective. Second, Bayes factors require the specification of informative prior densities on parameters appearing in the parametric statistical models that comprise each hypothesis. And unlike Bayesian estimation proce- dures, tests based on Bayes factors retain their sensitivity to prior assumptions even when sample sizes become large. Prior specification is therefore an impor- tant task and one which can be difficult in models containing many parameters. In nonparametric hypothesis testing, a third difficulty arises. Namely, sam- pling distributions for data are not specified. Without sampling distributions for data, Bayesian hypothesis tests cannot be defined. The goal of this article is to overcome these obstacles to Bayesian testing by extending methodology proposed in Johnson (2005) to the classical non- parametric setting. We accomplish this by using results from the asymptotic 1186 YINGYUANANDVALENE.JOHNSON theory of U-statistics and linear rank statistics (e.g., Serfling (1980)) to define al- ternative distributions for test statistics that take the form of Pitman translation alternatives (e.g., Randles and Wolfe (1979)). In so doing, we obtain sampling distributions for non-parametric statistics under alternative models that contain only two unknown parameters: a scale parameter and an asymptotic test-efficacy parameter. Because the distribution of the test statistics under the null hypothesis is known, by specifying a sampling distribution for nonparametric test statistics under a class of alternative models we are able to eliminate two of the obstacles to Bayesian hypothesis testing. That is, by modeling the distribution of test statistics directly we obtain the sampling distributions required for the definition of Bayes factors. We also obtain closed-form expressions for the resulting Bayes factors, which means that numerical evaluation of their values is unnecessary. The third obstacle to the use of Bayes factors—the specification of subjective prior densities—is also considerably simplified. Within our framework, alterna- tive models contain only two scalar parameters. One, the test-efficacy parameter, is determined by the choice of the test statistic. In principle this leaves only a scale parameter for which a prior density must be specified. Methods for handling this parameter are discussed below. To begin, it is worthwhile to review the definition of Bayes factors for the case of nested models. Suppose then that data x arise from a sampling density p(X θ, φ) with unknown parameter vectors θ and φ, and suppose we wish to test | the null hypothesis H : θ = θ0 against the alternative hypothesis H : θ = θ0 0 1 6 where θ0 is assumed known. If p0(x) and p1(x) represent the marginal densities of x under H0 and H1, then the Bayes factor between H0 and H1 can be expressed p (x) p(x θ0, φ)p(φ)dφ B = 0 = | , 01 p (x) p(x θ, φ)p(θ, φ)dθ dφ 1 R | where p(φ) and p(θ, φ) are the priorR densities on unknown parameters under H0 and H1, respectively. Furthermore, if p(H0) and p(H1) denote the prior probabilities assigned to H0 and H1, then the posterior odds of H0 versus H1 is obtained from B01 according to p(H x) p(H ) 0| = 0 B . p(H x) p(H ) 01 1| 1 Thus, Bayes factors represent the weight of evidence contained in data in support of each hypothesis. When deciding between two simple hypotheses, the Bayes factor is simply the likelihood ratio; in more complicated settings it can be re- garded as an integrated likelihood ratio. Further discussion of Bayes factors can be found in, for example, Kass and Raftery (1995). BAYESIAN HYPOTHESIS TESTS USING NONPARAMETRIC STATISTICS 1187 Our motivation for defining Bayes factors based on nonparametric test statis- tics is to avoid the many pitfalls inherent to the use of p values in formal test procedures. For a discussion of these issues in the classical setting, interested readers may consult (among many other articles) Berger and Delampady (1987), Berger and Sellke (1987), and Goodman (1999a,b). Similar issues arise in the use of Bayesian p values for testing model adequacy as described in, for example, Gelman, Meng and Stern (1996) who base their definition of Bayesian p values on posterior-predictive distributions. However, because posterior predictive p values also represent tail-area probabilities, they too are subject to many of the pitfalls inherent to classical p values. As we demonstrate in the sequel, our methodology allows us to transform nonparametric test statistics to an appropriate—and interpretable—probability scale, rather than to what is essentially an uncalibrated and comparatively un- interpretable p-value scale. Our approach is based on the observation that, although the sampling den- sity p(x θ) of the data X may not be specified in nonparametric settings, the | distribution of the test statistic T (X) is often known under both null and alter- native hypotheses, at least asymptotically. To make this notion more precise, we assume for the remainder of this article that the sampling density of the test statistic T (X) can be expressed as p(T (x) θ), where the parameter θ may be | either a scalar or vector-valued parameter. Under the null hypothesis H0, we assume that θ = θ0 for a known value θ0. Under the alternative hypothesis H1, we assume that the sampling distribution of T is obtained by averaging over a prior density p(θ) defined on the domain of θ. When these assumptions hold, the Bayes factor based on t = T (X) can be defined as p(t θ ) BF (t)= | 0 . 01 p(t θ)p(θ)dθ | For suitable choices of p(θ), we find thatR Bayes factors based on nonparametric test statistics can often be expressed in simple form. From such expressions, it is possible to obtain an upper bound on the weight of evidence against the null hypothesis. Such bounds are often useful and may serve to illustrate the maximum extent to which data provide evidence against the null hypothesis. Their use also eliminates much of the subjectivity associated with the definition of Bayes factors. 2. Theory Many nonparametric test statistics have limiting distributions that are either normal or χ2. While our methods can sometimes be applied in finite sample 1188 YINGYUANANDVALENE.JOHNSON settings, it is generally more straightforward to specify alternative distributions in the large sample setting. For this reason, we restrict attention to this case and begin with nonparametric statistics that have limiting normal distributions. The asymptotic normality of a variety of nonparametric test statistics has been established by the theory of U-statistics and linear rank statistics (e.g., Serfling (1980)). These results are widely used in practice to approximate the exact sampling distributions of nonparametric test statistics, which often do not have closed forms and have to be computed numerically. The class of nonparametric test statistics with limiting normal distribu- tions includes many commonly used nonparametric statistics. Among these are the sign test and Wilcoxon signed rank test for one-sample location problems, the Mann-Whitney-Wilcoxon test for two-sample location problems, the Ansari- Bradley test and Mood test for scale problems, Kendall’s tau and Spearman test for testing independence, the Theil test for slope parameters in regression problems, the Mantel test (or logrank test), and the Hollander-Proschan test of exponentiality in survival analysis. In order to describe how statistics from these tests can be used to define Bayes factors, let Tk, k = 1, 2 . ., denote a sequence of nonparametric test statistics based on nk observations, and suppose that nk as k . Consider the → ∞ → ∞ test of the null hypothesis H0 : θ = θ0 versus the local alternative H1(nk) : θk = θ0 +∆/√nk, where ∆ is a bounded constant. This form of the alternative hypothesis is often called the Pitman translation alternative (e.g., Randles and Wolfe (1979)). Our attention focuses on the asymptotic distribution of the standardized value of Tk, ∗ Tk µk(θ0) Tk = − , σk(θ0) where µk and σk are the mean and standard deviation of Tk, respectively. Under ∗ H0, we assume that Tk has a limiting standard normal distribution. Under ∗ H1(nk), the asymptotic distribution of Tk is given in the following lemma. The proof follows Noether (1955) and appears in the Appendix. Lemma 1. Assume H1(nk) and L (A1) [Tk µk(θk)]/σk(θk) N(0, 1); − p −→ (A2) σk(θk)/σk(θ ) 1; 0 −→ (A3) µk(θ) is differentiable at θ0; BAYESIAN HYPOTHESIS TESTS USING NONPARAMETRIC STATISTICS 1189 ′ p (A4) µk(θ0)/√nkσk(θ0) C where C is a constant.
Load more

Recommended publications
  • Nonparametric Statistics for Social and Behavioral Sciences
    Statistics Incorporating a hands-on approach, Nonparametric Statistics for Social SOCIAL AND BEHAVIORAL SCIENCES and Behavioral Sciences presents the concepts, principles, and methods NONPARAMETRIC STATISTICS FOR used in performing many nonparametric procedures. It also demonstrates practical applications of the most common nonparametric procedures using IBM’s SPSS software. Emphasizing sound research designs, appropriate statistical analyses, and NONPARAMETRIC accurate interpretations of results, the text: • Explains a conceptual framework for each statistical procedure STATISTICS FOR • Presents examples of relevant research problems, associated research questions, and hypotheses that precede each procedure • Details SPSS paths for conducting various analyses SOCIAL AND • Discusses the interpretations of statistical results and conclusions of the research BEHAVIORAL With minimal coverage of formulas, the book takes a nonmathematical ap- proach to nonparametric data analysis procedures and shows you how they are used in research contexts. Each chapter includes examples, exercises, SCIENCES and SPSS screen shots illustrating steps of the statistical procedures and re- sulting output. About the Author Dr. M. Kraska-Miller is a Mildred Cheshire Fraley Distinguished Professor of Research and Statistics in the Department of Educational Foundations, Leadership, and Technology at Auburn University, where she is also the Interim Director of Research for the Center for Disability Research and Service. Dr. Kraska-Miller is the author of four books on teaching and communications. She has published numerous articles in national and international refereed journals. Her research interests include statistical modeling and applications KRASKA-MILLER of statistics to theoretical concepts, such as motivation; satisfaction in jobs, services, income, and other areas; and needs assessments particularly applicable to special populations.
    [Show full text]
  • Logrank Tests (Freedman)
    PASS Sample Size Software NCSS.com Chapter 702 Logrank Tests (Freedman) Introduction This module allows the sample size and power of the logrank test to be analyzed under the assumption of proportional hazards. Time periods are not stated. Rather, it is assumed that enough time elapses to allow for a reasonable proportion of responses to occur. If you want to study the impact of accrual and follow-up time, you should use the one of the other logrank modules available in PASS. The formulas used in this module come from Machin et al. (2018). They are also given in Fayers and Machin (2016) where they are applied to sizing quality of life studies. They were originally published in Freedman (1982) and are often referred to by that name. A clinical trial is often employed to test the equality of survival distributions for two treatment groups. For example, a researcher might wish to determine if Beta-Blocker A enhances the survival of newly diagnosed myocardial infarction patients over that of the standard Beta-Blocker B. The question being considered is whether the pattern of survival is different. The two-sample t-test is not appropriate for two reasons. First, the data consist of the length of survival (time to failure), which is often highly skewed, so the usual normality assumption cannot be validated. Second, since the purpose of the treatment is to increase survival time, it is likely (and desirable) that some of the individuals in the study will survive longer than the planned duration of the study. The survival times of these individuals are then unobservable and are said to be censored.
    [Show full text]
  • Randomization-Based Test for Censored Outcomes: a New Look at the Logrank Test
    Randomization-based Test for Censored Outcomes: A New Look at the Logrank Test Xinran Li and Dylan S. Small ∗ Abstract Two-sample tests have been one of the most classical topics in statistics with wide appli- cation even in cutting edge applications. There are at least two modes of inference used to justify the two-sample tests. One is usual superpopulation inference assuming the units are independent and identically distributed (i.i.d.) samples from some superpopulation; the other is finite population inference that relies on the random assignments of units into different groups. When randomization is actually implemented, the latter has the advantage of avoiding distribu- tional assumptions on the outcomes. In this paper, we will focus on finite population inference for censored outcomes, which has been less explored in the literature. Moreover, we allow the censoring time to depend on treatment assignment, under which exact permutation inference is unachievable. We find that, surprisingly, the usual logrank test can also be justified by ran- domization. Specifically, under a Bernoulli randomized experiment with non-informative i.i.d. censoring within each treatment arm, the logrank test is asymptotically valid for testing Fisher's null hypothesis of no treatment effect on any unit. Moreover, the asymptotic validity of the lo- grank test does not require any distributional assumption on the potential event times. We further extend the theory to the stratified logrank test, which is useful for randomized blocked designs and when censoring mechanisms vary across strata. In sum, the developed theory for the logrank test from finite population inference supplements its classical theory from usual superpopulation inference, and helps provide a broader justification for the logrank test.
    [Show full text]
  • Nonparametric Estimation by Convex Programming
    The Annals of Statistics 2009, Vol. 37, No. 5A, 2278–2300 DOI: 10.1214/08-AOS654 c Institute of Mathematical Statistics, 2009 NONPARAMETRIC ESTIMATION BY CONVEX PROGRAMMING By Anatoli B. Juditsky and Arkadi S. Nemirovski1 Universit´eGrenoble I and Georgia Institute of Technology The problem we concentrate on is as follows: given (1) a convex compact set X in Rn, an affine mapping x 7→ A(x), a parametric family {pµ(·)} of probability densities and (2) N i.i.d. observations of the random variable ω, distributed with the density pA(x)(·) for some (unknown) x ∈ X, estimate the value gT x of a given linear form at x. For several families {pµ(·)} with no additional assumptions on X and A, we develop computationally efficient estimation routines which are minimax optimal, within an absolute constant factor. We then apply these routines to recovering x itself in the Euclidean norm. 1. Introduction. The problem we are interested in is essentially as fol- lows: suppose that we are given a convex compact set X in Rn, an affine mapping x A(x) and a parametric family pµ( ) of probability densities. Suppose that7→N i.i.d. observations of the random{ variable· } ω, distributed with the density p ( ) for some (unknown) x X, are available. Our objective A(x) · ∈ is to estimate the value gT x of a given linear form at x. In nonparametric statistics, there exists an immense literature on various versions of this problem (see, e.g., [10, 11, 12, 13, 15, 17, 18, 21, 22, 23, 24, 25, 26, 27, 28] and the references therein).
    [Show full text]
  • Survival Analysis Using a 5‐Step Stratified Testing and Amalgamation
    Received: 13 March 2020 Revised: 25 June 2020 Accepted: 24 August 2020 DOI: 10.1002/sim.8750 RESEARCH ARTICLE Survival analysis using a 5-step stratified testing and amalgamation routine (5-STAR) in randomized clinical trials Devan V. Mehrotra Rachel Marceau West Biostatistics and Research Decision Sciences, Merck & Co., Inc., North Wales, Randomized clinical trials are often designed to assess whether a test treatment Pennsylvania, USA prolongs survival relative to a control treatment. Increased patient heterogene- ity, while desirable for generalizability of results, can weaken the ability of Correspondence Devan V. Mehrotra, Biostatistics and common statistical approaches to detect treatment differences, potentially ham- Research Decision Sciences, Merck & Co., pering the regulatory approval of safe and efficacious therapies. A novel solution Inc.,NorthWales,PA,USA. Email: [email protected] to this problem is proposed. A list of baseline covariates that have the poten- tial to be prognostic for survival under either treatment is pre-specified in the analysis plan. At the analysis stage, using all observed survival times but blinded to patient-level treatment assignment, “noise” covariates are removed with elastic net Cox regression. The shortened covariate list is used by a condi- tional inference tree algorithm to segment the heterogeneous trial population into subpopulations of prognostically homogeneous patients (risk strata). After patient-level treatment unblinding, a treatment comparison is done within each formed risk stratum and stratum-level results are combined for overall statis- tical inference. The impressive power-boosting performance of our proposed 5-step stratified testing and amalgamation routine (5-STAR), relative to that of the logrank test and other common approaches that do not leverage inherently structured patient heterogeneity, is illustrated using a hypothetical and two real datasets along with simulation results.
    [Show full text]
  • Repeated-Measures ANOVA & Friedman Test Using STATCAL
    Repeated-Measures ANOVA & Friedman Test Using STATCAL (R) & SPSS Prana Ugiana Gio Download STATCAL in www.statcal.com i CONTENT 1.1 Example of Case 1.2 Explanation of Some Book About Repeated-Measures ANOVA 1.3 Repeated-Measures ANOVA & Friedman Test 1.4 Normality Assumption and Assumption of Equality of Variances (Sphericity) 1.5 Descriptive Statistics Based On SPSS dan STATCAL (R) 1.6 Normality Assumption Test Using Kolmogorov-Smirnov Test Based on SPSS & STATCAL (R) 1.7 Assumption Test of Equality of Variances Using Mauchly Test Based on SPSS & STATCAL (R) 1.8 Repeated-Measures ANOVA Based on SPSS & STATCAL (R) 1.9 Multiple Comparison Test Using Boferroni Test Based on SPSS & STATCAL (R) 1.10 Friedman Test Based on SPSS & STATCAL (R) 1.11 Multiple Comparison Test Using Wilcoxon Test Based on SPSS & STATCAL (R) ii 1.1 Example of Case For example given data of weight of 11 persons before and after consuming medicine of diet for one week, two weeks, three weeks and four week (Table 1.1.1). Tabel 1.1.1 Data of Weight of 11 Persons Weight Name Before One Week Two Weeks Three Weeks Four Weeks A 89.43 85.54 80.45 78.65 75.45 B 85.33 82.34 79.43 76.55 71.35 C 90.86 87.54 85.45 80.54 76.53 D 91.53 87.43 83.43 80.44 77.64 E 90.43 84.45 81.34 78.64 75.43 F 90.52 86.54 85.47 81.44 78.64 G 87.44 83.34 80.54 78.43 77.43 H 89.53 86.45 84.54 81.35 78.43 I 91.34 88.78 85.47 82.43 78.76 J 88.64 84.36 80.66 78.65 77.43 K 89.51 85.68 82.68 79.71 76.5 Average 89.51 85.68 82.68 79.71 76.69 Based on Table 1.1.1: The person whose name is A has initial weight 89,43, after consuming medicine of diet for one week 85,54, two weeks 80,45, three weeks 78,65 and four weeks 75,45.
    [Show full text]
  • Applied Biostatistics Applied Biostatistics for the Pulmonologist
    APPLIED BIOSTATISTICS FOR THE PULMONOLOGIST DR. VISHWANATH GELLA • Statistics is a way of thinking about the world and decision making-By Sir RA Fisher Why do we need statistics? • A man with one watch always knows what time it is • A man with two watches always searches to identify the correct one • A man with ten watches is always reminded of the difficu lty in measuri ng ti me Objectives • Overview of Biostatistical Terms and Concepts • Application of Statistical Tests Types of statistics • Descriptive Statistics • identify patterns • leads to hypothesis generation • Inferential Statistics • distinguish true differences from random variation • allows hypothesis testing Study design • Analytical studies Case control study(Effect to cause) Cohort study(Cause to effect) • Experimental studies Randomized controlled trials Non-randomized trials Sample size estimation • ‘Too small’ or ‘Too large’ • Sample size depends upon four critical quantities: Type I & II error stat es ( al ph a & b et a errors) , th e vari abilit y of th e d at a (S.D)2 and the effect size(d) • For two group parallel RCT with a continuous outcome - sample size(n) per group = 16(S.D)2/d2 for fixed alpha and beta values • Anti hypertensive trial- effect size= 5 mmHg, S.D of the data- 10 mm Hggp. n= 16 X 100/25= 64 patients per group in the study • Statistical packages - PASS in NCSS, n query or sample power TYPES OF DATA • Quant itat ive (“how muc h?”) or categor ica l variable(“what type?”) • QiiiblQuantitative variables 9 continuous- Blood pressure, height, weight or age 9 Discrete- No.
    [Show full text]
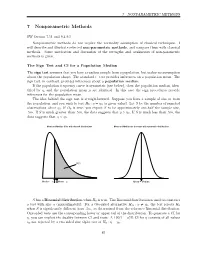
  • 7 Nonparametric Methods
    7 NONPARAMETRIC METHODS 7 Nonparametric Methods SW Section 7.11 and 9.4-9.5 Nonparametric methods do not require the normality assumption of classical techniques. I will describe and illustrate selected non-parametric methods, and compare them with classical methods. Some motivation and discussion of the strengths and weaknesses of non-parametric methods is given. The Sign Test and CI for a Population Median The sign test assumes that you have a random sample from a population, but makes no assumption about the population shape. The standard t−test provides inferences on a population mean. The sign test, in contrast, provides inferences about a population median. If the population frequency curve is symmetric (see below), then the population median, iden- tified by η, and the population mean µ are identical. In this case the sign procedures provide inferences for the population mean. The idea behind the sign test is straightforward. Suppose you have a sample of size m from the population, and you wish to test H0 : η = η0 (a given value). Let S be the number of sampled observations above η0. If H0 is true, you expect S to be approximately one-half the sample size, .5m. If S is much greater than .5m, the data suggests that η > η0. If S is much less than .5m, the data suggests that η < η0. Mean and Median differ with skewed distributions Mean and Median are the same with symmetric distributions 50% Median = η Mean = µ Mean = Median S has a Binomial distribution when H0 is true. The Binomial distribution is used to construct a test with size α (approximately).
    [Show full text]
  • 9 Blocked Designs
    9 Blocked Designs 9.1 Friedman's Test 9.1.1 Application 1: Randomized Complete Block Designs • Assume there are k treatments of interest in an experiment. In Section 8, we considered the k-sample Extension of the Median Test and the Kruskal-Wallis Test to test for any differences in the k treatment medians. • Suppose the experimenter is still concerned with studying the effects of a single factor on a response of interest, but variability from another factor that is not of interest is expected. { Suppose a researcher wants to study the effect of 4 fertilizers on the yield of cotton. The researcher also knows that the soil conditions at the 8 areas for performing an experiment are highly variable. Thus, the researcher wants to design an experiment to detect any differences among the 4 fertilizers on the cotton yield in the presence a \nuisance variable" not of interest (the 8 areas). • Because experimental units can vary greatly with respect to physical characteristics that can also influence the response, the responses from experimental units that receive the same treatment can also vary greatly. • If it is not controlled or accounted for in the data analysis, it can can greatly inflate the experimental variability making it difficult to detect real differences among the k treatments of interest (large Type II error). • If this source of variability can be separated from the treatment effects and the random experimental error, then the sensitivity of the experiment to detect real differences between treatments in increased (i.e., lower the Type II error). • Therefore, the goal is to choose an experimental design in which it is possible to control the effects of a variable not of interest by bringing experimental units that are similar into a group called a \block".
    [Show full text]
  • DETECTION MONITORING TESTS Unified Guidance
    PART III. DETECTION MONITORING TESTS Unified Guidance PART III. DETECTION MONITORING TESTS This third part of the Unified Guidance presents core procedures recommended for formal detection monitoring at RCRA-regulated facilities. Chapter 16 describes two-sample tests appropriate for some small facilities, facilities in interim status, or for periodic updating of background data. These tests include two varieties of the t-test and two non-parametric versions-- the Wilcoxon rank-sum and Tarone-Ware procedures. Chapter 17 discusses one-way analysis of variance [ANOVA], tolerance limits, and the application of trend tests during detection monitoring. Chapter 18 is a primer on several kinds of prediction limits, which are combined with retesting strategies in Chapter 19 to address the statistical necessity of performing multiple comparisons during RCRA statistical evaluations. Retesting is also discussed in Chapter 20, which presents control charts as an alternative to prediction limits. As discussed in Section 7.5, any of these detection-level tests may also be applied to compliance/assessment and corrective action monitoring, where a background groundwater protection standard [GWPS] is defined as a critical limit using two- or multiple-sample comparison tests. Caveats and limitations discussed for detection monitoring tests are also relevant to this situation. To maintain continuity of presentation, this additional application is presumed but not repeated in the following specific test and procedure discussions. Although other users and programs may find these statistical tests of benefit due to their wider applicability to other environmental media and types of data, the methods described in Parts III and IV are primarily tailored to the RCRA setting and designed to address formal RCRA monitoring requirements.
    [Show full text]
  • 4. Comparison of Two (K) Samples K=2 Problem: Compare the Survival Distributions Between Two Groups
    4. Comparison of Two (K) Samples K=2 Problem: compare the survival distributions between two groups. Ex: comparing treatments on patients with a particular disease. 푍: Treatment indicator, i.e. 푍 = 1 for treatment 1 (new treatment); 푍 = 0 for treatment 0 (standard treatment or placebo) Null Hypothesis: H0: no treatment (group) difference H0: 푆0 푡 = 푆1 푡 , for 푡 ≥ 0 H0: 휆0 푡 = 휆1 푡 , for 푡 ≥ 0 Alternative Hypothesis: Ha: the survival time for one treatment is stochastically larger or smaller than the survival time for the other treatment. Ha: 푆1 푡 ≥ 푆0 푡 , for 푡 ≥ 0 with strict inequality for some 푡 (one-sided) Ha: either 푆1 푡 ≥ 푆0 푡 , or 푆0 푡 ≥ 푆1 푡 , for 푡 ≥ 0 with strict inequality for some 푡 Solution: In biomedical applications, it has become common practice to use nonparametric tests; that is, using test statistics whose distribution under the null hypothesis does not depend on specific parametric assumptions on the shape of the probability distribution. With censored survival data, the class of weighted logrank tests are mostly used, with the logrank test being the most commonly used. Notations A sample of triplets 푋푖, Δ푖, 푍푖 , 푖 = 1, 2, … , 푛, where 1 푛푒푤 푡푟푒푎푡푚푒푛푡 푋푖 = min(푇푖, 퐶푖) Δ푖 = 퐼 푇푖 ≤ 퐶푖 푍 = ቊ 푖 0 푠푡푎푛푑푎푟푑 푇푟푒푎푡푚푒푛푡 푇푖 = latent failure time; 퐶푖 = latent censoring time Also, define, 푛 푛1 = number of individuals in group 1 푛푗 = ෍ 퐼(푍푗 = 푗) , 푗 = 0, 1 푛0 = number of individuals in group 0 푖=1 푛 = 푛0 + 푛1 푛 푌1(푥) = number of individuals at risk at time 푥 from trt 1 = σ푖=1 퐼(푋푖 ≥ 푥, 푍푖 = 1) 푛 푌0(푥) = number of individuals at risk at time 푥 from trt 0 = σ푖=1 퐼(푋푖 ≥ 푥, 푍푖 = 0) 푌(푥) = 푌0(푥) + 푌1(푥) 푛 푑푁1(푥) = # of deaths observed at time 푥 from trt 1 = σ푖=1 퐼(푋푖 = 푥, Δ푖 = 1, 푍푖 = 1) 푛 푑푁0(푥) = # of deaths observed at time 푥 from trt 0 = σ푖=1 퐼(푋푖 = 푥, Δ푖 = 1, 푍푖 = 0) 푛 푑푁 푥 = 푑푁0 푥 + 푑푁1 푥 = σ푖=1 퐼(푋푖 = 푥, Δ푖 = 1) Note: 푑푁 푥 actually correspond to the observed number of deaths in time window 푥, 푥 + Δ푥 for some partition of the time axis into intervals of length Δ푥.
    [Show full text]
  • Kaplan-Meier Curves (Logrank Tests)
    NCSS Statistical Software NCSS.com Chapter 555 Kaplan-Meier Curves (Logrank Tests) Introduction This procedure computes the nonparametric Kaplan-Meier and Nelson-Aalen estimates of survival and associated hazard rates. It can fit complete, right censored, left censored, interval censored (readout), and grouped data values. It outputs various statistics and graphs that are useful in reliability and survival analysis. It also performs several logrank tests and provides both the parametric and randomization test significance levels. This procedure also computes restricted mean survival time (RMST) and restricted mean time lost (RMTL) statistics and associated between-group comparisons. Overview of Survival Analysis We will give a brief introduction to the subject in this section. For a complete account of survival analysis, we suggest the book by Klein and Moeschberger (2003). Survival analysis is the study of the distribution of life times. That is, it is the study of the elapsed time between an initiating event (birth, start of treatment, diagnosis, or start of operation) and a terminal event (death, relapse, cure, or machine failure). The data values are a mixture of complete (terminal event occurred) and censored (terminal event has not occurred) observations. From the data values, the survival analyst makes statements about the survival distribution of the failure times. This distribution allows questions about such quantities as survivability, expected life time, and mean time to failure to be answered. Let T be the elapsed time until the occurrence of a specified event. The event may be death, occurrence of a disease, disappearance of a disease, appearance of a tumor, etc. The probability distribution of T may be specified using one of the following basic functions.
    [Show full text]