DOCSLIB.ORG

Nonparametric Statistics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Nonparametric Statistics 14 Nonparametric Statistics • These methods required that the data be normally CONTENTS distributed or that the sampling distributions of the 14.1 Introduction: Distribution-Free Tests relevant statistics be normally distributed. 14.2 Single-Population Inferences Where We're Going 14.3 Comparing Two Populations: • Develop the need for inferential techniques that Independent Samples require fewer or less stringent assumptions than the 14.4 Comparing Two Populations: Paired methods of Chapters 7 – 10 and 11 (14.1) Difference Experiment • Introduce nonparametric tests that are based on ranks 14.5 Comparing Three or More Populations: (i.e., on an ordering of the sample measurements Completely Randomized Design according to their relative magnitudes) (14.2–14.7) • Present a nonparametric test about the central 14.6 Comparing Three or More Populations: tendency of a single population (14.2) Randomized Block Design • Present a nonparametric test for comparing two 14.7 Rank Correlation populations with independent samples (14.3) • Present a nonparametric test for comparing two Where We've Been populations with paired samples (14.4) • Presented methods for making inferences about • Present a nonparametric test for comparing three or means ( Chapters 7 – 10 ) and for making inferences more populations using a designed experiment about the correlation between two quantitative (14.5–14.6) variables ( Chapter 11 ) • Present a nonparametric test for rank correlation (14.7) 14-1 Copyright (c) 2013 Pearson Education, Inc M14_MCCL6947_12_AIE_C14.indd 14-1 10/1/11 9:59 AM Statistics IN Action How Vulnerable Are New Hampshire Wells to Groundwater Contamination? Methyl tert- butyl ether (commonly known as MTBE) is a the measuring device, the MTBE val- volatile, flammable, colorless liquid manufactured by the chemi- ues for these wells are recorded as .2 cal reaction of methanol and isobutylene. MTBE was first rather than 0.) The other produced in the United States as a lead fuel additive (octane variables in the data set are booster) in 1979 and then as an oxygenate in reformulated described in Table SIA14.1 . fuel in the 1990s. Unfortunately, MTBE was introduced into How contaminated are water-supply aquifers by leaking underground storage tanks these New Hampshire wells? at gasoline stations, thus contaminating the drinking water. Is the level of MTBE con- Consequently, by late 2006 most (but not all) American gasoline tamination different for the two classes of wells? For the two retailers had ceased using MTBE as an oxygenate, and accord- types of aquifers? What environmental factors are related to the ingly, U.S. production has declined. Despite the reduction in pro- MTBE level of a groundwater well? These are just a few of the duction, there is no federal standard for MTBE in public water research questions addressed in the study. supplies; therefore, the chemical remains a dangerous pollutant, The researchers applied several nonparametric meth- especially in states like New Hampshire that mandate the use of ods to the data in order to answer the research questions. We reformulated gasoline. demonstrate the use of this methodology in four Statistics in A study published in Environmental Science & Technol- Action Revisited examples. ogy (Jan. 2005) investigated the risk of exposure to MTBE through drinking water in New Hampshire. In particular, the Statistics IN Action Revisited study reported on the factors related to MTBE contamina- • Testing the Median MTBE Level of Groundwater Wells tion in public and private New Hampshire wells. Data were (p. 14-7) collected on a sample of 223 wells. These data are saved in the • Comparing the MTBE Levels of Different Types of MTBE file (part of which you analyzed in Exercise 2.19). One Groundwater Wells (p. 14-14) of the variables measured was MTBE level (micrograms per liter) in the well water. An MTBE value exceeding .2 micro- • Comparing the MTBE Levels of Different Types of gram per liter on the measuring instrument is a detectable level Groundwater Wells (continued) (p. 14-30) of MTBE. Of the 223 wells, 70 had detectable levels of MTBE. • Testing the Correlation of MTBE Level with Other Envi- (Although the other wells are below the detection limit of ronmental Factors (p. 14-44) Table SIA14.1 Variables Measured in the MTBE Contamination Study Variable Name Type Description Units of Measurement, or Levels CLASS QL Class of well Public or Private AQUIFER QL Type of aquifer Bedrock or Unconsolidated DETECTION QL MTBE detection status Below limit or Detect MTBE QN MTBE level micrograms per liter PH QN pH level standard pH unit DISSOXY QN Dissolved oxygen milligrams per liter DEPTH QN Well depth meters DISTANCE QN Distance to underground storage tank meters INDUSTRY QN Industries in proximity Percent of industrial land within 500 meters of well Data Set: MTBE 14.1 Introduction: Distribution-Free Tests The confidence interval and testing procedures developed in Chapters 7 – 10 all involve making inferences about population parameters. Consequently, they are often referred to as parametric statistical tests. Many of these parametric methods (e.g., the small-sample t -test of Chapter 8 or the ANOVA F-test of Chapter 10 ) rely on the assumption that the data are sampled from a normally distributed population. When the data are normal, these tests are most powerful . That is, the use of such parametric tests maximizes power— 14-2 the probability of the researcher correctly rejecting the null hypothesis. Copyright (c) 2013 Pearson Education, Inc M14_MCCL6947_12_AIE_C14.indd 14-2 10/1/11 9:59 AM SECTION 14.1 Introduction: Distribution-Free Tests 14-3 Consider a population of data that is decidedly nonnormal. For example, the dis- tribution might be flat, peaked, or strongly skewed to the right or left. (See Figure 14.1 .) Applying the small-sample t -test to such a data set may lead to serious consequences. Since the normality assumption is clearly violated, the results of the t -test are unreli- able. Specifically, (1) the probability of a Type I error (i.e., rejecting H0 when it is true) may be larger than the value of a selected, and (2) the power of the test, 1 - b, is not maximized. Figure 14.1 Some nonnormal distributions for which the t -statistic is invalid a. Flat distribution b. Peaked distribution c. Skewed distribution A number of nonparametric techniques are available for analyzing data that do not follow a normal distribution. Nonparametric tests do not depend on the distribution of the sampled population; thus, they are called distribution-free tests . Also, nonpara- metric methods focus on the location of the probability distribution of the population, rather than on specific parameters of the population, such as the mean (hence the name “nonparametric”). Distribution-free tests are statistical tests that do not rely on any underlying assump- tions about the probability distribution of the sampled population. The branch of inferential statistics devoted to distribution-free tests is called non- parametrics . Nonparametric tests are also appropriate when the data are nonnumerical in nature, but can be ranked. * For example, when taste-testing foods or in other types of consumer product evaluations, we can say that we like product A better than product B, and B better than C, but we cannot obtain exact quantitative values for the respec- tive measurements. Nonparametric tests based on the ranks of measurements are called rank tests . Nonparametric statistics (or tests) based on the ranks of measurements are called rank statistics (or rank tests ). Ethics IN Statistics Consider a sampling problem where the assumptions required In this chapter, we present several useful nonparametric methods. Keep in mind for the valid application of a that these nonparametric tests are more powerful than their corresponding parametric parametric procedure (e.g., a t -test counterparts in those situations where either the data are nonnormal or the data are for a population mean) are clearly ranked. violated. Also, suppose the results In Section 14.2, we develop a test for making inferences about the central tendency of the parametric test lead you to a of a single population. In Sections 14.3 and 14.5, we present rank statistics for comparing different inference about the target two or more probability distributions using independent samples. In Sections 14.4 and population than the corresponding 14.6, the matched-pairs and randomized block designs are used to make nonparametric nonparametric method. Intentional comparisons of populations. Finally, in Section 14.7, we present a nonparametric mea- reporting of only the parametric sure of correlation between two variables. test results is considered unethical statistical practice . * Qualitative data that can be ranked in order of magnitude are called ordinal data. Copyright (c) 2013 Pearson Education, Inc M14_MCCL6947_12_AIE_C14.indd 14-3 10/1/11 9:59 AM 14-4 CHAPTER 14 Nonparametric Statistics 14.2 Single-Population Inferences In Chapter 8 , we utilized the z - and t -statistics for testing hypotheses about a population mean. The z -statistic is appropriate for large random samples selected from “general” populations—that is, samples with few limitations on the probability distribution of the underlying population. The t -statistic was developed for small-sample tests in which the sample is selected at random from a normal distribution. The question is, How can we conduct a test of hypothesis when we have a small sample from a nonnormal distribution? The sign test is a relatively simple nonparametric procedure for testing hypotheses about the central tendency of a nonnormal probability distribution. Note that we used the phrase central tendency rather than population mean . This is because the sign test, like many nonparametric procedures, provides inferences about the population median rather than the population mean m. Denoting the population median by the Greek letter h, we know ( Chapter 2 ) that h is the 50th per- centile of the distribution ( Figure 14.2 ) and, as such, Area = .5 is less affected by the skewness of the distribution and the presence of outliers (extreme observations).
Load more

Recommended publications
  • Appendix a Basic Statistical Concepts for Sensory Evaluation
    Appendix A Basic Statistical Concepts for Sensory Evaluation Contents This chapter provides a quick introduction to statistics used for sensory evaluation data including measures of A.1 Introduction ................ 473 central tendency and dispersion. The logic of statisti- A.2 Basic Statistical Concepts .......... 474 cal hypothesis testing is introduced. Simple tests on A.2.1 Data Description ........... 475 pairs of means (the t-tests) are described with worked A.2.2 Population Statistics ......... 476 examples. The meaning of a p-value is reviewed. A.3 Hypothesis Testing and Statistical Inference .................. 478 A.3.1 The Confidence Interval ........ 478 A.3.2 Hypothesis Testing .......... 478 A.3.3 A Worked Example .......... 479 A.1 Introduction A.3.4 A Few More Important Concepts .... 480 A.3.5 Decision Errors ............ 482 A.4 Variations of the t-Test ............ 482 The main body of this book has been concerned with A.4.1 The Sensitivity of the Dependent t-Test for using good sensory test methods that can generate Sensory Data ............. 484 quality data in well-designed and well-executed stud- A.5 Summary: Statistical Hypothesis Testing ... 485 A.6 Postscript: What p-Values Signify and What ies. Now we turn to summarize the applications of They Do Not ................ 485 statistics to sensory data analysis. Although statistics A.7 Statistical Glossary ............. 486 are a necessary part of sensory research, the sensory References .................... 487 scientist would do well to keep in mind O’Mahony’s admonishment: statistical analysis, no matter how clever, cannot be used to save a poor experiment. The techniques of statistical analysis, do however, It is important when taking a sample or designing an serve several useful purposes, mainly in the efficient experiment to remember that no matter how powerful summarization of data and in allowing the sensory the statistics used, the inferences made from a sample scientist to make reasonable conclusions from the are only as good as the data in that sample.
    [Show full text]
  • Nonparametric Statistics for Social and Behavioral Sciences
    Statistics Incorporating a hands-on approach, Nonparametric Statistics for Social SOCIAL AND BEHAVIORAL SCIENCES and Behavioral Sciences presents the concepts, principles, and methods NONPARAMETRIC STATISTICS FOR used in performing many nonparametric procedures. It also demonstrates practical applications of the most common nonparametric procedures using IBM’s SPSS software. Emphasizing sound research designs, appropriate statistical analyses, and NONPARAMETRIC accurate interpretations of results, the text: • Explains a conceptual framework for each statistical procedure STATISTICS FOR • Presents examples of relevant research problems, associated research questions, and hypotheses that precede each procedure • Details SPSS paths for conducting various analyses SOCIAL AND • Discusses the interpretations of statistical results and conclusions of the research BEHAVIORAL With minimal coverage of formulas, the book takes a nonmathematical ap- proach to nonparametric data analysis procedures and shows you how they are used in research contexts. Each chapter includes examples, exercises, SCIENCES and SPSS screen shots illustrating steps of the statistical procedures and re- sulting output. About the Author Dr. M. Kraska-Miller is a Mildred Cheshire Fraley Distinguished Professor of Research and Statistics in the Department of Educational Foundations, Leadership, and Technology at Auburn University, where she is also the Interim Director of Research for the Center for Disability Research and Service. Dr. Kraska-Miller is the author of four books on teaching and communications. She has published numerous articles in national and international refereed journals. Her research interests include statistical modeling and applications KRASKA-MILLER of statistics to theoretical concepts, such as motivation; satisfaction in jobs, services, income, and other areas; and needs assessments particularly applicable to special populations.
    [Show full text]
  • Krishnan Correlation CUSB.Pdf
    SELF INSTRUCTIONAL STUDY MATERIAL PROGRAMME: M.A. DEVELOPMENT STUDIES COURSE: STATISTICAL METHODS FOR DEVELOPMENT RESEARCH (MADVS2005C04) UNIT III-PART A CORRELATION PROF.(Dr). KRISHNAN CHALIL 25, APRIL 2020 1 U N I T – 3 :C O R R E L A T I O N After reading this material, the learners are expected to : . Understand the meaning of correlation and regression . Learn the different types of correlation . Understand various measures of correlation., and, . Explain the regression line and equation 3.1. Introduction By now we have a clear idea about the behavior of single variables using different measures of Central tendency and dispersion. Here the data concerned with one variable is called ‗univariate data‘ and this type of analysis is called ‗univariate analysis‘. But, in nature, some variables are related. For example, there exists some relationships between height of father and height of son, price of a commodity and amount demanded, the yield of a plant and manure added, cost of living and wages etc. This is a a case of ‗bivariate data‘ and such analysis is called as ‗bivariate data analysis. Correlation is one type of bivariate statistics. Correlation is the relationship between two variables in which the changes in the values of one variable are followed by changes in the values of the other variable. 3.2. Some Definitions 1. ―When the relationship is of a quantitative nature, the approximate statistical tool for discovering and measuring the relationship and expressing it in a brief formula is known as correlation‖—(Craxton and Cowden) 2. ‗correlation is an analysis of the co-variation between two or more variables‖—(A.M Tuttle) 3.
    [Show full text]
  • ED441031.Pdf
    DOCUMENT RESUME ED 441 031 TM 030 830 AUTHOR Fahoome, Gail; Sawilowsky, Shlomo S. TITLE Review of Twenty Nonparametric Statistics and Their Large Sample Approximations. PUB DATE 2000-04-00 NOTE 42p.; Paper presented at the Annual Meeting of the American Educational Research Association (New Orleans, LA, April 24-28, 2000). PUB TYPE Information Analyses (070)-- Numerical/Quantitative Data (110) Speeches/Meeting Papers (150) EDRS PRICE MF01/PCO2 Plus Postage. DESCRIPTORS Monte Carlo Methods; *Nonparametric Statistics; *Sample Size; *Statistical Distributions ABSTRACT Nonparametric procedures are often more powerful than classical tests for real world data, which are rarely normally distributed. However, there are difficulties in using these tests. Computational formulas are scattered tnrous-hout the literature, and there is a lack of avalialalicy of tables of critical values. This paper brings together the computational formulas for 20 commonly used nonparametric tests that have large-sample approximations for the critical value. Because there is no generally agreed upon lower limit for the sample size, Monte Carlo methods have been used to determine the smallest sample size that can be used with the large-sample approximations. The statistics reviewed include single-population tests, comparisons of two populations, comparisons of several populations, and tests of association. (Contains 4 tables and 59 references.)(Author/SLD) Reproductions supplied by EDRS are the best that can be made from the original document. Review of Twenty Nonparametric Statistics and Their Large Sample Approximations Gail Fahoome Shlomo S. Sawilowsky U.S. DEPARTMENT OF EDUCATION Mice of Educational Research and Improvement PERMISSION TO REPRODUCE AND UCATIONAL RESOURCES INFORMATION DISSEMINATE THIS MATERIAL HAS f BEEN GRANTED BY CENTER (ERIC) This document has been reproduced as received from the person or organization originating it.
    [Show full text]
  • Detecting Trends Using Spearman's Rank Correlation Coefficient
    Environmental Forensics 2001) 2, 359±362 doi:10.1006/enfo.2001.0061, available online at http://www.idealibrary.com on Detecting Trends Using Spearman's Rank Correlation Coecient Thomas D. Gauthier Sciences International Inc, 6150 State Road 70, East Bradenton, FL 34203, U.S.A. Received 23 August 2001, Revised manuscript accepted 1 October 2001) Spearman's rank correlation coecient is a useful tool for exploratory data analysis in environmental forensic investigations. In this application it is used to detect monotonic trends in chemical concentration with time or space. # 2001 AEHS Keywords: Spearman rank correlation coecient; trend analysis; soil; groundwater. Environmental forensic investigations can involve a The idea behind the rank correlation coecient is variety of statistical analysis techniques. A relatively simple. Each variable is ranked separately from lowest simple technique that can be used for exploratory data to highest e.g. 1, 2, 3, etc.) and the dierence between analysis is the Spearman rank correlation coecient. In ranks for each data pair is recorded. If the data are this technical note, I describe howthe Spearman rank correlated, then the sum of the square of the dierence correlation coecient can be used as a statistical tool between ranks will be small. The magnitude of the sum to detect monotonic trends in chemical concentrations is related to the signi®cance of the correlation. with time or space. The Spearman rank correlation coecient is calcu- Trend analysis can be useful for detecting chemical lated according to the following equation: ``footprints'' at a site or evaluating the eectiveness of Pn an installed or natural attenuation remedy.
    [Show full text]
  • One Sample T Test
    Copyright c October 17, 2020 by NEH One Sample t Test Nathaniel E. Helwig University of Minnesota 1 How Beer Changed the World William Sealy Gosset was a chemist and statistician who was employed as the Head Exper- imental Brewer at Guinness in the early 1900s. As a part of his job, Gosset was responsible for taking samples of beer and performing various analyses to ensure that the beer was of the proper composition and quality. While at Guinness, Gosset taught himself experimental design and statistical analysis (which were new and exciting fields at the time), and he even spent some time in 1906{1907 studying in Karl Pearson's laboratory. Gosset's work often involved collecting a small number of samples, and testing hypotheses about the mean of the population from which the samples were drawn. For example, in the brewery, Gosset may want to test whether the population mean amount of some ingredient (e.g., barley) was equal to the intended value. And, on the farm, Gosset may want to test how different farming techniques and growing conditions affect the barley yields. Through this work, Gos- set noticed that the normal distribution was not adequate for testing hypotheses about the mean in small samples of data with an unknown variance. 2 2 1 Pn As a reminder, if X ∼ N(µ, σ ), thenx ¯ ∼ N(µ, σ =n) wherex ¯ = n i=1 xi, which implies x¯ − µ Z = p ∼ N(0; 1) σ= n i.e., the Z test statistic follows a standard normal distribution. However, in practice, the 2 2 1 Pn 2 population variance σ is often unknown, so the sample variance s = n−1 i=1(xi − x¯) must be used in its place.
    [Show full text]
  • Nonparametric Estimation by Convex Programming
    The Annals of Statistics 2009, Vol. 37, No. 5A, 2278–2300 DOI: 10.1214/08-AOS654 c Institute of Mathematical Statistics, 2009 NONPARAMETRIC ESTIMATION BY CONVEX PROGRAMMING By Anatoli B. Juditsky and Arkadi S. Nemirovski1 Universit´eGrenoble I and Georgia Institute of Technology The problem we concentrate on is as follows: given (1) a convex compact set X in Rn, an affine mapping x 7→ A(x), a parametric family {pµ(·)} of probability densities and (2) N i.i.d. observations of the random variable ω, distributed with the density pA(x)(·) for some (unknown) x ∈ X, estimate the value gT x of a given linear form at x. For several families {pµ(·)} with no additional assumptions on X and A, we develop computationally efficient estimation routines which are minimax optimal, within an absolute constant factor. We then apply these routines to recovering x itself in the Euclidean norm. 1. Introduction. The problem we are interested in is essentially as fol- lows: suppose that we are given a convex compact set X in Rn, an affine mapping x A(x) and a parametric family pµ( ) of probability densities. Suppose that7→N i.i.d. observations of the random{ variable· } ω, distributed with the density p ( ) for some (unknown) x X, are available. Our objective A(x) · ∈ is to estimate the value gT x of a given linear form at x. In nonparametric statistics, there exists an immense literature on various versions of this problem (see, e.g., [10, 11, 12, 13, 15, 17, 18, 21, 22, 23, 24, 25, 26, 27, 28] and the references therein).
    [Show full text]
  • Repeated-Measures ANOVA & Friedman Test Using STATCAL
    Repeated-Measures ANOVA & Friedman Test Using STATCAL (R) & SPSS Prana Ugiana Gio Download STATCAL in www.statcal.com i CONTENT 1.1 Example of Case 1.2 Explanation of Some Book About Repeated-Measures ANOVA 1.3 Repeated-Measures ANOVA & Friedman Test 1.4 Normality Assumption and Assumption of Equality of Variances (Sphericity) 1.5 Descriptive Statistics Based On SPSS dan STATCAL (R) 1.6 Normality Assumption Test Using Kolmogorov-Smirnov Test Based on SPSS & STATCAL (R) 1.7 Assumption Test of Equality of Variances Using Mauchly Test Based on SPSS & STATCAL (R) 1.8 Repeated-Measures ANOVA Based on SPSS & STATCAL (R) 1.9 Multiple Comparison Test Using Boferroni Test Based on SPSS & STATCAL (R) 1.10 Friedman Test Based on SPSS & STATCAL (R) 1.11 Multiple Comparison Test Using Wilcoxon Test Based on SPSS & STATCAL (R) ii 1.1 Example of Case For example given data of weight of 11 persons before and after consuming medicine of diet for one week, two weeks, three weeks and four week (Table 1.1.1). Tabel 1.1.1 Data of Weight of 11 Persons Weight Name Before One Week Two Weeks Three Weeks Four Weeks A 89.43 85.54 80.45 78.65 75.45 B 85.33 82.34 79.43 76.55 71.35 C 90.86 87.54 85.45 80.54 76.53 D 91.53 87.43 83.43 80.44 77.64 E 90.43 84.45 81.34 78.64 75.43 F 90.52 86.54 85.47 81.44 78.64 G 87.44 83.34 80.54 78.43 77.43 H 89.53 86.45 84.54 81.35 78.43 I 91.34 88.78 85.47 82.43 78.76 J 88.64 84.36 80.66 78.65 77.43 K 89.51 85.68 82.68 79.71 76.5 Average 89.51 85.68 82.68 79.71 76.69 Based on Table 1.1.1: The person whose name is A has initial weight 89,43, after consuming medicine of diet for one week 85,54, two weeks 80,45, three weeks 78,65 and four weeks 75,45.
    [Show full text]
  • 7 Nonparametric Methods
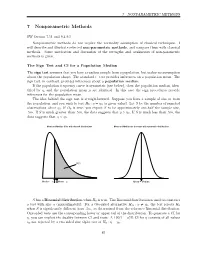
    7 NONPARAMETRIC METHODS 7 Nonparametric Methods SW Section 7.11 and 9.4-9.5 Nonparametric methods do not require the normality assumption of classical techniques. I will describe and illustrate selected non-parametric methods, and compare them with classical methods. Some motivation and discussion of the strengths and weaknesses of non-parametric methods is given. The Sign Test and CI for a Population Median The sign test assumes that you have a random sample from a population, but makes no assumption about the population shape. The standard t−test provides inferences on a population mean. The sign test, in contrast, provides inferences about a population median. If the population frequency curve is symmetric (see below), then the population median, iden- tified by η, and the population mean µ are identical. In this case the sign procedures provide inferences for the population mean. The idea behind the sign test is straightforward. Suppose you have a sample of size m from the population, and you wish to test H0 : η = η0 (a given value). Let S be the number of sampled observations above η0. If H0 is true, you expect S to be approximately one-half the sample size, .5m. If S is much greater than .5m, the data suggests that η > η0. If S is much less than .5m, the data suggests that η < η0. Mean and Median differ with skewed distributions Mean and Median are the same with symmetric distributions 50% Median = η Mean = µ Mean = Median S has a Binomial distribution when H0 is true. The Binomial distribution is used to construct a test with size α (approximately).
    [Show full text]
  • Correlation • References: O Kendall, M., 1938: a New Measure of Rank Correlation
    Coupling metrics to diagnose land-atmosphere interactions http://tiny.cc/l-a-metrics Correlation • References: o Kendall, M., 1938: A new measure of rank correlation. Biometrika, 30(1-2), 81–89. o Pearson, K., 1895: Notes on regression and inheritance in the case of two parents, Proc. Royal Soc. London, 58, 240–242. o Spearman, C., 1907, Demonstration of formulæ for true measurement of correlation. Amer. J. Psychol., 18(2), 161–169. • Principle: o A correlation r is a measure of how one variable tends to vary (in sync, out of sync, or randomly) with another variable in space and/or time. –1 ≤ r ≤ 1 o The most commonly used is Pearson product-moment correlation coefficient, which relates how well a distribution of two quantities fits a linear regression: cov(x, y) xy− x y r(x, y) = = 2 2 σx σy x xx y yy − − where overbars denote averages over domains in space, time or both. § As with linear regressions, there is an implied assumption that the distribution of each variable is near normal. If one or both variables are not, it may be advisable to remap them into a normal distribution. o Spearman's rank correlation coefficient relates the ranked ordering of two variables in a non-parametric fashion. This can be handy as Pearson’s r can be heavily influenced by outliers, just as linear regressions are. The equation is the same but the sorted ranks of x and y are used instead of the values of x and y. o Kendall rank correlation coefficient is a variant of rank correlation.
    [Show full text]
  • 9 Blocked Designs
    9 Blocked Designs 9.1 Friedman's Test 9.1.1 Application 1: Randomized Complete Block Designs • Assume there are k treatments of interest in an experiment. In Section 8, we considered the k-sample Extension of the Median Test and the Kruskal-Wallis Test to test for any differences in the k treatment medians. • Suppose the experimenter is still concerned with studying the effects of a single factor on a response of interest, but variability from another factor that is not of interest is expected. { Suppose a researcher wants to study the effect of 4 fertilizers on the yield of cotton. The researcher also knows that the soil conditions at the 8 areas for performing an experiment are highly variable. Thus, the researcher wants to design an experiment to detect any differences among the 4 fertilizers on the cotton yield in the presence a \nuisance variable" not of interest (the 8 areas). • Because experimental units can vary greatly with respect to physical characteristics that can also influence the response, the responses from experimental units that receive the same treatment can also vary greatly. • If it is not controlled or accounted for in the data analysis, it can can greatly inflate the experimental variability making it difficult to detect real differences among the k treatments of interest (large Type II error). • If this source of variability can be separated from the treatment effects and the random experimental error, then the sensitivity of the experiment to detect real differences between treatments in increased (i.e., lower the Type II error). • Therefore, the goal is to choose an experimental design in which it is possible to control the effects of a variable not of interest by bringing experimental units that are similar into a group called a \block".
    [Show full text]
  • Correlation and Regression Analysis
    OIC ACCREDITATION CERTIFICATION PROGRAMME FOR OFFICIAL STATISTICS Correlation and Regression Analysis TEXTBOOK ORGANISATION OF ISLAMIC COOPERATION STATISTICAL ECONOMIC AND SOCIAL RESEARCH AND TRAINING CENTRE FOR ISLAMIC COUNTRIES OIC ACCREDITATION CERTIFICATION PROGRAMME FOR OFFICIAL STATISTICS Correlation and Regression Analysis TEXTBOOK {{Dr. Mohamed Ahmed Zaid}} ORGANISATION OF ISLAMIC COOPERATION STATISTICAL ECONOMIC AND SOCIAL RESEARCH AND TRAINING CENTRE FOR ISLAMIC COUNTRIES © 2015 The Statistical, Economic and Social Research and Training Centre for Islamic Countries (SESRIC) Kudüs Cad. No: 9, Diplomatik Site, 06450 Oran, Ankara – Turkey Telephone +90 – 312 – 468 6172 Internet www.sesric.org E-mail [email protected] The material presented in this publication is copyrighted. The authors give the permission to view, copy download, and print the material presented that these materials are not going to be reused, on whatsoever condition, for commercial purposes. For permission to reproduce or reprint any part of this publication, please send a request with complete information to the Publication Department of SESRIC. All queries on rights and licenses should be addressed to the Statistics Department, SESRIC, at the aforementioned address. DISCLAIMER: Any views or opinions presented in this document are solely those of the author(s) and do not reflect the views of SESRIC. ISBN: xxx-xxx-xxxx-xx-x Cover design by Publication Department, SESRIC. For additional information, contact Statistics Department, SESRIC. i CONTENTS Acronyms
    [Show full text]