Why the Kidney Glomerulus Does Not Clog: a Gel Permeation Diffusion Hypothesis of Renal Function
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Calcium Phosphate Microcrystals in the Renal Tubular Fluid Accelerate Chronic Kidney Disease Progression
The Journal of Clinical Investigation RESEARCH ARTICLE Calcium phosphate microcrystals in the renal tubular fluid accelerate chronic kidney disease progression Kazuhiro Shiizaki,1,2 Asako Tsubouchi,3 Yutaka Miura,1 Kinya Seo,4 Takahiro Kuchimaru,5 Hirosaka Hayashi,1 Yoshitaka Iwazu,1,6,7 Marina Miura,1,6 Batpurev Battulga,8 Nobuhiko Ohno,8,9 Toru Hara,10 Rina Kunishige,3 Mamiko Masutani,11 Keita Negishi,12 Kazuomi Kario,12 Kazuhiko Kotani,7 Toshiyuki Yamada,7 Daisuke Nagata,6 Issei Komuro,13 Hiroshi Itoh,14 Hiroshi Kurosu,1 Masayuki Murata,3 and Makoto Kuro-o1 1Division of Anti-aging Medicine, Center for Molecular Medicine, Jichi Medical University, Shimotsuke, Japan. 2Yurina Medical Park, Shimotsuga, Japan. 3Graduate School of Arts and Sciences, University of Tokyo, Tokyo, Japan. 4Division of Cell and Molecular Medicine, 5Division of Cardiology and Metabolism, Center for Molecular Medicine, 6Division of Nephrology, Department of Internal Medicine, 7Department of Clinical Laboratory Medicine, and 8Division of Histology and Cell Biology, Department of Anatomy, Jichi Medical University, Shimotsuke, Japan. 9Division of Ultrastructural Research, National Institute for Physiological Sciences, Okazaki, Japan. 10Electron Microscopy Analysis Station, Research Network and Facility Service Division, National Institute for Materials Science, Tsukuba, Japan. 11Healthcare Business Unit, Nikon Corporation, Yokohama, Japan. 12Division of Cardiovascular Medicine, Department of Internal Medicine, Jichi Medical University, Shimotsuke, Japan. 13Department of Cardiovascular Medicine, Graduate School of Medicine, University of Tokyo, Tokyo, Japan. 14Division of Endocrinology, Metabolism and Nephrology, Department of Internal Medicine, Keio University School of Medicine, Tokyo, Japan. The Western pattern diet is rich not only in fat and calories but also in phosphate. -

« Glomerulogenesis and Renal Tubular Differentiation : Role of Hnf1β »
THESE DE DOCTORAT DE L’UNIVERSITE PARIS DESCARTES Ecole doctorale « Bio Sorbonne Paris Cité », ED 562 Département Développement, Génétique, Reproduction, Neurobiologie et Vieillissement (DGRNV) Spécialité : Développement Présentée pour obtenir le titre de DOCTEUR de l’Université Paris Descartes « Glomerulogenesis and renal tubular differentiation : Role of HNF1 β » Par Mlle Arianna FIORENTINO Soutenance le 13 décembre 2016 Composition du jury : Mme. Evelyne Fischer Directrice de thèse M. Marco Pontoglio Examinateur M. Jean-Jacques Boffa Rapporteur M. Yves Allory Rapporteur M Rémi Salomon Examinateur M Jean-Claude Dussaule Examinateur Equipe "Expression Génique, Développement et Maladies" (EGDM) INSERM U1016/ CNRS UMR 8104 / Université Paris-Descartes Institut Cochin, Dpt. Développement, Reproduction et Cancer 24, Rue du Faubourg Saint Jacques, 75014 Paris, France A. Fiorentino HNF1beta in kidney development “Connaître ce n'est pas démontrer, ni expliquer. C'est accéder à la vision.” (Le Petit Prince- Antoine de Saint-Exupéry) 2 A. Fiorentino HNF1beta in kidney development Aknowledgments - Remerciements – Ringraziamenti During this long adventure of the PhD, I was surrounded by many people that I will try to thank to in these pages. In first place, I would like to thank the members of the jury that have kindly accepted to evaluate my work: Jean-Jacques Boffa, Yves Allory, Jean-Claude Dussaule and Rémi Salomon. For the supervision and the precious advices, I would like to thank Evelyne Fischer and Marco Pontoglio that overviewed all my work. I thank Evelyne, my thesis director, for the scientific exchanges of ideas, for the guidance to complete my project and for her help in difficult moments. I thank Marco for the discussions, even for the heated ones, because the pressure in the environment not only helped me to work harder on science but more importantly on my character, to face the problems and solve them. -
Urinary System
OUTLINE 27.1 General Structure and Functions of the Urinary System 818 27.2 Kidneys 820 27 27.2a Gross and Sectional Anatomy of the Kidney 820 27.2b Blood Supply to the Kidney 821 27.2c Nephrons 824 27.2d How Tubular Fluid Becomes Urine 828 27.2e Juxtaglomerular Apparatus 828 Urinary 27.2f Innervation of the Kidney 828 27.3 Urinary Tract 829 27.3a Ureters 829 27.3b Urinary Bladder 830 System 27.3c Urethra 833 27.4 Aging and the Urinary System 834 27.5 Development of the Urinary System 835 27.5a Kidney and Ureter Development 835 27.5b Urinary Bladder and Urethra Development 835 MODULE 13: URINARY SYSTEM mck78097_ch27_817-841.indd 817 2/25/11 2:24 PM 818 Chapter Twenty-Seven Urinary System n the course of carrying out their specific functions, the cells Besides removing waste products from the bloodstream, the uri- I of all body systems produce waste products, and these waste nary system performs many other functions, including the following: products end up in the bloodstream. In this case, the bloodstream is ■ Storage of urine. Urine is produced continuously, but analogous to a river that supplies drinking water to a nearby town. it would be quite inconvenient if we were constantly The river water may become polluted with sediment, animal waste, excreting urine. The urinary bladder is an expandable, and motorboat fuel—but the town has a water treatment plant that muscular sac that can store as much as 1 liter of urine. removes these waste products and makes the water safe to drink. -
![L8-Urine Conc. [PDF]](https://docslib.b-cdn.net/cover/4402/l8-urine-conc-pdf-1384402.webp)
L8-Urine Conc. [PDF]
The loop of Henle is referred to as countercurrent multiplier and vasa recta as countercurrent exchange systems in concentrating and diluting urine. Explain what happens to osmolarity of tubular fluid in the various segments of the loop of Henle when concentrated urine is being produced. Explain the factors that determine the ability of loop of Henle to make a concentrated medullary gradient. Differentiate between water diuresis and osmotic diuresis. Appreciate clinical correlates of diabetes mellitus and diabetes insipidus. Fluid intake The total body water Antidiuretic hormone is controled by : Renal excretion of water Hyperosmolar medullary Changes in the osmolarity of tubular fluid : interstitium 1 2 3 Low osmolarity The osmolarity High osmolarity because of active decrease as it goes up because of the transport of Na+ and because of the reabsorbation of water co-transport of K+ and reabsorption of NaCl Cl- 4 5 Low osmolarity because of High osmolarity because of reabsorption of NaCl , also reabsorption of water in reabsorption of water in present of ADH , present of ADH reabsorption of urea Mechanisms responsible for creation of hyperosmolar medulla: Active Co- Facilitated diffusion transport : transport : diffusion : of : Na+ ions out of the Only of small thick portion of the K+ , Cl- and other amounts of water ascending limb of ions out of the thick from the medullary the loop of henle portion of the Of urea from the tubules into the into the medullary ascending limb of inner medullary medullary interstitium the loop of henle collecting -

A Study of the Effect of Protein in Tubular Fluid in Proximal Tubular Reabsorption Robert Lee Mitchell Yale University
Yale University EliScholar – A Digital Platform for Scholarly Publishing at Yale Yale Medicine Thesis Digital Library School of Medicine 1964 A study of the effect of protein in tubular fluid in proximal tubular reabsorption Robert Lee Mitchell Yale University Follow this and additional works at: http://elischolar.library.yale.edu/ymtdl Recommended Citation Mitchell, Robert Lee, "A study of the effect of protein in tubular fluid in proximal tubular reabsorption" (1964). Yale Medicine Thesis Digital Library. 2943. http://elischolar.library.yale.edu/ymtdl/2943 This Open Access Thesis is brought to you for free and open access by the School of Medicine at EliScholar – A Digital Platform for Scholarly Publishing at Yale. It has been accepted for inclusion in Yale Medicine Thesis Digital Library by an authorized administrator of EliScholar – A Digital Platform for Scholarly Publishing at Yale. For more information, please contact [email protected]. YALE UNIVERSITY LIBRARY 3 9002 06679 0909 A STUDY OF THE EFFECT OF PROTEIN IN TUBULAR FLUID IN OXIMAL TUBULAR REABSORPTION ROBERT L. MITCHELL 19 6 4 YALE MEDICAL LIBRARY Digitized by the Internet Archive in 2017 with funding from The National Endowment for the Humanities and the Arcadia Fund https://archive.org/details/studyofeffectofpOOmitc A STUDY OF THE EFFECT OF PROTEIN IN TUBULAR FLUID IN PROXIMAL TUBULAR REABSORPTION by Robert L, Mitchell (B.A. DePauw I960) A Thesis Presented to the Faculty of the Yale University School of Medicine in Partial Fulfillment of the Requirements for the Degree of Doctor of Medicine Yale University School of Medicine 196U ACKNOWLEDGMENT With sincere appreciation* I wish to express my gratitude to Dr. -

The Distal Convoluted Tubule and Collecting Duct
Chapter 23 *Lecture PowerPoint The Urinary System *See separate FlexArt PowerPoint slides for all figures and tables preinserted into PowerPoint without notes. Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Introduction • Urinary system rids the body of waste products. • The urinary system is closely associated with the reproductive system – Shared embryonic development and adult anatomical relationship – Collectively called the urogenital (UG) system 23-2 Functions of the Urinary System • Expected Learning Outcomes – Name and locate the organs of the urinary system. – List several functions of the kidneys in addition to urine formation. – Name the major nitrogenous wastes and identify their sources. – Define excretion and identify the systems that excrete wastes. 23-3 Functions of the Urinary System Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Diaphragm 11th and 12th ribs Adrenal gland Renal artery Renal vein Kidney Vertebra L2 Aorta Inferior vena cava Ureter Urinary bladder Urethra Figure 23.1a,b (a) Anterior view (b) Posterior view • Urinary system consists of six organs: two kidneys, two ureters, urinary bladder, and urethra 23-4 Functions of the Kidneys • Filters blood plasma, separates waste from useful chemicals, returns useful substances to blood, eliminates wastes • Regulate blood volume and pressure by eliminating or conserving water • Regulate the osmolarity of the body fluids by controlling the relative amounts of water and solutes -

Filtration of Protein in the Anti-Glomerular Basement Membrane Nephritic Rat: a Micropuncture Study
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Kidney International, Vol. 10 (1976) p. 425—437 Filtration of protein in the anti-glomerular basement membrane nephritic rat: A micropuncture study HANS VON BAEYER, JUDITH B. VAN LIEW, JOHN KLASSEN and JOHN W. BOYLAN with the technical assistance of NANCY MANZ and PATRICIA MUIR Departments of Medicine, Physiology and Microbiology, State University of New York at Buffalo and Veterans Administration Hospital, Buffalo, New York Filtration of protein in the anti-glomerular basement membrane (GBM). We have used this animal model to examine, nephritic rat: A micropuncture study. Production on an anti-gb- with micropuncture techniques, changes in the filtra- merular basement membrane (anti-GBM) nephritis in the rat re- sults in a 30-fold increase in glomerular membrane permeability to tion and reabsorption of protein during the first to albumin. The concentration of albumin in glomerular filtrate, esti- third weeks of the disease (days 2 to 17) and to mated from proximal tubular fluid samples, is ten times the normal correlate some of the renal functional deficits ob- value. Tubular reabsorption of albumin is not enhanced so that essentially the filtered load is excreted. A nephrotic syndrome served with pathological findings. The period of develops rapidly. Total kidney gbomerular filtration rate (GFR) is study therefore complements the work of Baldamus reduced to 40% of normal with a proportional reduction in filtra- et al [1] on changes in protein excretion during the tion fraction. Glomerulo-tubular balance is maintained since prox- imal fractional reabsorption remains constant near control levels. -
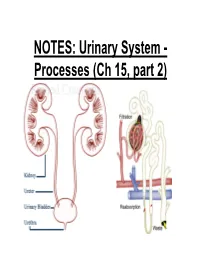
NOTES: Urinary System
NOTES: Urinary System - Processes (Ch 15, part 2) *Recall: the primary function of the urinary system is to filter the blood of ions and nitrogenous wastes; when combined with water, these wastes make up URINE. • Kidneys receive about 20-25% of total cardiac output – ~1200mL of blood goes through the kidneys per minute Blood Supply to Kidneys • Descending aorta Renal artery interlobar arcuate cortical afferent arterioles • The afferent arterioles deliver blood to nephrons NEPHRONS • NEPHRONS: the functional units of the kidneys -each kidney contains about a million nephrons! Parts of a NEPHRON: • GLOMERULUS: tangled cluster of blood capillaries • GLOMERULAR CAPSULE (a.k.a. Bowman’s capsule): thin-walled structure surrounding glomerulus Parts of a NEPHRON: • PROXIMAL CONVOLUTED TUBULE • LOOP OF HENLE -descending limb -ascending limb • DISTAL CONVOLUTED TUBULE Parts of a NEPHRON: • COLLECTING DUCT (where distal tubules from several nephrons converge and drain into; from here, urine empties into the RENAL PELVIS) Blood Supply of a Nephron: -blood is brought to a nephron from an afferent arteriole; -from here, it is passed to an efferent arteriole; -this gives rise to a system of peritubular capillaries that surround the renal tubules URINE FORMATION *nephrons remove wastes from blood and regulate water and electrolyte concentrations. URINE IS THE END PRODUCT! Three Organic Wastes Products of Urine 1) Urea: most abundant, from breakdown of amino acids 2) Creatinine: generated in skeletal muscle when creatine phosphate is broken down (creatine -
Osmolality of Distal Tubular Fluid in the Dog
Osmolality of distal tubular fluid in the dog. J R Clapp, R R Robinson J Clin Invest. 1966;45(12):1847-1853. https://doi.org/10.1172/JCI105488. Research Article Find the latest version: https://jci.me/105488/pdf Journal of Clinical Investigation Vol. 45, No. 12, 1966 Osmolality of Distal Tubular Fluid in the Dog * JAMES R. CLAPP t AND ROSCOE R. ROBINSON t (From the Department of Medicine, Duke University Medical Center, Durham, N. C.) Renal micropuncture observations in rodents suggested that dog distal fluid is normally hypo- have demonstrated that the tubular fluid from early tonic rather than isotonic at the end of the distal portions of the distal convoluted tubule is always convolution. If so, at high rates of urine flow dur- hypotonic to plasma (1, 2). A limited number of ing osmotic diuresis, the ability of the collecting observations have suggested that its hypotonicity ducts to abstract solute-free water might be so is maintained along the entire distal tubule dur- exceeded that hypotonic urine could be excreted ing water diuresis (1). In contrast, during hy- despite the presence of antidiuretic hormone. dropenia with or without a superimposed osmotic Possible relationships among rates of solute excre- diuresis, the distal fluid achieves osmotic equi- tion, vasopressin dosage, and solute-free water librium with plasma in later portions of the distal reabsorption by the collecting ducts have been tubule (1, 2). Consequently, in the presence of discussed fully by Orloff, Wagner, and Davidson antidiuretic hormone, it has been widely accepted (11). that distal tubular fluid is always isosmotic to Heretofore, direct measurements of distal fluid plasma as it enters the cortical collecting ducts. -

A High-Powered View of the Filtration Barrier
SPECIAL ARTICLE www.jasn.org A High-Powered View of the Filtration Barrier Ja´nos Peti-Peterdi and Arnold Sipos Departments of Physiology and Biophysics and Medicine, Zilkha Neurogenetic Institute, University of Southern California, Los Angeles, California ABSTRACT Multiphoton excitation fluorescence microscopy is a powerful noninvasive imaging (PAN) model of focal segmental glo- technique for the deep optical sectioning of living tissues. Its application in several merulosclerosis (FSGS). intact tissues is a significant advance in our understanding of organ function, including renal pathophysiological mechanisms. The glomerulus, the filtering unit in the kidney, is one good example of a relatively inaccessible and complex structure, MULTIPHOTON IMAGING SHOWS with cell types that are otherwise difficult to study at high resolution in their native NEW DETAILS OF environment. In this article, we address the application, advantages, and limita- JUXTAGLOMERULAR FUNCTION tions of this imaging technology for the study of the glomerular filtration barrier and the controversy it recently generated regarding the glomerular filtration of One of the main research interests of our macromolecules. More advanced and accurate multiphoton determinations of the laboratory has been the function of the glomerular sieving coefficient that are presented here dismiss previous claims on juxtaglomerular apparatus (JGA), the the filtration of nephrotic levels of albumin. The sieving coefficient of 70-kD mechanisms of basic physiologic pro- dextran was found to be around 0.001. Using a model of focal segmental glomer- cesses by which cells of the macula densa ulosclerosis, increased filtration barrier permeability is restricted only to areas of in the distal nephron control GFR, renal podocyte damage, consistent with the generally accepted role of podocytes and blood flow, and the renin–angiotensin the glomerular origin of albuminuria. -

Fig. 8.1. Glomerular Filtration Barrier. the Glomerular Filtration Barrier
Fig. 8.1. Glomerular filtration barrier. The glomerular filtration barrier consists of the capillary endothelial cell, the glomerular basement membrane, and the epithelial cells (podocytes). H2O and most solutes pass through fenestrations in the endothelial cells, through a semipermeable basement membrane, through the slit pores between the foot processes of the podocytes, into Bowman’s space, and then into the proximal renal tubule. Fig. 8.2. Major physiologic processes of renal tubules that pertain to solutes and H2O. The solute concentrations are provided to illustrate changes that occur as the fluid moves through the nephron (see Fig. 8.3). Actual solute concentrations would vary, depending on many physiologic and pathologic factors. Fig. 8.2. continued • The osmolality of the plasma and the ultrafiltrate are equal (near 300 mmol/kg) as H2O and nonprotein solutes pass through the glomerular filtration barrier. • In the proximal tubules, a majority of the H2O and solutes that enter the tubules are resorbed through active, facilitated, and passive processes. The osmolality of the tubular fluid leaving the proximal tubule is still near 300 mmol/kg, but the fluid volume is greatly diminished. • In the descending limb of the loop of Henle, tubular fluid is concentrated and volume reduced by the passive movement of 2H O. Urea may diffuse from the interstitial fluid to the tubular fluid. At the bottom of the loop of Henle, the concentration of the tubular fluid will vary among species. The 1500 mmol/kg value is probably appropriate for horses and cattle, whereas the solute concentration in cats may be > 2400 mmol/kg. -
The Urinary System
24 The Urinary System Lecture Presentation by Lori Garrett © 2018 Pearson Education, Inc. Section 1: Anatomy of the Urinary System Learning Outcomes 24.1 Identify the organs of the urinary system, and cite a primary function of each. 24.2 Describe the location and structural features of the kidneys. 24.3 Describe the gross structural features of the kidney, and distinguish between cortical and juxtamedullary nephrons. © 2018 Pearson Education, Inc. Section 1: Anatomy of the Urinary System Learning Outcomes (continued) 24.4 Describe the segments of the nephron and collecting system, including their general functions and histological appearance. 24.5 Trace the pathway of blood flow through a kidney, and compare the pattern of blood flow in cortical and juxtamedullary nephrons. © 2018 Pearson Education, Inc. Module 24.1: The urinary system organs are the kidneys, ureters, urinary bladder, and urethra Urinary system . Two kidneys • Receive 25 percent of the cardiac output • Major excretory organs of the urinary system • Produce urine (fluid containing water, ions, and small soluble substances) © 2018 Pearson Education, Inc. Module 24.1: Urinary system organs Urinary tract . Ureters—receive urine from the kidneys • Conduct urine to the urinary bladder by gravity and peristalsis . Urinary bladder—receives and stores urine • Contraction of muscle in walls drives urination . Urethra—conducts urine from the bladder to outside the body © 2018 Pearson Education, Inc. © 2018 Pearson Education, Inc. Module 24.1: Review A. Name the major excretory organs of the urinary system. B. Describe the functions of the urinary system. Learning Outcome: Identify the organs of the urinary system, and cite a primary function of each.