Lecture 5 Potential Temperature and Density Neutral
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Potential Vorticity
POTENTIAL VORTICITY Roger K. Smith March 3, 2003 Contents 1 Potential Vorticity Thinking - How might it help the fore- caster? 2 1.1Introduction............................ 2 1.2WhatisPV-thinking?...................... 4 1.3Examplesof‘PV-thinking’.................... 7 1.3.1 A thought-experiment for understanding tropical cy- clonemotion........................ 7 1.3.2 Kelvin-Helmholtz shear instability . ......... 9 1.3.3 Rossby wave propagation in a β-planechannel..... 12 1.4ThestructureofEPVintheatmosphere............ 13 1.4.1 Isentropicpotentialvorticitymaps........... 14 1.4.2 The vertical structure of upper-air PV anomalies . 18 2 A Potential Vorticity view of cyclogenesis 21 2.1PreliminaryIdeas......................... 21 2.2SurfacelayersofPV....................... 21 2.3Potentialvorticitygradientwaves................ 23 2.4 Baroclinic Instability . .................... 28 2.5 Applications to understanding cyclogenesis . ......... 30 3 Invertibility, iso-PV charts, diabatic and frictional effects. 33 3.1 Invertibility of EPV ........................ 33 3.2Iso-PVcharts........................... 33 3.3Diabaticandfrictionaleffects.................. 34 3.4Theeffectsofdiabaticheatingoncyclogenesis......... 36 3.5Thedemiseofcutofflowsandblockinganticyclones...... 36 3.6AdvantageofPVanalysisofcutofflows............. 37 3.7ThePVstructureoftropicalcyclones.............. 37 1 Chapter 1 Potential Vorticity Thinking - How might it help the forecaster? 1.1 Introduction A review paper on the applications of Potential Vorticity (PV-) concepts by Brian -

Rapid Mixing and Exchange of Deep-Ocean Waters in an Abyssal Boundary Current
Rapid mixing and exchange of deep-ocean waters in an abyssal boundary current Alberto C. Naveira Garabatoa,1, Eleanor E. Frajka-Williamsb, Carl P. Spingysa, Sonya Leggc, Kurt L. Polzind, Alexander Forryana, E. Povl Abrahamsene, Christian E. Buckinghame, Stephen M. Griffiesc, Stephen D. McPhailb, Keith W. Nichollse, Leif N. Thomasf, and Michael P. Meredithe aOcean and Earth Science, National Oceanography Centre, University of Southampton, SO14 3ZH Southampton, United Kingdom; bNational Oceanography Centre, SO14 3ZH Southampton, United Kingdom; cNational Oceanic and Atmospheric Administration Geophysical Fluid Dynamics Laboratory & Atmospheric and Oceanic Sciences Program, Princeton University, Princeton, NJ 08544; dDepartment of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543; ePolar Oceans, British Antarctic Survey, CB3 0ET Cambridge, United Kingdom; and fDepartment of Earth System Science, Stanford University, Stanford, CA 94305 Edited by Eric Guilyardi, Laboratoire d’Océanographie et du Climat: Expérimentations et Approches Numériques, Institute Pierre Simon Laplace, Paris, France, and accepted by Editorial Board Member Jean Jouzel May 26, 2019 (received for review March 8, 2019) The overturning circulation of the global ocean is critically shaped UK–US Dynamics of the Orkney Passage Outflow (DynOPO) by deep-ocean mixing, which transforms cold waters sinking at high project (17), and consisted of two core elements: a series of fifteen latitudes into warmer, shallower waters. The effectiveness of mixing 6- to 128-km-long vessel-based sections of profile measurements in driving this transformation is jointly set by two factors: the crossing the boundary current at an unusually high horizontal – – ∼ intensity of turbulence near topography and the rate at which well- resolution (Fig. -

Chapter 2 Approximate Thermodynamics
Chapter 2 Approximate Thermodynamics 2.1 Atmosphere Various texts (Byers 1965, Wallace and Hobbs 2006) provide elementary treatments of at- mospheric thermodynamics, while Iribarne and Godson (1981) and Emanuel (1994) present more advanced treatments. We provide only an approximate treatment which is accept- able for idealized calculations, but must be replaced by a more accurate representation if quantitative comparisons with the real world are desired. 2.1.1 Dry entropy In an atmosphere without moisture the ideal gas law for dry air is p = R T (2.1) ρ d where p is the pressure, ρ is the air density, T is the absolute temperature, and Rd = R/md, R being the universal gas constant and md the molecular weight of dry air. If moisture is present there are minor modications to this equation, which we ignore here. The dry entropy per unit mass of air is sd = Cp ln(T/TR) − Rd ln(p/pR) (2.2) where Cp is the mass (not molar) specic heat of dry air at constant pressure, TR is a constant reference temperature (say 300 K), and pR is a constant reference pressure (say 1000 hPa). Recall that the specic heats at constant pressure and volume (Cv) are related to the gas constant by Cp − Cv = Rd. (2.3) A variable related to the dry entropy is the potential temperature θ, which is dened Rd/Cp θ = TR exp(sd/Cp) = T (pR/p) . (2.4) The potential temperature is the temperature air would have if it were compressed or ex- panded (without condensation of water) in a reversible adiabatic fashion to the reference pressure pR. -
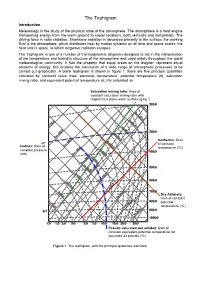
The Tephigram Introduction Meteorology Is the Study of the Physical State of the Atmosphere
The Tephigram Introduction Meteorology is the study of the physical state of the atmosphere. The atmosphere is a heat engine transporting energy from the warm ground to cooler locations, both vertically and horizontally. The driving force is solar radiation. Shortwave radiation is absorbed primarily at the surface; the working fluid is the atmosphere, which distributes heat by motion systems on all time and space scales; the heat sink is space, to which longwave radiation escapes. The Tephigram is one of a number of thermodynamic diagrams designed to aid in the interpretation of the temperature and humidity structure of the atmosphere and used widely throughout the world meteorological community. It has the property that equal areas on the diagram represent equal amounts of energy; this enables the calculation of a wide range of atmospheric processes to be carried out graphically. A blank tephigram is shown in figure 1; there are five principal quantities indicated by constant value lines: pressure, temperature, potential temperature (θ), saturation mixing ratio, and equivalent potential temperature (θe) for saturated air. Saturation mixing ratio: lines of constant saturation mixing ratio with respect to a plane water surface (g kg-1) Isotherms: lines of constant Isobars: lines of temperature (ºC) constant pressure (mb) Dry Adiabats: lines of constant potential temperature (ºC) Pseudo saturated wet adiabat: lines of constant equivalent potential temperature for saturated air parcels (ºC) Figure 1. The tephigram, with the principal quantities indicated. The principal axes of a tephigram are temperature and potential temperature; these are straight and perpendicular to each other, but rotated through about 45º anticlockwise so that lines of constant temperature run from bottom left to top right on the diagram. -

Hydrographic Atlas of the World Ocean Circulation Experiment (WOCE) Volume 2: Pacific Ocean
Hydrographic Atlas of the World Ocean Circulation Experiment (WOCE) Volume 2: Pacific Ocean Lynne D. Talley Series edited by Michael Sparrow, Piers Chapman and John Gould Hydrographic Atlas of the World Ocean Circulation Experiment (WOCE) Volume 2: Pacific Ocean Lynne D. Talley Scripps Institution of Oceanography, University of San Diego, La Jolla, California, USA. Series edited by Michael Sparrow, Piers Chapman and John Gould. Compilation funded by the US National Science Foundation, Ocean Science division grant OCE-9712209. Publication supported by BP. Cover Picture: The photo on the front cover was kindly supplied by Akihisa Otsuki. It shows squalls in the northernmost area of the Mariana Islands and was taken on June 12, 1993. Cover design: Signature Design in association with the atlas editors, Principal Investigators and BP. Printed by: ATAR Roto Presse SA, Geneva,Switzerland. DVD production: ODS Business Services Limited, Swindon, UK. Published by: National Oceanography Centre, Southampton, UK. Recommended form of citation: 1. For this volume: Talley, L. D., Hydrographic Atlas of the World Ocean Circulation Experiment (WOCE). Volume 2: Pacific Ocean (eds. M. Sparrow, P. Chapman and J. Gould), International WOCE Project Office, Southampton, UK, ISBN 0-904175-54-5. 2007 2. For the whole series: Sparrow, M., P. Chapman, J. Gould (eds.), The World Ocean Circulation Experiment (WOCE) Hydrographic Atlas Series (4 vol- umes), International WOCE Project Office, Southampton, UK, 2005-2007 WOCE is a project of the World Climate Research Programme (WCRP) which is sponsored by the World Meteorological Organization (WMO), the International Council for Science (ICSU) and the Intergovernmental Oceanographic Commission (IOC) of UNESCO. -

Gibbs Seawater (GSW) Oceanographic Toolbox of TEOS–10
Gibbs SeaWater (GSW) Oceanographic Toolbox of TEOS–10 documentation set density and enthalpy, based on the 48-term expression for density, gsw_front_page front page to the GSW Oceanographic Toolbox The functions in this group ending in “_CT” may also be called without “_CT”. gsw_contents contents of the GSW Oceanographic Toolbox gsw_check_functions checks that all the GSW functions work correctly gsw_rho_CT in-situ density, and potential density gsw_demo demonstrates many GSW functions and features gsw_alpha_CT thermal expansion coefficient with respect to CT gsw_beta_CT saline contraction coefficient at constant CT Practical Salinity (SP), PSS-78 gsw_rho_alpha_beta_CT in-situ density, thermal expansion & saline contraction coefficients gsw_specvol_CT specific volume gsw_SP_from_C Practical Salinity from conductivity, C (incl. for SP < 2) gsw_specvol_anom_CT specific volume anomaly gsw_C_from_SP conductivity, C, from Practical Salinity (incl. for SP < 2) gsw_sigma0_CT sigma0 from CT with reference pressure of 0 dbar gsw_SP_from_R Practical Salinity from conductivity ratio, R (incl. for SP < 2) gsw_sigma1_CT sigma1 from CT with reference pressure of 1000 dbar gsw_R_from_SP conductivity ratio, R, from Practical Salinity (incl. for SP < 2) gsw_sigma2_CT sigma2 from CT with reference pressure of 2000 dbar gsw_SP_salinometer Practical Salinity from a laboratory salinometer (incl. for SP < 2) gsw_sigma3_CT sigma3 from CT with reference pressure of 3000 dbar gsw_sigma4_CT sigma4 from CT with reference pressure of 4000 dbar Absolute Salinity -

Dry Adiabatic Temperature Lapse Rate
ATMO 551a Fall 2010 Dry Adiabatic Temperature Lapse Rate As we discussed earlier in this class, a key feature of thick atmospheres (where thick means atmospheres with pressures greater than 100-200 mb) is temperature decreases with increasing altitude at higher pressures defining the troposphere of these planets. We want to understand why tropospheric temperatures systematically decrease with altitude and what the rate of decrease is. The first order explanation is the dry adiabatic lapse rate. An adiabatic process means no heat is exchanged in the process. For this to be the case, the process must be “fast” so that no heat is exchanged with the environment. So in the first law of thermodynamics, we can anticipate that we will set the dQ term equal to zero. To get at the rate at which temperature decreases with altitude in the troposphere, we need to introduce some atmospheric relation that defines a dependence on altitude. This relation is the hydrostatic relation we have discussed previously. In summary, the adiabatic lapse rate will emerge from combining the hydrostatic relation and the first law of thermodynamics with the heat transfer term, dQ, set to zero. The gravity side The hydrostatic relation is dP = −g ρ dz (1) which relates pressure to altitude. We rearrange this as dP −g dz = = α dP (2) € ρ where α = 1/ρ is known as the specific volume which is the volume per unit mass. This is the equation we will use in a moment in deriving the adiabatic lapse rate. Notice that € F dW dE g dz ≡ dΦ = g dz = g = g (3) m m m where Φ is known as the geopotential, Fg is the force of gravity and dWg is the work done by gravity. -

Introduction to Atmospheric Dynamics Chapter 2
Introduction to Atmospheric Dynamics Chapter 2 Paul A. Ullrich [email protected] Part 3: Buoyancy and Convection Vertical Structure This cooling with height is related to the dynamics of the atmosphere. The change of temperature with height is called the lapse rate. Defnition: The lapse rate is defned as the rate (for instance in K/km) at which temperature decreases with height. @T Γ ⌘@z Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate For a dry adiabatic, stable, hydrostatic atmosphere the potential temperature θ does not vary in the vertical direction: @✓ =0 @z In a dry adiabatic, hydrostatic atmosphere the temperature T must decrease with height. How quickly does the temperature decrease? R/cp p0 Note: Use ✓ = T p ✓ ◆ Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate The adiabac change in temperature with height is T @✓ @T g = + ✓ @z @z cp For dry adiabac, hydrostac atmosphere: @T g = Γd − @z cp ⌘ Defnition: The dry adiabatic lapse rate is defned as the g rate (for instance in K/km) at which the temperature of an Γd air parcel will decrease with height if raised adiabatically. ⌘ cp g 1 9.8Kkm− cp ⇡ Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate This profle should be very close to the adiabatic lapse rate in a dry atmosphere. Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Fundamentals Even in adiabatic motion, with no external source of heating, if a parcel moves up or down its temperature will change. • What if a parcel moves about a surface of constant pressure? • What if a parcel moves about a surface of constant height? If the atmosphere is in adiabatic balance, the temperature still changes with height. -

Spiciness Theory Revisited, with New Views on Neutral Density, Orthogonality, and Passiveness
Ocean Sci., 17, 203–219, 2021 https://doi.org/10.5194/os-17-203-2021 © Author(s) 2021. This work is distributed under the Creative Commons Attribution 4.0 License. Spiciness theory revisited, with new views on neutral density, orthogonality, and passiveness Rémi Tailleux Dept. of Meteorology, University of Reading, Earley Gate, RG6 6ET Reading, United Kingdom Correspondence: Rémi Tailleux ([email protected]) Received: 26 April 2020 – Discussion started: 20 May 2020 Revised: 8 December 2020 – Accepted: 9 December 2020 – Published: 28 January 2021 Abstract. This paper clarifies the theoretical basis for con- 1 Introduction structing spiciness variables optimal for characterising ocean water masses. Three essential ingredients are identified: (1) a As is well known, three independent variables are needed to material density variable γ that is as neutral as feasible, (2) a fully characterise the thermodynamic state of a fluid parcel in material state function ξ independent of γ but otherwise ar- the standard approximation of seawater as a binary fluid. The bitrary, and (3) an empirically determined reference function standard description usually relies on the use of a tempera- ξr(γ / of γ representing the imagined behaviour of ξ in a ture variable (such as potential temperature θ, in situ temper- notional spiceless ocean. Ingredient (1) is required because ature T , or Conservative Temperature 2), a salinity variable contrary to what is often assumed, it is not the properties im- (such as reference composition salinity S or Absolute Salin- posed on ξ (such as orthogonality) that determine its dynam- ity SA), and pressure p. -

Equations of Motion Using Thermodynamic Coordinates
2814 JOURNAL OF PHYSICAL OCEANOGRAPHY VOLUME 30 Equations of Motion Using Thermodynamic Coordinates ROLAND A. DE SZOEKE College of Oceanic and Atmospheric Sciences, Oregon State University, Corvallis, Oregon (Manuscript received 21 October 1998, in ®nal form 30 December 1999) ABSTRACT The forms of the primitive equations of motion and continuity are obtained when an arbitrary thermodynamic state variableÐrestricted only to be vertically monotonicÐis used as the vertical coordinate. Natural general- izations of the Montgomery and Exner functions suggest themselves. For a multicomponent ¯uid like seawater the dependence of the coordinate on salinity, coupled with the thermobaric effect, generates contributions to the momentum balance from the salinity gradient, multiplied by a thermodynamic coef®cient that can be com- pletely described given the coordinate variable and the equation of state. In the vorticity balance this term produces a contribution identi®ed with the baroclinicity vector. Only when the coordinate variable is a function only of pressure and in situ speci®c volume does the coef®cient of salinity gradient vanish and the baroclinicity vector disappear. This coef®cient is explicitly calculated and displayed for potential speci®c volume as thermodynamic coor- dinate, and for patched potential speci®c volume, where different reference pressures are used in various pressure subranges. Except within a few hundred decibars of the reference pressures, the salinity-gradient coef®cient is not negligible and ought to be taken into account in ocean circulation models. 1. Introduction perature surfaces is a potential for the acceleration ®eld, Potential temperature, the temperature a ¯uid parcel when friction is negligible. Because the gradient of this would have if removed adiabatically and reversibly from function gives the geostrophic ¯ow when it balances ambient pressure to a reference pressure, is a valuable Coriolis force, it is also called the geostrophic stream- concept in the study of the atmosphere and oceans. -

Recovery of Temperature, Salinity, and Potential Density from Ocean
PUBLICATIONS Journal of Geophysical Research: Oceans RESEARCH ARTICLE Recovery of temperature, salinity, and potential density from 10.1002/2013JC009662 ocean reflectivity Key Points: Berta Biescas1,2, Barry R. Ruddick1, Mladen R. Nedimovic3,4,5, Valentı Sallare`s2, Guillermo Bornstein2, Recovery of oceanic T, S, and and Jhon F. Mojica2 potential density from acoustic reflectivity data 1Department of Oceanography, Dalhousie University, Halifax, Nova Scotia, Canada, 2Department of Marine Geology, Thermal anomalies observations at 3 the Mediterranean tongue level Institut de Cie`ncies del Mar ICM-CSIC, Barcelona, Spain, Department of Earth’s Sciences, Dalhousie University, Halifax, 4 5 Comparison between acoustic Nova Scotia, Canada, Lamont-Doherty Earth Observatory of Columbia University, Palisades, New York, USA, University of reflectors in the ocean and isopycnals Texas Institute for Geophysics, Austin, Texas, USA Supporting Information: Methods Abstract This work explores a method to recover temperature, salinity, and potential density of the Supporting figures ocean using acoustic reflectivity data and time and space coincident expendable bathythermographs (XBT). The acoustically derived (vertical frequency >10 Hz) and the XBT-derived (vertical frequency <10 Hz) impe- Correspondence to: dances are summed in the time domain to form impedance profiles. Temperature (T) and salinity (S) are B. Biescas, then calculated from impedance using the international thermodynamics equations of seawater (GSW [email protected] TEOS-10) and an empirical T-S relation derived with neural networks; and finally potential density (q) is cal- culated from T and S. The main difference between this method and previous inversion works done from Citation: Biescas, B., B. R. Ruddick, M. R. real multichannel seismic reflection (MCS) data recorded in the ocean, is that it inverts density and it does Nedimovic, V. -

Eddy Activity Sensitivity to Changes in the Vertical Structure of Baroclinicity
APRIL 2016 Y U V A L A N D K A S P I 1709 Eddy Activity Sensitivity to Changes in the Vertical Structure of Baroclinicity JANNI YUVAL AND YOHAI KASPI Department of Earth and Planetary Sciences, Weizmann Institute of Science, Rehovot, Israel (Manuscript received 12 May 2015, in final form 25 October 2015) ABSTRACT The relation between the mean meridional temperature gradient and eddy fluxes has been addressed by several eddy flux closure theories. However, these theories give little information on the dependence of eddy fluxes on the vertical structure of the temperature gradient. The response of eddies to changes in the vertical structure of the temperature gradient is especially interesting since global circulation models suggest that as a result of greenhouse warming, the lower-tropospheric temperature gradient will decrease whereas the upper- tropospheric temperature gradient will increase. The effects of the vertical structure of baroclinicity on at- mospheric circulation, particularly on the eddy activity, are investigated. An idealized global circulation model with a modified Newtonian relaxation scheme is used. The scheme allows the authors to obtain a heating profile that produces a predetermined mean temperature profile and to study the response of eddy activity to changes in the vertical structure of baroclinicity. The results indicate that eddy activity is more sensitive to temperature gradient changes in the upper troposphere. It is suggested that the larger eddy sensitivity to the upper-tropospheric temperature gradient is a consequence of large baroclinicity concen- trated in upper levels. This result is consistent with a 1D Eady-like model with nonuniform shear showing more sensitivity to shear changes in regions of larger baroclinicity.