A Maximum Entropy Model of Phonotactics and Phonotactic Learning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Syllabic Consonants and Phonotactics Syllabic Consonants
Syllabic consonants and phonotactics Syllabic consonants Consonants that stand as the peak of the syllable, and perform the functions of vowels, are called syllabic consonants. For example, in words like sudden and saddle, the consonant [d] is followed by either the consonant [n] or [l] without a vowel intervening. The [n] of sadden and the [l] of saddle constitute the centre of the second, unstressed, syllable and are considered to be syllabic peaks. They typically occur in an unstressed syllable immediately following the alveolar consonants, [t, s, z] as well as [d]. Examples of syllabic consonants Cattle [kæțɬ] wrestle [resɬ] Couple [kʌpɬ] knuckle [nʌkɬ] Panel[pæņɬ] petal [petɬ] Parcel [pa:șɬ] pedal [pedɬ] It is not unusual to find two syllabic consonants together. Examples are: national [næʃņɬ] literal [litrɬ] visionary [viʒņri] veteran [vetrņ] Phonotactics Phonotactic constraints determine what sounds can be put together to form the different parts of a syllable in a language. Examples: English onsets /kl/ is okay: “clean” “clamp” /pl/ is okay: “play” “plaque” */tl/ is not okay: *tlay *tlamp. We don’t often have words that begin with /tl/, /dm/, /rk/, etc. in English. However, these combinations can occur in the middle or final positions. So, what is phonotactics? Phonotactics is part of the phonology of a language. Phonotactics restricts the possible sound sequences and syllable structures in a language. Phonotactic constraint refers to any specific restriction To understand phonotactics, one must first understand syllable structure. Permissible language structures Languages differ in permissible syllable structures. Below are some simplified examples. Hawaiian: V, CV Japanese: V, CV, CVC Korean: V, CV, CVC, VCC, CVCC English: V CV CCV CCCV VC CVC CCVC CCCVC VCC CVCC CCVCC CCCVCC VCCC CVCCC CCVCCC CCCVCCC English consonant clusters sequences English allows CC and CCC clusters in onsets and codas, but they are highly restricted. -

CONSONANT CLUSTER PHONOTACTICS: a PERCEPTUAL APPROACH by MARIE-HÉLÈNE CÔTÉ B.Sc. Sciences Économiques, Université De Montr
CONSONANT CLUSTER PHONOTACTICS: A PERCEPTUAL APPROACH by MARIE-HÉLÈNE CÔTÉ B.Sc. Sciences économiques, Université de Montréal (1987) Diplôme Relations Internationales, Institut d’Études Politiques de Paris (1990) D.E.A. Démographie économique, Institut d’Études Politiques de Paris (1991) M.A. Linguistique, Université de Montréal (1995) Submitted to the department of Linguistics and Philosophy in partial fulfillment of the requirement for the degree of DOCTOR OF PHILOSOPHY À ma mère et à mon bébé, at the qui nous ont quittés À Marielle et Émile, MASSACHUSETTS INSTITUTE OF TECHNOLOGY qui nous sont arrivés À Jean-Pierre, qui est toujours là September 2000 © 2000 Marie-Hélène Côté. All rights reserved. The author hereby grants to M.I.T. the permission to reproduce and to distribute publicly paper and electronic copies of this thesis document in whole or in part. Signature of author_________________________________________________ Department of Linguistics and Philosophy August 25, 2000 Certified by_______________________________________________________ Professor Michael Kenstowicz Thesis supervisor Accepted by______________________________________________________ Alec Marantz Chairman, Department of Linguistics and Philosophy CONSONANT CLUSTER PHONOTACTICS: A PERCEPTUAL APPROACH NOTES ON THE PRESENT VERSION by The present version, finished in July 2001, differs slightly from the official one, deposited in September 2000. The acknowledgments were finally added. The MARIE-HÉLÈNE CÔTÉ formatting was changed and the presentation generally improved. Several typos were corrected, and the references were updated, when papers originally cited as manuscripts were subsequently published. A couple of references were also added, as Submitted to the Department of Linguistics and Philosophy well as short conclusions to chapters 3, 4, and 5, which for the most part summarize on September 5, 2000, in partial fulfillment of the requirements the chapter in question. -

On Syncope in Old English
In: Dieter Kastovsky and Aleksander Szwedek (eds) Linguistics across historical and geographical boundaries. In honour of Jacek Fisiak on the occasion of his fiftieth birthday. Berlin: Mouton-de Gruyter, 1986, 359-66. On syncope in Old English Raymond Hickey University of Bonn Abstract. Syncope in Old English is seen to be a rule which is determined by syllable structure but furthermore to be governed by a set of restricting conditions which refer to the world-class status of the forms which may act as input to the syncope rule, and also to the inflectional or derivational nature of the suffix which are added also to the precise phonological structure of those forms which undergo syncope. A phonological rule in a language which does not operate globally is always of particular interest as the conditions which restrict its application can frequently be recognized and formulized, at the same time throwing light on the nature of conditions which can in principle apply in a language’s phonology. In Old English a syncope rule existed which clearly related to the syllable structure of the forms it did not operate on but which was also subject to a set of restricting conditions which lie outside the domain of the syllable. The examination of this syncope rule and the conditions pertaining to it is the subject of this contribution. It is first of all necessary to distinguish syncope from another phonological process with which it might be confused. This is epenthesis, which appears to have been quite widespread in late West Saxon, as can be seen in the following forms. -
![Arxiv:0809.1487V2 [Cond-Mat.Stat-Mech] 25 Oct 2008 the first Two Authors Acknowledge Equal Contributions to This Review](https://docslib.b-cdn.net/cover/5965/arxiv-0809-1487v2-cond-mat-stat-mech-25-oct-2008-the-rst-two-authors-acknowledge-equal-contributions-to-this-review-695965.webp)
Arxiv:0809.1487V2 [Cond-Mat.Stat-Mech] 25 Oct 2008 the first Two Authors Acknowledge Equal Contributions to This Review
Advances in Physics Vol. 00, No. 00, Month-Month 200x, 1–111 Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques P. B. Blakiea∗, A. S. Bradleya;b, M. J. Davisb, R. J. Ballagha, and C. W. Gardinera aJack Dodd Centre for Quantum Technology, Department of Physics, University of Otago, Dunedin, New Zealand; bThe University of Queensland, School of Physical Sciences, ARC Centre of Excellence for Quantum-Atom Optics, Qld 4072, Australia (Received 00 Month 200x; In final form 00 Month 200x) We review phase space techniques based on the Wigner representation that provide an approximate description of dilute ultra-cold Bose gases. In this approach the quantum field evolution can be represented using equations of motion of a similar form to the Gross-Pitaevskii equation but with stochastic modifications that include quantum effects in a controlled degree of approximation. These techniques provide a practical quantitative description of both equilibrium and dynamical properties of Bose gas systems. We develop versions of the formalism appropriate at zero temperature, where quantum fluctuations can be important, and at finite temperature where thermal fluctuations dominate. The numerical techniques necessary for implementing the formalism are discussed in detail, together with methods for extracting observables of interest. Numerous applications to a wide range of phenomena are presented. Keywords: Ultra-cold Bose gas, quantum and finite temperature dynamics. ∗Corresponding author. Email: [email protected] arXiv:0809.1487v2 [cond-mat.stat-mech] 25 Oct 2008 The first two authors acknowledge equal contributions to this review. 2 Contents 1. Introduction 4 2. Background formalism 7 2.1. -

Phonotactics on the Web 487
PHONOTACTICS ON THE WEB 487 APPENDIX Table A1 International Phonetic Alphabet (IPA) and Computer-Readable “Klattese” Transcription Equivalents IPAKlattese IPA Klattese Stops Syllabic Consonants p p n N t t m M k k l L b b d d Glides and Semivowels g l l ɹ r Affricates w w tʃ C j y d J Vowels Sibilant Fricatives i i s s I ʃ S ε E z z e e Z @ Nonsibilant Fricatives ɑ a ɑu f f W θ a Y T v v ^ ð ɔ c D o h h O o o Nasals υ U n n u u m m R ŋ G ə x | X Klattese Transcription Conventions Repeated phonemes. The only situation in which a phoneme is repeated is in a compound word. For exam- ple, the word homemade is transcribed in Klattese as /hommed/. All other words with two successive phonemes that are the same just have a single segment. For example, shrilly would be transcribed in Klattese as /SrIli/. X/R alternation. /X/ appears only in unstressed syllables, and /R/ appears only in stressed syllables. Schwas. There are four schwas: /x/, /|/, /X/, and unstressed /U/. The /U/ in an unstressed syllable is taken as a rounded schwa. Syllabic consonants. The transcriptions are fairly liberal in the use of syllabic consonants. Words ending in -ism are transcribed /IzM/ even though a tiny schwa typically appears in the transition from the /z/ to the /M/. How- ever, /N/ does not appear unless it immediately follows a coronal. In general, /xl/ becomes /L/ unless it occurs be- fore a stressed vowel. -
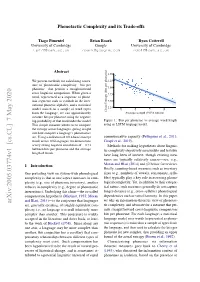
Phonotactic Complexity and Its Trade-Offs
Phonotactic Complexity and its Trade-offs Tiago Pimentel Brian Roark Ryan Cotterell University of Cambridge Google University of Cambridge [email protected] [email protected] [email protected] Abstract 3.50 We present methods for calculating a mea- 3.25 sure of phonotactic complexity—bits per phoneme—that permits a straightforward 3.00 cross-linguistic comparison. When given a 2.75 word, represented as a sequence of phone- mic segments such as symbols in the inter- 2.50 national phonetic alphabet, and a statistical 2.25 model trained on a sample of word types 5 6 7 8 from the language, we can approximately Cross Entropy (bits per phoneme) Average Length (# IPA tokens) measure bits per phoneme using the negative log-probability of that word under the model. Figure 1: Bits-per-phoneme vs average word length This simple measure allows us to compare using an LSTM language model. the entropy across languages, giving insight into how complex a language’s phonotactics are. Using a collection of 1016 basic concept communicative capacity (Pellegrino et al., 2011; words across 106 languages, we demonstrate Coupé et al., 2019). a very strong negative correlation of −0:74 Methods for making hypotheses about linguis- between bits per phoneme and the average tic complexity objectively measurable and testable length of words. have long been of interest, though existing mea- sures are typically relatively coarse—see, e.g., 1 Introduction Moran and Blasi(2014) and §2 below for reviews. Briefly, counting-based measures such as inventory One prevailing view on system-wide phonological sizes (e.g., numbers of vowels, consonants, sylla- complexity is that as one aspect increases in com- bles) typically play a key role in assessing phono- plexity (e.g., size of phonemic inventory), another logical complexity. -

Quantum Markov Chain Mixing and Dissipative Engineering
Quantum Markov Chain Mixing and Dissipative Engineering Kastoryano, Michael James Publication date: 2012 Document version Early version, also known as pre-print Citation for published version (APA): Kastoryano, M. J. (2012). Quantum Markov Chain Mixing and Dissipative Engineering. Download date: 27. Sep. 2021 FACULTY OF SCIENCE UNIVERSITY OF COPENHAGEN Quantum Markov Chain Mixing and Dissipative Engineering PhD thesis Michael James Kastoryano The PhD School of Science Quantum Information Group QUANTOP – Danish National Research Foundation Centre for Quantum Optics Niels Bohr Institute and Niels Bohr International Academy Academic supervisors: Michael M. Wolf and Anders S. Sørensen December, 2011 Quantum Markov Chain Mixing and Dissipative Engineering Michael James Kastoryano This thesis is submitted in partial fulfilment of the requirements for the Ph.D. degree at the University of Copenhagen. Copyright c 2011 Michael James Kastoryano Abstract This thesis is the fruit of investigations on the extension of ideas of Markov chain mixing to the quantum setting, and its application to problems of dissipative engineering. A Markov chain describes a statistical process where the probability of future events depends only on the state of the system at the present point in time, but not on the history of events. Very many important processes in nature are of this type, therefore a good understanding of their behavior has turned out to be very fruitful for science. Markov chains always have a non-empty set of limiting distributions (stationary states). The aim of Markov chain mixing is to obtain (upper and/or lower) bounds on the number of steps it takes for the Markov chain to reach a stationary state. -

Alternatives to the Syllabic Interpretation Of
ALTERNATIVES TO SYLLABLE-BASED ACCOUNTS OF CONSONANTAL PHONOTACTICS Donca Steriade, UCLA Abstract Phonotactic statements characterize contextual restrictions on the occurrence of segments or feature values. This study argues that consonantal phonotactics are best understood as syllable-independent, string-based conditions reflecting positional differences in the perceptibility of contrasts. The analyses proposed here have better empirical coverage compared to syllable-based analyses that link a consonant's feature realization to its syllabic position. Syllable-based analyses require identification of word-medial syllabic divisions; the account proposed here does not and this may be a significant advantage. Word-medial syllable- edges are, under specific conditions, not uniformly identified by speakers; but comparable variability does not exist for phonotactic knowledge. The paper suggests that syllable- independent conditions define segmental phonotactics, and that word-edge phonotactics, in turn, are among the guidelines used by speakers to infer word-internal syllable divisions. 1. Introduction. The issue addressed here is the link between consonantal phonotactics and syllable structure conditions. Consider a paradigm case of the role attributed to syllables in current accounts of consonant distributions, based on Kahn (1976). Kahn suggests a syllable- based explanation of the fact that tpt, dbd, tkt, dgd strings - two coronal stops surrounding a non-coronal - are impossible in English. Kahn explains this gap by combining three hypotheses, two of which are specific to English, and a third with potential as a universal: (i) English onsets cannot contain stop-stop sequences; (ii) alveolar stops cannot precede non-coronals in English codas; and (iii) each segment/feature must belong to some syllable. -

1 Phonotactics As Phonology: Knowledge of a Complex Constraint in Dutch René Kager (Utrecht University) and Joe Pater (Universi
Phonotactics as phonology: Knowledge of a complex constraint in Dutch René Kager (Utrecht University) and Joe Pater (University of Massachusetts, Amherst) Abstract : The Dutch lexicon contains very few sequences of a long vowel followed by a consonant cluster, where the second member of the cluster is a non-coronal. We provide experimental evidence that Dutch speakers have implicit knowledge of this gap, which cannot be reduced to the probability of segmental sequences or to word-likeness as measured by neighborhood density. The experiment also shows that the ill-formedness of this sequence is mediated by syllable structure: it has a weaker effect on judgments when the last consonant begins a new syllable. We provide an account in terms of Hayes and Wilson’s Maximum Entropy model of phonotactics, using constraints that go beyond the complexity permitted by their model of constraint induction. 1. Introduction Phonological analysis and theorizing typically takes phonotactics as part of the data to be accounted for in terms of a phonological grammar. Ohala (1986) challenges this assumption, raising the possibility that knowledge of the shape of a language’s words could be reduced to “knowledge of the lexicon plus the possession of very general cognitive abilities”. 1 As an example of the requisite general cognitive abilities, he points to Greenberg and Jenkins’ (1964) similarity metric, which measures the closeness of a nonce word to the existing lexicon as proportional to the number of real words obtained by substituting any set of the nonce word’s segments with other segments. Like many other models of word-likeness or probability, Greenberg and Jenkins’ model of phonotactic knowledge is quite different from those constructed in phonological theory. -

Exact Calculation of Entanglement in a 19-Site 2D Spin System
Exact Calculation of Entanglement in a 19-site 2D Spin System Qing Xu,1 Sabre Kais∗,2 Maxim Naumov,3 and Ahmed Sameh3 1Department of Physics, Purdue University, West Lafayette, Indiana 47907, USA 2Department of Chemistry and Birck Nanotechnology center, Purdue University, West Lafayette, Indiana 47907, USA 3Department of Computer Science, Purdue University, West Lafayette, Indiana 47907, USA (Dated: October 22, 2018) Using the Trace Minimization Algorithm, we carried out an exact calculation of entanglement in 1 a 19-site two-dimensional transverse Ising model. This model consists of a set of localized spin- 2 particles in a two dimensional triangular lattice coupled through exchange interaction J and subject to an external magnetic field of strength h. We demonstrate, for such a class of two-dimensional magnetic systems, that entanglement can be controlled and tuned by varying the parameter λ = h/J in the Hamiltonian and by introducing impurities into the systems. Examining the derivative of the concurrence as a function of λ shows that the system exhibits a quantum phase transition at about λc = 3.01, a transition induced by quantum fluctuations at the absolute zero of temperature. PACS numbers: 03.67.Mn I. INTRODUCTION Entanglement, which is a quantum mechanical property that has no classical analog, has been viewed as a resource of quantum information and computation [1–8]. Intensive researches of entanglement measurement, entanglement monotone, criteria for distinguishing separable from entangled pure states and all the extensions from bipartite to multipartite systems have been carried out both qualitatively and quantitatively [1]. At the interface between quantum information and statistical mechanics, there has been particular analysis of entanglement in quantum critical models [9–12]. -

Chapter on Phonology
13 The (American) English Sound System 13.1a IPA Chart Consonants: Place & Manner of Articulation bilabial labiodental interdental alveolar palatal velar / glottal Plosives: [+voiced] b d g [voiced] p t k Fricatives: [+voiced] v ð z ž [voiced] f θ s š h Affricates: [+voiced] ǰ [voiced] č *Nasals: [+voiced] m n ŋ *Liquids: l r *Glides: w y *Syllabic Nasals and Liquids. When nasals /m/, /n/ and liquids /l/, /r/ take on vowellike properties, they are said to become syllabic: e.g., /ļ/ and /ŗ/ (denoted by a small line diacritic underneath the grapheme). Note how token examples (teacher) /tičŗ/, (little) /lIt ļ/, (table) /tebļ/ (vision) /vIžņ/, despite their creating syllable structures [CVCC] ([CVCC] = consonantvowel consonantconsonant), nonetheless generate a bisyllabic [CVCV] structure whereby we can ‘clapout’ by hand two syllables—e.g., [ [/ ti /] [/ čŗ /] ] and 312 Chapter Thirteen [ [/ lI /] [/ tļ /] ], each showing a [CVCC v] with final consonant [C v] denoting a vocalic /ŗ/ and /ļ/ (respectively). For this reason, ‘fluid’ [Consonantal] (vowellike) nasals, liquids (as well as glides) fall at the bottom half of the IPA chart in opposition to [+Consonantal] stops. 13.1b IPA American Vowels Diphthongs front: back: high: i u ay I ә U oy au e ^ o ε * ] low: æ a 13.1c Examples of IPA: Consonants / b / ball, rob, rabbit / d / dig, sad, sudden / g / got, jogger / p / pan, tip, rapper / t / tip, fit, punter / k / can, keep / v / vase, love / z / zip, buzz, cars / ž / measure, pleasure / f / fun, leaf / s / sip, cent, books / š / shoe, ocean, pressure / ð / the, further / l / lip, table, dollar / č / chair, cello / θ / with, theory / r / red, fear / ǰ / joke, lodge / w / with, water / y / you, year / h / house / m / make, ham / n / near, fan / ŋ / sing, pink The American English Sound System 313 *Note: Many varieties of American English cannot distinguish between the ‘open‘O’ vowel /]/ e.g., as is sounded in caught /k]t/ vs. -

Vowel Epenthesis, Acoustics and Phonology Patterns in Moroccan Arabic Azra Ali, Mohamed Lahrouchi, Michael Ingleby
Vowel Epenthesis, Acoustics and Phonology Patterns in Moroccan Arabic Azra Ali, Mohamed Lahrouchi, Michael Ingleby To cite this version: Azra Ali, Mohamed Lahrouchi, Michael Ingleby. Vowel Epenthesis, Acoustics and Phonology Patterns in Moroccan Arabic. Interspeech 2008, 2008, Brisbane, Australia. pp.1178-1181. halshs-00432598 HAL Id: halshs-00432598 https://halshs.archives-ouvertes.fr/halshs-00432598 Submitted on 16 Nov 2009 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Vowel Epenthesis, Acoustics and Phonology Patterns in Moroccan Arabic Azra N. Ali 1, Mohamed Lahrouchi 2, Michael Ingleby 1 1 School of Computing and Engineering, University of Huddersfield, Huddersfield, England. 2 CNRS, Paris-8, Paris, France. [email protected], [email protected], [email protected] The most interesting early findings were made by Abstract Baothman et al. [5,6], who confirmed empirically in a large In Moroccan Arabic it is widely accepted that short vowels corpus of spoken Saudi Arabic that it has no branching are mostly elided, resulting in consonant clusters and onsets. She also found evidence in recordings and consonant geminates. In this paper we present evidence from spectrograms that a phonologically active sukuun is present our exploratory timing study that challenges this widely between clusters.