Graph Theory and Additive Combinatorics, a Graduate-Level Course Taught by Prof
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pseudorandom Ramsey Graphs
Pseudorandom Ramsey Graphs Jacques Verstraete, UCSD [email protected] Abstract We outline background to a recent theorem [47] connecting optimal pseu- dorandom graphs to the classical off-diagonal Ramsey numbers r(s; t) and graph Ramsey numbers r(F; t). A selection of exercises is provided. Contents 1 Linear Algebra 1 1.1 (n; d; λ)-graphs . 2 1.2 Alon-Boppana Theorem . 2 1.3 Expander Mixing Lemma . 2 2 Extremal (n; d; λ)-graphs 3 2.1 Triangle-free (n; d; λ)-graphs . 3 2.2 Clique-free (n; d; λ)-graphs . 3 2.3 Quadrilateral-free graphs . 4 3 Pseudorandom Ramsey graphs 4 3.1 Independent sets . 4 3.2 Counting independent sets . 5 3.3 Main Theorem . 5 4 Constructing Ramsey graphs 5 4.1 Subdivisions and random blocks . 6 4.2 Explicit Off-Diagonal Ramsey graphs . 7 5 Multicolor Ramsey 7 5.1 Blowups . 8 1. Linear Algebra X. Since trace is independent of basis, for k ≥ 1: n If A is a square symmetric matrix, then the eigenvalues X tr(Ak) = tr(X−kAkXk) = tr(Λk) = λk: (2) of A are real. When A is an n by n matrix, we denote i i=1 them λ1 ≥ λ2 ≥ · · · ≥ λn. If the corresponding eigen- k vectors forming an orthonormal basis are e1; e2; : : : ; en, The combinatorial interpretation of tr(A ) as the num- n P then for any x 2 R , we may write x = xiei and ber of closed walks of length k in the graph G will be used frequently. When A is the adjacency matrix of a n n X 2 X graph G, we write λi(G) for the ith largest eigenvalue hAx; xi = λixi and hAx; yi = λixiyi: (1) i=1 i=1 of A and For any i 2 [n], note xi = hx; eii. -
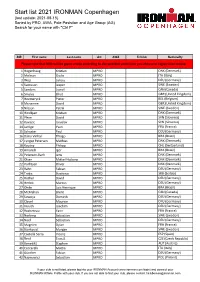
Start List 2021 IRONMAN Copenhagen (Last Update: 2021-08-15) Sorted by PRO, AWA, Pole Posistion and Age Group (AG) Search for Your Name with "Ctrl F"
Start list 2021 IRONMAN Copenhagen (last update: 2021-08-15) Sorted by PRO, AWA, Pole Posistion and Age Group (AG) Search for your name with "Ctrl F" BIB First name Last name AG AWA TriClub Nationallty Please note that BIBs will be given onsite according to the selected swim time you choose in registration oniste. 1 Hogenhaug Kristian MPRO DNK (Denmark) 2 Molinari Giulio MPRO ITA (Italy) 3 Wojt Lukasz MPRO DEU (Germany) 4 Svensson Jesper MPRO SWE (Sweden) 5 Sanders Lionel MPRO CAN (Canada) 6 Smales Elliot MPRO GBR (United Kingdom) 7 Heemeryck Pieter MPRO BEL (Belgium) 8 Mcnamee David MPRO GBR (United Kingdom) 9 Nilsson Patrik MPRO SWE (Sweden) 10 Hindkjær Kristian MPRO DNK (Denmark) 11 Plese David MPRO SVN (Slovenia) 12 Kovacic Jaroslav MPRO SVN (Slovenia) 14 Jarrige Yvan MPRO FRA (France) 15 Schuster Paul MPRO DEU (Germany) 16 Dário Vinhal Thiago MPRO BRA (Brazil) 17 Lyngsø Petersen Mathias MPRO DNK (Denmark) 18 Koutny Philipp MPRO CHE (Switzerland) 19 Amorelli Igor MPRO BRA (Brazil) 20 Petersen-Bach Jens MPRO DNK (Denmark) 21 Olsen Mikkel Hojborg MPRO DNK (Denmark) 22 Korfitsen Oliver MPRO DNK (Denmark) 23 Rahn Fabian MPRO DEU (Germany) 24 Trakic Strahinja MPRO SRB (Serbia) 25 Rother David MPRO DEU (Germany) 26 Herbst Marcus MPRO DEU (Germany) 27 Ohde Luis Henrique MPRO BRA (Brazil) 28 McMahon Brent MPRO CAN (Canada) 29 Sowieja Dominik MPRO DEU (Germany) 30 Clavel Maurice MPRO DEU (Germany) 31 Krauth Joachim MPRO DEU (Germany) 32 Rocheteau Yann MPRO FRA (France) 33 Norberg Sebastian MPRO SWE (Sweden) 34 Neef Sebastian MPRO DEU (Germany) 35 Magnien Dylan MPRO FRA (France) 36 Björkqvist Morgan MPRO SWE (Sweden) 37 Castellà Serra Vicenç MPRO ESP (Spain) 38 Řenč Tomáš MPRO CZE (Czech Republic) 39 Benedikt Stephen MPRO AUT (Austria) 40 Ceccarelli Mattia MPRO ITA (Italy) 41 Günther Fabian MPRO DEU (Germany) 42 Najmowicz Sebastian MPRO POL (Poland) If your club is not listed, please log into your IRONMAN Account (www.ironman.com/login) and connect your IRONMAN Athlete Profile with your club. -

Legacy Image
5-(948-~gblb SOWARE ENGINEERING LABORATORY SERIES SEL-95-004 PROCEEDINGS OF THE TWENTIETH ANNUAL SOFTWARE ENGINEERING WORKSHOP DECEMBER 1995 National Aeronautics and Space Administration Goddard Space Flight Center Greenbelt, Maryland 20771 Proceedings of the Twentieth Annual Software Engineering Workshop November 29-30,1995 GODDARD SPACE FLIGHT CENTER Greenbelt, Maryland The Software Engineering Laboratory (SEL) is an organization sponsored by the National Aeronautics and Space AdministratiodGoddard Space Flight Center (NASAIGSFC) and created to investigate the effectiveness of software engineering technologies when applied to the development of applications software. The SEL was created in 1976 and has three primary organizational members: NASAIGSFC, Software Engineering Branch The University of Maryland, Department of Computer Science .I Computer Sciences Corporation, Software Engineering Operation The goals of the SEL are (1) to understand the software development process in the GSFC environment; (2) to measure the effects of various methodologies, tools, and models on this process; and (3) to identifjr and then to apply successful development practices. The activities, findings, and recommendations of the SEL are recorded in the Software Engineering Laboratory Series, a continuing series of reports that includes this document. Documents from the Software Engineering Laboratory Series can be obtained via the SEL homepage at: or by writing to: Software Engineering Branch Code 552 Goddard Space Flight Center Greenbelt, Maryland 2077 1 SEW Proceedings iii The views and findings expressed herein are those of, the authors and presenters and do not necessarily represent the views, estimates, or policies of the SEL. All material herein is reprinted as submitted by authors and presenters, who are solely responsible for compliance with any relevant copyright, patent, or other proprietary restrictions. -

Forbidding Subgraphs
Graph Theory and Additive Combinatorics Lecturer: Prof. Yufei Zhao 2 Forbidding subgraphs 2.1 Mantel’s theorem: forbidding a triangle We begin our discussion of extremal graph theory with the following basic question. Question 2.1. What is the maximum number of edges in an n-vertex graph that does not contain a triangle? Bipartite graphs are always triangle-free. A complete bipartite graph, where the vertex set is split equally into two parts (or differing by one vertex, in case n is odd), has n2/4 edges. Mantel’s theorem states that we cannot obtain a better bound: Theorem 2.2 (Mantel). Every triangle-free graph on n vertices has at W. Mantel, "Problem 28 (Solution by H. most bn2/4c edges. Gouwentak, W. Mantel, J. Teixeira de Mattes, F. Schuh and W. A. Wythoff). Wiskundige Opgaven 10, 60 —61, 1907. We will give two proofs of Theorem 2.2. Proof 1. G = (V E) n m Let , a triangle-free graph with vertices and x edges. Observe that for distinct x, y 2 V such that xy 2 E, x and y N(x) must not share neighbors by triangle-freeness. Therefore, d(x) + d(y) ≤ n, which implies that d(x)2 = (d(x) + d(y)) ≤ mn. ∑ ∑ N(y) x2V xy2E y On the other hand, by the handshake lemma, ∑x2V d(x) = 2m. Now by the Cauchy–Schwarz inequality and the equation above, Adjacent vertices have disjoint neigh- borhoods in a triangle-free graph. !2 ! 4m2 = ∑ d(x) ≤ n ∑ d(x)2 ≤ mn2; x2V x2V hence m ≤ n2/4. -

The History of Degenerate (Bipartite) Extremal Graph Problems
The history of degenerate (bipartite) extremal graph problems Zolt´an F¨uredi and Mikl´os Simonovits May 15, 2013 Alfr´ed R´enyi Institute of Mathematics, Budapest, Hungary [email protected] and [email protected] Abstract This paper is a survey on Extremal Graph Theory, primarily fo- cusing on the case when one of the excluded graphs is bipartite. On one hand we give an introduction to this field and also describe many important results, methods, problems, and constructions. 1 Contents 1 Introduction 4 1.1 Some central theorems of the field . 5 1.2 Thestructureofthispaper . 6 1.3 Extremalproblems ........................ 8 1.4 Other types of extremal graph problems . 10 1.5 Historicalremarks . .. .. .. .. .. .. 11 arXiv:1306.5167v2 [math.CO] 29 Jun 2013 2 The general theory, classification 12 2.1 The importance of the Degenerate Case . 14 2.2 The asymmetric case of Excluded Bipartite graphs . 15 2.3 Reductions:Hostgraphs. 16 2.4 Excluding complete bipartite graphs . 17 2.5 Probabilistic lower bound . 18 1 Research supported in part by the Hungarian National Science Foundation OTKA 104343, and by the European Research Council Advanced Investigators Grant 267195 (ZF) and by the Hungarian National Science Foundation OTKA 101536, and by the European Research Council Advanced Investigators Grant 321104. (MS). 1 F¨uredi-Simonovits: Degenerate (bipartite) extremal graph problems 2 2.6 Classification of extremal problems . 21 2.7 General conjectures on bipartite graphs . 23 3 Excluding complete bipartite graphs 24 3.1 Bipartite C4-free graphs and the Zarankiewicz problem . 24 3.2 Finite Geometries and the C4-freegraphs . -

Discrete Mathematics Lecture Notes Incomplete Preliminary Version
Discrete Mathematics Lecture Notes Incomplete Preliminary Version Instructor: L´aszl´oBabai Last revision: June 22, 2003 Last update: April 2, 2021 Copyright c 2003, 2021 by L´aszl´oBabai All rights reserved. Contents 1 Logic 1 1.1 Quantifier notation . 1 1.2 Problems . 1 2 Asymptotic Notation 5 2.1 Limit of sequence . 6 2.2 Asymptotic Equality and Inequality . 6 2.3 Little-oh notation . 9 2.4 Big-Oh, Omega, Theta notation (O, Ω, Θ) . 9 2.5 Prime Numbers . 11 2.6 Partitions . 11 2.7 Problems . 12 3 Convex Functions and Jensen's Inequality 15 4 Basic Number Theory 19 4.1 Introductory Problems: g.c.d., congruences, multiplicative inverse, Chinese Re- mainder Theorem, Fermat's Little Theorem . 19 4.2 Gcd, congruences . 24 4.3 Arithmetic Functions . 26 4.4 Prime Numbers . 30 4.5 Quadratic Residues . 33 4.6 Lattices and diophantine approximation . 34 iii iv CONTENTS 5 Counting 37 5.1 Binomial coefficients . 37 5.2 Recurrences, generating functions . 40 6 Graphs and Digraphs 43 6.1 Graph Theory Terminology . 43 6.1.1 Planarity . 52 6.1.2 Ramsey Theory . 56 6.2 Digraph Terminology . 57 6.2.1 Paradoxical tournaments, quadratic residues . 61 7 Finite Probability Spaces 63 7.1 Finite probability space, events . 63 7.2 Conditional probability, probability of causes . 65 7.3 Independence, positive and negative correlation of a pair of events . 67 7.4 Independence of multiple events . 68 7.5 Random graphs: The Erd}os{R´enyi model . 71 7.6 Asymptotic evaluation of sequences . -

Octonion Multiplication and Heawood's
CONFLUENTES MATHEMATICI Bruno SÉVENNEC Octonion multiplication and Heawood’s map Tome 5, no 2 (2013), p. 71-76. <http://cml.cedram.org/item?id=CML_2013__5_2_71_0> © Les auteurs et Confluentes Mathematici, 2013. Tous droits réservés. L’accès aux articles de la revue « Confluentes Mathematici » (http://cml.cedram.org/), implique l’accord avec les condi- tions générales d’utilisation (http://cml.cedram.org/legal/). Toute reproduction en tout ou partie de cet article sous quelque forme que ce soit pour tout usage autre que l’utilisation á fin strictement personnelle du copiste est constitutive d’une infrac- tion pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. cedram Article mis en ligne dans le cadre du Centre de diffusion des revues académiques de mathématiques http://www.cedram.org/ Confluentes Math. 5, 2 (2013) 71-76 OCTONION MULTIPLICATION AND HEAWOOD’S MAP BRUNO SÉVENNEC Abstract. In this note, the octonion multiplication table is recovered from a regular tesse- lation of the equilateral two timensional torus by seven hexagons, also known as Heawood’s map. Almost any article or book dealing with Cayley-Graves algebra O of octonions (to be recalled shortly) has a picture like the following Figure 0.1 representing the so-called ‘Fano plane’, which will be denoted by Π, together with some cyclic ordering on each of its ‘lines’. The Fano plane is a set of seven points, in which seven three-point subsets called ‘lines’ are specified, such that any two points are contained in a unique line, and any two lines intersect in a unique point, giving a so-called (combinatorial) projective plane [8,7]. -

Pseudorandom Graphs
Pseudorandom graphs David Conlon What is a pseudorandom graph? A pseudorandom graph is a graph that behaves like a random graph of the same edge density. For example, it might be the case that the graph has roughly the same edge density between any two large sets or that it contains roughly the same number of copies of every small graph H as one would expect to find in a random graph. The purpose of this course will be to explore certain notions of pseudorandomness and to see what properties the resulting graphs have. For much of the course, our basic object of study will be (p; β)-jumbled graphs, a concept introduced (in a very slightly different form) by Andrew Thomason in the 1980s. These are defined as follows. Definition 1 A graph G on vertex set V is (p; β)-jumbled if, for all vertex subsets X; Y ⊆ V (G), je(X; Y ) − pjXjjY jj ≤ βpjXjjY j: That is, the edge density between any two sets X and Y is roughly p, with the allowed discrepancy measured in terms of β. The normalisation may be explained by considering what happens in a random graph. In this case, the expected number of edges between X and Y will be pjXjjY j and the standard deviation will be pp(1 − p)jXjjY j. So β is measuring how many multiples of the standard deviation our edge density is allowed to deviate by. Of course, random graphs should themselves be pseudorandom. Recall that the binomial random graph G(n; p) is a graph on n vertices formed by choosing each edge independently with probability p. -

Dirichlet Character Difference Graphs 1
DIRICHLET CHARACTER DIFFERENCE GRAPHS M. BUDDEN, N. CALKINS, W. N. HACK, J. LAMBERT and K. THOMPSON Abstract. We define Dirichlet character difference graphs and describe their basic properties, includ- ing the enumeration of triangles. In the case where the modulus is an odd prime, we exploit the spectral properties of such graphs in order to provide meaningful upper bounds for their diameter. 1. Introduction Upon one's first encounter with abstract algebra, a theorem which resonates throughout the theory is Cayley's theorem, which states that every finite group is isomorphic to a subgroup of some symmetric group. The significance of such a result comes from giving all finite groups a common ground by allowing one to focus on groups of permutations. It comes as no surprise that algebraic graph theorists chose the name Cayley graphs to describe graphs which depict groups. More formally, if G is a group and S is a subset of G closed under taking inverses and not containing the identity, then the Cayley graph, Cay(G; S), is defined to be the graph with vertex set G and an edge occurring between the vertices g and h if hg−1 2 S [9]. Some of the first examples of JJ J I II Cayley graphs that are usually encountered include the class of circulant graphs. A circulant graph, denoted by Circ(m; S), uses Z=mZ as the group for a Cayley graph and the generating set S is Go back m chosen amongst the integers in the set f1; 2; · · · b 2 cg [2]. -

The Regularity Method for Graphs with Few 4-Cycles
THE REGULARITY METHOD FOR GRAPHS WITH FEW 4-CYCLES DAVID CONLON, JACOB FOX, BENNY SUDAKOV, AND YUFEI ZHAO Abstract. We develop a sparse graph regularity method that applies to graphs with few 4-cycles, including new counting and removal lemmas for 5-cycles in such graphs. Some applications include: • Every n-vertex graph with no 5-cycle can be made triangle-free by deleting o(n3=2) edges. • For r ≥ 3, every n-vertex r-graph with girth greater than 5 has o(n3=2) edges. • Every subset of [n] without a nontrivial solution to the equation x + x + 2x = x + 3x has p 1 2 3 4 5 size o( n). 1. Introduction Szemerédi’s regularity lemma [52] is a rough structure theorem that applies to all graphs. The lemma originated in Szemerédi’s proof of his celebrated theorem that dense sets of integers contain arbitrarily long arithmetic progressions [51] and is now considered one of the most useful and important results in combinatorics. Among its many applications, one of the earliest was the influential triangle removal lemma of Ruzsa and Szemerédi [40], which says that any n-vertex graph with o(n3) triangles can be made triangle-free by removing o(n2) edges. Surprisingly, this simple sounding statement is already sufficient to imply Roth’s theorem, the special case of Szemerédi’s theorem for 3-term arithmetic progressions, and a generalization known as the corners theorem. Most applications of the regularity lemma, including the triangle removal lemma, rely on also having an associated counting lemma. Such a lemma roughly says that the number of embeddings of a fixed graph H into a pseudorandom graph G can be estimated by pretending that G is a random graph. -

Introducing the Mini-DML Project Thierry Bouche
Introducing the mini-DML project Thierry Bouche To cite this version: Thierry Bouche. Introducing the mini-DML project. ECM4 Satellite Conference EMANI/DML, Jun 2004, Stockholm, Sweden. 11 p.; ISBN 3-88127-107-4. hal-00347692 HAL Id: hal-00347692 https://hal.archives-ouvertes.fr/hal-00347692 Submitted on 16 Dec 2008 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Introducing the mini-DML project Thierry Bouche Université Joseph Fourier (Grenoble) WDML workshop Stockholm June 27th 2004 Introduction At the Göttingen meeting of the Digital mathematical library project (DML), in May 2004, the issue was raised that discovery and seamless access to the available digitised litterature was still a task to be acomplished. The ambitious project of a comprehen- sive registry of all ongoing digitisation activities in the field of mathematical research litterature was agreed upon, as well as the further investigation of many linking op- tions to ease user’s life. However, given the scope of those projects, their benefits can’t be expected too soon. Between the hope of a comprehensive DML with many eYcient entry points and the actual dissemination of heterogeneous partial lists of available material, there is a path towards multiple distributed databases allowing integrated search, metadata exchange and powerful interlinking. -

Graph Theory
Graph theory Eric Shen Friday, August 28, 2020 The contents of this handout are based on various lectures on graph theory I have heard over the years, including some from MOP and some from Canada/USA Mathcamp. Contents 1. Basic terminology3 1.1. Introduction to graphs ................................ 3 1.2. Dictionary ....................................... 3 2. Basic graph facts4 2.1. Trees .......................................... 4 2.2. Handshaking lemma.................................. 5 2.3. Example problems................................... 5 3. Colorings of graphs7 3.1. Introduction to coloring................................ 7 3.2. Planar graphs ..................................... 7 3.3. Four-color theorem .................................. 8 3.4. Example problems................................... 8 4. Combinatorial constructions 10 4.1. Basic graph constructions............................... 10 4.2. Perfect matchings................................... 11 4.3. Corollaries of Hall's theorem............................. 11 4.4. A hard walkthrough.................................. 12 5. Extremal graph theory 13 5.1. Triangle-free bounds.................................. 13 5.2. Formalization ..................................... 14 5.3. Tur´angraphs...................................... 14 5.4. Example problems................................... 15 6. Application: crossing numbers 17 6.1. Conventional definitions................................ 17 6.2. Some conjectures ................................... 17 6.3. Crossing number