DOCSLIB.ORG

Weighted-SAMGSR: Combining Significance Analysis of Microarray

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Weighted-SAMGSR: Combining Significance Analysis of Microarray Tian et al. Biology Direct (2016) 11:50 DOI 10.1186/s13062-016-0152-3 RESEARCH Open Access Weighted-SAMGSR: combining significance analysis of microarray-gene set reduction algorithm with pathway topology-based weights to select relevant genes Suyan Tian1,2*, Howard H. Chang3 and Chi Wang4 Abstract Background: It has been demonstrated that a pathway-based feature selection method that incorporates biological information within pathways during the process of feature selection usually outperforms a gene-based feature selection algorithm in terms of predictive accuracy and stability. Significance analysis of microarray-gene set reduction algorithm (SAMGSR), an extension to a gene set analysis method with further reduction of the selected pathways to their respective core subsets, can be regarded as a pathway-based feature selection method. Methods: In SAMGSR, whether a gene is selected is mainly determined by its expression difference between the phenotypes, and partially by the number of pathways to which this gene belongs. It ignores the topology information among pathways. In this study, we propose a weighted version of the SAMGSR algorithm by constructing weights based on the connectivity among genes and then combing these weights with the test statistics. Results: Using both simulated and real-world data, we evaluate the performance of the proposed SAMGSR extension and demonstrate that the weighted version outperforms its original version. Conclusions: To conclude, the additional gene connectivity information does faciliatate feature selection. Reviewers: This article was reviewed by Drs. Limsoon Wong, Lev Klebanov, and, I. King Jordan. Keywords: Pathway knowledge, Pathway-based feature selection, Significance analysis of microarray (SAM), Weighted gene expression profiles, Non-small cell lung cancer (NSCLC), Multiple sclerosis (MS) Background In contrast to a pathway analysis method, which Many studies have demonstrated that pathway-based examines the association of a whole pathway with the feature selection algorithms, which utilize biological phenotype of interest, a pathway-based feature selection information contained in pathways to guide which algorithm focuses on the identification of relevant features/genes should be selected, are usually superior to individual features (e.g., genes) while considering known traditional gene-based feature selection algorithms in pathway knowledge. Pathway-based feature selection terms of predictive accuracy, stability, and biological algorithms can be classified into three major categories – interpretation [1–10]. Consequently, pathway-based penalty, stepwise forward, and weighting. Their definitions feature selection algorithms have become increasingly and characteristics are presented in Table 1. In the penalty popular and widespread. category, an additional penalty term accounting for the pathway structure/topology is added to the objective func- tion for optimization. In essence, this penalty term pro- * Correspondence: [email protected] vides some smoothness on nearby genes within a pathway, 1Division of Clinical Research, The First Hospital of Jilin University, 71Xinmin Street, Changchun, Jilin, China 130021 relying on the assumption that neighboring genes inside a 2School of Mathematics, Jilin University, 2699 Qianjin Street, Changchun, Jilin, pathway are more likely to function together or to be China 130012 Full list of author information is available at the end of the article © 2016 The Author(s). Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated. Tian et al. Biology Direct (2016) 11:50 Page 2 of 15 Table 1 Three categories of pathway-based feature selection algorithms. The filter and embedded methods are two typical types for the gene-based feature selection algorithms. As defined by [32], filter methods access the relevance of features by calculating some functional score while embedded methods search for the optimal subset simultaneously with the classifier construction Category/description Property Pathway topology information Examples [Ref.] Penalty: add an extra penalty term which Embedded feature selection methods, Need the pathway topology Net-Cox [Zhang accounts for the pathway structure to the carry out feature selection and information for all genes, e.g., et al. 2013] netSVM objective function, then optimize the coefficient estimation simultaneously, are they connected and the [Chen et al. 2011] resulting function to get the final gene subset moderate to heavy computing burden distance between them Stepwise forward: order genes based on one Usually filter methods, the beneath Usually ignore the pathway SAM-GSR specific statistic, and then add gene one by one concepts and theory are simple. However, topology information, the [Dinu et al, 2009] until there is no gain on the pre-defined score. they also inherits the filter methods’ decision hinges mainly on SurvNet [Li et al. 2012] drawbacks of inferior model parsimony the genes’ expression values and thus high false positive rate. Weighting: create some kind weights according With different weights, the chance of Account for the pathway RRFE [Johannes to the pathway knowledge and then combine those “driving” genes with subtle change topology information. et al. 2010] DRW with other feature selection methods to identify being selected increases. However, if the [Liu et al. 2013] the relevant genes estimated weights subject to big biases, the resulting model might even be inferior to those without weights. involved in the same biological process than those are far categories, while the weighting category is simpler, it has away. As a result, a ‘driving’ gene that has subtle changes been underutilized. Its underutilization might be due to but alters its neighbors’ expression values dramatically is the estimated weights being subject to errors and biases more likely to be selected. One limitation of penalization where the impact on the resulting significant may be methods is that they are associated with higher theoretical substantial. complexity and more computational efforts. In this study, we propose a hybrid method that com- The stepwise forward methods first select one gene bines SAMGSR with a pathway topology-based weight (e.g., the most significantly differentially expressed) and to carry out feature selection. As a combination of the add genes gradually, and then evaluate the performance weighting method and stepwise forward method, the of the resulting gene subset based on some statistic until objective is to address some disadvantages associated no further gain upon this statistic can be obtained. The with SAMGSR and the weighting method while utilizing SAMGSR algorithm proposed by [11] falls within this their strengths. The proposed method is referred to as category, and it consists of two steps. Its first step is weighted-SAMGSR herein. Applying it to both the simu- essentially an extension of the SAM method [12] to all lated data and real-world application, we evaluate if genes inside a pathway and the significance level of a weights reflecting gene connectivity information are pathway is determined using permutation tests. Then a valuable for feature selection. core subset is extracted from each significant pathway identified by the first step on the basis on the magni- Methods tudes of individual genes’ SAM statistics. Based on the Experimental data simulation results by us [13], SAMGSR may increase the We considered two sets of microarray data and one likelihood of those genes involved in many pathways RNA-Seq dataset in this study. One set of microarray being selected. But SAMGSR only considers a gene’s data is for a multiple sclerosis (MS) application; the pathway membership and ignores pathway topology other set and the RNA-Seq data are for a non-small cell information, it may miss those ‘driving’ genes with subtle lung cancer (NSCLC) application. changes because the inclusion of a gene in the reduced core subsets hinges on its expression difference between MS data two phenotypes. The MS application consisted of two microarray experi- The third category is to create a pathway knowledge- ments.Thefirstoneincludedchipsfromtheexperiment based weight for each gene. For instance, the reweighted E-MTAB-69 stored in the ArrayExpress [16] repository recursive feature elimination (RRFE) algorithm proposed (http://www.ebi.ac.uk/arrayexpress). All chips were hybrid- by Johannes et al. [14] uses GeneRank [15] to calculate a ized on Affymetrix HGU133 Plus 2.0 chips. In this study, rank for each gene and then weighs the coefficients in a there were 26 patients with relapsing-remitting multiple support vector machine (SVM) model by this rank. It sclerosis (RRMS) and 18 controls with neurological disor- had been demonstrated that the resulting gene signa- ders of a non-inflammatory nature. The second dataset was tures have better stability and more meaningful bio- provided by the sbv IMPROVER challenge in the year of logical interpretation [14]. Compared to the other two 2012 [17],
Load more

Recommended publications
  • The Temperature-Dependent Retention of Introns in GPI8 Transcripts Contributes to a Drooping and Fragile Shoot Phenotype in Rice
    International Journal of Molecular Sciences Article The Temperature-Dependent Retention of Introns in GPI8 Transcripts Contributes to a Drooping and Fragile Shoot Phenotype in Rice Bo Zhao 1,2, Yongyan Tang 1,2, Baocai Zhang 3, Pingzhi Wu 1, Meiru Li 1, Xinlan Xu 1, Guojiang Wu 1, Huawu Jiang 1 and Yaping Chen 1,* 1 Key Laboratory of Plant Resources Conservation and Sustainable Utilization, South China Botanical Garden, Innovation Academy for Seed Design, Chinese Academy of Sciences, Guangzhou 510650, China; [email protected] (B.Z.); [email protected] (Y.T.); [email protected] (P.W.); [email protected] (M.L.); [email protected] (X.X.); [email protected] (G.W.); [email protected] (H.J.) 2 University of Chinese Academy of Sciences, Beijing 100049, China 3 State Key Laboratory of Plant Genomics, Institute of Genetics and Developmental Biology, Chinese Academy of Sciences, Beijing 100101, China; [email protected] * Correspondence: [email protected]; Tel.: +86-20-37252750 Received: 14 November 2019; Accepted: 30 December 2019; Published: 31 December 2019 Abstract: Attachment of glycosylphosphatidylinositols (GPIs) to the C-termini of proteins is one of the most common posttranslational modifications in eukaryotic cells. GPI8/PIG-K is the catalytic subunit of the GPI transamidase complex catalyzing the transfer en bloc GPI to proteins. In this study, a T-DNA insertional mutant of rice with temperature-dependent drooping and fragile (df ) shoots phenotype was isolated. The insertion site of the T-DNA fragment was 879 bp downstream of the stop codon of the OsGPI8 gene, which caused introns retention in the gene transcripts, especially at higher temperatures.
    [Show full text]
  • Whole Genome Sequencing in an Acrodermatitis Enteropathica Family from the Middle East
    Hindawi Dermatology Research and Practice Volume 2018, Article ID 1284568, 9 pages https://doi.org/10.1155/2018/1284568 Research Article Whole Genome Sequencing in an Acrodermatitis Enteropathica Family from the Middle East Faisel Abu-Duhier,1 Vivetha Pooranachandran,2 Andrew J. G. McDonagh,3 Andrew G. Messenger,4 Johnathan Cooper-Knock,2 Youssef Bakri,5 Paul R. Heath ,2 and Rachid Tazi-Ahnini 4,6 1 Prince Fahd Bin Sultan Research Chair, Department of Medical Lab Technology, Faculty of Applied Medical Science, Prince Fahd Research Chair, University of Tabuk, Tabuk, Saudi Arabia 2Department of Neuroscience, SITraN, Te Medical School, University of Shefeld, Shefeld S10 2RX, UK 3Department of Dermatology, Royal Hallamshire Hospital, Shefeld S10 2JF, UK 4Department of Infection, Immunity and Cardiovascular Disease, Te Medical School, University of Shefeld, Shefeld S10 2RX, UK 5Biology Department, Faculty of Science, University Mohammed V Rabat, Rabat, Morocco 6Laboratory of Medical Biotechnology (MedBiotech), Rabat Medical School and Pharmacy, University Mohammed V Rabat, Rabat, Morocco Correspondence should be addressed to Rachid Tazi-Ahnini; [email protected] Received 4 April 2018; Revised 28 June 2018; Accepted 26 July 2018; Published 7 August 2018 Academic Editor: Gavin P. Robertson Copyright © 2018 Faisel Abu-Duhier et al. Tis is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. We report a family from Tabuk, Saudi Arabia, previously screened for Acrodermatitis Enteropathica (AE), in which two siblings presented with typical features of acral dermatitis and a pustular eruption but difering severity.
    [Show full text]
  • Genetic Background of Ataxia in Children Younger Than 5 Years in Finland E444
    Volume 6, Number 4, August 2020 Neurology.org/NG A peer-reviewed clinical and translational neurology open access journal ARTICLE Genetic background of ataxia in children younger than 5 years in Finland e444 ARTICLE Cerebral arteriopathy associated with heterozygous variants in the casitas B-lineage lymphoma gene e448 ARTICLE Somatic SLC35A2 mosaicism correlates with clinical fi ndings in epilepsy brain tissuee460 ARTICLE Synonymous variants associated with Alzheimer disease in multiplex families e450 Academy Officers Neurology® is a registered trademark of the American Academy of Neurology (registration valid in the United States). James C. Stevens, MD, FAAN, President Neurology® Genetics (eISSN 2376-7839) is an open access journal published Orly Avitzur, MD, MBA, FAAN, President Elect online for the American Academy of Neurology, 201 Chicago Avenue, Ann H. Tilton, MD, FAAN, Vice President Minneapolis, MN 55415, by Wolters Kluwer Health, Inc. at 14700 Citicorp Drive, Bldg. 3, Hagerstown, MD 21742. Business offices are located at Two Carlayne E. Jackson, MD, FAAN, Secretary Commerce Square, 2001 Market Street, Philadelphia, PA 19103. Production offices are located at 351 West Camden Street, Baltimore, MD 21201-2436. Janis M. Miyasaki, MD, MEd, FRCPC, FAAN, Treasurer © 2020 American Academy of Neurology. Ralph L. Sacco, MD, MS, FAAN, Past President Neurology® Genetics is an official journal of the American Academy of Neurology. Journal website: Neurology.org/ng, AAN website: AAN.com CEO, American Academy of Neurology Copyright and Permission Information: Please go to the journal website (www.neurology.org/ng) and click the Permissions tab for the relevant Mary E. Post, MBA, CAE article. Alternatively, send an email to [email protected].
    [Show full text]
  • GPI) Transamidase Subunits Phosphatidylinositol Glycan Class T And/Or GPI Anchor Attachment 1Induces Tumorigenesis and Contributes to Invasion in Human Breast Cancer
    Research Article Overexpression of Glycosylphosphatidylinositol (GPI) Transamidase Subunits Phosphatidylinositol Glycan Class T and/or GPI Anchor Attachment 1Induces Tumorigenesis and Contributes to Invasion in Human Breast Cancer Guojun Wu,1,5 Zhongmin Guo,1 Aditi Chatterjee,1 Xin Huang,6 Ethel Rubin,2 Feng Wu,3 Elizabeth Mambo,1 Xiaofei Chang,1 Motonobu Osada,1 Myoung Sook Kim,1 Chulso Moon,1 Joseph A. Califano,1 Edward A. Ratovitski,4 Susanne M. Gollin,6 Saraswati Sukumar,2 David Sidransky,1 and Barry Trink1 1Department of Otolaryngology-Head and Neck Surgery, 2Breast Cancer Program, Sidney Kimmel Comprehensive Cancer Center, 3Division of Gastroenterology, Department of Medicine, and 4Department of Dermatology, Johns Hopkins University School of Medicine, Baltimore, Maryland; 5Breast Cancer Program, Karmanos Cancer Institute, Department of Pathology, Wayne State University, Detroit, Michigan; and 6Department of Human Genetics, University of PittsburghGraduate School of Public Health, Oral Cancer Center at the University of Pittsburgh, Pittsburgh, Pennsylvania Abstract ERBB2 at the 17q12 amplicon (5), c-MYC at the 8q24 amplicon (6), Based on the oncogenic role of phosphatidylinositol glycan CCND1 at the 11q13 amplicon (7, 8), ZNF217 and CYP24 at the (PIG) class U in human tumors, we explored the role of two 20q13.2 amplicon (9–11), and PPM1D and TBX2 at the 17q23 additional subunits of the glycosylphosphatidylinositol (GPI) amplicon (12–15). Among these amplicons, 8q24, 20q11-13, and transamidase complex in human breast cancer. We found that 17q23 are frequently altered in breast cancer, the most common PIG class T(PIG-T)and GPI anchor attachment 1 (GPAA1) were cause of cancer deathin women in theWestern world (16, 17).
    [Show full text]
  • Identification of Predictive Biomarkers of Response to HSP90 Inhibitors In
    International Journal of Molecular Sciences Article Identification of Predictive Biomarkers of Response to HSP90 Inhibitors in Lung Adenocarcinoma Ángela Marrugal 1, Irene Ferrer 1,2, David Gómez-Sánchez 1,2, Álvaro Quintanal-Villalonga 3, María Dolores Pastor 4, Laura Ojeda 1, Luis Paz-Ares 1,2,5,6,*,† and Sonia Molina-Pinelo 2,4,*,† 1 H12O-CNIO Lung Cancer Clinical Research Unit, Instituto de Investigación Hospital 12 de Octubre & Centro Nacional de Investigaciones Oncológicas (CNIO), 28029 Madrid, Spain; [email protected] (Á.M.); [email protected] (I.F.); [email protected] (D.G.-S.); [email protected] (L.O.) 2 CIBERONC, Respiratory Tract Tumors Program, 28029 Madrid, Spain 3 Program in Molecular Pharmacology, Memorial Sloan Kettering Cancer Center, New York, NY 10065, USA; [email protected] 4 Institute of Biomedicine of Seville (IBIS) (HUVR, CSIC, Universidad de Sevilla), 41013 Sevilla, Spain; [email protected] 5 Medical Oncology Department, Hospital Universitario Doce de Octubre, 28041 Madrid, Spain 6 Medical School, Universidad Complutense, 28040 Madrid, Spain * Correspondence: [email protected] (L.P.-A.); [email protected] (S.M.-P.) † These authors contributed equally to this work. Abstract: Heat shock protein 90 (HSP90) plays an essential role in lung adenocarcinoma, acting as a key chaperone involved in the correct functioning of numerous highly relevant protein drivers of this disease. To this end, HSP90 inhibitors have emerged as promising therapeutic strategies, even Citation: Marrugal, Á.; Ferrer, I.; though responses to them have been limited to date. Given the need to maximize treatment efficacy, Gómez-Sánchez, D.; the objective of this study was to use isobaric tags for relative and absolute quantitation (iTRAQ)- Quintanal-Villalonga, Á.; Pastor, based proteomic techniques to identify proteins in human lung adenocarcinoma cell lines whose M.D.; Ojeda, L.; Paz-Ares, L.; basal abundances were correlated with response to HSP90 inhibitors (geldanamycin and radicicol Molina-Pinelo, S.
    [Show full text]
  • Profiling the Expression Pattern of GPI Transamidase Complex Subunits in Human Cancer
    Modern Pathology (2008) 21, 979–991 & 2008 USCAP, Inc All rights reserved 0893-3952/08 $30.00 www.modernpathology.org Profiling the expression pattern of GPI transamidase complex subunits in human cancer Jatin K Nagpal1,5, Santanu Dasgupta1,5, Sana Jadallah2, Young K Chae1, Edward A Ratovitski3, Antoun Toubaji2, George J Netto2, Toby Eagle1, Aviram Nissan4, David Sidransky1 and Barry Trink1 1Department of Otolaryngology-Head and Neck Surgery, Head and Neck Cancer Research Division, Johns Hopkins University School of Medicine, Baltimore, MD, USA; 2Department of Pathology, Johns Hopkins University School of Medicine, Baltimore, MD, USA; 3Department of Dermatology, Johns Hopkins University School of Medicine, Baltimore, MD, USA and 4Department of Surgery, Hadassah University Hospital, Mount Scopus, Jerusalem, Israel The glycosylphosphatidylinositol transamidase complex (GPIT) consists of five subunits: PIG-U, PIG-T, GPAA1, PIG-S and GPI8, and is important in attaching GPI anchors to target proteins. On the basis of our previous reports incriminating PIG-U as an oncogene in bladder cancer and PIG-T and GPAA1 as oncogenes in breast cancer, we evaluated the expression pattern of the GPIT subunits in 19 different human cancers at both mRNA and protein levels. In general, our results demonstrate a more frequent expression of GPIT subunits in cancers than in normal. Among the 19 anatomic sites compared; breast, ovary and uterus showed consistent evidence of overexpression of specific GPIT subunits. There was also overexpression of PIG-U and GPI8 in lymphoma. In addition, non-small cell lung carcinoma showed significant overexpression of the GPIT subunits as compared to small cell lung carcinoma and normal lung tissue.
    [Show full text]
  • A SARS-Cov-2 Protein Interaction Map Reveals Targets for Drug Repurposing
    Article A SARS-CoV-2 protein interaction map reveals targets for drug repurposing https://doi.org/10.1038/s41586-020-2286-9 A list of authors and affiliations appears at the end of the paper Received: 23 March 2020 Accepted: 22 April 2020 A newly described coronavirus named severe acute respiratory syndrome Published online: 30 April 2020 coronavirus 2 (SARS-CoV-2), which is the causative agent of coronavirus disease 2019 (COVID-19), has infected over 2.3 million people, led to the death of more than Check for updates 160,000 individuals and caused worldwide social and economic disruption1,2. There are no antiviral drugs with proven clinical efcacy for the treatment of COVID-19, nor are there any vaccines that prevent infection with SARS-CoV-2, and eforts to develop drugs and vaccines are hampered by the limited knowledge of the molecular details of how SARS-CoV-2 infects cells. Here we cloned, tagged and expressed 26 of the 29 SARS-CoV-2 proteins in human cells and identifed the human proteins that physically associated with each of the SARS-CoV-2 proteins using afnity-purifcation mass spectrometry, identifying 332 high-confdence protein–protein interactions between SARS-CoV-2 and human proteins. Among these, we identify 66 druggable human proteins or host factors targeted by 69 compounds (of which, 29 drugs are approved by the US Food and Drug Administration, 12 are in clinical trials and 28 are preclinical compounds). We screened a subset of these in multiple viral assays and found two sets of pharmacological agents that displayed antiviral activity: inhibitors of mRNA translation and predicted regulators of the sigma-1 and sigma-2 receptors.
    [Show full text]
  • Biochemical and Structural Characterization of the Core Subunits of Gpi Transamidase
    Wayne State University Wayne State University Dissertations 1-1-2015 Biochemical And Structural Characterization Of The orC e Subunits Of Gpi Transamidase Dilani G. Gamage Wayne State University, Follow this and additional works at: http://digitalcommons.wayne.edu/oa_dissertations Part of the Chemistry Commons Recommended Citation G. Gamage, Dilani, "Biochemical And Structural Characterization Of The orC e Subunits Of Gpi Transamidase" (2015). Wayne State University Dissertations. Paper 1132. This Open Access Dissertation is brought to you for free and open access by DigitalCommons@WayneState. It has been accepted for inclusion in Wayne State University Dissertations by an authorized administrator of DigitalCommons@WayneState. BIOCHEMICAL AND STRUCTURAL CHARACTERIZATION OF THE CORE SUBUNITS OF GPI TRANSAMIDASE by DILANI G GAMAGE DISSERTATION Submitted to the Graduate School of Wayne State University, Detroit, Michigan in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY 2015 MAJOR: CHEMISTRY (Biochemistry) Approved by: Advisor Date © COPYRIGHT BY DILANI G GAMAGE 2015 All Rights Reserved DEDICATION To my loving parents K. M. Rathnaweera and G. G. Gunasena My aunt D. C. Rathnaweera My loving husband N. G. Wijesundara My dissertation advisor Prof T. L. Hendrickson ii ACKNOWLEDGMENTS I would like to acknowledge my advisor, Professor Tamara L. Hendrickson for the constant support and advise given to me during last five years. Her mentorship, guidance and believing in me to be a good research scientist, allowed me be who I am today. With her enormous scientific knowledge and generosity I was able to learn a number of new skills and techniques. The excellent atmosphere she created in our lab reduced our working stress.
    [Show full text]
  • POSITIVE RESULT Pathogenic Variant Identified
    CENTOGENE AG Am Strande 7 • 18055 Rostock • Germany xxx Order no.: xxx Order received: xxx Sample type: blood, EDTA Sample collection date: xxx Report date: xxx Report type: Final Report Patient no.: xxx, First Name: xxx, Last Name: xxx DOB: xxx, Sex: male, Your ref.: xxx Additional report recipient(s): xxx Test(s) requested: CentoGenome® CLINICAL INFORMATION Abnormal facial shape; Abnormality of the eye; Abnormality of the musculature; Abnormality of the nervous system; Abnormality of the skeletal system; Anteverted ears; Arachnodactyly; Broad-based gait; Congenital onset; Decreased muscle mass; Global developmental delay; Hearing impairment; High, narrow palate; Hyperactive deep tendon reflexes; Joint hypermobility; Long face; Long nose; Microphthalmia; Myopathic facies; Narrow chest; Ophthalmoplegia; Protruding ear; Protruding tongue; Rod-cone dystrophy; Spasticity; Tall chin; Wide nasal bridge (Clinical information indicated above follows HPO nomenclature.) Family history: Yes. Consanguineous parents: Yes. We performed sequencing analysis focusing on the phenotype of this patient. Please see our concurrent reports xxx, and xxx.. POSITIVE RESULT Pathogenic variant identified INTERPRETATION A homozygous pathogenic variant was identified in the AHI1 gene. A genetic diagnosis of autosomal recessive Joubert syndrome type 3 is confirmed. RECOMMENDATIONS Genetic counselling is recommended. > Contact Details Tel.: +49 (0)381 80113 416 CLIA registration 99D2049715; CAP registration 8005167. Scientific use of Fax: +49 (0)381 80113 401 these results requires permission of CENTOGENE. If you would like to download your reports from our web portal, please contact us to receive [email protected] your login and password. More information is available at www.centogene.com www.centogene.com or [email protected].
    [Show full text]
  • GPI) Transamidase Subunits Phosphatidylinositol Glycan Class T And/Or GPI Anchor Attachment 1Induces Tumorigenesis and Contributes to Invasion in Human Breast Cancer
    Research Article Overexpression of Glycosylphosphatidylinositol (GPI) Transamidase Subunits Phosphatidylinositol Glycan Class T and/or GPI Anchor Attachment 1Induces Tumorigenesis and Contributes to Invasion in Human Breast Cancer Guojun Wu,1,5 Zhongmin Guo,1 Aditi Chatterjee,1 Xin Huang,6 Ethel Rubin,2 Feng Wu,3 Elizabeth Mambo,1 Xiaofei Chang,1 Motonobu Osada,1 Myoung Sook Kim,1 Chulso Moon,1 Joseph A. Califano,1 Edward A. Ratovitski,4 Susanne M. Gollin,6 Saraswati Sukumar,2 David Sidransky,1 and Barry Trink1 1Department of Otolaryngology-Head and Neck Surgery, 2Breast Cancer Program, Sidney Kimmel Comprehensive Cancer Center, 3Division of Gastroenterology, Department of Medicine, and 4Department of Dermatology, Johns Hopkins University School of Medicine, Baltimore, Maryland; 5Breast Cancer Program, Karmanos Cancer Institute, Department of Pathology, Wayne State University, Detroit, Michigan; and 6Department of Human Genetics, University of PittsburghGraduate School of Public Health, Oral Cancer Center at the University of Pittsburgh, Pittsburgh, Pennsylvania Abstract ERBB2 at the 17q12 amplicon (5), c-MYC at the 8q24 amplicon (6), Based on the oncogenic role of phosphatidylinositol glycan CCND1 at the 11q13 amplicon (7, 8), ZNF217 and CYP24 at the (PIG) class U in human tumors, we explored the role of two 20q13.2 amplicon (9–11), and PPM1D and TBX2 at the 17q23 additional subunits of the glycosylphosphatidylinositol (GPI) amplicon (12–15). Among these amplicons, 8q24, 20q11-13, and transamidase complex in human breast cancer. We found that 17q23 are frequently altered in breast cancer, the most common PIG class T(PIG-T)and GPI anchor attachment 1 (GPAA1) were cause of cancer deathin women in theWestern world (16, 17).
    [Show full text]
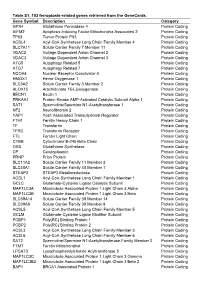
  • Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
    Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein
    [Show full text]
  • Genome-Wide Association Study and Pathway Analysis for Female Fertility Traits in Iranian Holstein Cattle
    Ann. Anim. Sci., Vol. 20, No. 3 (2020) 825–851 DOI: 10.2478/aoas-2020-0031 GENOME-WIDE ASSOCIATION STUDY AND PATHWAY ANALYSIS FOR FEMALE FERTILITY TRAITS IN IRANIAN HOLSTEIN CATTLE Ali Mohammadi1, Sadegh Alijani2♦, Seyed Abbas Rafat2, Rostam Abdollahi-Arpanahi3 1Department of Genetics and Animal Breeding, University of Tabriz, Tabriz, Iran 2Department of Animal Science, Faculty of Agriculture, University of Tabriz, Tabriz, Iran 3Department of Animal Science, University College of Abureyhan, University of Tehran, Tehran, Iran ♦Corresponding author: [email protected] Abstract Female fertility is an important trait that contributes to cow’s profitability and it can be improved by genomic information. The objective of this study was to detect genomic regions and variants affecting fertility traits in Iranian Holstein cattle. A data set comprised of female fertility records and 3,452,730 pedigree information from Iranian Holstein cattle were used to predict the breed- ing values, which were then employed to estimate the de-regressed proofs (DRP) of genotyped animals. A total of 878 animals with DRP records and 54k SNP markers were utilized in the ge- nome-wide association study (GWAS). The GWAS was performed using a linear regression model with SNP genotype as a linear covariate. The results showed that an SNP on BTA19, ARS-BFGL- NGS-33473, was the most significant SNP associated with days from calving to first service. In total, 69 significant SNPs were located within 27 candidate genes. Novel potential candidate genes include OSTN, DPP6, EphA5, CADPS2, Rfc1, ADGRB3, Myo3a, C10H14orf93, KIAA1217, RBPJL, SLC18A2, GARNL3, NCALD, ASPH, ASIC2, OR3A1, CHRNB4, CACNA2D2, DLGAP1, GRIN2A and ME3.
    [Show full text]