DOCSLIB.ORG

Approximation of the Series ∑ Where A,B,C ∈ R With

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Approximation of the Series ∑ Where A,B,C ∈ R With International Journal of Mathematics Research. ISSN 0976-5840 Volume 9, Number 1 (2017), pp. 1-4 © International Research Publication House http://www.irphouse.com (−1)푛−1 Approximation of the Series ∑∞ 푛=1 푎푛2+푏푛+푐 where a,b,c ∈ R with a≠0 Kumari Sreeja S. Nair and Dr. V. Madhukar Mallayya 1Assistant Professor, Department of Mathematics Govt. Arts College, Thiruvananthapuram, Kerala, India. 2Former Professor and Head, Department of Mathematics Mar Ivanios College, Thiruvananthapuram, Kerala, India. Abstract Here we give approximation of an alternating series using remainder term of the series. Here we introduce a new term called correction term. The correction term plays a vital role in series approximation. Keywords: Correction function, error function, remainder term, alternating series, rational approximation, Dirichlet’s series. INTRODUCTION The illusturious mathematician Madhava of 14th century introduces correction function for the series for pi. The Madhava series is 4푑 4푑 4푑 ..................... 푛−1 4푑 푛 4푑(2푛)/2 C = − + − +(−1) + (−1) , where C is the 1 3 5 2푛−1 (2푛)2+1 circumference of a circle of diameter d. n (2푛)/2 Here the remainder term is (-1) 4d Gn where Gn = is the correction (2푛)2+1 term. The introduction of the correction term improves the value of C and gives a better approximation for it. 2 Kumari Sreeja S. Nair and Dr. V. Madhukar Mallayya (−1)푛−1 RATIONAL APPROXIMATION OF ALTERNATING SERIES ∑∞ 푛=1 푎푛2+푏푛+푐 where a,b,c ∈ R with a≠0 and √푏2 − 4푎푐 ≠ 2a. (−1)푛−1 The alternating series ∑∞ satisfies the conditions of alternating series 푛=1 푎푛2+푏푛+푐 test and so it is convergent. Theorem (−1)푛−1 The correction function for the alternating series ∑∞ where a,b,c ∈ R with 푛=1 푎푛2+푏푛+푐 1 a≠ 0 is Gn = {2푎푛2+(2푏+2푎)푛+(2푐+푏+2푎)} Proof If Gn is the correction function after n terms of the series ,then 1 we have Gn + Gn+1 = 푎푛2+(2푎+푏)푛+푎+푏+푐 1 The error function is En = Gn + Gn+1 − 푎푛2+(2푎+푏)푛+푎+푏+푐 1 Let Gn (푟1 , 푟2) = 2 where 푟1 , 푟2 ∈ R and {2푎푛 +(4푎+2푏)푛+(2푎+2푏+2푐)}−(푟1 푛+푟2) n is fixed. Then error function |퐸푛(푟1, 푟2)| is minimum for r1 = 2a , r2 = b Hence for r1 = 2a , r2 = b , both Gn and En are functions of a single variable n. 푛−1 ∞ (−1) Thus the correction function for the series ∑ is 푛=1 푎푛2+푏푛+푐 1 Gn = {2푎푛2+(2푏+2푎)푛+(2푐+푏+2푎)} The corresponding error function is |(푏2−4푎푐)−4푎2| |En | = {2푎푛2+(2푏+2푎)푛+(2푐+푏+2푎)}{(2푎푛2+(2푏+6푎)푛+(6푎+3푏+2푐)}{(푎푛2+(2푎+푏)푛+(푎+푏+푐)} Hence the proof. Approximation of the Series 3 REMARK th Clearly Gn is less than the absolute value of the (n+1) term. APPLICATION 풏−ퟏ ∞ (−ퟏ) 1. The series ∑ = ᶯ(ퟐ) 풏=ퟏ 풏ퟐ We have ᶯ(2) = 0.8224670334, using a calculator. 1 The correction function for the series is Gn = 2푛2+2푛+2 For n= 10 , the series approximation after applying correction function is given below 푛 Number of terms Sn Sn + (−1) Gn 10 0.8179621756 0.82246666801 (−1)푛−1 2. THE ALTERNATING SERIES ∑∞ 푛=1 푛(푛+1) (−1)푛−1 The alternating series ∑∞ is convergent and converges to 2log2-1. 푛=1 푛(푛+1) We have 2log2-1 = 0.3862943611, using a calculator. 1 The correction function for the series is Gn = 2(푛+1)2+12 For n= 10 , the series approximation after applying correction function is given below 푛 Number of terms Sn Sn + (−1) Gn 10 0.3821789321 0.3863283098 CONCLUSION The introduction of correction function improves the sum of the series and gives a better approximation. 4 Kumari Sreeja S. Nair and Dr. V. Madhukar Mallayya REFERENCES [1] Dr. Konrad Knopp - Theory and Application of Infinite series - Blackie and son limited (London and Glasgow) [2] Sankara and Narayana, Lilavati of Bhaskaracharya with the Kriyakramakari, an elaborate exposition of the rationale with introduction and appendices (ed) K.VSarma (Visvesvaranand Vedic Research Institute, Hoshiarpur) 1975, p, 386-391. [3] Dr. V.Madhukar Mallayya- Proceedings of the Conference on Recent Trends in Mathematical Analysis- © 2003, Allied Publishers Pvt. Ltd. ISBN 81-7764- 399-1 [4] A Course of Pure Mathematics - G.H.Hardy (tenth edition) Cambridge at the university press 1963 [5] K. Knopp, Infinite sequences .and series, Dover-1956 [6] T.Hayashi, T.K.Kusuba and M.Yano, Centaururs,33,149,1990 [7] Yuktidipika of Sankara (commentary on Tantrasangraha), ed. K.V.Sarma, Hoshiarpur 1977 .
Load more

Recommended publications
  • Bhaskara's Approximation to and Madhava's Series for Sine
    Ursinus College Digital Commons @ Ursinus College Transforming Instruction in Undergraduate Calculus Mathematics via Primary Historical Sources (TRIUMPHS) Winter 2020 Bhaskara's Approximation to and Madhava's Series for Sine Kenneth M. Monks [email protected] Follow this and additional works at: https://digitalcommons.ursinus.edu/triumphs_calculus Click here to let us know how access to this document benefits ou.y Recommended Citation Monks, Kenneth M., "Bhaskara's Approximation to and Madhava's Series for Sine" (2020). Calculus. 15. https://digitalcommons.ursinus.edu/triumphs_calculus/15 This Course Materials is brought to you for free and open access by the Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) at Digital Commons @ Ursinus College. It has been accepted for inclusion in Calculus by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. Bh¯askara's Approximation to and M¯adhava's Series for Sine Kenneth M Monks∗ May 20, 2021 A chord is a very natural construction in geometry; it is the line segment obtained by connecting two points on a circle. Chords were studied extensively in ancient Greek geometry. For example, Euclid's Elements [Euclid, c. 300 BCE] contains plenty of theorems relating the circle's arc AB to the line segment AB (shown below).1 A B Indian mathematicians, motivated by astronomy, were the first to specifically calculate values of half-chords instead [Gupta, 1967, p. 121]. This work led very directly to the function which we call sine today. Task 1 Half-chords and sine. Suppose the circle above has radius 1.
    [Show full text]
  • Kamala¯Kara Commentary on the Work, Called Tattvavivekodāharan
    K related to the Siddhānta-Tattvaviveka, one a regular Kamala¯kara commentary on the work, called Tattvavivekodāharan. a, and the other a supplement to that work, called Śes.āvasanā, in which he supplied elucidations and new K. V. SARMA material for a proper understanding of his main work. He held the Sūryasiddhānta in great esteem and also wrote a Kamalākara was one of the most erudite and forward- commentary on that work. looking Indian astronomers who flourished in Varanasi Kamalākara was a critic of Bhāskara and his during the seventeenth century. Belonging to Mahar- Siddhāntaśiroman. i, and an arch-rival of Munīśvara, a ashtrian stock, and born in about 1610, Kamalākara close follower of Bhāskara. This rivalry erupted into came from a long unbroken line of astronomers, bitter critiques on the astronomical front. Thus Ranga- originally settled at the village of Godā on the northern nātha, younger brother of Kamalākara, wrote, at the . banks of the river Godāvarī. Towards AD 1500, the insistence of the latter, a critique on Munīśvara’s Bhangī family migrated to Varanasi and came to be regarded as method (winding method) of true planets, entitled . reputed astronomers and astrologers. Kamalākara Bhangī-vibhangī (Defacement of the Bhangi), to which . studied traditional Hindu astronomy under his elder Munīśvara replied with a Khand.ana (Counter). Munīś- brother Divākara, but extended the range of his studies vara attacked the theory of precession advocated by to Islamic astronomy, particularly to the school of Kamalākara, and Ranganātha refuted the criticisms of his Ulugh Beg of Samarkand. He also studied Greek brother in his Loha-gola-khan.
    [Show full text]
  • BOOK REVIEW a PASSAGE to INFINITY: Medieval Indian Mathematics from Kerala and Its Impact, by George Gheverghese Joseph, Sage Pu
    HARDY-RAMANUJAN JOURNAL 36 (2013), 43-46 BOOK REVIEW A PASSAGE TO INFINITY: Medieval Indian Mathematics from Kerala and its impact, by George Gheverghese Joseph, Sage Publications India Private Limited, 2009, 220p. With bibliography and index. ISBN 978-81-321-0168-0. Reviewed by M. Ram Murty, Queen's University. It is well-known that the profound concept of zero as a mathematical notion orig- inates in India. However, it is not so well-known that infinity as a mathematical concept also has its birth in India and we may largely credit the Kerala school of mathematics for its discovery. The book under review chronicles the evolution of this epoch making idea of the Kerala school in the 14th century and afterwards. Here is a short summary of the contents. After a brief introduction, chapters 2 and 3 deal with the social and mathematical origins of the Kerala school. The main mathematical contributions are discussed in the subsequent chapters with chapter 6 being devoted to Madhava's work and chapter 7 dealing with the power series for the sine and cosine function as developed by the Kerala school. The final chapters speculate on how some of these ideas may have travelled to Europe (via Jesuit mis- sionaries) well before the work of Newton and Leibniz. It is argued that just as the number system travelled from India to Arabia and then to Europe, similarly many of these concepts may have travelled as methods for computational expediency rather than the abstract concepts on which these algorithms were founded. Large numbers make their first appearance in the ancient writings like the Rig Veda and the Upanishads.
    [Show full text]
  • Global Positioning System (GPS)
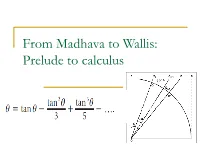
    From Madhava to Wallis: Prelude to calculus Madhava and the Kerala school There is now considerable documentary evidence that many of the ideas needed for the development of calculus were already written down by what is now called the Kerala school of mathematics in south western India in the 14th century. Madhava (1340-1425 CE) was the foremost member of this school who developed the theory of the trigonometric functions and derived the familiar Taylor series expansions for them. His work was described in detail with proofs by Jyesthadeva who wrote the text called Yuktibhasha in the middle of the 16th century. Madhava series for the trigonometric functions Studying the sine and cosine function, Madhava derived the following well-known formulas: The last is the famous arctan series re-discovered by Gregory several centuries later. When θ=π/4, we get the famous Madhava-Gregory-Leibniz series for π. The series for arctan x Evaluation of the sum The migration of ideas and Father Mersenne According to George Joseph, author of the Crest of the Peacock, it is quite possible that many of the ideas of the Kerala school migrated through Jesuit missionaries to Europe. Most notable among the Jesuits was Father Marin Mersenne (1588-1648) who was a close friend of both Descartes and Fermat (in fact, many conjectures attributed to Fermat appear in his letters to Mersenne). Thus many of the ideas of calculus were “in the air”. The work of Cavalieri, Fermat, Mengoli and Gregory Mengoli and log 2 Mengoli discovered that 1-1/2 + 1/3 -1/4 + … converges to log 2.
    [Show full text]
  • Approximation of Alternating Series Using Correction Function and Error Function
    International Journal of Scientific and Innovative Mathematical Research (IJSIMR) Volume 4, Issue 8, August 2016, PP 24-26 ISSN 2347-307X (Print) & ISSN 2347-3142 (Online) DOI: http://dx.doi.org/10.20431/2347-3142.0408004 www.arcjournals.org Approximation of Alternating Series using Correction Function and Error Function Kumari Sreeja S Nair Dr.V.Madhukar Mallayya Assistant Professor of Mathematics Former Professor and Head Govt.Arts College, Thiruvananthapuram, Department of Mathematics Kerala, India Mar Ivanios College Thiruvananthapuram, India Abstract: In this paper we give a rational approximation of an alternating series using remainder term of the series. For that we shall introduce a correction function to the series. The correction function plays a vital role in series approximation. Using correction function we shall deduce an error function to the series. Keywords: Correction function, error function, remainder term, alternating series, Madhava series, rational approximation. 1. INTRODUCTION In 14푡ℎ century, the Indian mathematician Madhava gave an approximation of the pi series using remainder term of the series. Madhava series is, 4푑 4푑 4푑 ..................... 푛−1 4푑 푛 4푑(2푛)/2 C = − + − +(−1) + (−1) , where C is the circumference of a 1 3 5 2푛−1 2푛 2+1 (2푛)/2 circle of diameter d. Here the remainder term is (-1)n 4d G where G = is the correction n n 2푛 2+1 function. The introduction of the correction term gives a better approximation of the series. 2. METHOD 푛−1 ∞ (−1) APPROXIMATION OF THE ALTERNATING SERIES 푛=1 푛 푛+1 (푛+2) (−1)푛−1 The alternating series ∞ satisfies the conditions of alternating series test and so it is 푛=1 푛 푛+1 (푛+2) convergent.
    [Show full text]
  • JETIR Research Journal
    © 2020 JETIR November 2020, Volume 7, Issue 11 www.jetir.org (ISSN-2349-5162) Exploring the Algebraic and Geometric Nature of 흅. 1*Archisman Roy, 2Tushar Banerjee 1Author (Student), AOSHS, Higher Secondary School of Science; 2Research Scholar, SSSUTMS 1Department of Science, 2Department of Zoology 1Asansol, India. * denotes correspondence Abstract: This bodacious study has been endeavored to probe different natures of π. Π comes from the Greek script of the word ‘periphery’ which means circumference. In connection to that π has a birthright for claiming geometry as its origin. Metaphorically, it is a real and definite number which is algebraically inexpressible. Our piece of research is thus willing to persuade that every geometric relation can be expressed with some equations of algebra and each algebraic expansion has its geometric interpretation. In addition to that, the article produces numerously validated as well as cited works of famous mathematicians to cajole about the article's plausibility. It approaches a good deal of mathematical history for congenially maintaining its engagement with the content. Sufficient statistical data have been produced to sway every bit of the mathematical perspective. The piece of writing consists of suitable graphs and images adhering to its requirement. Furthermore, it expresses enthusiastically about its new substantial contribution regarding the cognizance of π. Finally, the article suffers a lenient way of producing π subsequently through three stages of visualizing a mathematical paradox viz geometric background, augmentation of algebra, and the real connection between them both. Index Terms - Irrational, constant, transcendental, infinite-fraction, exact. I. INTRODUCTION The world of algebraical mathematics especially the number theorems are gigantically fascinated by a few irrational numbers such as Euler's constant 'e' and the 'π'.
    [Show full text]
  • Introduction to Scientific Computing
    Introduction to Scientific Computing with Maple Programming Zhonggang Zeng c 2009 with contributions from David Rutschman August 23, 2015 Contents Table of Contents i Scientific Computing Index iv 1 Fundamentals 1 1.1 Maplecommandlines............................... 2 1.2 Simpleprogramming ............................... 10 1.3 Conditionalstatements-Branching . .. 18 1.4 Commonerrors .................................. 23 1.5 WritingaprojectreportonaMapleworksheet . ... 24 1.6 Exercises...................................... 24 1.7 Projects ...................................... 30 2 Loops. Part I 33 2.1 The“for-do”loop................................. 33 2.2 Iteration...................................... 35 2.2.1 Newton’s iteration (Numerical Analysis ) ................. 37 2.2.2 Chaotic map (Dynamic System ) ...................... 38 2.2.3 Continuous fractions (Number Theory ) .................. 39 2.2.4 Continuous fractions, revisited . 40 2.3 Recursivesummation............................... 41 2.3.1 Taylor series (Approximation Theory ) ................... 42 2.3.2 Quadrature (Numerical Analysis ) ..................... 44 2.3.3 Nested sums and products (Elementary Algebra ) ............ 45 2.4 Exploring scientific computing . 47 2.4.1 Fourier series (Fourier Analysis ) ..................... 47 2.4.2 Solving congruences (Number Theory ) ................... 48 2.5 Exercise ...................................... 49 2.6 Projects ...................................... 58 3 Loops. Part II 61 3.1 The“while-do”loop ..............................
    [Show full text]
  • Rapidly Convergent Series from Gregory Series 1
    International J. of Math. Sci. & Engg. Appls. (IJMSEA) ISSN 0973-9424, Vol. 11 No. I (April, 2017), pp. 171-175 RAPIDLY CONVERGENT SERIES FROM GREGORY SERIES KUMARI SREEJA S. NAIR1 AND Dr. MARY GEORGE2 1 Assistant Professor of Mathematics, Govt.Arts College, Thiruvananthapuram, Kerala, India 2 Associative Professor and Head, Department of Mathematics, Mar Ivanios College, Thiruvananthapuram, India Abstract In this paper we shall extract a rapidly convergent series from a given series, by applying a correction function to the series. Hence the rate of convergence of the new series can be increased. 1. Introduction The approximation of an alternating series can be done using remainder term of the series. The absolute value of the remainder term is the correction function. The in- troduction of correction function certainly improves the sum of the series and gives a better approximation for it. We can also deduce some rapidly convergent series using correction function and the corresponding error functions. The new series so extracted increases the rate of convergence of the series. −−−−−−−−−−−−−−−−−−−−−−−−−−−− Key Words : Remainder term, Alternating series, Madhava series, Rate of convergence, Rapidly convergent series. c http: //www.ascent-journals.com 171 172 KUMARI SREEJA S. NAIR & Dr. MARY GEORGE 2. Preliminary Definitions 1 P n−1 Definition 1 : An alternating series is an infinite series of the form (−) an where n=1 the terms an > 0: 1 P n−1 Definition 2 : The remainder term for an alternating series (−) an is the sum n=1 of the series after n terms. It is denoted by Rn. 1 P k−1 i.e.
    [Show full text]
  • Sources in the Development of Mathematics
    This page intentionally left blank Sources in the Development of Mathematics The discovery of infinite products by Wallis and infinite series by Newton marked the beginning of the modern mathematical era. The use of series allowed Newton to find the area under a curve defined by any algebraic equation, an achievement completely beyond the earlier methods of Torricelli, Fermat, and Pascal. The work of Newton and his contemporaries, including Leibniz and the Bernoullis, was concentrated in math- ematical analysis and physics. Euler’s prodigious mathematical accomplishments dramatically extended the scope of series and products to algebra, combinatorics, and number theory. Series and products proved pivotal in the work of Gauss, Abel, and Jacobi in elliptic functions; in Boole and Lagrange’s operator calculus; and in Cayley, Sylvester, and Hilbert’s invariant theory. Series and products still play a critical role in the mathematics of today. Consider the conjectures of Langlands, including that of Shimura-Taniyama, leading to Wiles’s proof of Fermat’s last theorem. Drawing on the original work of mathematicians from Europe, Asia, and America, Ranjan Roy discusses many facets of the discovery and use of infinite series and products. He gives context and motivation for these discoveries, including original notation and diagrams when practical. He presents multiple derivations for many important theorems and formulas and provides interesting exercises, supplementing the results of each chapter. Roy deals with numerous results, theorems, and methods used by students, mathematicians, engineers, and physicists. Moreover, since he presents original math- ematical insights often omitted from textbooks, his work may be very helpful to mathematics teachers and researchers.
    [Show full text]
  • The Development of Calculus in the Kerala School
    The Mathematics Enthusiast Volume 11 Number 3 Number 3 Article 5 12-2014 The development of Calculus in the Kerala School Phoebe Webb Follow this and additional works at: https://scholarworks.umt.edu/tme Part of the Mathematics Commons Let us know how access to this document benefits ou.y Recommended Citation Webb, Phoebe (2014) "The development of Calculus in the Kerala School," The Mathematics Enthusiast: Vol. 11 : No. 3 , Article 5. Available at: https://scholarworks.umt.edu/tme/vol11/iss3/5 This Article is brought to you for free and open access by ScholarWorks at University of Montana. It has been accepted for inclusion in The Mathematics Enthusiast by an authorized editor of ScholarWorks at University of Montana. For more information, please contact [email protected]. TME, vol. 11, no. 3, p. 495 The Development of Calculus in the Kerala School Phoebe Webb1 University of Montana Abstract: The Kerala School of mathematics, founded by Madhava in Southern India, produced many great works in the area of trigonometry during the fifteenth through eighteenth centuries. This paper focuses on Madhava's derivation of the power series for sine and cosine, as well as a series similar to the well-known Taylor Series. The derivations use many calculus related concepts such as summation, rate of change, and interpolation, which suggests that Indian mathematicians had a solid understanding of the basics of calculus long before it was developed in Europe. Other evidence from Indian mathematics up to this point such as interest in infinite series and the use of a base ten decimal system also suggest that it was possible for calculus to have developed in India almost 300 years before its recognized birth in Europe.
    [Show full text]
  • Collection of Series for Π
    Collection of series for π Pascal Sebah and Xavier Gourdon numbers.computation.free.fr/Constants/constants.html March 31, 2004 Abstract Selection of some of the numerous series expansion involving the fa- mous constant π. 1 Introduction There are a great many numbers of series involving the constant π,weprovide a selection. The celebrated Swiss mathematician Leonhard Euler (1707-1783) discovered many of those. 2 Around Leibniz-Gregory-Madhava series π 1 1 1 =1− + − + ··· (Leibniz-Gregory-Madhava) 4 3 5 7 π2 − k ( 1) 1 ··· 1 = k 1+ + + k (Knopp) 16 k≥0 +1 3 2 +1 π 3 1 1 1 = + − + −··· (Nilakantha) 4 4 2.3.4 4.5.6 6.7.8 π 1 1.2 1.2.3 =1+ + + + ··· (Euler) 2 3 3.5 3.5.7 π 1.2 1.2.3 1.2.3.4 = + + + ··· 2 1.3 1.3.5 1.3.5.7 k − π 3 1ζ k = k ( + 1) (Flajolet-Vardi) k≥1 4 π 1 = arctan k2 k (Knopp) 4 k≥1 + +1 π 1 = arctan F2k+1 4 k≥1 1 1 1 π π = k+1 tan k+1 (Euler) k≥1 2 2 √ π 2 1 1 1 1 1 =1+ − − + + −··· √4 3 5 7 9 11 π 3 1 1 1 1 1 =1− + − + − + ··· √6 5 7 11 13 17 π 3 1 1 1 1 1 =1− + − + − + ··· √9 2 4 5 7 8 π 3 (−1)k = k k (Sharp) 6 k≥0 3 (2 +1) The Fn are Fibonacci numbers. F0 =0,F1 =1,F2 =1,F3 =2,F4 =3,F5 =5, ..., Fn+1 = Fn + Fn−1.
    [Show full text]
  • Infinite Series, Infinite Products, and Infinite Fractions
    Part 3 Infinite series, infinite products, and infinite fractions CHAPTER 5 Advanced theory of infinite series Even as the finite encloses an infinite series And in the unlimited limits appear, So the soul of immensity dwells in minutia And in the narrowest limits no limit in here. What joy to discern the minute in infinity! The vast to perceive in the small, what divinity! Jacob Bernoulli (1654-1705) Ars Conjectandi. This chapter is about going in-depth into the theory and application of infinite series. One infinite series that will come up again and again in this chapter and the next chapter as well, is the Riemann zeta function 1 1 ζ(z) = ; nz n=1 X introduced in Section 4.6. Amongst many other things, in this chapter we'll see how to write some well-known constants in terms of the Riemann zeta function; e.g. we'll derive the following neat formula for our friend log 2 ( 5.5): x 1 1 log 2 = ζ(n); 2n n=2 X another formula for our friend the Euler-Mascheroni constant ( 5.9): x 1 ( 1)n γ = − ζ(n); n n=2 X and two more formulas involving our most delicious friend π (see 's 5.10 and 5.11): x 1 3n 1 π2 1 1 1 1 1 π = − ζ(n + 1) ; = ζ(2) = = 1 + + + + : 4n 6 n2 22 32 42 · · · n=2 n=1 X X In this chapter, we'll also derive Gregory-Leibniz-Madhava's formula ( 5.10) x π 1 1 1 1 1 = 1 + + + ; 4 − 3 5 − 7 9 − 11 − · · · and Machin's formula which started the \decimal place race" of computing π ( 5.10): x 1 1 1 ( 1)n 4 1 π = 4 arctan arctan = 4 − : 5 − 239 (2n + 1) 52n+1 − 2392n+1 n=0 X 229 230 5.
    [Show full text]