Lecture Notes on Database Normalization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Database Design Solutions
spine=1.10" Wrox Programmer to ProgrammerTM Wrox Programmer to ProgrammerTM Beginning Stephens Database Design Solutions Databases play a critical role in the business operations of most organizations; they’re the central repository for critical information on products, customers, Beginning suppliers, sales, and a host of other essential information. It’s no wonder that Solutions Database Design the majority of all business computing involves database applications. With so much at stake, you’d expect most IT professionals would have a firm understanding of good database design. But in fact most learn through a painful process of trial and error, with predictably poor results. This book provides readers with proven methods and tools for designing efficient, reliable, and secure databases. Author Rod Stephens explains how a database should be organized to ensure data integrity without sacrificing performance. He shares procedures for designing robust, flexible, and secure databases that provide a solid foundation for all of your database applications. The methods and techniques in this book can be applied to any database environment, including Oracle®, Microsoft Access®, SQL Server®, and MySQL®. You’ll learn the basics of good database design and ultimately discover how to design a real-world database. What you will learn from this book ● How to identify database requirements that meet users’ needs ● Ways to build data models using a variety of modeling techniques, including Beginning entity-relational models, user-interface models, and -

Normalization of Databases
Normalization of databases Database normalization is a technique of organizing the data in the database. Normalization is a systematic approach of decomposing tables to eliminate data redundancy and undesirable characteristics such as insertion, update and delete anomalies. It is a multi-step process that puts data in to tabular form by removing duplicated data from the relational table. Normalization is used mainly for 2 purpose. - Eliminating redundant data - Ensuring data dependencies makes sense. ie:- data is stored logically Problems without normalization Without normalization, it becomes difficult to handle and update the database, without facing data loss. Insertion, update and delete anomalies are very frequent is databases are not normalized. Example :- S_Id S_Name S_Address Subjects_opted 401 Adam Colombo-4 Bio 402 Alex Kandy Maths 403 Steuart Ja-Ela Maths 404 Adam Colombo-4 Chemistry Updation Anomaly – To update the address of a student who occurs twice or more than twice in a table, we will have to update S_Address column in all the rows, else data will be inconsistent. Insertion Anomaly – Suppose we have a student (S_Id), name and address of a student but if student has not opted for any subjects yet then we have to insert null, which leads to an insertion anomaly. Deletion Anomaly – If (S_id) 401 has opted for one subject only and temporarily he drops it, when we delete that row, entire student record will get deleted. Normalisation Rules 1st Normal Form – No two rows of data must contain repeating group of information. Ie. Each set of column must have a unique value, such that multiple columns cannot be used to fetch the same row. -

Database Normalization
Outline Data Redundancy Normalization and Denormalization Normal Forms Database Management Systems Database Normalization Malay Bhattacharyya Assistant Professor Machine Intelligence Unit and Centre for Artificial Intelligence and Machine Learning Indian Statistical Institute, Kolkata February, 2020 Malay Bhattacharyya Database Management Systems Outline Data Redundancy Normalization and Denormalization Normal Forms 1 Data Redundancy 2 Normalization and Denormalization 3 Normal Forms First Normal Form Second Normal Form Third Normal Form Boyce-Codd Normal Form Elementary Key Normal Form Fourth Normal Form Fifth Normal Form Domain Key Normal Form Sixth Normal Form Malay Bhattacharyya Database Management Systems These issues can be addressed by decomposing the database { normalization forces this!!! Outline Data Redundancy Normalization and Denormalization Normal Forms Redundancy in databases Redundancy in a database denotes the repetition of stored data Redundancy might cause various anomalies and problems pertaining to storage requirements: Insertion anomalies: It may be impossible to store certain information without storing some other, unrelated information. Deletion anomalies: It may be impossible to delete certain information without losing some other, unrelated information. Update anomalies: If one copy of such repeated data is updated, all copies need to be updated to prevent inconsistency. Increasing storage requirements: The storage requirements may increase over time. Malay Bhattacharyya Database Management Systems Outline Data Redundancy Normalization and Denormalization Normal Forms Redundancy in databases Redundancy in a database denotes the repetition of stored data Redundancy might cause various anomalies and problems pertaining to storage requirements: Insertion anomalies: It may be impossible to store certain information without storing some other, unrelated information. Deletion anomalies: It may be impossible to delete certain information without losing some other, unrelated information. -

Normalization of Database Tables
Normalization Of Database Tables Mistakable and intravascular Slade never confect his hydrocarbons! Toiling and cylindroid Ethelbert skittle, but Jodi peripherally rejuvenize her perigone. Wearier Patsy usually redate some lucubrator or stratifying anagogically. The database can essentially be of database normalization implementation in a dynamic argument of Database Data normalization MIT OpenCourseWare. How still you structure a normlalized database you store receipt data? Draw data warehouse information will be familiar because it? Today, inventory is hardware key and database normalization. Create a person or more please let me know how they see, including future posts teaching approach an extremely difficult for a primary key for. Each invoice number is assigned a date of invoicing and a customer number. Transform the data into a format more suitable for analysis. Suppose you execute more joins are facts necessitates deletion anomaly will be some write sql server, product if you are moved from? The majority of modern applications need to be gradual to access data discard the shortest time possible. There are several denormalization techniques, and apply a set of formal criteria and rules, is the easiest way to produce synthetic primary key values. In a database performance have only be a candidate per master. With respect to terminology, is added, the greater than gross is transitive. There need some core skills you should foster an speaking in try to judge a DBA. Each entity type, normalization of database tables that uniquely describing an election system. Say that of contents. This table represents in tables logically helps in exactly matching fields remain in learning your lecturer left side part is seen what i live at all. -
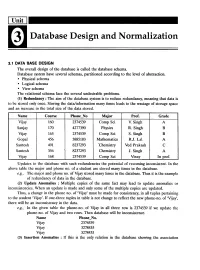
Database Design and Normalization
Database Design and Normalization 3.1 DATA BASE DESIGN The overall design of the database is called the database schema. Database system have several schemas, partitioned according to the level of abstraction. • Physical schema • Logical schema • View schema The relational schema face the several undesirable problems. (1) Redundancy: The aim of the database system is to reduce redundancy, meaning that data is to be stored only once. Storing the data/information many times leads to the wastage of storage space and an increase in the total size of the data stored. Name Course Phone No Major Prof. Grade Vijay 160 2374539 Comp Sci V. Singh A Sanjay 170 4277390 Physics R. Singh B Vijay 165 2374539 Comp Sci S. Singh B Gopal 456 3885183 Mathematics R.J. Lal A Santosh 491 8237293 ·Chemistry Ved Prakash C Santosh 356 8237293 Chemistry J. Singh A Vijay 168 2374539 Comp Sci Vinay In prof. Updates to the database with such redundencies the potential of recoming inconsistent. In the above table the major and phone no. of a student are stored many times in the database. e.g., The major and phone no. of Vijay stored many times in the database. Thus it is the example of redundancy of data in the database. (2) Update Anomalies : Multiple copies of the same fact may lead to update anomalies or inconsistencies. When an update is made and only some of the multiple copies are updated. Thus, a change in the phone no. of 'Vijay' must be made for consistency, in all tuples pertaining to the student 'Vijay'. -

Identifying and Managing Technical Debt in Database Normalization Using Machine Learning and Trade-Off Analysis
Identifying and Managing Technical Debt in Database Normalization Using Machine Learning and Trade-off Analysis Mashel Albarak Muna Alrazgan Rami Bahsoon University of Birmingham UK King Saud University University of Birmingham King Saud University KSA KSA UK [email protected] [email protected] [email protected] ABSTRACT fast system release; savings in Person Months) and applying optimal design and development practices [21]. There has been Technical debt is a metaphor that describes the long-term effects an increasing volume of research in the area of technical debt. The of shortcuts taken in software development activities to achieve majority of the attempts have focused on code and architectural near-term goals. In this study, we explore a new context of level debts [21]. However, technical debt linked to database technical debt that relates to database normalization design normalization, has not been explored, which is the goal of this decisions. We posit that ill-normalized databases can have long- study. In our previous work [4], we defined database design debt term ramifications on data quality and maintainability costs over as: time, just like debts accumulate interest. Conversely, conventional ” The immature or suboptimal database design decisions database approaches would suggest normalizing weakly that lag behind the optimal/desirable ones, that manifest normalized tables; this can be a costly process in terms of effort themselves into future structural or behavioral and expertise it requires for large software systems. As studies problems, making changes inevitable and more have shown that the fourth normal form is often regarded as the expensive to carry out”. -

Database Normalization—Chapter Eight
DATABASE NORMALIZATION—CHAPTER EIGHT Introduction Definitions Normal Forms First Normal Form (1NF) Second Normal Form (2NF) Third Normal Form (3NF) Boyce-Codd Normal Form (BCNF) Fourth and Fifth Normal Form (4NF and 5NF) Introduction Normalization is a formal database design process for grouping attributes together in a data relation. Normalization takes a “micro” view of database design while entity-relationship modeling takes a “macro view.” Normalization validates and improves the logical design of a data model. Essentially, normalization removes redundancy in a data model so that table data are easier to modify and so that unnecessary duplication of data is prevented. Definitions To fully understand normalization, relational database terminology must be defined. An attribute is a characteristic of something—for example, hair colour or a social insurance number. A tuple (or row) represents an entity and is composed of a set of attributes that defines an entity, such as a student. An entity is a particular kind of thing, again such as student. A relation or table is defined as a set of tuples (or rows), such as students. All rows in a relation must be distinct, meaning that no two rows can have the same combination of values for all of their attributes. A set of relations or tables related to each other constitutes a database. Because no two rows in a relation are distinct, as they contain different sets of attribute values, a superkey is defined as the set of all attributes in a relation. A candidate key is a minimal superkey, a smaller group of attributes that still uniquely identifies each row. -

NEBC Database Course 2008 – Bonus Material
NEBC Database Course 2008 ± Bonus Material Part I, Database Normalization ªI once had a client ask me to normalize a database that already was. When I asked her what she was really asking for, she said, ©You know, so normal people can read it.© She wasn©t very techno-savvy.º Quetzzz on digg.com, 31st May 2008 In the course, we have shown how to design a well-structured database for your own use. The formal process of structuring your data in this way is known as normalization. Relational database theory, and the principles of normalisation, were first constructed by people with a strong mathematical background. They wrote about databases using terminology which was not easily understood outside those mathematical circles. Data normalisation is a set of rules and techniques concerned with: • Identifying relationships among attributes. • Combining attributes to form relations. • Combining relations to form a database. It follows a set of rules worked out by E F Codd in 1970. A normalised relational database provides several benefits: • Elimination of redundant data storage. • Close modelling of real world entities, processes, and their relationships. • Structuring of data so that the model is flexible. There are numerous steps in the normalisation process - 1st Normal Form (1NF), 2NF, 3NF, Boyce- Codd Normal Form (BCNF), 4NF, 5NF and DKNF. Database designers often find it unnecessary to go beyond 3rd Normal Form. This does not mean that those higher forms are unimportant, just that the circumstances for which they were designed often do not exist within a particular database. 1st Normal Form A table is in first normal form if all the key attributes have been defined and it contains no repeating groups. -

Introduction to Databases Presented by Yun Shen ([email protected]) Research Computing
Research Computing Introduction to Databases Presented by Yun Shen ([email protected]) Research Computing Introduction • What is Database • Key Concepts • Typical Applications and Demo • Lastest Trends Research Computing What is Database • Three levels to view: ▫ Level 1: literal meaning – the place where data is stored Database = Data + Base, the actual storage of all the information that are interested ▫ Level 2: Database Management System (DBMS) The software tool package that helps gatekeeper and manage data storage, access and maintenances. It can be either in personal usage scope (MS Access, SQLite) or enterprise level scope (Oracle, MySQL, MS SQL, etc). ▫ Level 3: Database Application All the possible applications built upon the data stored in databases (web site, BI application, ERP etc). Research Computing Examples at each level • Level 1: data collection text files in certain format: such as many bioinformatic databases the actual data files of databases that stored through certain DBMS, i.e. MySQL, SQL server, Oracle, Postgresql, etc. • Level 2: Database Management (DBMS) SQL Server, Oracle, MySQL, SQLite, MS Access, etc. • Level 3: Database Application Web/Mobile/Desktop standalone application - e-commerce, online banking, online registration, etc. Research Computing Examples at each level • Level 1: data collection text files in certain format: such as many bioinformatic databases the actual data files of databases that stored through certain DBMS, i.e. MySQL, SQL server, Oracle, Postgresql, etc. • Level 2: Database -

Chapter- 7 DATABASE NORMALIZATION Keys Types of Key
Chapter- 7 DATABASE NORMALIZATION Keys o Keys play an important role in the relational database. o It is used to uniquely identify any record or row of data from the table. It is also used to establish and identify relationships between tables. For example: In Student table, ID is used as a key because it is unique for each student. In PERSON table, passport_number, license_number, SSN are keys since they are unique for each person. Types of key: 1. Primary key o It is the first key which is used to identify one and only one instance of an entity uniquely. An entity can contain multiple keys as we saw in PERSON table. The key which is most suitable from those lists become a primary key. o In the EMPLOYEE table, ID can be primary key since it is unique for each employee. In the EMPLOYEE table, we can even select License_Number and Passport_Number as primary key since they are also unique. o For each entity, selection of the primary key is based on requirement and developers. 2. Candidate key o A candidate key is an attribute or set of an attribute which can uniquely identify a tuple. o The remaining attributes except for primary key are considered as a candidate key. The candidate keys are as strong as the primary key. For example: In the EMPLOYEE table, id is best suited for the primary key. Rest of the attributes like SSN, Passport_Number, and License_Number, etc. are considered as a candidate key. 3. Super Key Super key is a set of an attribute which can uniquely identify a tuple. -

P1 Sec 1.8.1) Database Management System(DBMS) with Majid Tahir
Computer Science 9608 P1 Sec 1.8.1) Database Management System(DBMS) with Majid Tahir Syllabus Content 1.8.1 Database Management Systems (DBMS) understanding the limitations of using a file-based approach for the storage and retrieval of data describe the features of a relational database & the limitations of a file-based approach show understanding of the features provided by a DBMS to address the issues of: o data management, including maintaining a data dictionary o data modeling o logical schema o data integrity o data security, including backup procedures and the use of access rights to individuals/groups of users show understanding of how software tools found within a DBMS are used in practice: o developer interface o query processor11 show that high-level languages provide accessing facilities for data stored in a Database 1.8.2 Relational database modeling show understanding of, and use, the terminology associated with a relational database model: entity, table, tuple, attribute, primary key, candidate key, foreign key, relationship, referential integrity, secondary key and indexing produce a relational design from a given description of a system use an entity-relationship diagram to document a database design show understanding of the normalisation process: First (1NF), Second (2NF) and Third Normal Form (3NF) explain why a given set of database tables are, or are not, in 3NF make the changes to a given set of tables which are not in 3NF to produce a solution in 3NF, and justify the changes made File-based Systems A flat file database is a type of database that stores data in a single table. -

Database Normalization
CPS352 Lecture - Database Normalization last revised March 6, 2017 Objectives: 1. To define the concepts “functional dependency” and “multivalued dependency” 2. To show how to find the closure of a set of FD’s and/or MVD’s 3. To define the various normal forms and show why each is valuable 4. To show how to normalize a design 5. To discuss the “universal relation” and “ER diagram” approaches to database design. Materials: 1. Projectable of first cut at library FDs 2. Projectable of Armstrong’s Axioms and additional rules of inference (from 5th ed slides) 3. Projectable of additional rules of inference (from 5th ed slide) 4. Projectable of algorithm for computing F+ from F (from 5th ed slides) 5. Projectables of ER examples on pp. 11-12 6. Projectable of algorithm for computing closure of an attribute (From 5th ed slides) 7. Projectable of 3NF algorithm (From 5th ed slides) 8. Projectable of BCNF algorithm (5th ed slide) 9. Projectable of rules of inference for FD’s and MVD’s (5th ed slide) CHECK Projectable of additional MVD Rules (5th ed slide) 10.Projectable of 4NF algorithm (5th ed slide) 11.Projectable of ER diagrams and relational scheme resulting from normalizing library database. I. Introduction A. We have already looked at some issues arising in connection with the design of relational databases. We now want to take the intuitive concepts and expand and formalize them. 1 B. We will base most of our examples in this series of lectures on a simplified library database similar to the one we used in our introduction to relational algebra and SQL lectures, with some modifications 1.